[CV] Motion(2) - Background Subtraction

Yeontachi·2025년 8월 27일

Computer Vision Note

목록 보기

45/47

Background Subtraction

비디오 영상에서 우리가 주로 관심을 가지는 것은 정적인 배경(Background)이 아니라, 움직이는 객체(foreground objects)이다. Background Subtraction은 이러한 배경과 객체를 분리해주는 핵심 기법이다. 기본 아이디어는 시간에 따라 거의 변하지 않는 부분은 배경으로 간주하고, 새로운 변화나 움직임이 나타나는 부분은 객체로 추출하는 것이다.

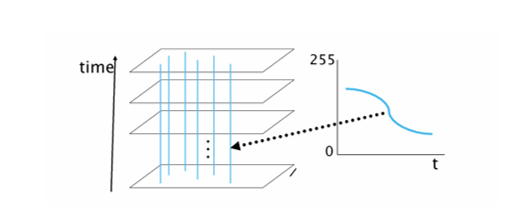
비디오를 시공간 데이터(spatiio-temporal volume)로 바라보면,

정적인 배경은 프레임이 변해도 거의 동일한 값을 유지한다. 움직이는 객체는 시간에 따라 픽셀 값이 변한다. 따라서 현재 프레임에서 배경 모델을 뺀 값이 임계값(threshold)을 넘으면 그 픽셀을 foreground로 판단한다.

Background Subtraction은 단순한 방법이지만, 다양한 응용에 활용된다.

교통 모니터링 : 차량 수 카운팅, 보행자 감지 및 추적
행동 인식(Human Action Recognition) : 걷기, 뛰기, 앉기 등의 동작 구분
인간-컴퓨터 상호작용(HCI) : 제스처 인식 등
객체 추적(Object Tracking) : 움직이는 객체의 궤적 추적

Pros and Cons

Pros

개념이 단순하고 구현이 쉽다.
정적인 카메라 환경에서는 효과적이다.
불필요한 배경 정보를 제거하므로 계산량이 줄어든다.

Cons

완벽히 구분하기 어렵다. 그림자, 조명 변화, 배경의 작은 움직임(예: 나무 흔들림) 때문에 오탐(false positive)이 발생할 수 있다.
움직이는 카메라에서는 적용하기 어렵다.

Background Subtraction의 여러 기법들

Simple Approach

기본 과정

(1) 배경 추정(Background Estimation) : 특정 시각 $t$ 에서의 배경 이미지를 $B(x,y,t)$ 라고 한다.

(2) Subtraction : 입력 영상 $I(x,y,t)$ 과 배경 $B(x,y,t)$ 의 차이를 계산한다.

D(x,y,t) = |I(x,y,t) - B(x,y,t)|

입력 영상: $I(x,y,t)$
배경 모델: $B(x,y,t)$

(3) 임계값 적용(Thresholding) : 차이가 임계값 $Th$ 를 넘는 픽셀을 foreground로 판단한다.

D(x,y,t) > Th\,\,\,\,\to\,\,\,\,\text{Foreground}

결과적으로 foreground mask를 얻을 수 있다.

핵심 문제는 배경 $B(x,y,t)$ 를 어떻게 추정할 것인가이다.

문제 해결 방안은, 단순히 이전 프레임을 배경으로 쓸 수도 있고(Frame Differencing),여러 프레임의 평균이나 중앙값을 이용할 수도 있다.(Mean/Median Filter)

더 발전된 방식으로는 Gaussian Mixture Model(GMM)같은 통계적 방법이나 최근에는 딥러닝 기반 기법도 사용된다.

Frame Differencing

이 방법은 배경을 직전 프레임으로 가정한다.

B(x,y,t) = I(x,y,t-1)

따라서 foreground 검출은:

|I(x,y,t) - I(x,y,t-1)| > Th

즉, 현재 프레임과 이전 프레임의 차이가 임계값을 넘으면 foreground로 판단한다.

아래 이미지는 Frame Differencing에서 임계값 $Th$ 값 변화에 따른 결과를 보여준다.

$Th = 25$ (작은 값) : 아주 작은 픽셀 차이도 foreground로 검출된다. 결과적으로 노이즈가 많고, 그림자나 미세한 움직임까지 객체로 잡힌다.

$Th=50$ (중간 값) : 불필요한 노이즈는 어느 정도 줄지만, 여전히 객체 외곽 부분이 많이 검출된다. 차량 같은 주요 객체는 잘 잡히지만, 일부 영역이 분리되지 않을 수 있다.

$Th = 100$ (큰 값) : 객체의 핵심 부분만 foreground로 남는다. 작은 움직임이나 객체 외곽은 사라진다. 결과적으로 foreground 객체의 형상이 불완전하다.

$Th = 200$ (아주 큰 값) : 대부분의 픽셀이 threshold를 넘지 못해 foreground가 거의 검출되지 않는다. 실제 움직임이 있어도 놓치게 되는 검출 실패 상황이 발생한다.

위 예시는 Frame Differencing이 얼마나 Threshold 값에 민감한 방법인지 보여준다.

그래서 실전에서는 단일 threshold 대신 적응형 thresholding이나 더 정교한 배경 모델링(Mean, Median, GMM)을 사용해 안정성을 높인다.

Mean Filter

배경을 이전 $n$ 프레임의 평균으로 추정한다.

B(x,y,t) = \frac{1}{n} \sum_{i=0}^{n-1} I(x,y,t-i)

따라서 foreground 검출은:

\Big| I(x,y,t) - \frac{1}{n} \sum_{i=0}^{n-1} I(x,y,t-i) \Big| > Th

즉, 최근 $n$ 개의 프레임을 보고 픽셀별 평균값을 배경으로 삼은 뒤, 현재 프레임과의 차이를 threshold로 판단하는 방식이다.

위 그림은 $n=10$ 일 때의 예시로,
Estimated Background : 최근 10프레임 평균으로 얻은 배경 영상
Foreground Mask : 평균과 차이를 낸 결과, 차량들이 foreground로 검출된다.

Mean Filter는 여러 프레임의 평균을 이용해 배경을 모델링하기 때문에 Frame Differencing보다 신뢰성이 높다. 하지만 움직임이 느리거나 멈춰 있는 객체는 결국 배경으로 흡수된다는 한계가 있다.

Median Filter

배경을 최근 $n$ 프레임의 픽셀 값 중앙값(median)으로 추정한다.

B(x,y,t) = median \{ I(x,y,t-i) \}, \quad i \in [0, n-1]

Foreground 검출은 다음과 같이 수행된다.

| I(x,y,t) - median\{ I(x,y,t-i) \} | > Th

즉, 과거 $n$ 개의 프레임을 모아 해당 픽셀의 중앙값을 배경으로 정하고, 현재 프레임과 비교한다.

위 그림은 $n=10$ 일 때의 예시로,
Estimated Background : 최근 10프레임 중앙값으로 얻은 배경 영상이다. 차량이 지나가도 대부분 지워진 깨끗한 도로만 남는다.

Foreground Mask : 현재 프레임에서 움직이는 차량이 foreground로 검출됨을 확인할 수 있다.

Median Filter는 Mean Filter보다 일시적인 움직임에 강하다. 예를 들어, 어떤 사람이 잠깐 서 있었다가 사라지면 평균에는 잔상이 남지만, 중앙값은 일시적 변화에 잘 영향을 받지 않는다. 또한 더 안정적인 배경 모델을 제공하며, 그림자나 일시적 물체 출현(ghosting 효과)을 줄인다.

하지만, Mean Filter보다 계산량이 많으며, 객체가 오랫동안 같은 위치에 있으면, 중앙값에도 포함되어 결국 배경으로 흡수된다.

정리하면, Median Filter는 여러 프레임의 중앙값을 사용해 배경을 추정하므로, 일시적 움직임이나 노이즈에 강하고, 평균 기반보다 더 깨끗한 배경 모델을 얻을 수 있다. 그 덕분에 차량 검출, 보행자 추적 등에서 안정적인 성능을 보여준다.

왼쪽은 평균 영상이다. 광장에 있던 사람들이 아직 남아있는 모습을 볼 수 있다.