[CV] Digital Image Fundamentals : Warping

Yeontachi·2025년 7월 30일

AI Computer_Vision

Computer Vision Note

목록 보기

4/47

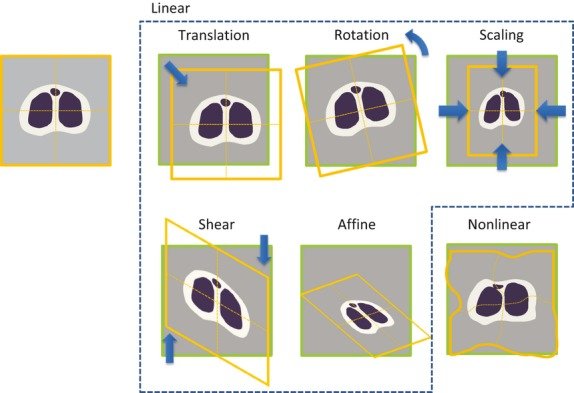
Warping?

Warping은 이미지를 다른 좌표계로 변환하는 작업을 의미한다. 쉽게 말해, 픽셀의 위치를 재배치해서 이미지의 형태를 바꾸는 과정이다.

예를 들어,

사진을 회전할 때 → 픽셀 좌표가 바뀜
이미지를 확대/축소할 때 → 좌표를 다시 계산
종이 사진을 카메라로 비스듬히 찍었을 때 → 이를 펴는 작업(Perspective Warping)

이들 모두 Warping에 속한다.

모든 Warping은 결국 좌표 변환이다.

(x', y') = T(x, y)

여기서:

$(x, y)$ : 원본 이미지의 픽셀 좌표
$(x', y')$ : 변환 후 이미지의 픽셀 좌표
$T$ : 변환을 정의하는 수학적 함수(행렬 or 비선형 함수)

주요 Warping 유형 정리

(1) Translation(이동)

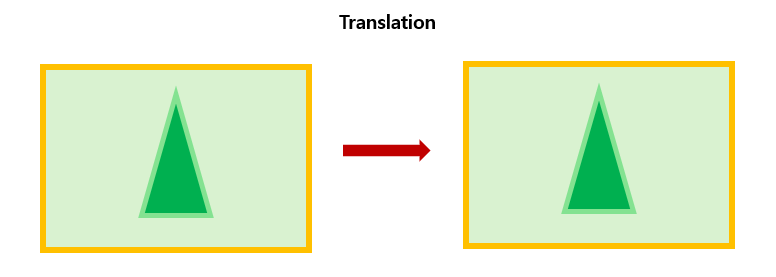
이미지를 단순히 좌우, 위아래로 움직이는 변환이다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix}

$t_x$ : x 방향 이동 거리
$t_y$ : y 방향 이동 거리

(2) Scalling (확대/축소)

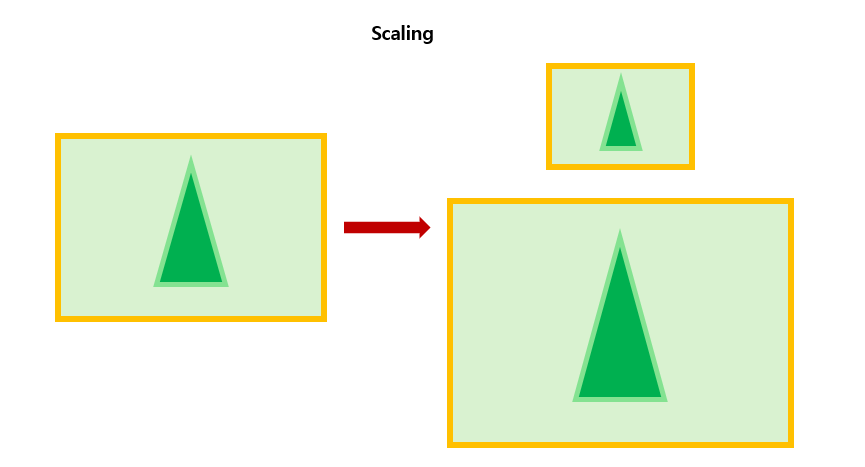
이미지를 크게하거나 작게 만드는 변환이다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

$s_x$ : x축 스케일 비율
$s_y$ : y축 스케일 비율

(3) Rotation (회전)

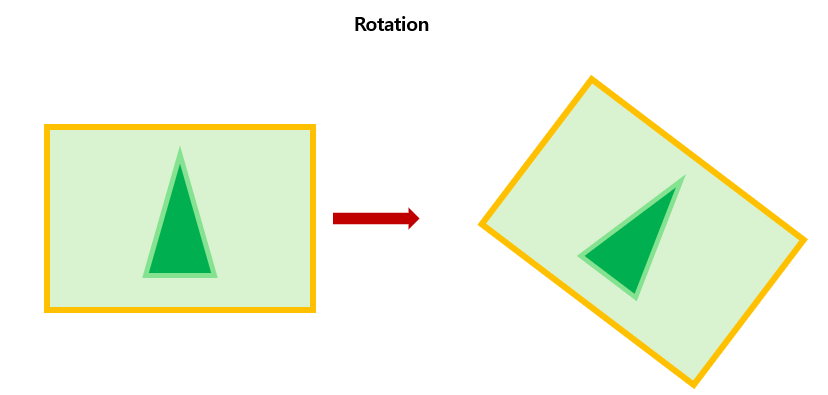
이미지를 원점을 기준으로 회전시키는 변환이다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

$\theta$ : 회전 각도(라디안 단위)

(4) Shearing (기울이기)

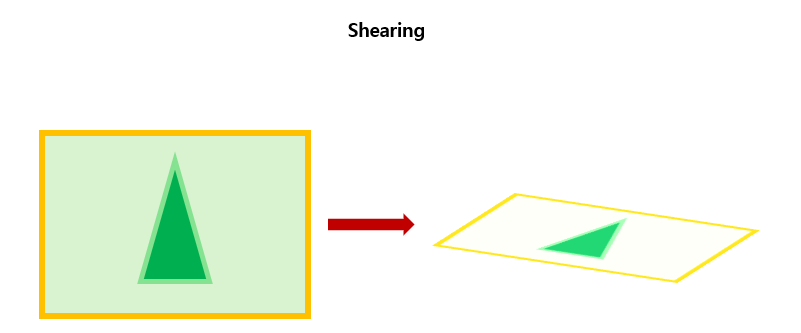
이미지를 기울이는 변환이다.

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & sh_x \\ sh_y & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}

$sh_x$ : x축 방향 기울기
$sh_y$ : y축 방향 기울기

(5) Affine Transformation

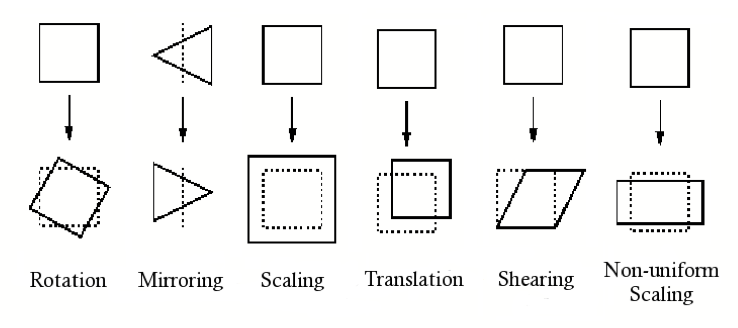
Affine 변환은 평행성을 유지하는 모든 선형 변환이다.(이동, 회전, 스케일, 쉬어 모두 포함)

\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & t_x \\ a_{21} & a_{22} & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

Affine 변환은 최소 3쌍의 대응점이 필요하다.

(6) Perpective Transformation

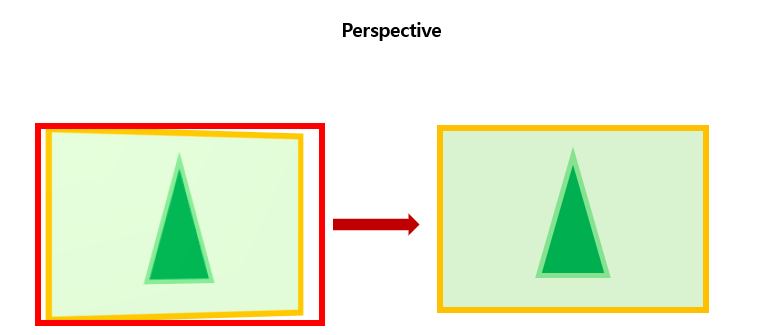
Perpective(투시) 변환은 카메라로 사진을 비스듬히 찍은 이미지를 정면으로 보정하는 데 사용된다. 이 변환은 직선은 유지하지만, 평행선은 소실점으로 수렴할 수 있다.

\begin{bmatrix} x' \\ y' \\ w \end{bmatrix} = \begin{bmatrix} p_{11} & p_{12} & p_{13} \\ p_{21} & p_{22} & p_{23} \\ p_{31} & p_{32} & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}

최종 좌표:

x'' = \frac{x'}{w}, \quad y'' = \frac{y'}{w}

정리

변환	특징
Translation	위치만 이동
Scaling	확대/축소
Rotation	회전
Shearing	기울이기
Affine	평행성 유지, 6자유도 변환
Perspective	투시 변환, 소실점 표현 가능

Yeontachi

기초를 다지는 중입니다.📚🧑‍💻

이전 포스트

[CV] Digital Image Fundamentals : Image Zoom & Interpolation

다음 포스트