디지털 영상처리는 단순히 이미지를 다루는 것처럼 보이지만, 본질적으로는 신호 처리(Signal Processing)의 연장선에 있다. 우리가 흔히 보는 이미지는 공간 좌표(x, y)에 따라 밝기 값이 변하는 2차원 신호이고, 영상에서 시간 축까지 포함하면 3차원 신호(비디오)가 된다. 따라서 이미지를 분석하고 변환하기 위해서는 신호의 특성과 이를 다루는 신호 처리 기법을 이해하는 것이 매우 중요하다.
왜 신호 처리가 필요한가?
- 이미지는 데이터 그 자체가 아니라 정보의 집합이다.
우리가 보고 싶은 것은 단순한 픽셀 값이 아니라, 그 안에 숨어 있는 특징(feature)과 패턴(pattern)이다. 예를 들어, 이미지에서 물체의 모서리(Edge)나 텍스처(Texture)를 찾으려면, 단순한 밝기 값만 보는 것으로는 부족하다. 여기서 신호 처리 개념이 필요하다. - 잡음 제거, 선명화, 복원, 압축과 같은 작업은 모두 신호 처리를 기반으로 한다.
예를 들어, 사진이 흐릿할 때 선명하게 만드는 과정(샤프닝)은 신호에서 고주파(high frequency) 성분을 강조하는 작업이다. 반대로 잡음을 줄이는 과정(스무딩)은 저주파(low frequency) 성분을 강화하는 방식이다. - 공간(domain)과 주파수(domain) 이해의 필요성
영상은 공간 도메인(Spatial Domain)에서 보면 픽셀들의 배열이지만, 주파수 도메인(Frequency Domain)으로 변환하면 이미지의 패턴을 주파수 성분으로 해석할 수 있다. 예를 들어,- 평탄한 영역(하늘, 벽) → 저주파 성분 위주
- 경계나 세부 구조(텍스처, 엣지) → 고주파 성분 위주
신호 처리 기본 개념
연속 신호 vs 이산 신호
연속 신호(Continuous-Time Signal) : 시간 또는 공간 좌표가 연속적인 값을 가지는 신호이다.
실제 아날로그 음성, 자연 영상 등이며, 모든 시간(또는 공간) 지점에 대해 값이 정의된다. 디지털 카메라의 광센서에서 받아들인 빛은 연속 신호로 시작한다.
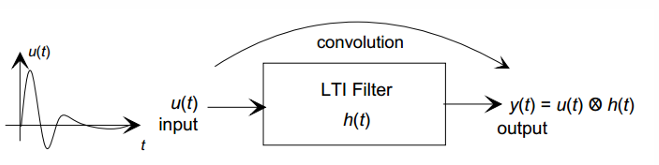
여기서, 연속적인 파형 에 대한 신호 처리는 연속 LTI(Linear Time-Invariant) 시스템을 이용해 수행된다.

이산 신호(Descrete-Time Signal) : 연속 신호를 특정 간격으로 샘플링하여 얻은 신호이다.
디지털 영상은 2차원 이산 신호의 대표적인 예이다.
실제 이미지:
이산 신호를 사용하는 이유
현실의 신호는 연속적이지만, 디지털 처리를 위해서는 컴퓨터가 다룰 수 있는 형태(샘플 값)로 변환해야 한다. 이 과정이 샘플링(Sampling)이며, 디지털 이미지는 결국 이산 2D 신호의 집합이다.
이산 신호 처리는 디지털 영역에서 샘플링된 데이터를 기반으로 컴퓨터 알고리즘, 합산 기반 처리를 한다.
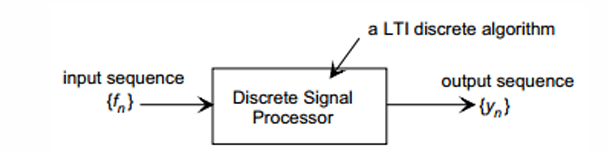
Digital Signal Processors
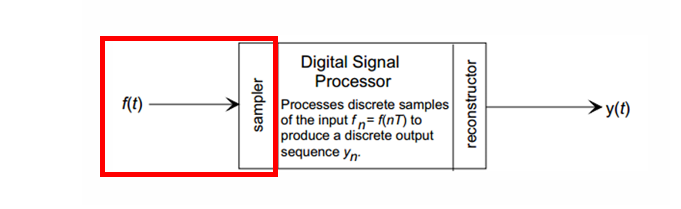
는 아날로그 형태의 연속 신호(Continuous-Time Signal)이다. Sampler는 연속 신호 를 **일정한 시간 간격 로 측정해 이산 신호 로 변환한다.(Sampling)
이때, 나이퀴스트(Nyquist) 정리에 따라, 원본 신호를 잃지 않으려면(: 초당 샘플링 횟수)
원 신호의 최대 주파수의 2배 이상으로 샘플링해야 한다.

샘플링된 데이터는 이제 이산 신호이므로 컴퓨터나 DSP 칩(Digital Signal Processor)에서 처리할 수 있다. 이 단계에서 다양한 연산이 가능하다.
- 오디오 : 잡음 제거, 이퀄라이저, 압축
- 영상 : 블러링, 샤프닝, 경계 검출, 객체 인식
출력은 여전히 이산 형태의 데이터, 즉 이산 출력 시퀀스 이다.
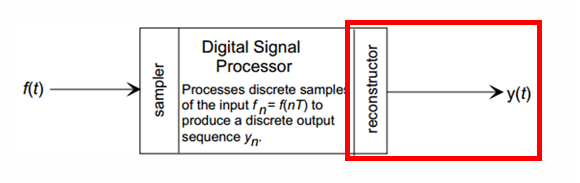
필요한 경우, DAC(Digital-to-Analog Converter)를 이용해 디지털 처리 후 결과를 다시 연속 신호로 변환한다.
예를 들면,
- 스피커에서 소리를 내기 위해 디지털 오디오 → 아날로그 전압 변환
- 모니터 화면에 빛으로 표시하기 위해 디지털 영상 → 광신호 변환
이 과정을 통해 최종 연속 출력 가 생성된다.
흐름 요약
LTI(Linear Time-Invariant System)
LTI 시스템은 선형(linear)이고 시불변(Time-Invariant)한 시스템을 의미한다. 디지털 영상처리, 오디오 처리 등 대부분의 신호 처리 기법에서 핵심적인 역할을 한다.
(1) 선형성(Linearity)
입력이 선형 결합이면 출력도 선형 결합이다.
즉, 두 입력 에 대해:
필터에 두 신호를 더해서 넣은 결과는, 두 신호를 각각 처리한 뒤 더한 것과 동일하다.
(2) 시불변성(Time-Invariance)
입력이 시간에 따라 이동하면, 출력도 동일하게 이동한다.
시스템이 어떤 시점에서 작동해도 동작 방식이 변하지 않는다. 예를 들면, 오늘 적용한 블러 필터는 내일도 똑같이 작동한다.
LTI 시스템의 3가지 중요한 특성
(a) 중첩의 원리(The Principle of Superposition)
선형 시스템에서는 여러 입력의 선형 결합에 대한 응답은 각 입력의 응답을 같은 비율로 결합한 것과 같다.
입력 에 대한 출력이 각각 라면, 의 출력은 이다.
예를 들면, 영상에서 두 이미지를 합성한 뒤 필터를 적용하는 것과 각 이미지에 필터를 적용 후 합치는 것은 동일하다.
(b) 미분 특성(Differentiation Property)
입력 신호가 원래 신호의 미분이라면, 출력은 원래 출력의 미분이다.
미분 연산이 시스템 출력에도 그대로 적용된다. 예를 들면, 경계 검출에서 1차 미분 필터(Sobel, Prewitt)는 이 개념을 기반으로 한다.
(c) 적분 특성(Integration Property)
입력이 원래 신호의 적분이라면, 출력은 원래 출력의 적분이다.
적분 연산 역시 LTI 시스템과 교환 가능하다. 예를 들면, 누적 합 연산이 가능하다는 의미이다.
Continuous LTI System Time-Domain Response
- 입력: (연속 신호)
- 시스템: LTI 필터
- 목표 : 출력 는 어떻게 구할 것인가?
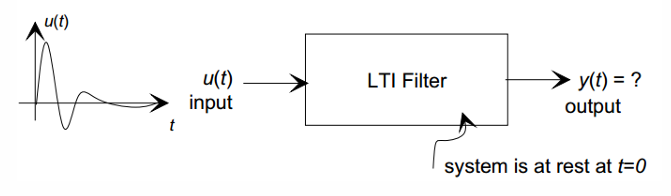
입력 → LTI 시스템 → 출력
시스템은 =0에서 rest 상태이다. 즉, 이전 입력의 영향은 없고 현재 입력만 고려한다.
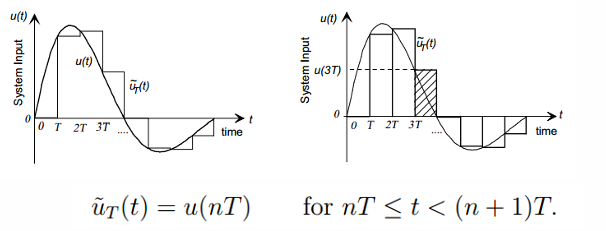
원래 연속 신호 를 일정한 간격 로 잘라서, 각 구간에서 상수값으로 표현한다. 이렇게 근사된 신호를 라고 한다.
각 구간의 값 를 이용해 구간별 사각형 pulse를 만들고, 이 pulse를 LTI 시스템에 넣으면 개별 응답이 생긴다.
이때 최종 출력은 이 개별 Response들의 합으로 결정된다.
즉, n번째 구간에서 입력은 로 고정된다.
요약하자면,복잡한 연속 신호가 작은 사각형 pulse 합으로 근사되고, 각 pulse에 대한 시스템 응답을 계산 후 합쳐서 최종 출력 를 생성한다.
위 단계를 좀 더 수학적으로 표현하면,
신호 근사(Superposition)
여기서,
즉, 원래 신호를 일정 구간 로 잘라서 pulse들의 합으로 표현한다.
Pulse 응답
각 pulse는 시스템에 입력될 때 임펄스 응답의 이동 버전으로 출력된다.
즉, n번째 pulse → 시스템 응답이 만큼 지연되어 나타난다.
응답 합성
모든 pulse에 대한 응답을 더하면 아래와 같다.
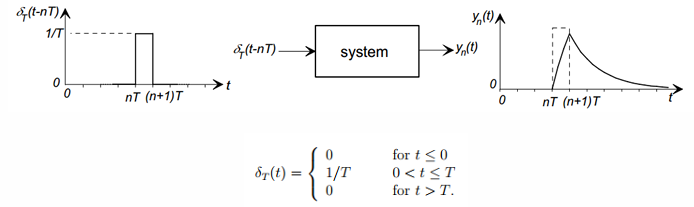
는 정규화된 pulse를 의미하며, 높이는 이다. 각 pulse가 LTI 시스템을 통과하면 임펄스 응답 형태로 변환된다. 결과는 이후 감소하는 형태이다.
System Response
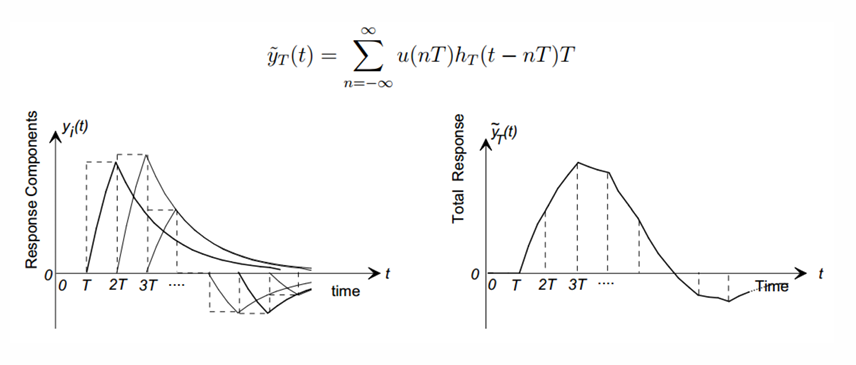
입력 를 샘플링하고, 각 샘플 값 에 대응하는 시스템 응답을 합산하여 근사 출력 를 계산한다.
왼쪽 그래프는 라는 샘플 값에 대해 LTI 시스템이 생성하는 응답들이고, 이 응답들이 합쳐져 오른쪽 그래프, 합산된 총 응답 이 출력된다.
Total Response의 형태는 처음에는 입력이 들어오면서 점차 커지고, 여러 응답이 겹치며 중간에 최대값에 도달한다. 이후 입력이 없으므로 시스템 특성(감쇠)에 따라 서서히 감소한다.
특징으로는 입력 신호의 부호 변화가 응답에 반영되엉 부호 변화 구간이 존재하며, 결국 LTI 필터 특성(예: 저역 통과)이 반영된 형태로 부드러운 곡선이 형성된다.
pulse 근사에서 (샘플 폭)를 매우 작게 만들면 신호는 거의 연속처럼 표현이 가능하다.
이때, (폭이 T인 pulse)는 T→0일 때 Dirac delta 함수 로 수렴한다.
위 아이디어로, 합에서 적분으로 변환을 하면,
임펄스 응답 는
즉, T→0일 때 시스템 응답을 나타내는 함수가 임펄스 응답이다.
최종 결과: Convolution Integral
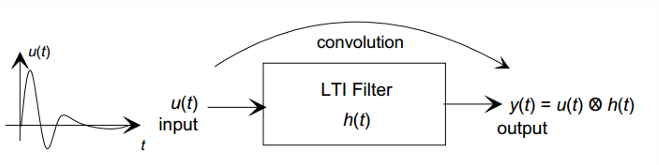
즉, 정리를 하면 LTI 필터는 입력 신호를 임펄스 응답으로 변형하는 장치이다. 임펄스 응답 는 "시스템이 단위 임펄스(함수)를 받았을 때 어떻게 반응하는가"를 나타낸다.
따라서, 입력을 임펄스의 집합으로 생각하면, 각 임펄스에 대한 응답을 구하고 선형 시스템이므로 응답을 모두 더하면 최종 출력이 된다. 이것이 컨볼루션이다.
Convolution (컨볼루션)
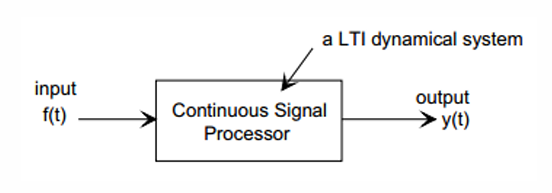
입력: 연속 신호
Continuous Signal Processor
- LTI 시스템을 나타낸다. 시스템의 특성은 임펄스 응답 로 완전히 정의된다. 즉 "이 시스템이 단위 임펄스()에 어떻게 반응하는가"가 인 것이다.
출력:
- 입력 신호가 시스템을 통과했을 때의 결과로, LTI 시스템에서는 출력이 입력과 시스템의 임펄스 응답의 컨볼루션으로 표현된다.
컨볼루션은 위에서 정리한 식으로 정의된다.
즉, 입력 신호의 각 순간 값이 시스템에 어떻게 영향을 미치는지 누적한 결과이다.
대부분의 영상처리에서 블러, 샤프닝, 잡음 제거 등 대부분의 연산이 컨볼루션 연산으로 모델링 되어 있다.
