[CV] Feature Detection and Matching(2) - Feature Point Detection, Harris Corner

영상에서 특징점을 검출하는 것은 컴퓨터 비전의 핵심 과제 중 하나이다. 단순히 모든 픽셀을 비교하는 대신, 우리는 작고 안정적인 지역(local) 특징을 추출하여 이미지 매칭, 모자이크 생성, 3D 재구성, 객체 인식 등 다양한 응용에 활용한다.

특징점(Feature Point)는 크게 코너(corner), 에지(edge), 블롭(blob)과 같이 주변 대비가 뚜렷하고 반복적으로 검출 가능한 지점으로 정의된다. 이 중에서도 코너(corner)는 두 방향으로 강항 밝기 변화가 발생하는 영역을 의미하며, 다른 영역에 비해 재현성(repeatability)과 구별성(distinctiveness)이 뛰어나기 때문에 안정적인 매칭에 매우 유용하다.

1988년 Harris와 Stephens가 제안한 Harris Corner Detector는 이러한 특징점 검출의 대표적인 알고리즘으로, 지역 윈도우(Window) 안에서의 강도 변화(Intensity variation)를 수학적으로 모델링하여 코너를 찾는다. Harris 방법은 단순히 기울기(edge)만 보는 것이 아니라, 창(window)을 작은 방향으로 이동했을 때 얼마나 큰 강도 변화가 발생하는가를 분석한다. 만약 모든 방향으로 큰 변화가 나타난다면, 그 지점은 코너로 판단된다.

이 접근은 단순하면서도 강력하여, 잡음에 대한 강인성, 회전 불변성(rotation invariance)을 제공하며, 현재까지도 다양한 컴퓨터 비전 파이프라인의 기본 빌딩 블록으로 활용되고 있다. 특히 SIFT나 SURF와 같은 현대적 로컬 특징 기술자(local feature descriptor)의 설계 역시 Harris와 같은 초기 코너 검출기에서 출발하였다.

Corners as Distinctive Interest Points

특징점을 찾을 때 가장 중요한 기준 중 하나는, 윈도우(window)를 어느 방향으로 이동시켰을 때 강도(Intensity)가 크기 변하는가이다. Harris 검출기는 이 개념을 수학적으로 모델링하여, 평탄한 영역(flat), 에지(edge), 코너(corner)를 구별한다.

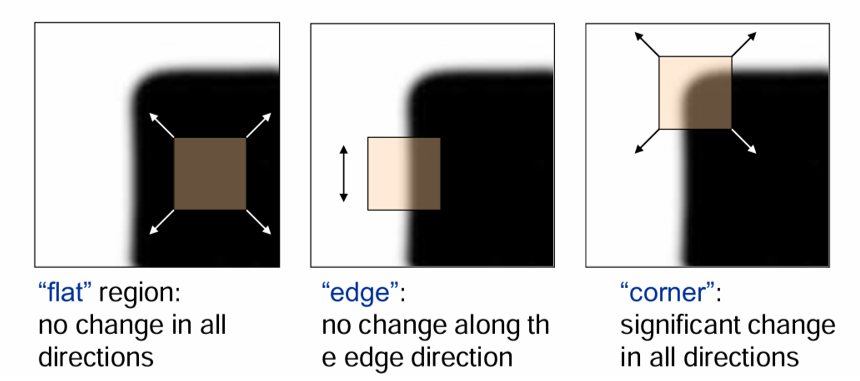
• Flat region(평탄 영역)
  왼쪽 그림처럼, 전체가 비슷한 밝기를 가진 균일한 영역에서는 윈도우를 어느 방향으로 움직여도 강도의 변화가 거의 없다. 따라서 Flat 영역은 특징점으로 적합하지 않다.

  $$

• Edge(에지 영역)
  가운데 그림처럼, 에지 방향으로 이동하면 변화가 거의 없지만, 에지 방향과 수직으로 이동하면 강한 강도 변화가 발생한다.
  즉, 한 방향에서는 구별성이 있지만 다른 방향에서는 안정적인 특징이 되지 못한다.

• Corner(코너 영역)
  오른쪽 그림처럼, 코너 부분에 위치한 윈도우는 어떤 방향으로 움직이더라도 강한 강도 변화를 일으킨다.
  이는 구별성(Distinctiveness)이 높다는 의미이며, 매우 안정적인 특징점으로 사용될 수 있다.

Corners versus Edges

특징점 검출에서 중요한 것은 픽셀 밝기 강도 변화율(gradient)이다.

이를 위해 이미지 밝기 함수를 $I(x,y)$라 할 때,

• $I_x = \frac{\partial I}{\partial x}$ : x 방향 기울기
• $I_y = \frac{\partial I}{\partial y}$ : y 방향 기울기

를 구한다. 이 값들의 제곱을 지역(window) 내에서 합산하면, 해당 영역이 flat, edge, corenr 중 어디에 속하는지를 판단할 수 있다.

1. Corner(코너)

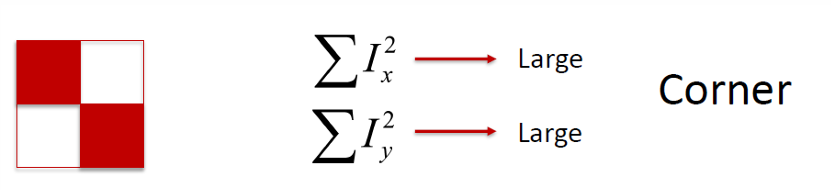
x, y 방향 모두 강한 변화가 존재한다.
즉, 어떤 방향으로 이동해도 강도의 변화가 크므로 구별 가능한 지점이다.

2. Edge(에지)

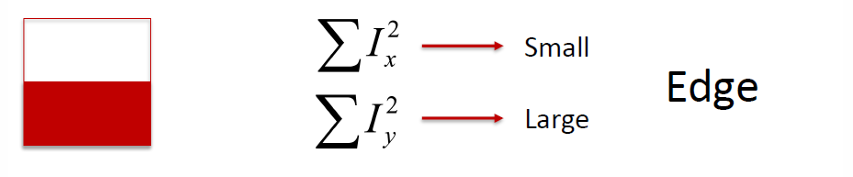
(반대로 x는 크고 y는 작을 수 있음)

한 방향(에지에 수직한 방향)으로는 강한 변화가 있지만, 에지를 따라 움직이는 방향에서는 변화가 없다. 따라서 모호성이 존재해 좋은 특징점이 되지 못한다.

3. Flat region(Nothing, 평탄 영역)

모든 방향에서 강도 변화가 거의 없다.
즉, 균일한 영역이라서 매칭에 사용할 정보가 없다.

Measure change in all directions

코너를 검출하기 위해서는 윈도우(window)를 여러 방향으로 조금씩 이동시켰을 때, 강도 변화량을 측정해야 한다.

• 이미지 강도 함수: $I(x,y)$
• 이동 벡터: $[u, v]$
• 이동 후 위치의 강도: $I(x+u, y+v)$

따라서 한 점의 강도 변화는 다음과 같이 표현된다.

즉, 윈도우를 이동시켰을 때 원래 위치와의차이를 측정하는 것이다.

윈도우 누적

하지만 단일 픽셀만 비교하는 것은 잡음이나 지역적 변화에 취약하다.
그래서 실제 Harris 알고리즘에서는, 하나의 픽셀이 아니라 작은 윈도우(Window) 안의 모든 픽셀에 대해 변화량을 합산한다.

즉,

• $w(x,y)$ : 윈도우 함수(가우시안 가중치 등)
• 합산을 통해 주변 영역까지 고려 $\to$ 잡음에 강건(robust)

각 영역별 $E(u,v)$ 값을 살펴보면 아래와 같다.

• Flat 영역 : 모든 방향으로 이동해도 변화 거의 없음 $\to$ $E(u,v)$ 작음
• Edge 영역 : 특정 방향으로만 큰 변화, 다른 방향은 거의 없음 $\to$ $E(u,v)$ 한쪽만 큼
• Corner 영역 : 어떤 방향으로 이동해도 큰 변화 $\to$ $E(u,v)$ 모든 방향에서 큼

Harris Detector Fomulation

코너를 검출하기 위해서는 작은 윈도우를 다양한 방향으로 이동시켰을 때 밝기(Intensity)가 얼마나 변하는지를 측정해야 한다.

1. 변화량 측정 함수

윈도우를 $[u,v]$만큼 이동시켰을 때의 변화량은 다음과 같이 정의된다.

• $w(x,y)$ : 윈도우 함수(예: 사각형 윈도우, Gaussian 가중치)
  

• $I(x+u, y+v)$ : 이동된 윈도우의 픽셀 강도

• $I(x,y)$ : 원래 윈도우의 픽셀 강도

즉, 윈도우를 이동했을 때 밝기 차이를 제곱함으로 측정하는 방식이다.

2. 테일러 전개(근사)

함수 $I(x+u, y+v)$를 1차 테일러 전개하면,

여기서 $I_x,I_y$는 각각 x, y 방향에 대한 밝기 변화율(미분, gradient)이다.

이를 대입하면,

3. 두 번째 모멘트 행렬(Structure Tensor)

여기서 $M$은 다음과 같은 $2\times 2$ 행렬이다.

• $I_x, I_y$ : 각 픽셀의 기울기(gradient)

• 이 행렬은 해당 영역(Window)에서의 방향별 변화율을 요약한다.

• 따라서 $M$의 고유값(eigenvalue)을 보면, 변화가 없는 평탄한 영역인지, 한 반향으로만 변하는 에지인지, 모든 방향에서 변하는 코너인지를 구분할 수 있다.

  

$I_x$는 x방향(좌우 방향)의 밝기 변화를 계산하므로, 세로 경계선이 밝게 강조된 이미지가 만들어진다.

$I_y$는 y방향(위아래)의 밝기 변화를 계산하므로, 가로 경계선이 밝게 강조된 이미지가 만들어진다.

$I_xI_y$의 경우 x,y가 동시에 변화하는 코너 영역에서 강하게 나타난다.

즉, 수식과 함께 직관적으로 보면,
Flat 영역에서는 $I_x, I_y$ 모두 작으므로 $M$의 값이 작다.
Edge 영역에서는 x또는 y 중 한 방향 미분만 크므로, $M$이 한 축으로만 커진다.
Corner 영역에서는 두 방향 모두 크므로 $M$의 두 고유값 모두 크다.

행렬 M의 의미를 좀 더 자세히 살펴봐보면,

위 $2\times 2$ 행렬은 해당 영역에서의 기울기(gradient) 분포를 요약해준다. 즉, 이 행렬을 보면 "이 윈도우 안에서 픽셀이 어느 방향으로 많이 변하는가?"를 알 수 있다.

행렬 $M$의 고유값 $λ_1,λ_2$의 의미는 다음과 같다.

• $λ_1$: 한 축(주된 방향)으로의 기울기 크기

• $λ_2$: 그에 직교하는 축으로의 기울기 크기

  

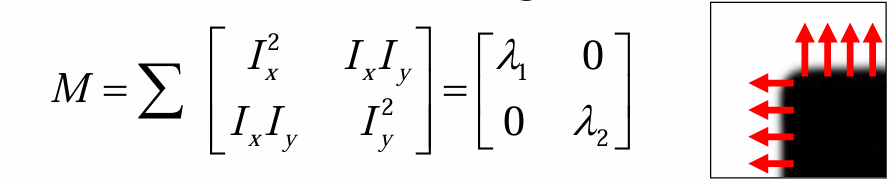
위 우측 그림처럼, 모서리가 x축, y축 방향으로 정렬되어있다고 가정해보면, 행렬 $M$은 위 수식처럼 대각행렬로 단순화된다.

즉, $λ_1$이 크다는 뜻은 x축 방향(좌우)으로 강한 변화가 있다는 의미이고, $λ_2$ 크다는 것은 y축 방향(상하)으로 강한 변화가 있다는 의미이다. 즉, 두 방향 모두 큰 값이면 "코너"임을 의미한다.

하지만, 실제 영상에서의 코너는 축 방향으로 정렬된 형태가 아닌 코너가 임의의 방향으로 기울어진 케이스가 일반적이다.

$M$은 항상 대칭(symmetric) 행렬이다. 따라서 고유값 분해(Eigenvalue Decomposition)가 가능하다.

여기서 $\lambda_1, \lambda_2$는 고유값, $R$은 회전(고유벡터 방향)을 나타낸다.

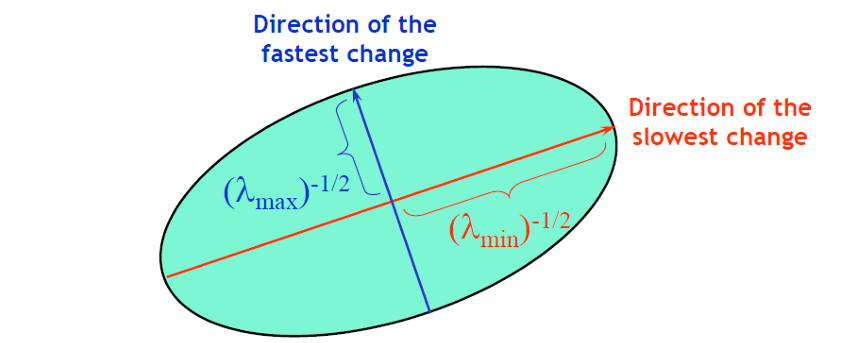
행렬 $M$은 해당 영역의 강도 변화(gradient distribution)를 타원으로 표현할 수 있다.

이때 타원의 축 길이는 고유값에 의해 결정된다.

• 긴 축 = $(\lambda_{\min})^{-1/2}$
• 짧은 축 = $(\lambda_{\max})^{-1/2}$
  타원의 방향은 고유벡터 $R$이 결정한다.

즉, $\lambda_{\max}$ 의 크기는 가장 빠른 변화 방향(Gradient가 큰 방향, $\lambda_{\min}$ 의 크기는 가장 느린 변화 방향을 나타낸다.

강도 변화 측면에서 살펴보면, 위의 두 고유값이 모두 크면, 모든 방향에서 강한 변화가 나타났단 의미로, 코너 영역임을 의미하며, 한쪽만 큰 경우는 엣지 영역, 둘 다 작은 경우는 평탄 영역임을 의미한다.

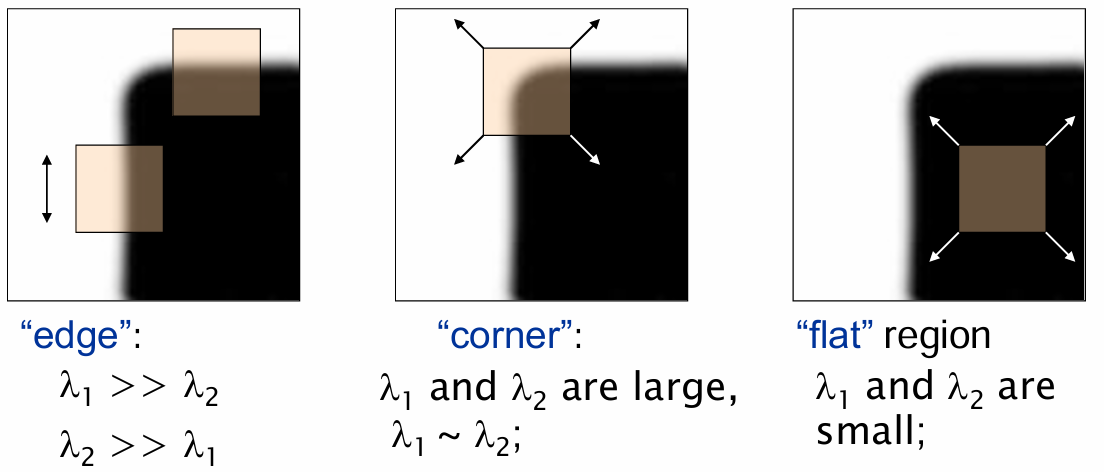
정리하면 이 위 타원은 해당 픽셀 주변의 밝기 변화가 어느 방향으로 강한지를 시각화한 도구이고, $\lambda$ 값들이 코너/에지/평탄 영역을 구분하는 핵심 지표가 된다.

Eigenvalues Interpretation 고유값을 통한 영상 영역 분류

영상의 특정 지점에서 계산된 행렬 $M$의 고유값 $\lambda_1, \lambda_2$는 그 지점 주변의 강도 변화(gradient) 특성을 나타낸다. 이를 통해 해당 지점이 평탄 영역(Flat), 에지(Edge), 코너(Corner) 중 어디에 속하는지를 판별할 수 있다.

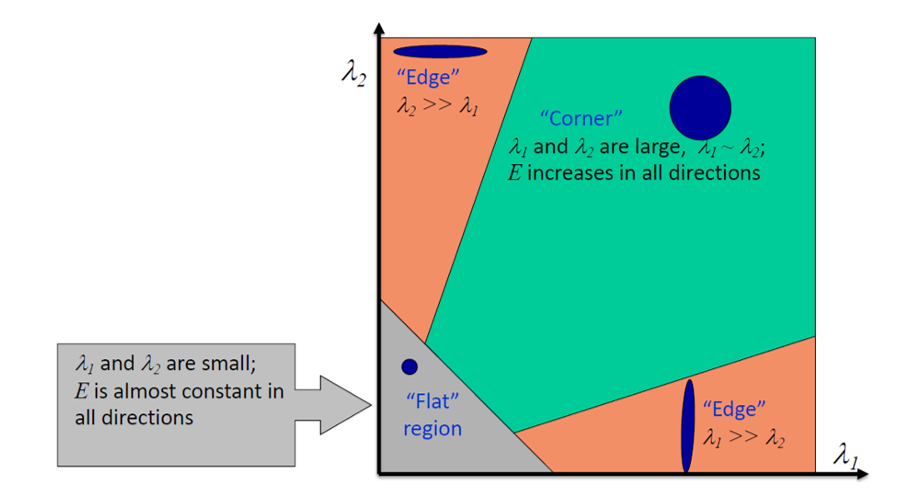
1. Flat region
$\lambda_1$과 $\lambda_2$가 모두 작은 경우, 영상의 강도 변화가 거의 없다. 즉, 모든 방향에서 밝기가 일정하여 특징점이 될 만한 요소가 없다. 예를 들어, 흰 종이 위 아무 무늬 없는 부분이 이에 해당한다.

2. Edge region
한쪽 고유값은 크고 다른 하나는 작은 경우, 영상의 밝기 변화가 특정 방향으로만 강하게 나타난다.
예를 들어, 세로 방향으로 밝기 변화가 크면 가로 방향의 에지가 나타난다.
이때는 점보다 선의 형태가 강조되며, 코너보다는 덜 구별되는 특징점이다.

3. Corner region
$\lambda_1$과 $\lambda_2$가 모두 크고, 그 크기도 서로 비슷한 경우이다. 이는 두 방향 모두에서 밝기 변화가 크다는 의미이며, 교차점이나 모서리와 같이 주변 구조가 뚜렷하게 드러나는 지점을 나타낸다.
따라서 코너는 영상에서 가장 안정적이고 구별 가능한 특징점으로 활용된다.

Corner Response Function

앞서 본 것처럼 고유값 $\lambda_1, \lambda_2$는 코너 여부를 판별하는 데 중요한 기준이 된다. 하지만 실제 계산에서 고유값을 직접 구하는 것은 연산량이 크다. 이를 효율적으로 계산하기 위해 Harris 코너 검출기에서는 다음과 같은 Corner Response Funtion을 사용한다.

• $\det(M) = \lambda_1\lambda_2$
• $trace(M) = \lambda_1 + \lambda_2$
• $\alpha$ : 경험적으로 정한 상수(보통 0.04 ~ 0.06)

1. 코너 영역(Corner, $\theta > 0$)

• $\lambda_1, \lambda_2$가 모두 크고 비슷한 경우, 즉 모든 방향에서 강한 밝기 변화가 존재한다. 이때 $\det(M)$이 커지고 $\theta>0$이 되어 코너로 분류된다.

2. 에지 영역(Edge, $\theta < 0$$)

• 한쪽 고유값은 크지만 다른 하나가 매우 작은 경우,
  $det(M)$ 값은 작아지고 $trace(M)^2$이 크게 작용하여 $\theta<0$이 된다.
  따라서 이 지점은 에지로 분류된다.

3. 평탄 영역(Flat, $\theta ≈ 0$)

• $\lambda_1, \lambda_2$ 모두 작은 경우,
  $det(M)$과 $trace(M)$ 모두 작아져서 $\theta$도 0에 가깝게 된다.
  이때는 변화가 거의 없는 평탄 영역으로 분류된다.

Harris 응답 함수는 고유값을 직접 구하지 않고도 코너 여부를 빠르게 판별할 수 있다.

실제 영상 처리에서 효율적으로 코너를 검출할 수 있어, 다양한 컴퓨터 비전 응용(특징점 추출, 이미지 해석 등)에 활용된다.

Haris Detector Responses

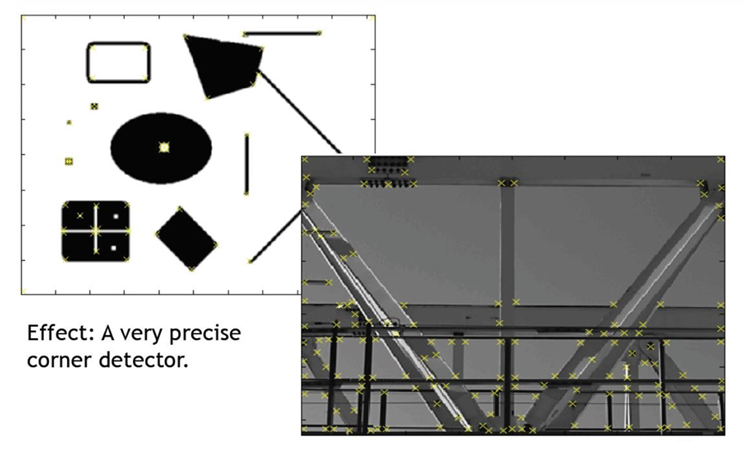
아래 그림은 Harris Detector가 실제로 어떻게 코너 포인트를 응답(responses)하는지 보여준다.

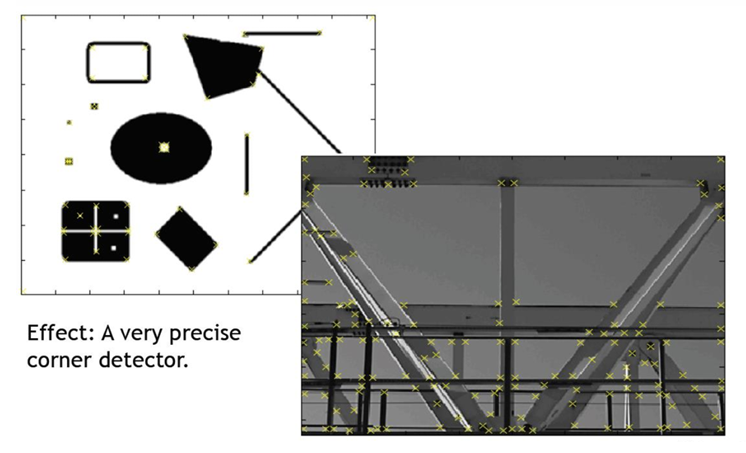
왼쪽 그림을 보면, 도형의 모서리 부분, 사각형의 네 귀퉁이, 교차점 등에서 정확히 코너가 잡혀 있다. 즉, Harris Detector가 단순 도형의 구조적 특징을 잘 포착한다는 의미이다.

우측 그림을 보면, 마찬가지로 교차지점, 난간의 모서리, 구조물의 꺾이는 부분 등에 코너 포인트가 표시되어 있다.
배경의 균일한 영역에서는 코너가 거의 검출되지 않고, 구조적 변화가 있는 지점에만 응답한다.

결과적을, 도형 영상에서느느 이상적인 모서리만 잡히고, 실제 영상에서도 구조적 특징점이 안정적으로 추출되는 것을 확인할 수 있다.

Harris Detectors Step

아래 이미지를 이용해 Harris 코너 검출 과정을 살펴봐보자.

1. Corner Response $f$ 계산

아래 그림은 입력 영상에 대해 corner response $f$ 값을 계산한 결과를 보여준다.

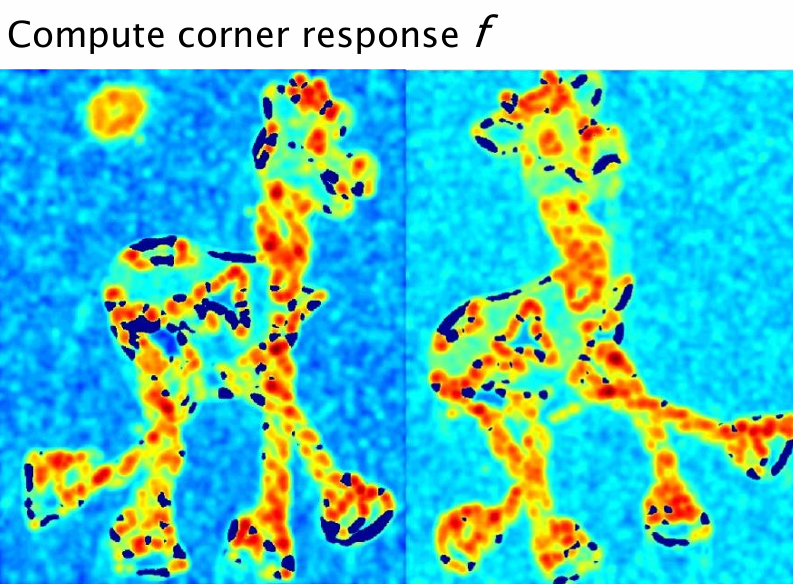
• 파란색 영역은 $f$값이 낮아 코너가 아닌 부분이다.
• 빨간/노란 영역은 $f$ 값이 크며, 코너일 가능성이 높은 부분을 나타낸다.
  즉, 영상 내 모든 픽셀에 대해 코너 가능성을 수치화한 결과이다.

2. Threshold 적용

아래 이미지는 일정 기준(threshold) 이상의 $f$ 값을 가진 픽셀만 잠정적인 코너 후보로 남겨둔다.

• 흰색 점들은 $f > \text{threshold}$를 만족하는 위치이다.
• 검은색 영역은 무시된 부분이다.
  이를 통해 불필요한 잡음을 제거하고 후보점을 줄일 수 있다.

3. Non-maximum Suppression 지역 극대값

다음 그림은 threshold로 남은 후보점들 중에서 지역적으로 가장 큰 응답값을 갖는 점만 선택한 결과이다.

• 이렇게 해야 코너가 밀집된 영역에서 불필요하게 많은 포인트가 검출되지 않고, 진짜 코너 포인트만 남게 된다.

4. 최종 코너 검출 결과

다음 그림은 원본 이미지 위에 최종 코너 포인트들을 표시한 결과이다.

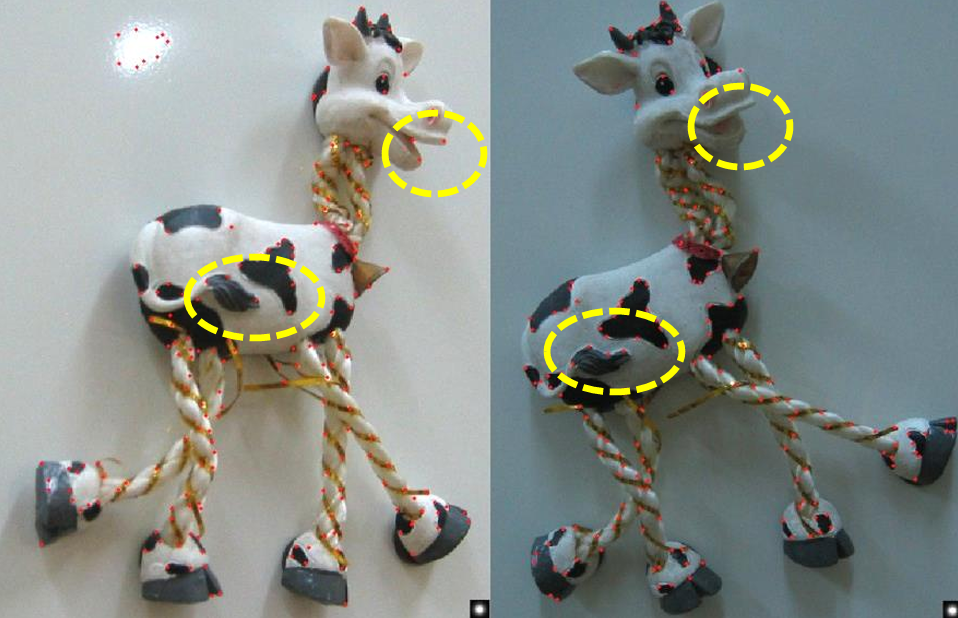
• 빨간 점들이 Harris Detector가 선택한 코너들이다.
• 노란색 원으로 강조된 부분은 코너가 특히 잘 잡힌 부분이다.

Properties of Harris Corner Detector

Harris 코너 검출기는 영상에서 코너를 잘 찾아내는 강력한 기법이지만, 그 특성을 살펴보면 다음과 같은 불변성(Invariance) 측면에서 장단점이 존재한다.

1. Translation Invariance 이동 불변성
영상 전체가 평행 이동하더라도, 픽셀 강도의 상대적인 변화는 그대로 유지된다. 따라서 Harris 코너 검출기의 응답은 이동에 영향을 받지 않는다. 즉, Translation invariant하다.

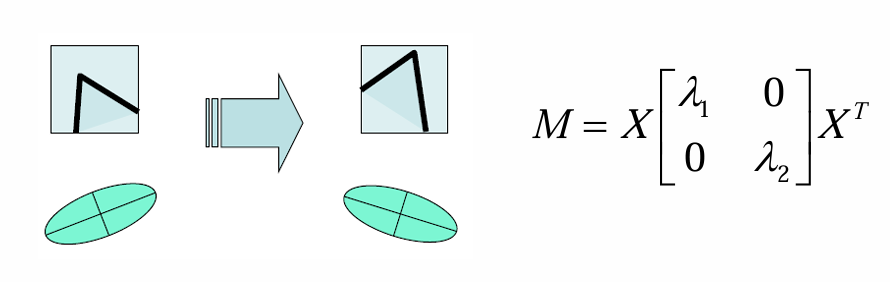
2. Rotation Invariance 회전 불변성
Harris 검출 구조 텐서(Matrix M)의 고유값($\lambda_1, \lambda_2$)을 이용한다. 회전이 발생하면 좌표계는 변하지만 고유값 자체는 회전 불변적인 특성을 가진다. 따라서 코너 여부는 동일하게 판단된다. 즉, Rotation invariant하다.

3. Scale Invariance 크기 불변성
문제는 스케일 변화이다.
윈도우 크기가 고정된 상태에서 영상이 확대되면, 코너가 더 큰 구조로 바뀌게 되어 국소 윈도우 안에서는 더 이상 코너로 보이지 않는다. 이 경우 Harris 검출기는 코너를 엣지(Edge)로 잘못 분류할 수 있다.

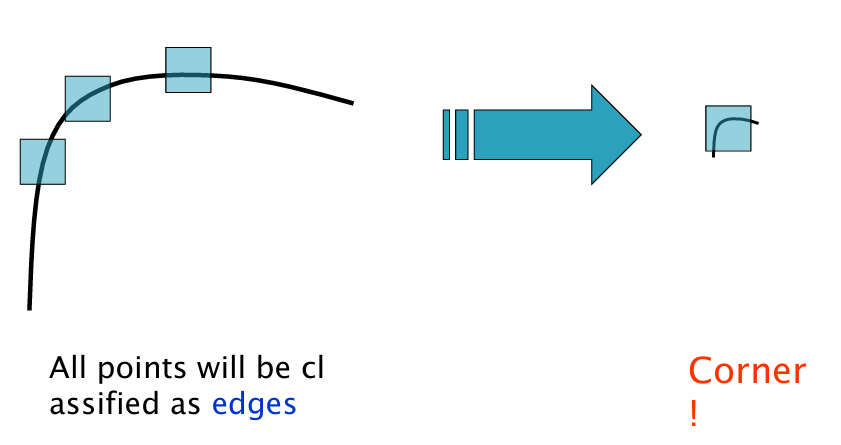
즉, Harris 코너 검출기는 Scale invariant하지 않다.

이 한계 때문에 이후에 등장한 SIFT(Scale-Invariant Feature Transform)와 같은 알고리즘에서는 스케일 공간(scale space)을 고려하여 멀티스케일 코너 검출을 수행한다.

References

Computer Vision: Algorithms and Applications 2nd Edition - Richard Szeliski

Digital Image Processing 2nd Rafael C.Gonzalez, Richard E. Woods