[CV] Feature Detection and Matching(3) - Scale Invariant Keypoint Detection

Yeontachi·2025년 8월 20일

Computer Vision Note

목록 보기

29/47

영상 혹의 특징점(feature point)을 검출하는 과정에서 가장 큰 도전 중 하나는 스케일(scale) 변화에 대한 불변성을 확보하는 것이다. 즉, 객체가 크거나 작아지더라도 동일한 특징점이 안정적으로 검출되어야 한다. Harris Corner Detector와 같은 전통적인 방법은 이동(translation)과 회전(rotation)에 대해서는 강건(robust)하지만, 스케일 변화에는 취약하다. 이를 극복하기 위해 자동 스케일 선택(Automatic Scale Selection) 개념이 도입되었다.

스케일 불변성을 갖기 위해서는 우선 좋은 함수(good function)이 필요하다. 이 함수는 스케일 변화에도 동일한 응답을 유지하며, 특정 위치와 슼케일에서 최대값(극값)을 갖도록 설계되어야 한다. 대표적인 예로 블롭 검출(Blob Detection)이 있으며, 이는 영상 내 밝기 변화가 둥근 영역을 이루는 패턴을 찾아내는 방법이다. 2차원 영상에서 블롭을 검출하기 위해 LoG(Laplacian of Gaussian)이나 DoG(Difference of Gaussian) 필터가 사용된다.

이러한 블롭 검출 과정은 단일 스케일에서 끝나는 것이 아니라, 스케일 공간(Scale-space)으로 확장된다. 스케일 공간에서는 영상이 다양한 크기의 가우시안 필터로 연속적으로 스무딩 처리되며, 각 스케일에서의 응답을 분석함으로써 스케일 불변 관심점(scale-invariant interest points)을 검출할 수 있다. 이는 객체가 확대되거나 축소되더라도 동일한 지점이 선택되도록 보장한다.

기술적으로, 스케일 공간 블롭 검출기(scale-space blob detector)는 영상의 각 지점과 스케일에서 Laplacian 응답을 계산하고, 그 결과에서 극대점을 찾아 특징점을 정의한다. 이 과정에서 계산 효율성을 위해 DoG가 자주 활용된다.

마지막으로 검출된 특징점은 단순히 위치만 필요한 것이 아니라, 이후 매칭을 위해 기술자(descriptor)로 표현된다. 기술자는 특징점 주변의 패턴을 스케일 $\cdot$ 회전에 강인하게 요약하여, 다른 영상 간에 동일한 특징점을 안정적으로 대응시킬 수 있도록 한다. 대표적으로 SIFT와 SURF가 이러한 접근을 구현한 알고리즘이다.

즉, Scale Invariant Keypoint Detection은 영상 크기가 달라져도 일관된 특징점을 검출하기 위해 자동 스케일 선택과 스케일 공간 분석을 활용하며, Blob Detection과 Descriptor 설계를 통해 불변성과 매칭 가능성을 확보하는 과정이다.

Automatic Scale Selection

스케일 불변 특징점을 검출하기 위해서는 단순히 위치에서의 극대값만 찾는 것이 아니라, 스케일 차원에서도 극대값을 찾는 과정이 필요하다. 즉, 어떤 특징점이 다양한 크기(스케일)에서 관찰되더라도 안정적으로 동일한 점을 특징으로 인식할 수 있어야 한다. 이를 위해 사용되는 개념이 Automatic Scale Selection이다.

How do we find corresponding patch sizes?

객체가 두 영상에서 서로 다른 크기로 나타나더라도, 동일한 지점을 특징점으로 검출하려면 적절한 패치 크기(윈도우 크기)를 찾아야 한다.

작은 패치 크기는 세밀한 구조를 잡을 수 있지만 큰 스케일 변화에는 약하다.

큰 패치 크기는 잡음에는 강하지만 작은 구조를 놓칠 수 있다.

따라서 스케일 변화에 변화하는 함수 $f(x,y, \sigma)$ 를 정의하고, 그 함수가 위치 (x, y)와 스케일 $\sigma$ 에서 동시에 국소 최대값(local minima)을 가지는 지점을 선택한다.

이렇게 선택된 스케일은 그 점을 설명하기에 가장 적절한 크기를 나타내며 이 과정을 통해 스케일 불변성을 달성한다.

Intuition

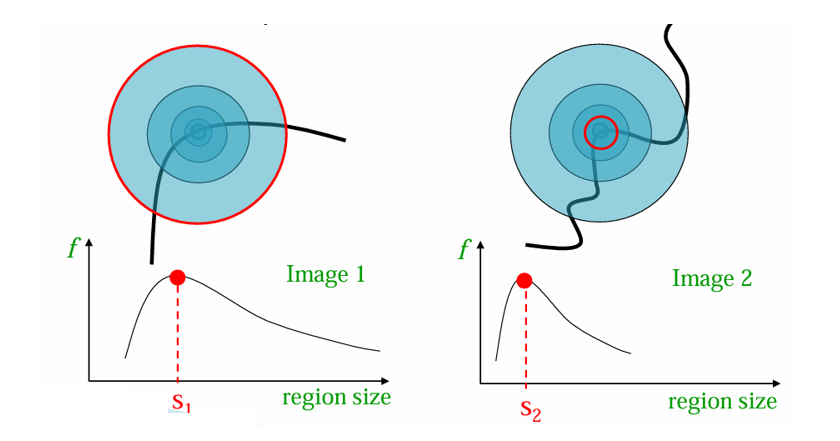
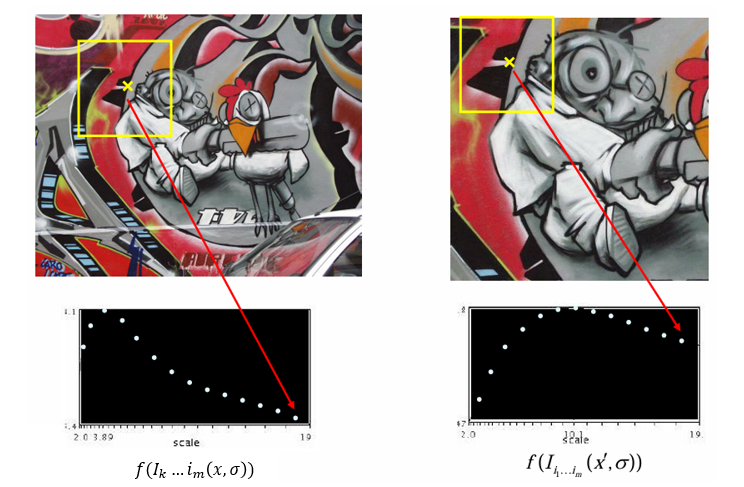
어떤 코너가, 큰 이미지(왼쪽)에서는 큰 영역을 잡았을 때 극대값을 주고, 축소된 이미지(오른쪽)에서는 작은 영역을 잡았을 때 극대값을 준다.

따라서 서로 다른 해상도나 크기의 이미지에서도 동일한 특징점이 검출되며, 이는 스케일 불변성을 보장한다.

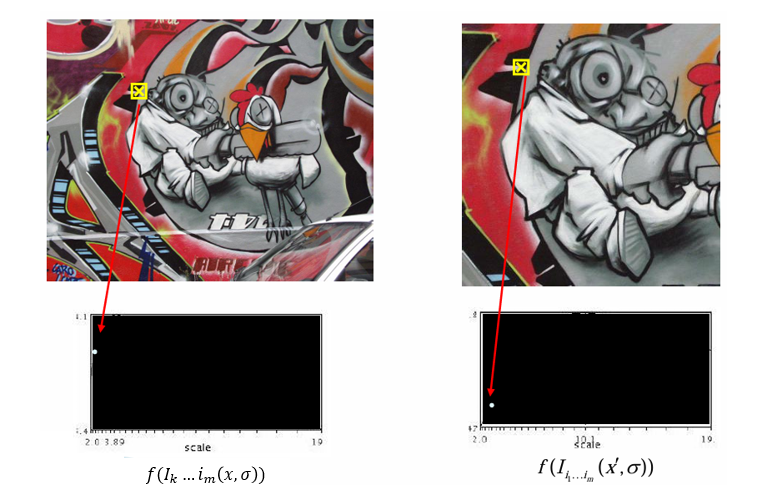
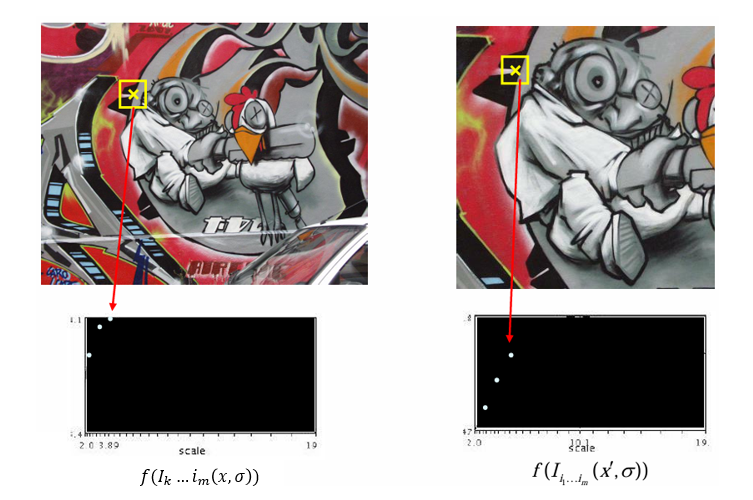
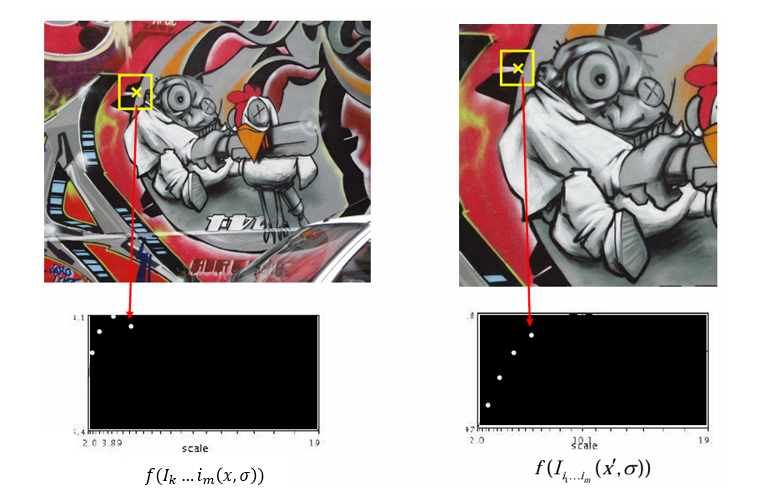
아래 이미지들은, 이미지 특징이 가장 잘 드러나는 스케일 함수 $f(x, \sigma)$ 의 지역 최대값을 통해 자동으로 찾아내는 과정이다.

즉, 이미지 내의 특정 특징점(예: 모서리, 블롭 등)이 어떤 스케일에서 가장 쭈렷하게 나타나는지를 찾는 과정이다.

Good function for scale detection

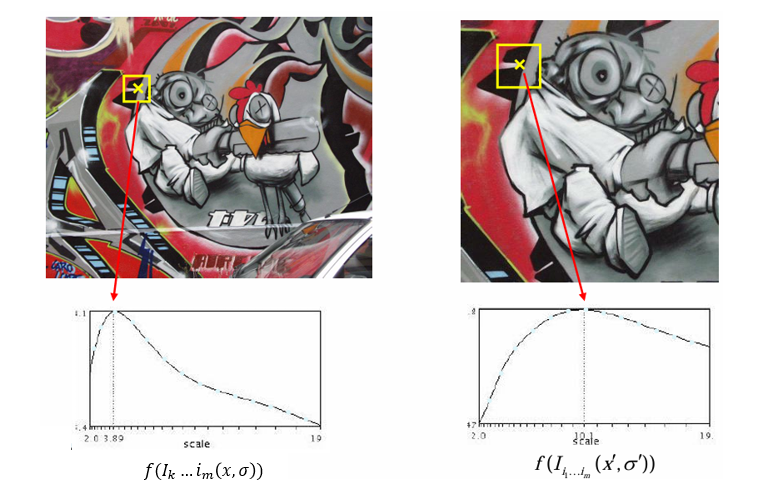
스케일 불변 검출을 위해서는, 스케일을 변화시키면서 함수 $f(x, \sigma)$ 의 값을 관찰할 때, 하나의 뚜렷하고 안정적인 피크(peak)가 존재해야 한다.

너무 평평한 함수의 경우 여러 스케일에서 값이 거의 비슷하다. 즉, 어떤 스케일이 최적인지 판단하기 어렵다.

여러 개의 극대를 갖는 경우, 여러 스케일에서 반응이 강해, 어느 스케일을 선택해야 할지 애매해 진다.

명확하게 한 번만 튀어나오는 Sharp peak의 경우, 이 피크 위치( $\sigma$ 값)가 "좋은 스케일"로 선택된다.

즉, 좋은 함수는 스케일 공간에서 안정적이고 유일한 극대값을 주며, 이는 이미지에서 의미 있는 특징점을 잘 포착하게 해준다.

Blob Detection in 2D

Blob이란, 이미지에서 균일하게 밝거나 어두운 영역으로, 주변과 강하게 대비되는 덩어리 같은 구조를 말한다.

예를 들어, 동그란 점, 구멍, 물체의 내부 영역 등이 Blob에 해당한다.

즉, Blob Detection은 점(spot), 원, 타원 같은 덩이리 구조를 찾는 과정이다.

Laplacian of Gaussian (LoG)

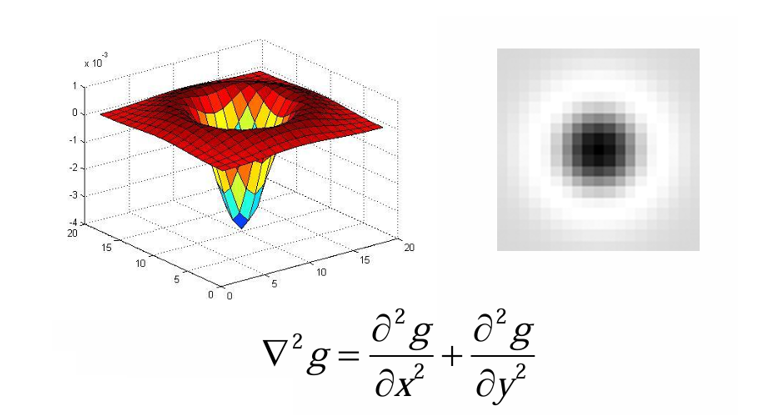
Laplacian of Gaussian(LoG)는 가우시안 스무딩(노이즈 억제)과 Laplacian(2차 미분, 밝기 변화 강조)을 결합한 연산자이다.

Laplacian은 2차 미분으로, x축, y축 방향을 구분하지 않고 모든 방향에서 동일하게 반응한다.

따라서 Blob처럼 원형 구조(동그란 점, 구멍 등)에 대해 방향에 관계없이 동일한 강도의 반응을 준다.

이 성질 덕분에 LoG는 Blob detection에 최적화된 연산자롸 불린다.

LoG : Scale Selection

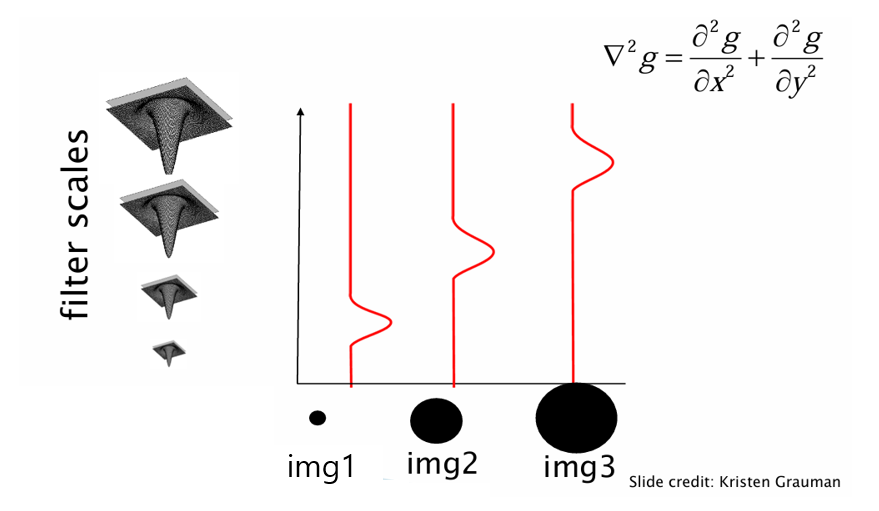
위 그림을 보면 알 수 있듯이, Blob의 크기와 LoG 응답의 스케일은 일치한다.

따라서 스케일 공간(Scale Space)에서 LoG의 응답이 최대가 되는 $\sigma$ 를 찾으면, 그 Blob의 크기를 추정할 수 있다.
( $\sigma$ 는 가우시간 필터의 표준 편차를 의미하고 이는 필터의 크기, 즉 관찰하는 스케일을 결정한다.)

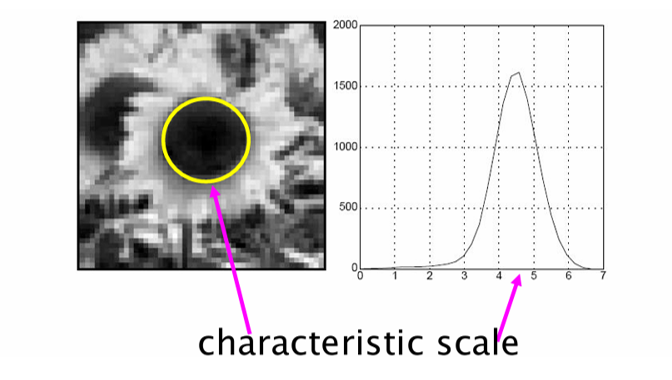
왼쪽 그림의 원형 Blob이 있고, 다양한 크기의 필터로 스캔했을 때, Blob 크기와 잘 맞는 스케일에서 응답이 가장 강하게 나온다.

오른쪽 그래프의 x축은 스케일( $\sigma$ ), y축은 LoG 응답 크기이다.

$\sigma$ 가 작을 때는 Blob 크기에 비해 필터가 작아서 응답이 약하다.
$\sigma$ 가 너무 크면 Bloob이 희석되어 응답이 다시 줄어든다.
중간의 peak(≈ σ=4~5)가 Blob의 실제 크기에 해당한다.

정리하면, Characteristic scale = LoG 응답이 가장 강한 스케일 즉, 이 값이 Blob의 크기를 대표하는 척도이다.

Scale Invariant Interest Points

스케일 불변 특징점(Scale Invariant Interest Points)이란 영상에서 크기(Scale)가 달라지더라도 안정적으로 검출되는 점을 의미한다. 예를 들어 같은 물체가 더 가까이 다가오거나 멀어져 보이는 경우에도, 동일한 위치를 특징점으로 검출할 수 있어야 한다.

이러한 특징점을 찾기 위해서는 두 가지 조건을 만족해야 한다.

1. 위치에서의 극대값(Local Maxima in Position)

영상 내 특정 좌표 (x, y)에서 필터 응답이 뚜렷한 최대값을 가져야 한다. 이는 에지나 코너처럼 지역적으로 두드러진 특징을 의미한다.

2. 스케일에서의 극대값(Local Maxima in Scale)

특정 크기 $\sigma$ 에서 응답이 가장 크게 나타나야 한다. 이는 해당 특징이 특정 스케일(예: 블롭의 크기)에 잘 맞음을 의미한다.

따라서 특징점은 단순히 한 위치에서만 찾는 것이 아니라, **위치(x,y)와 스케일 $\sigma$ 의 3차원 공간에서 극대값을 갖는 점으로 정의된다.

Example
원본 해바라기 사진에서 여러 크기의 해바라기 들이 존재한다. 이때, LoG 기반의 필터를 다양한 $\sigma$ 로 적용하여, 여러 스케일에서 반응을 측정한다.

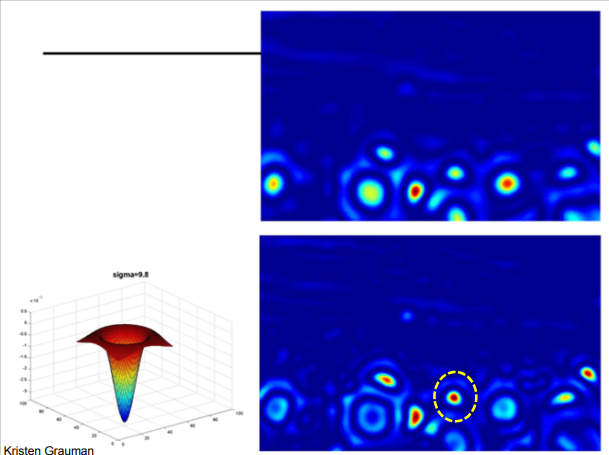
아래 이미지는 $\sigma = 2.1$ 로, 작은 해바라기의 중심에서 강한 응답이 나타난다.(작은 블롭 검출)

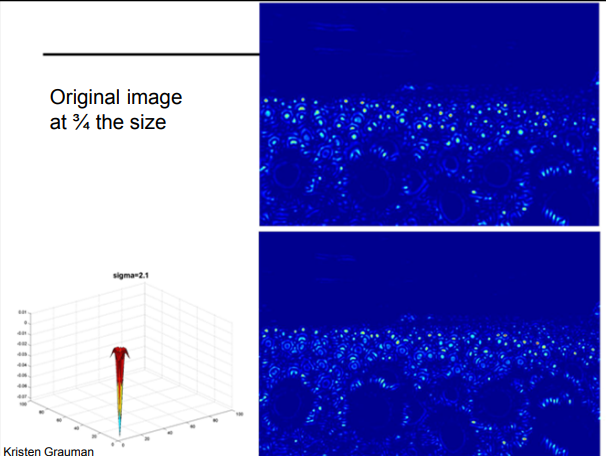
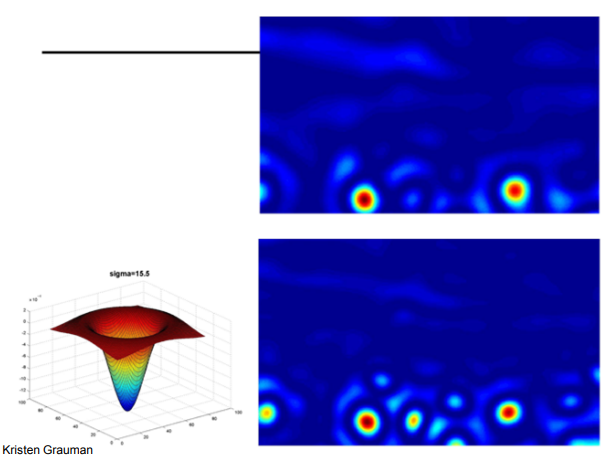
$\sigma = 4.2, 6$ 의 경우 중간 크기의 해바라기가 뚜렷하게 나타난다.

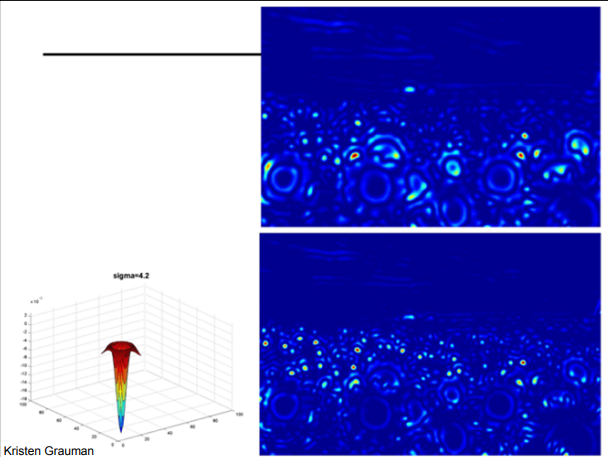
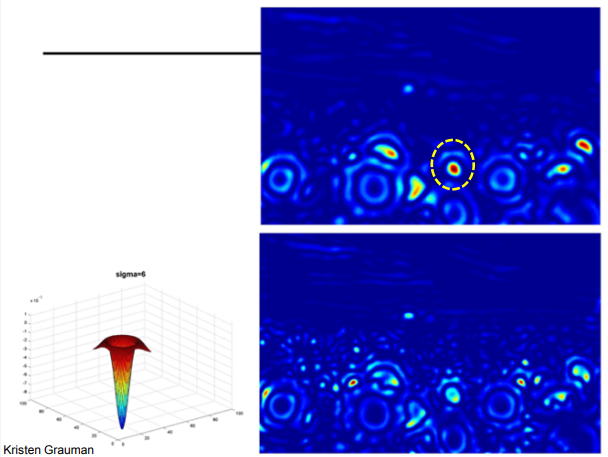
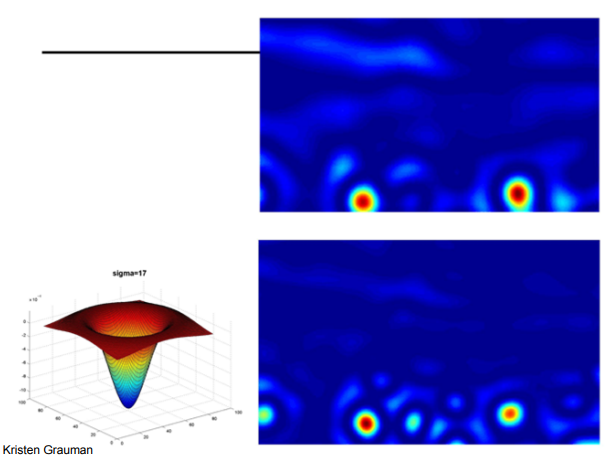
$\sigma = 9.8, 15.5, 17$ 의 경우 큰 해바라기가 최대로 응답되어 큰 블롭이 검출된다.

즉, 정리하면
특징점 = 위치(x,y) + 스케일 $\sigma$ 에서의 극대값이며,

단순한 좌표가 아니라 크기까지 포함된 **3차원 특징 벡터(x, y, $\sigma$ )로 표현된다.

이를 통해 영상이 확대/축소되더라도 동일한 해바라기를 같은 특징점으로 매칭할 수 있다.

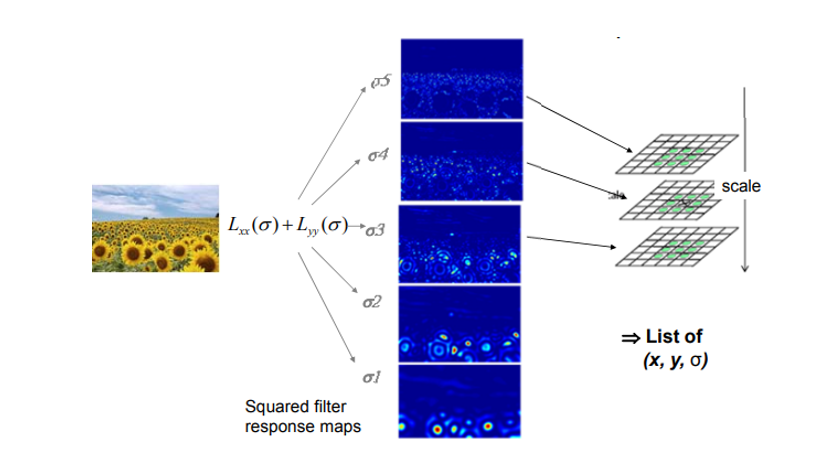
Scale-space blob Detector

원본 이미지는 해바라기들을 찍은 사진으로, 앞쪽은 크게, 멀리 있는건 작게 보인다.

여기서, Laplacian of Gaussian(LoG)를 여러 $\sigma$ 값(스케일)에서 적용한 뒤, 위치(x,y)와 스케일( $\sigma$ )에서 국소 극대값(local maxima)을 찾은 결과이다.

원의 중심: 해바라기 중심(검출된 블롭 위치)
원의 크기 : 해당 위치에서 **가장 강하게 응답한 $\sigma$ 값(즉 characteristic scale)

따라서 큰 해바라기는 큰 원으로, 작은 해바라기는 작은 원으로 표시된다.

즉, 이 결과는 한 장의 이미지 안에서 객체가 다양한 크기로 존재하더라도, Laplacian 응답의 극대값을 이용하면 각각의 해바라기를 "자기 크기에 맞는 스케일"로 잡아낼 수 있다는 것을 보여준다.

즉, 카메라 줌인/줌아웃, 해바라기의 원근감 때문에 크기가 달라져도, 스케일 불변적인 방법으로 동일한 객체(해바라기)를 인식할 수 있다.

Technical Detail

블롭을 검출하기 위해서는 Laplacian of Gaussian(LoG) 필터를 사용해야 하지만, 직접 계산하면 연산량이 크다.

그래서 SIFT 같은 알고리즘에서는 Difference of Gaussians(DoG)를 사용해서 LoG를 근사한다.

식으로 표현하면 아래와 같다.

L(x,y,\sigma) = \sigma^2 \Big(G_{xx}(x,y,\sigma) + G_{yy}(x,y,\sigma)\Big)

DoG(x,y,\sigma) = G(x,y,k\sigma) - G(x,y,\sigma)

즉, 두 개의 다른 $\sigma$ 를 가진 가우시안 필터링 결과를 빼주면 LoG와 유사한 응답을 얻을 수 있고, 훨씬 효율적으로 계산이 가능하다.

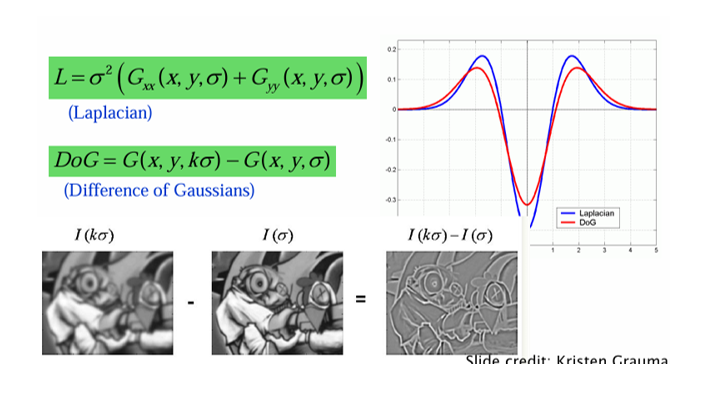
위 이미지의 그래프를 보면, Laplacian과 DoG의 응답 곡선이 거의 겹쳐있음을 알 수 있다. 즉, DoG로 대체가 가능하다는 뜻이다.