[CV] Object Recognition(2) - SVMs

Support Vector Machine (SVM)

서포트 벡터 머신(Support Vector Machine, SVM)은 객체 인식에서 널리 사용된 지도 학습 기반 분류기이다. 기본 아이디어는 학습 데이터에서 각 클래스를 구분할 수 있는 최적의 초평면(hyperplane)을 찾는 것이다.

SVM은 단순히 두 클래스를 나누는 임의의 직선을 찾는 것이 아니라, 클래스 간 마진(margin)을 최대화하는 분리 경계를 설정한다. 이때 경계에 가장 가까이 위치한 데이터 포인트들을 서포트 벡터(support vectors)라 부르며, 실제로 결정 경계를 정의하는 핵심 요소가 된다.

또한 SVM은 커널 함수(kernel function)를 활용해 입력 데이터를 고차원 공간으로 매핑하여, 원래 공간에서는 선형적으로 분리되지 않는 문제도 해결할 수 있다. 이를 통해 선형 분류기의 한계를 극복하면서도, 최근접 이웃 방법보다 계산 효율성을 높였다.

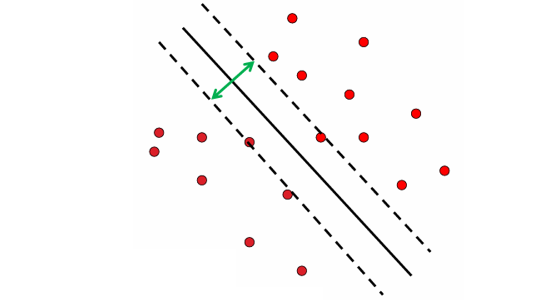
핵심 아이디어

• 서포트 벡터 : 전체 데이터가 아니라, 경계에 가까운 일부 데이터가 결정 경계를 정의한다.
• 마진 최대화 : 가장 안정적인 분리선(일반화 성능이 높은 모델)을 만든다.
• 확장성 : 커널 트릭(Kernel trick)을 활용하면 비선형 데이터도 고차원 공간에서 선형적으로 분리 가능하다.

수학적 표현

데이터가 두 클래스 $(+1, -1)$로 나뉜다고 할 때, SVM은 다음 제약 조건을 가진다.

• 양의 클래스
  $y_i = 1 \,\,\,\to\,\,\,w\cdot x_i + b \ge 1$
• 음의 클래스
  $y_i = -1\,\,\, \to \,\,\, w\cdot x_i + b \le -1$
• 서포트 벡터(support vectors)
  $w\cdot x_i + b = \pm1$

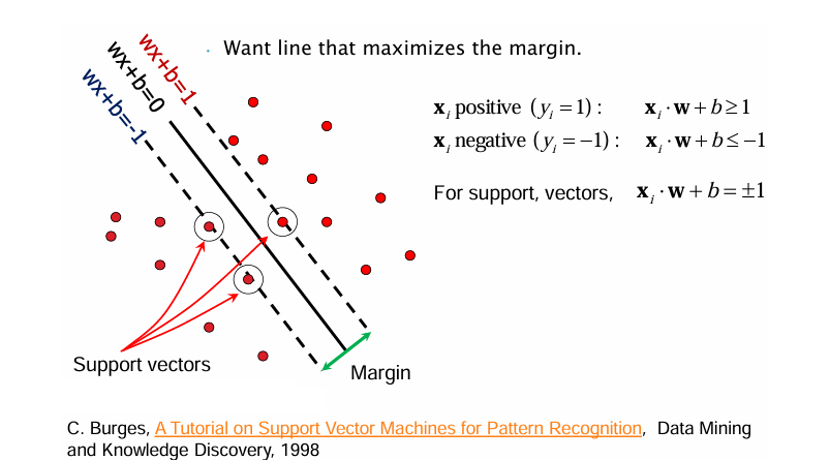
위 그림에서 볼 수 있듯이 원으로 표시된 점들이 서포트 벡터로, 마진을 직접 결정하는 데이터 포인트들이다.

마진(Margin) 최적화

점과 초형면 사이의 거리는

으로 정의된다. 서포트 벡터에 대해 이 값이 최소가 되므로, 마진은

이 된다. 따라서 SVM의 학습 목표는 $||w||$를 최소화하여 마진 $M$을 최대화하는 것이다.

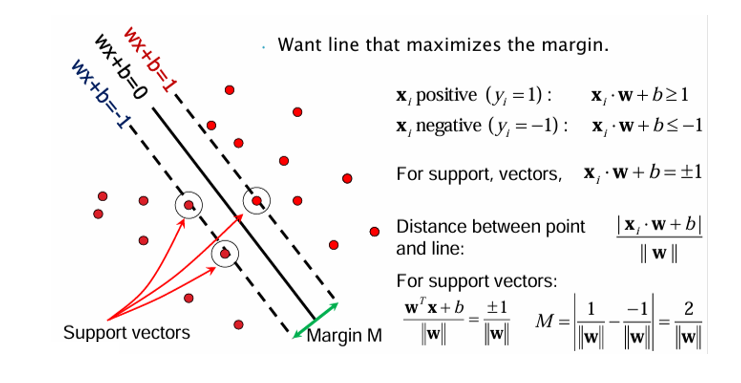
SVM: Maximum Margin Principle

VM의 핵심은 클래스 간의 마진(margin)을 최대화하는 것이다. 마진은 분리 초평면과 서포트 벡터 사이의 거리로 정의되며, 이는 $\frac{2}{\|w\|}$로 표현된다. 따라서 마진을 최대화하는 것은 곧 $\|w\|$를 최소화하는 문제와 같다.

이를 제약 조건과 함께 쓰면,

• 양의 클래스 $(y_i = +1)$:

• 음의 클래스 $(y_i = -1)$:

• 이를 하나의 식으로 정리하면:

따라서 최적화 문제는 Quadratic Optimization 형태로 정리된다:

라그랑지 승수법과 해의 구조

이 최적화 문제를 라그랑지 승수법으로 풀면, 최종적으로 $w$는 서포트 벡터의 선형 결합으로 표현된다.

여기서 $\alpha_i$는 학습 과정에서 얻어지는 가중치이며, $\alpha_i > 0$인 샘플만이 실제 분류 경계에 기여한다. 즉, 모든 데이터가 아니라 서포트 벡터만이 결정 초평면을 정의한다는 점이 중요하다.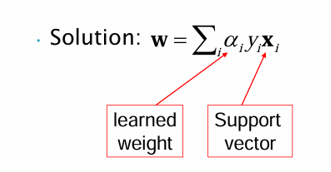

최종 결정 함수

학습이 끝난 후, 새로운 입력 $x$에 대한 분류는 다음과 같이 계산된다.

• $f(x) > 0$이면 positive class
• $f(x) < 0$이면 negative class

즉, 서포트 벡터들과의 내적을 통해 새로운 점의 레이블을 판별한다.

정리하면, SVM은 마진을 최대화하는 최적화 문제로 정의된다. 해는 서포트 벡터의 선형 결합으로 주어지며, 최종 분류는 내적 + 바이어스를 통해 결정된다.

References

C. Burges, A Tutorial on Support Vector Machines for Pattern Recognition and Knowledge Discovery, 1998 Data Mining