[CV] Object Recognition(1) - Introduction & Classification

Yeontachi·2025년 8월 27일

Computer Vision Note

목록 보기

38/47

객체 인식(Object Recognition)은 컴퓨터 비전에서 가장 핵심적이고 오랜 역사를 가진 주제 중 하나이다. 인간은 시각을 통해 자연스럽게 물체를 구분하고 인식하지만, 컴퓨터가 동일한 작업을 수행하기 위해서는 복잡한 알고리즘과 데이터 표현 방식이 필요하다. 객체 인식은 단순히 이미지 내의 물체를 "보는 것"을 넘어서, 그것이 무언인지(분류), 어디에 있는지(탐지),어떤 상태인지(세분화, 포즈, 속성 분석)를 해석하는 과정이다.

객체 인식(Object Recognition)의 어려움

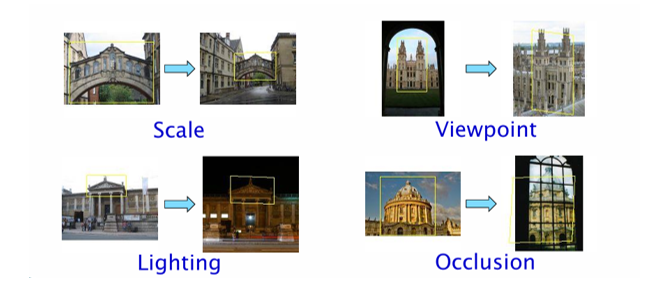
객체 인식은 인간에게는 직관적이고 자연스러운 작업처럼 보이지만, 컴퓨터에게는 여러 가지 이유로 매우 어려운 문제이다. 사용자가 보내준 이미지들은 이러한 어려움을 잘 보여주고 있으며, 각각의 요인을 정리하면 다음과 같다.

크기 변화(Scale)
같은 물체라도 관찰 거리에 따라 영상 속 크기가 크게 달라질 수 있다. 가까이에서 촬영한 물체와 멀리서 촬영한 물체는 픽셀 단위 표현에서 전혀 다른 패턴을 보인다.
시점 변화(Viewpooint Variantion)
같은 물체라도 관찰 각도에 따라 전혀 다른 형태로 보인다. 특히 3차원 물체는 2차원 영상으로 투영되면서 부분적 형태만 드러나거나 심하게 왜곡될 수 있다.
조명 변화(Illumination)
같은 물체라도 빛의 세기, 방향, 색깔에 따라 전혀 다른 픽셀 분포를 보인다.
형태 변형(Deformation)
특히 생물이나 유연한 물체는 비강체(non-rigid) 변형을 겪는다. 같은 물체라도 자세, 움직임에 따라 형태가 달라지므로 인식이 어렵다.
가림 현상(Occlusion)
물체가 다른 물체에 의해 일부 가려질 수 있다. 인식 알고리즘은 보이지 않는 부분을 추론해야 한다.
복잡한 배경(Background Clutter)
물체와 배경이 비슷한 색이나 질감을 가질 경우, 객체와 배경을 구분하기 어렵다.
클래스 내 변이(Intro-class Variation)
같은 범주의 물체라도 모양, 크기, 재질, 색상이 다양한다.

즉, 객체 인식은 스케일, 시점, 조명, 형태 변형, 가림, 복잡한 배경, 클래스 내 다양성과 같은 요인 때문에 난이도가 높다. 이러한 문제들은 전통적인 특징 기반 접근에서는 치명적인 한계로 작용했으며, 오늘날 딥러닝 기반 접근은 대규모 데이터 학습과 표현 학습을 통해 이러한 어려움을 점차 극복해가고 있다.

객체 인식과 머신러닝 프레임워크

객체 인식(Object Recognition)은 단순히 이미지를 해석하는 문제를 넘어서, 주어진 입력을 기반으로 “이것이 무엇인지” 분류하고, 보지 못한 새로운 이미지에서도 올바른 예측을 수행해야 한다. 이 과정에서 머신러닝(Machine Learning) 프레임워크가 핵심적으로 사용된다.

1. 머신러닝의 기본 구조

머신러닝에서의 목표는 입력 벡터 $x$ 를 출력 $y$ 로 매핑하는 함수 $f(x)$ 를 학습하는 것이다.

Feature representation (특징 표현): 이미지에서 의미 있는 특징을 추출한다.
Prediction function (예측 함수): 특징을 입력받아 클래스에 대한 예측을 수행한다.
Output (출력): 최종적으로 클래스 레이블 또는 확률 값이 산출된다.

y = f(x)

여기서 학습 과정은 주어진 데이터셋을 통해 함수 $f$ 를 최적화하는 과정이고, 테스트 과정은 새로운 데이터에 학습된 함수 $f$ 를 적용하는 과정이다.

2. 학습(Training)과 테스트(Testing) 단계

Training: 라벨이 있는 학습 데이터 $\{(x_1, y_1), \dots, (x_N, y_N)\}$ 를 이용해 모델을 학습한다. 목표는 학습 데이터에서 오차를 최소화하는 예측 함수 $f$ 를 찾는 것이다.
Testing: 학습된 $f$ 를 이용해 이전에 보지 못한 입력 $x$ 에 대해 결과 $y=f(x)$ 를 예측한다.

보내준 그림처럼,

훈련 이미지에서 특징을 추출하고,
해당 특징을 학습(label과 함께)하여 모델을 생성한 뒤,
테스트 이미지에서도 같은 특징을 뽑아 모델에 넣어 결과를 얻는 절차를 따른다.

3. 분류(Classification)와 결정 경계

머신러닝에서 객체 인식은 보통 분류 문제(Classification)로 정식화된다.

입력 공간을 여러 개의 **결정 영역(decision regions)**으로 나누고,
각 영역은 특정 클래스에 해당한다.
이 경계를 결정 경계(decision boundary)라 하며, 학습된 모델이 어떤 입력을 어느 영역에 속하게 할지를 결정한다.

예를 들어, 두 개의 특징 차원 $(x_1, x_2)$ 이 있다고 하면, 그림처럼 $R_1, R_2, R_3$ 영역으로 나뉘고, 새로운 입력이 어느 영역에 속하는지에 따라 클래스가 할당된다.

정리

즉, 객체 인식은

입력 이미지를 특징 벡터 $x$ 로 변환하고,
학습 데이터로부터 예측 함수 $f(x)$ 를 최적화하며,
새로운 입력에 대해 출력 $y$ 를 생성하는 과정으로 구성된다.

이는 객체 인식의 전통적 접근(특징 추출 + 분류기 학습)에서 딥러닝 기반 접근(이미지 → 딥러닝 모델이 직접 특징 학습 및 분류)으로 자연스럽게 이어지는 기초 개념이라 할 수 있다.

Classification(분류)

Classification(분류)란 입력 벡터를 두 개 이상의 클래스 중 하나에 할당(assign)하는 과정이다. 예를 들어, 고양이/개를 구분하거나, 숫자 0~9를 인식하는 문제가 분류 문제에 해당한다.

입력 데이터는 여러 특징(feature)으로 이루어진다. 이 특징들은 좌표로 두면 입력 공간(input space)을 얻을 수 있다.

예를 들어 $(x_1, x_2)$ 라는 두 개의 특징을 사용하면 2차원 평면이 입력 공간이 된다. 이 공간에서 각 지점은 하나의 데이터(입력 벡터)를 나타낸다.

모델이 학습되면, 이 입력 공간은 여러 결정 영역(decision regions)으로 나뉜다. 이때 각 영역은 하나의 클래스에 대응되며, 새로운 입력이 어느 영역에 속하는지에 따라 클래스가 결정된다.

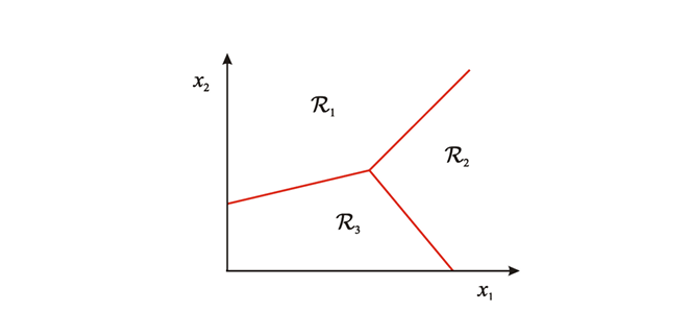
결정 영역 사이에는 경계선(boundary)가 존재한다. 경계는 분류기가 학습한 규칙을 시각화한 것이다. 위 그림에서는 빨간색 선이 세 영역 $R_1, R_2, R_3$ 를 구분하는 결정 경계(decision boundary)를 의미한다.

결정 경계는 여러 형태가 존재한다. 선형 분류기(linear classifier)는 직선(또는 초평면)을 결정경계로 만들며, 복잡한 분류기(예: 딥러닝)는 매우 비선형적인 곡선 형태의 경계를 학습할 수 있다.

K-Nearest Neighbor(K-NN, K-근접 이웃)

객체 인식과 같은 분류 문제를 해결하기 위해 가장 직관적이고 단순한 방법 중 하나가 K-근접 이웃(K-Nearest Neighbor, K-NN) 알고리즘이다. 이 방법은 훈련 데이터와의 "가까움"을 기준으로 새로운 데이터의 레이블을 결정하는 방식이다.

기본 아이디어 - Nearest Neighbor
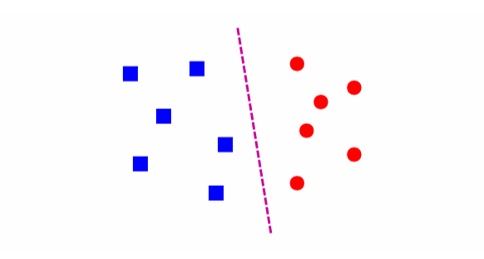
가장 먼저 생각할 수 있는 단순한 방법은 Nearest Neighbor 방식이다. 새로운 데이터가 들어오면, 훈련 데이터 중 가장 가까운 데이터 하나를 찾아 그 레이블을 그대로 할당하는 것이다.

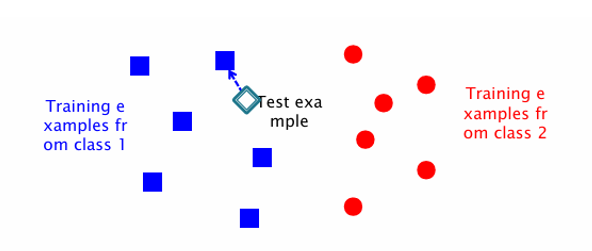
예를 들어, 위 그림에서 파란색 사각형은 클래스1, 빨간색 원은 클래스2를 나타낸다고 하자. 새로운 데이터(다이아몬드)가 들어오면, 가장 가까운 파란색 점을 찾아 클래스 1로 분류한다.

이때 필요한 것은 거리 함수(distance function)이며, 보통 유클리드 거리(Euclidean distance)가 많이 사용된다.

Nearest Neighbor를 공간 전체에 적용하면, 특징 공간(feature space)이 자연스럽게 여러 영역으로 나뉜다. 각 영역은 특정 훈련 데이터와 가까운 영역이며, 새로운 데이터가 어느 영역에 들어가는지에 따라 클래스가 결정된다.

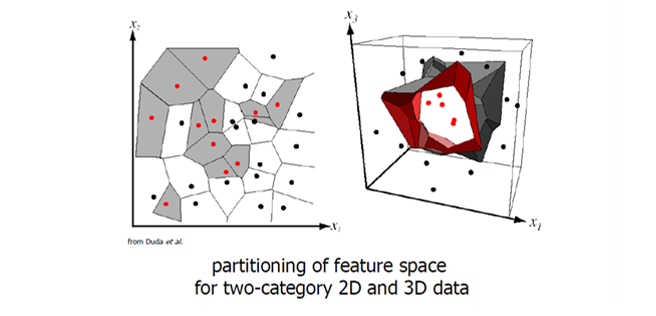
위 그림은 2D와 3D 데이터 공간이 훈련 데이터에 의해 분할된 모습을 보여준다. 이렇게 형성된 영역을 보로노이 다이어그램(Voronoi diagram)이라 한다.

K-Nearest Neighbor
Nearest Neighbor 방식은 직관적이지만, 단일 이웃만 참고하므로 잡음(noise)에 민감하다. 이를 개선한 방법이 K-Nearest Neighbor이다.

새로운 데이터가 들어오면, 훈련 데이터 중 가장 가까운 K개의 점을 찾는다.

그 K개의 점들 중 가장 많이 속한 클래스가 새로운 데이터의 레이블이 된다.(다수결 투표 방식)

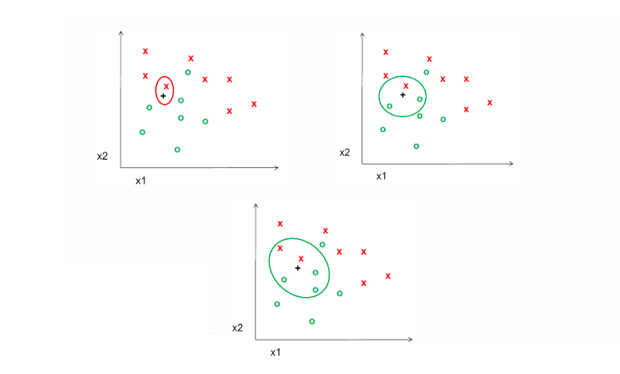
위 그림은 $K$ 가 각각 $K=1, K=3, K=5$ 로 변할 때 결정이 어떻게 달라지는지를 나타낸다.

K-NN은 간단하지만 CIFAR-10과 같은 실제 이미지 데이터셋에서도 동작한다.

위 이미지는 테스트 이미지와 훈련 데이터에서 가장 가까운 10개의 이미지를 나열한 결과를 보여준다. 예를 들어, 테스트 이미지가 자동차라면, 가장 가까운 훈련 샘플 10개 역시 대부분 자동차 이미지로 나타난다.

K-NN은 구현이 매우 간단하고, 학습 과정 없이 데이터를 그대로 저장하고 활용하며, 어떤 형태의 데이터에도 적용이 가능하다는 장점이 있다.

Linear Classifiers

객체 인식에서 데이터를 분류하는 또 다른 기본 방법은 선형 분류기(Linear Classifier)이다. 선형 분류기는 입력 공간에서 직선(2D) 혹은 초평면(Hyperplane, 고차원)을 경계로 두어 서로 다른 클래스를 구분하는 방법이다.

기본 아이디어
선형 분류기의 목표는 데이터를 나눌 수 있는 하나의 선형 함수(linear function)를 찾는 것이다.

수식으로는 다음과 같이 표현된다.

f(x) = \text{sgn}(w\cdot x + b)

여기서 $w$ 는 가중치 벡터, $x$ 는 입력 특징 벡터, $b$ 는 바이어스 항이다. 이 함수는 결과 부호(sign)에 따라 클래스가 결정된다.

아래 이미지를 예로 들어보면, 각 픽셀은 하나의 특징 값으로 변환되고, 모든 픽셀은 하나의 벡터로 연결된다. 여기에 가중치 $W$ 를 곱하고, 바이어스 $b$ 를 더해 계산하면 각 클래스에 대한 점수가 산출된다. 여기서 가장 높은 점수를 갖는 클래스가 최종 결과가 된다.

데이터가 선형적으로 구분 가능(Linearly separable)하다면, 데이터를 나눌 수 있는 직선(또는 초평면)은 여러 개 존재할 수 있다. 하지만 이 중 어떤 분리선이 가장 좋은가?라는 문제가 발생한다.

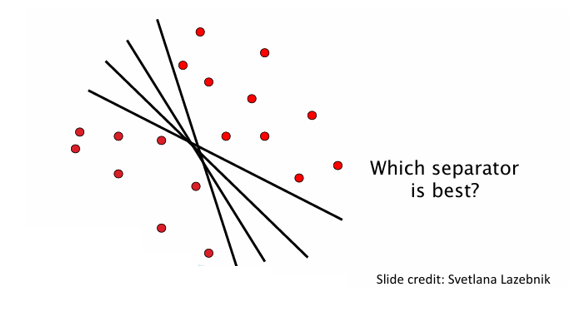
위 그림에서 보면, 동일한 데이터를 여러 직선으로 구분할 수 있다. 그렇다면 여기서 어떤 직선이 좋은 분리선일까?

좋은 분리선을 선택하기 위해서는 마진(margin)을 고려하거나, 분류기의 일반화 능력을 평가하는 기준이 필요하다. 이는 이후 서포트 벡터 머신(SVM)으로 이어지는 중요한 개념이다.

K-NN vs Linear Classifier

객체 인식에서 분류기를 선택할 때는 여러 접근 방법이 존재한다. 그 중 대표적인 것이 위에서 살펴본 K-NN(최근접 이웃)과 Linear Classifier(선형 분류기)이다. 두 방법은 각각의 장단점을 가지고 있으며, 어떤 상황에서 어떤 방법을 택할지에 따라 성능과 효율성이 달라진다.

최근접 이웃(NN, Nearest Neighbor)
최근접 이웃은 새로운 데이터가 들어왔을 때 훈련 데이터와의 거리(distance)를 계산하여 가장 가까운 데이터의 레이블을 그대로 예측에 사용하는 방법이다.

장점
- 구현이 매우 간단하다.
- 결정 경계가 반드시 선형일 필요가 없어 복잡한 형태의 데이터도 구분이 가능하다.
- 클래스 개수에 제한 없이 적용 가능하다.
- 비모수적(nonparametric) 방법으로, 데이터 분포에 대한 가정을 필요로 하지 않는다.
단점
- 좋은 성능을 내기 위해서는 적절한 거리 함수가 필수적이다.
- 테스트 시 모든 훈련 샘플과 거리를 계산해야 하므로 속도가 느리다.

선형 분류기(Linear Classifer)
선형 분류기는 데이터를 나누는 직선(또는 초평면)을 학습하여 클래스 구분을 수행한다.

장점
- 저차원 파라미터 표현으로 모델을 단순하게 유지할 수 있다.
- 한 번 학습된 후에는 테스트 단계에서 매우 빠른 예측이 가능하다.
단점
- 기본적으로 두 클래스 간 분류 문제에 초점이 맞춰져 있다.(다중 클래스는 확장이 필요)
- 선형 함수를 학습하는 방법 자체가 쉽지 않을 수 있다.
- 데이터가 비선형적으로 구분되는 경우에는 단순 선형 분류기로는 성능이 한계에 부딪힌다.