[CV] Principle Component Analysis and Face Recognition(1) - Singular Value Decomposition
Computer Vision Note

특이값 분해(Singular Value Decompoosition, SVD)는 임의의 행렬을 세 개의 행렬 곱으로 분해하는 기법으로, 선형대수학과 데이터 분석 전반에서 매우 중요한 역할을 한다. 기본적으로 하나의 행렬 를 직교(orthohonal) 성질을 가진 행렬들과 대각(diagonal) 행렬의 곱으로 표현할 수 있으며, 이를 통해 행렬의 구조적 성질을 명확히 파악할 수 있다.
Singular Value Decomposition(SVD)
행렬 분해(Matrix Factorization)는 하나의 복잡한 행렬을 보다 단순한 구조를 가진 행렬들의 곱으로 표현하는 과정이다. 이 중 가장 널리 사용되고 강력한 기법이 바로 특이값 분해(SVD, Singular Value Decomposition)이다.
기본 정의
임의의 행렬 는 다음과 같이 세 개의 행렬 곱으로 분해된다.
- : 직교(unitary) 행렬
- : 대각 행렬, 대각 원소는 특이값(singular values)
- : 직교(unitary) 행렬
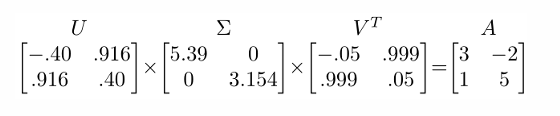
행렬의 의미
회전 행렬(rotation matrices)로 일반적으로 직교 행렬(orthogonal matrices)로 해석된다. 각 열은 단위 벡터(unit vector)이며, 데이터를 다른 방향으로 "회전"시키는 역할을 한다.
대각 행렬이며, 대각 성분은 내림차순으로 정렬된 특이값(singular values)이다.- 특이값이 0이 아닌 원소의 개수 = 의 rank
- 값이 클수록 데이터의 주요 변동성을 설명하는 방향을 의미한다.
차원과 구조
가 행렬일 때,
즉, 분해 후에도 원래 행렬 의 크기와 동일하게 다시 결합된다.
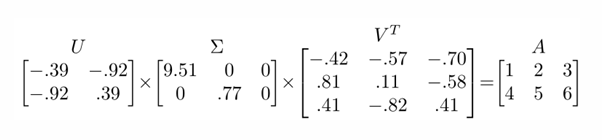
직관적 해석
- 선형 변환의 분해
행렬 의 작용은 먼저 를 통한 좌표계 변환(회전), 이어서 를 통한 축 방향 스케일링, 마지막으로 를 통한 또 다른 회전으로 이해할 수 있다. - 주요 성분(Principal Components)
의 첫 몇 개의 열 벡터는 데이터의 주요 패턴(주성분)을 설명한다. 따라서 고차원 데이터를 몇 개의 주요 축으로 근사 가능하다.
SVD Applications
특이값 분해(SVD)는 단순히 행렬을 분해하는 수학적 도구에 그치지 않고, 실제 데이터 분석압축패턴 인식에 직접적으로 활용된다. 핵심 아이디어는 모든 데이터를 완벽하게 복원하지 않고, 주요 성분(Principal Components)만으로 근사하는 것이다.
행렬의 부분 근사(Low-rank Approximation)
행렬 는 로 분해되며, 이는 사실상 를 의 열벡터(기저, biasis)의 선형 결합으로 표현하는 것과 같다.
모든 열벡터를 사용하면 를 완벽하게 복원할 수 있지만, 실제 데이터에서는 앞부분의 몇 개 벡터(큰 특이값에 해당하는 성분)만으로도 충분히 근사할 수 있다.
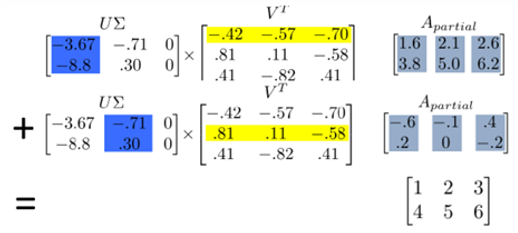
위 수식에서 볼 수 있듯이, 첫 번째 주성분만으로 만든 는 원래 행렬과 비슷한 구조를 유지한다.
주성분(Principal Components)과의 관계
의 처음 몇 개 열벡터는 데이터를 설명하는 주요 패턴(Principal Components)이다.
의 각 행은 이러한 패턴이 어떻게 결합되어 원래 행렬의 열을 생성하는지를 보여준다.
즉, SVD는 PCA와 동일한 차원 축소 메커니즘을 제공한다.
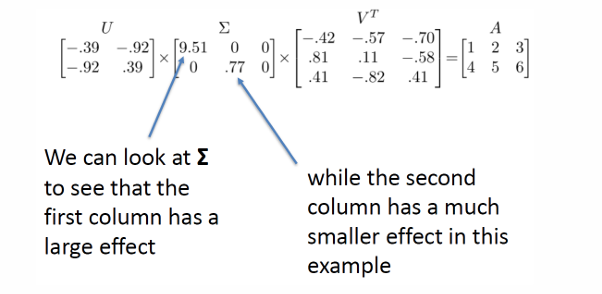
특이값의 크기와 중요도
의 대각 원소(특이값)는 각 주성분이 데이터를 설명하는 중요도(variance 크기)를 나타낸다.
값이 클수록 해당 성분이 큰 비중을 차지하며, 값이 작은 경우 무시해도 큰 정보 손실이 없다.
아래 예시에서 첫 번째 특이값 9.51은 두 번째 0.77보다 훨씬 크므로, 첫 번째 성분이 데이터를 거의 다 설명한다.
이미지 압축(Image Compression)
실제 이미지 데이터는 수천 개의 차원을 가진 행렬로 표현되지만, 대부분의 정보는 소수의 주성분으로 설명된다.

위 이미지는 300개 주성분 중 상위 10개만 사용해도 원래 이미지를 어느 정도 인식 가능한 수준으로 복원할 수 있다.
따라서 SVD는 이미지 압축 및 노이즈 제거에도 효과적으로 활용된다.
Principal Component Analysis(PCA)
PCA(주성분 분석)는 데이터에 내재된 중요한 패턴(Principal Components)을 찾아내어, 데이터를 보다 간단하고 효율적으로 표현하는 차원 축소 기법이다. PCA는 본질적으로 SVD(Singular Value Decomposition)와 밀접하게 연결되어 있다.
SVD와의 관계
SVD에서 의 각 열벡터는 데이터의 주성분(Principal Components) 역할을 한다.
원래 데이터 행렬을 로 분해했을 때,
는 데이터의 주요 패턴을 담고 있으며,
는 각 패천이 데이터를 설명하는 "중요도(분산 크기)"를 나타내고,
는 각 데이터 샘플이 이 패턴들에 어떻게 결합되는지를 나타낸다.
즉, PCA는 데이터를 새로운 좌표계(주성분 축)로 변환하여, 불필요한 중복 정보를 줄인다.
PCA 과정
- 데이터 행렬을 준비한다.(열 = 데이터 샘플, 행 = 특징)
- SVD를 수행하여 로 분해한다.
- 에서 큰 값에 해당하는 몇 개의 성분만 선택한다.
- 의 해당 열들을 이용하여 데이터를 저차원 근사 표현으로 변환한다.
의미와 장점
-
중복 제거
원시 데이터(raw data)는 많은 중복과 잡음을 포함한다. PCA는 분산이 큰 축(즉, 정보량이 많은 축)만 남겨 데이터의 본질적 구조를 보존한다. -
효율적 표현
원본 데이터 대신, 주성분에 대한 가중치(Projection Coefficients)로 데이터를 표현할 수 있다. -
계산 효율성
데이터 차원을 크게 줄이면 머신러닝 알고리즘의 학습과 추론 속도가 빨라지고, 과적합 위험도 줄어든다.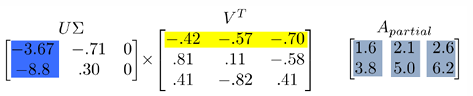
위 예시를 보면,
는 데이터의 주요 성분(패턴)을 담고 있다.
는 이러한 성분이 어떤 비율로 결합되어 각 샘플을 형성하는지 나타낸다.
따라서 은 주성분 일부만 사용한 근사 행렬이며, 원본 데이터를 압축 표현한 것이다.
정리하면, PCA는 SVD를 기반으로 데이터의 공통 패턴을 추출하고, 이를 통해 차원을 축소하는 기법이다. 주요 패턴이 보존되고, 불필요한 정보는 제거되어 효율적인 데이터 표현이 가능하다. 또한 머신러닝 및 비전 응용에서 성능을 향상 시킨다.
