LSQ, Learned Step Size Quantization(ICLR, 2020) paper review

딥러닝 모델은 이미지 분류, 음성 인식, 자율 주행 등 다양한 분야에서 뛰어난 성능을 보여주지만, 연산량과 메모리 사용량이 매우 크다는 단점이 있다.

이를 줄이기 위해 양자화(Quantization), 즉 가중치와 활성값을 낮은 정밀도의 정수(예: 8bit, 4bit)로 표현하는 연구가 활발히 진행되었다.

문제는, 단순히 비트를 줄이면 모델 정확도가 크게 떨어진다는 점이다. 특히 2~4비트 같은 초저비트 환경에서는 성능 손실을 막는 것이 쉽지 않았다.

기존 연구들은,
고정된 스텝 크기(Step size)로 양자화, 데이터 분포 기반으로 양자화 구간을 설정(quantization error 최소화), 백프로파게이션을 활용해 양자화 구간 학습(task loss 기반 최적화 시도) 등의 방향으로 진행되었다.

그러나 여전히 한계가 존재하였고, 양자화 스텝 크기(Step size)를 어떻게 학습할 것인가?가 핵심 문제였다.

LSQ의 핵심 아이디어

딥러닝 모델을 저비트로 양자화할 때 가장 중요한 요소 중 하나는 스텝 크기(Step Size)이다. 스텝 크기는 쉽게 말해 "양자화 눈금의 간격"이라고 할 수 있다.

실수 값 $v$를 양자화하는 기본 수식은 다음과 같다.

• $\bar{v}$ : 정수 표현(양자화된 값)
• $\hat{v}$ : 복원된 값(실제 연산에서 사용)
• $Q_N, Q_P$ : 비트 수에 따른 최소/최대 정수 값

즉, 실수 $v$를 스텝 크기 $s$로 나누고, 클리핑 후 반올림하여 정수로 만든 뒤, 다시 $s$를 곱해 복원하는 과정이다.

눈금이 넓으면 표현은 거칠어지고, 눈금이 좁으면 값이 자꾸 잘려나가게 된다.(클리핑) 따라서 적절한 스텝 크기를 잡는 것이 성능을 좌우한다.

문제는, 좋은 스텝 크기를 사람이 직접 정하기 어렵다는 것이다. 지금까지는(~2020) 데이터의 분포나 경험적인 규칙에 의존해 왔다. 하지만 이 방식으로는 "양자화 오차(error)"만 줄일 뿐, 실제 우리가 원하는 "과제 성능(task accuracy)"와 꼭 일치하지는 않았다.

LSQ의 발상은 단순하다.

"가중치나 편향처럼 스텝 크기 $s$도 학습 가능한 파라미터로 두자. 그리고 모델이 task loss을 줄이는 방향으로 $s$를 함께 업데이트하게 하자"

즉, 스텝 크기를 사람이 정하는 값이 아니라 네트워크가 스스로 배우는 값으로 만든 것이다. 학습 과정에서 $s$가 계속 조정되면서, 결과적으로 모델이 성능을 가장 잘 내는 눈금을 찾아간다.

경계에서 민감하게 반응하는 Gradient

하지만 한 가지 난관이 있다. 스텝 크기를 학습하려면, 손실에 대해 $s$가 얼마나 민감한지(gradient)를 계산해야 한다.

그런데 양자화에는 "반올림(round)"이 들어가고, 반올림은 미분이 되지 않는다.

LSQ는 여기서 Straight-Through Estimator(STE)라는 트릭을 사용한다. 반올림 부분은 그냥 "통과"시킨다고 가정하고, 나머지는 정상적으로 미분하는 것이다. 이 과정에서 LSQ는 기존 방법보다 한 발 더 나아간다.
양자화 경계(transition point)에 가까운 값일수록 작은 변화에도 양자화 결과가 확 달라지므로, 그럴 때 $s$에 대한 기울기를 크게 잡아준다. 반대로 경계에서 멀리 떨어진 값은 민감도가 낮다.

이를 수식으로 표현하면 다음과 같다.

여기서 볼 수 있듯이, 입력 값 $v$가 경계에 가까울수록 기울기 크기가 커진다.
즉, 경계 부근에서 스텝 크기 학습이 훨씬 민감하게 일어나도록 설계된 것이다.

시각적으로 확인을 해보면,

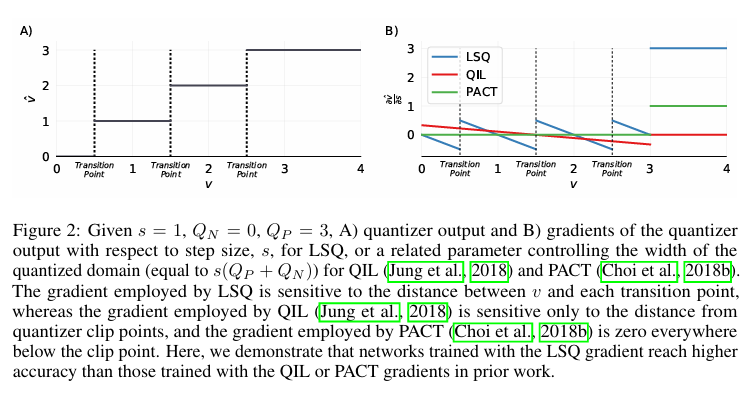
(A) 그래프는 입력 $v$가 스텝 크기 $s$에 의해 어떤 정수 값으로 양자화되는지를 보여준다. $s=1, Q_N = 0, Q_P=3$인 경우, 구간마다 값이 정수(0,1,2,3)로 "뛰어" 올라간다.

(B) 그래프는 스텝 크기 $s$에 대한 기울기를 비교한 것이다.
LSQ(파란색)은 입력 값이 경계에 가까워질수록 기울기가 커진다. 즉, 작은 변화에도 양자화 상태가 변하므로 민감하게 반응한다.
QIL(빨간색)은 클리핑 지점에만 만감하게 반응한다. 경계 내부에서는 변화를 잘 포착하지 못한다.
PACT(초록색)은 클리핑 이전 영역에서 기울기가 0이다. 즉, 대부분의 값에 대해서 스텝 크기 학습이 이뤄지지 않는다.

즉, LSQ의 기울기는 입력 값과 경계 사이의 거리를 반영하기 때문에 더 세밀하게 스텝 크기를 조정할 수 있고, 이는 실제 실험에서도 QIL이나 PACT보다 더 높은 정확도로 이어진다.

가중치와 균형 맞추기

또 하나의 아이디어는 업데이트 크기의 균형이다.
만약 스텝 크기 $s$가 가중치보다 훨씬 크게 움직이면, 학습이 불안정해지고 성능이 떨어진다. LSQ는 수학적으로 "가중치 업데이트 크기: 스텝 크기 업데이트 크기" 비율을 분석하고, 이를 비슷하게 맞추기 위한 스케일링 계수를 제안한다. 간단히 말해, 레이어의 크기와 양자화 레벨 수를 고려해 $s$의 기울기를 적절히 줄여 주는 것이다.

• $N$: 해당 레이어의 파라미터 개수 (가중치 수 $N_W$ 또는 feature 수 $N_F$)
• $Q_P$: 양자화 가능한 정수 레벨 개수

이 계수를 곱해 주면, $s$의 업데이트 크기가 가중치와 비슷한 비율로 맞춰져 학습이 안정화된다.

즉, 정리하면 LSQ는 스텝 크기를 학습 파라미터로 두고, 경계 민감도를 반영한 기울기와 스케일링으로 안정적으로 학습시킨다.

이 단순하지만 강력한 아이디어 덕분에, 2~4비트 초저비트 양자화에서도 성능 손실을 최소화할 수 있었다.

실험 및 결과

LSQ는 단순히 아이디어 차원에서 끝난 것이 아니라, 실제 ImageNet 대규모 데이터셋과 다양한 네트워크 아키텍처(ResNet, VGG, SqueezeNext 등)에 적용해서 실험을 진행하였다. 그 결과는 기존 모든 저비트 양자화 방법보다 뛰어났다.

2~4비트에서 SOTA 달성

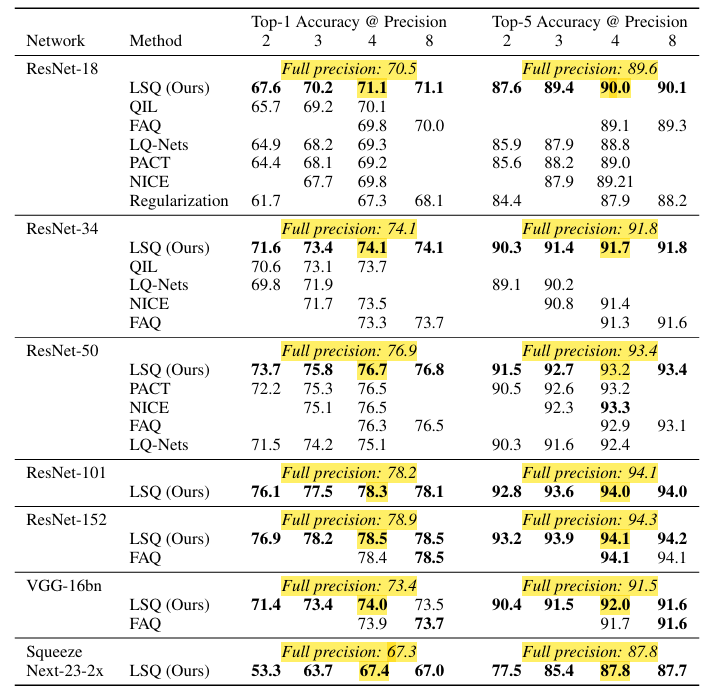
LSQ는 2비트, 3비트, 4비트 환경에서 모두 이전 연구 대비 가장 높은 정확도를 달성했다. 특히 4비트 모델은 Full-Precision(32비트) 모델과 거의 동일한 정확도를 기록했다.

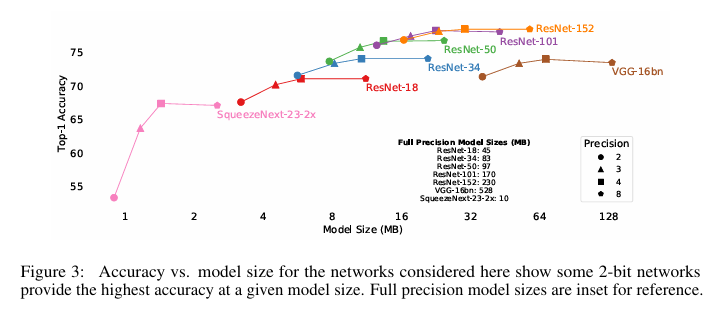
모델 크기 VS 성능

실제 배포에서는 모델 크기도 중요한 제약 조건이다. LSQ는 같은 메모리 크기 안에서 더 높은 정확도를 제공할 수 있었다.

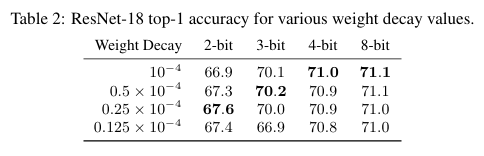
가중치 감쇠(Weight Decay) 조정

저비트 모델은 이미 정밀도가 낮기 때문에 과적합(Overfitting) 위험이 줄어든다.
따라서 정규화 항인 weight Decay를 줄이는 것이 유리했다.

ResNet18 실험에서,

• 3-bit 네트워크 > weight decay를 절반으로 줄였을 때 가장 높은 정확도
• 2-bit 네트워크 > 1/4로 줄였을 때 성능 최적

즉, 정규화 강도를 낮추는 것이 저정밀 네트워크 학습에 도움이 된다.

Gradient Scaling의 효과

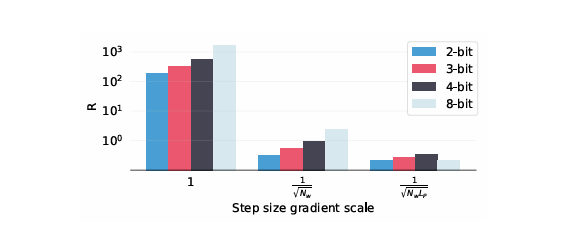
앞서 설명한 스텝 크기 Gradient Scaling은 단순한 트릭이 아니라 실제로 학습 안정성과 성능에 큰 차이를 만들었다.

• 스케일링을 적용하지 않으면, 스텝 크기 업데이트가 가중치보다 100~1000배 커져 학습이 발산하거나 수렴이 느려졌다.

• 제안한 스케일링 $(g = 1/\sqrt{NQ_P})$를 적용했을 때, 모든 정밀도에서 안정적으로 수렴하고 최고의 정확도를 달성했다.

  

양자화 오차 최소화 $\ne$ 성능 최적화

LSQ가 학습한 최종 스텝 크기는 MSE, MAE, KL Divergence 기준으로 오차를 최소화하는 값과 다르다.
그럼에도 불구하고 실제 정확도는 더 높았다.
즉, 데이터 분포를 맞추는 것(오차 최소화)이 곧 성능 향상으로 이어지지 않는다는 사실을 보여주었다.(Task Loss에 직접 맞춘 학습이 더 중요하다.)

지식 증류(Knowledge Distillation)와 결합

추가 실험에서, LSQ를 지식 증류(KD)와 함께 사용했을 때 성능이 더 높았다.

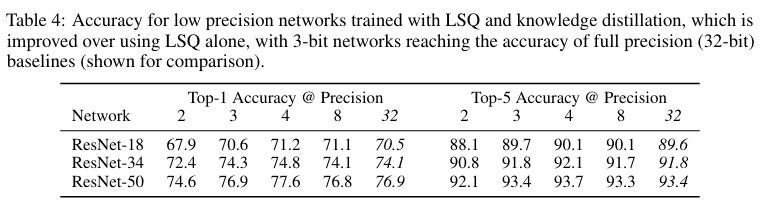
즉, 초저비트 환경에서도 KD와의 결합으로 Full-precision 수준을 도달할 수 있다는 가능성을 보였다.

Conclusions

LSQ는 단순하지만 강력한 발상으로, 초저비트 양자화의 가능성을 크게 확장시킨 연구다. 스텝 크기를 학습 파라미터로 두고, 경계 민감도와 스케일링을 반영해 안정적으로 학습하도록 만든 결과, 3비트 모델이 풀프리시전과 동등한 성능을 달성하는 이정표를 세웠다.

이 연구의 의의는 세 가지로 요약할 수 있다.
첫째, 모바일·엣지 환경처럼 자원 제약이 큰 실제 배포 환경에 적합한 솔루션을 제시했다.
둘째, 단순히 양자화 오차를 줄이는 것이 아니라, 태스크 성능 중심의 학습 접근이 더 효과적임을 실험으로 입증했다.
셋째, 2~3비트 초저비트 영역에서도 충분히 실용적인 성능을 낼 수 있음을 보여주어 이후 연구들의 초석이 되었다.

정리하면, LSQ는 “양자화 오차 최소화”에서 “성능 최적화”로 연구의 패러다임을 이동시킨 전환점이라 할 수 있다. 이후 등장한 AWQ, QLoRA, Structured Quantization 같은 기법들도 이 철학을 이어받아 발전해 나가고 있다.

References

Esser, S. K., McKinstry, J. L., Bablani, D., Appuswamy, R., & Modha, D. S. (2020). Learned step size quantization. Proceedings of the International Conference on Learning Representations (ICLR 2020). https://arxiv.org/abs/1902.08153