Up or Down? Adaptive Rounding for Post-Training Quantization(2020) Paper Review

Yeontachi·2025년 9월 6일

Vision을 위한 Quantization

목록 보기

6/10

딥러닝 모델은 이제 이미지 분류, 번역, 음성 인식, 추천 시스템 등 다양한 분야에서 표준 도구처럼 쓰이고 있다. 하지만 이러한 성능 뒤에는 높은 연산량과 메모리 사용량이라는 부담이 따라온다. 대규모 모델을 클라우드에서 실행하면 인프라 비용이 커지고, 모바일이나 IoT 같은 작은 디바이스에서는 실행 자체가 어렵다.

이를 해결하기 위한 대표적인 접근이 바로 Quantization(양자화)이다. 즉, 네트워크의 weight와 activation을 낮은 비트 정밀도(int8, int4 등)로 표현해 연산과 메모리 전송을 효율화하는 것이다. 하지만 단순히 비트를 줄이면 잡음(noise)이 생기고, 이는 곧 정확도 하락으로 이어진다.

기존 연구는 이를 최소화하기 위해 두 가지 방향으로 발전해왔다.

QAT(Quantization-Aware Training) : 학습 과정에서 양자화를 시뮬레이션하며 훈련한다. 정확도는 높지만, 모델을 다시 학습해야 해서 비용과 시간이 많이 든다.
PTQ(Post-Training Quantization) : 학습이 끝난 모델에 사후적으로 양자화를 적용한다. 데이터와 시간이 거의 필요 없어서 실제 배포(deployment)에 유리하다.

이 중, PTQ의 가장 기본적이면서 널리 쓰이는 방식은 round-to-nearest(가장 가까운 grid 값으로 반올림)이다. 예를 들어, weight가 0.46이고 양자화 step size가 0.25라면 0.5로 올리고, 0.37이라면 0.25로 내린다.

이 논문 이전까지는 이 방식이 최적이라고 생각되었지만, Adaround 논문 저자들은 round-to-nearest가 반드시 최적이 아니라고 한다.

즉, 각 weight를 개별적으로 반올림했을 때보다, Layer 전체 혹은 네트워크 전체 관점에서 task loss를 최소화하는 방향으로 weight를 올릴지 내릴지 선택하는 것이 더 낫다라고 주장한다.

위 아이디어를 토대로, Adaptive Rounding(AdaRound)라는 새로운 PTQ 방법을 제안한다.

AdaRound는
task loss 기반으로 rounding 방향을 조정하고, 소량의 unlabeled data만 사용하며, fine-tuning 없이도 4-bit quantization에서 ResNet18/50을 거의 정확도 손실 없이 유지할 수 있음을 보여준다.

Why Round-to-nearest is Sub-optimal?

그렇다면 왜 round-to-nearest가 sub-optima인지 확인해보자.

Weight perturbation과 Loss 변화

학습이 끝난 모델의 weight를 $w$ , 양자화로 인해 생기는 작은 변화(perturbation)을 $\Delta w$ 라고 해보자.

Task Loss $L(x,y,w)$ 의 변화를 2차 테일러 전개(Taylor expansion)로 근사하면,

\Delta L \approx \Delta w^T g(w) + \frac{1}{2}\Delta w^T H(w) \Delta w

여기서, $g(w)$ 는 gradient, $H(w)$ 는 Hessian이다.
학습이 끝난 모델은 gradient가 거의 0이므로, loss 변화는 주로 Hessian 항(이차항)에 의해 결정된다.

Off-diagonal 항의 존재

Hessian의 대각 항(diagonal term)은 각 weight의 perturbation 크기만 고려한다.(이 경우는 round-to-nearest가 합리적이다.)
하지만, 비대각 항(off-diagonal term)은 weight perturbation 간의 상호작용을 반영한다.

예를 들어, 어떤 weight는 올리고, 다른 weight는 내렸을 때 서로 보상 효과가 생겨 loss 증가를 줄일 수 있다.

반대로, 모두 같은 방향으로 올리거나 내리면 오히려 손해가 된다.

예를 들어, 두 weight $w_1, w_2$ 가 있다고 가정하자.
Hessian이 다음과 같다면,

H^{(w)} = \begin{bmatrix}1 & 0.5\\0.5 & 1 \end{bmatrix}

Loss 변화는

\Delta w^T \cdot H^{(w)} \cdot \Delta w = \Delta w_1^2 + \Delta w_2^2 + \Delta w_1\Delta w_2

여기서 $\Delta w_1$ 과 $\Delta w_2$ 의 부호가 달라야(loss 감소 효과) 더 좋은 결과가 나온다.

즉, 단순히 각 weight를 최근접값으로 round하는 방식은 이 상호작용 효과를 무시하기 때문에 최적이 아니다.

실험적 관찰

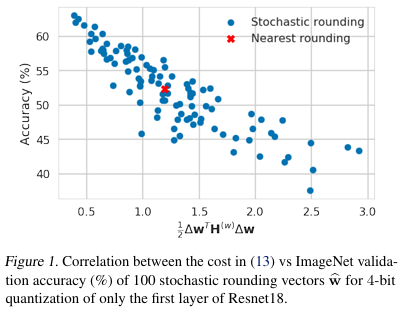
ResNet18 첫 번째 layer를 4-bit로 quantization할 때, 다양한 stochastic rounding 방법을 시도한 결과,

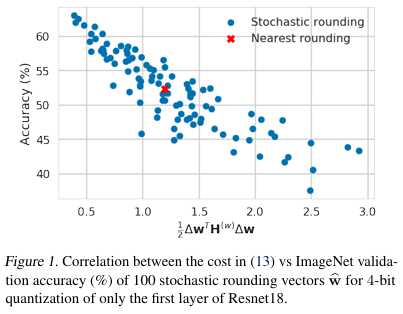
round-to-nearest보다 더 좋은 조합이 100번 중 절반 가까이 존재했고, 최적의 조합은 10% 이상 정확도 향상을 보였다.

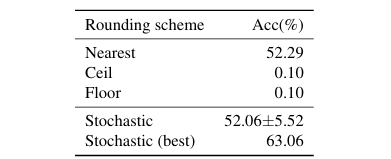
이는 곧 "rounding 방향만 잘 정해도 큰 차이를 만들 수 있다."는 것을 의미한다.

따라서 중요한 것은 per-weight 오차 최소화가 아니라, 전체 loss 기준으로 "어떤 weight는 올리고, 어떤 weight는 내릴지"를 잘 결정하는 것이다.

Method - AdaRound

Task Loss 기반 Rounding

PTQ에서 이 논문의 목표는 양자화로 인한 성능 손실을 최소화하는 것이다.

weight $w$ 를 양자화하면, $\hat{w}$ 는 두 가지 선택지만 가진다.

\hat{w}_i \in \{w_{i,floor}, w_{i,ceil}\}

즉, 각 weight는 step size를 기준으로 "올릴지(floor)" 또는 "내릴지(ceil)"만 정하면 된다.

따라서 문제는 다음 Binary Optimization으로 표현된다.

\text{min}_{\Delta w}\; \mathbb{E}[L(x,y,w + \Delta w) - L(x,y,w)]

여기서 $\Delta w = w - \hat{w}$ 는 quantization 오차이다.

하지만 이 문제를 직접 풀려면 매번 forward pass를 해야 하므로 계산량이 너무 크다. 따라서 저자들은 2차 Taylor 전개 근사를 다시 활용해, 이를 QUBO(Quadraric Unconstrained Binary Optimization) 문제로 변환한다.

\text{min}_{\Delta w} \; E[\Delta w^T H(w)\Delta w]

즉, "각 weight를 위로 올릴지, 아래로 내릴지"를 결정하는 문제를 Hessian 기반 QUBO로 재정의한 것이다.

Local Loss 근사

하지만 QUBO를 풀 때 두 가지 문제가 있다.

계산량이 너무 크다(Hessian은 거대한 행렬)
NP-hard 문제라서 weight 수가 많아지면 풀 수 없다.

이를 해결하기 위해, 이 논문의 저자들은 layer-wise local loss라는 근사 방식을 제안한다.

Hessian을 "block diagonal"로 가정하여 layer간 상호 작용은 무시한다.

$\nabla_z^2 L$ (pre-activation에 대한 Hessian)을 diagonal + 상수라고 단순화한다.

이렇게 하면 문제는 각 레이어의 출력 pre-activation $z$ 의 MSE를 최소화하는 형태로 변한다.

\text{min}_{\Delta W} \; E[(\Delta W x)^2]

즉, "각 weight rounding 방향을 어떻게 정하면, 해당 레이어 출력이 원래와 가장 비슷할까?"로 단순화 된다.

Continouos Relaxation

여전히 문제는 discrete(0=내림, 1=올림) binary 변수라 풀기 어렵다.

따라서 저자들은 이를 연속 변수로 완화(relaxation)한다.

각 weight에 대해 soft rounding 변수 $h(V_{i,j}) \in [0,1]$ 를 둔다.

최적화 과정에서 $h(V_{i,j})$ 는 연속적으로 변하지만, 학습이 끝나면 결국 0(내림) 또는 1(올림)으로 수렴하게 만든다.

Soft quantized weight는

\tilde{W} = s \cdot \text{clip}\left( \left\lfloor \frac{W}{s} \right\rfloor + h(V), \; n, \; p \right).

여기서 $h(V)$ 는 Rectified Sigmoid 함수로 매핑되며, 학습 과정에서 0 또는 1로 수렴하도록 regularization term을 추가한다.

f_{reg}(V) = \sum (1-|2h(V_{i,j}) - 1|^{\beta})

초반엔 자유롭게 움직이며 MSE 최적화에 집중한다.

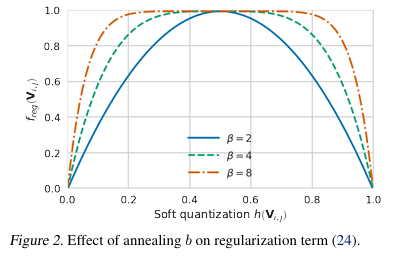
위 그래프를 보면, $\beta$ 값에 따라 regularization 곡선이 달라지고, annealing을 통해 초반에는 자유롭게 움직이다가 후반에는 극단값(0또는 1)으로 수렴하도록 유도한다.
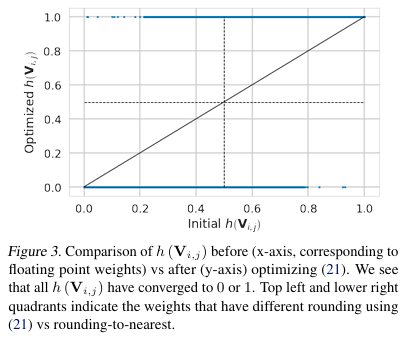
최적화 과정에서 $h(V_{i,h})$ 는 연속적으로 변하지만, 학습이 끝나면 결국 0또는 1로 수렴한다.

최종 최적화 목표는

\min_{V} \; \Big\| f_a(Wx) - f_a(\tilde{W}\hat{x}) \Big\|_F^2 + \lambda f_{\text{reg}}(V)

여기서 $f_a$ 는 활성화 함수(ReLU 등)
$\hat{x}$ 는 이전 레이어가 이미 quantized된 입력

즉, AdaRound는 단순히 per-weight 차이를 줄이는 것이 아니라, layer output reconstruction + task loss 근사를 동시에 고려한다는 점이 핵심이다.

Experiments

이 논문의 저자들은 AdaRound의 성능을 다양한 모델과 작업에 대해 검증했다. 실험의 목적은 크게 3가지이다.

제안한 근사 방법(local loss, relaxation 등)이 실제로 효과적인지 검증
기존 PTQ 기법들과 비교해 AdaRound의 성능 우위 확인
데이터 의존성(unlabeled data 개수, 다른 데이터셋 사용 가능성 등) 평가

Ablation Study

ResNet18 + ImageNet 실험에서, rounding-to-nearest 대비 다양한 근사 방법을 비교

결과 : Local MSE loss 근사와 Continuous Relaxation을 적용한 AdaRound가 성능 $\cdot$ 계산 효율 모두에서 우수했다.

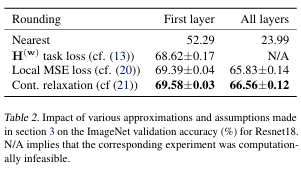
Design Choices

Regularization과 activation 반영 여부가 성능에 미치는 영향을 분석

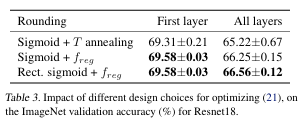
Rectified Sigmoid + regularization이 가장 안정적
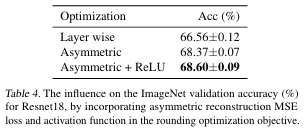
Asymmetric reconstruction loss 적용 시 추가 성능 향상

Comparison with Other PTQ Methods

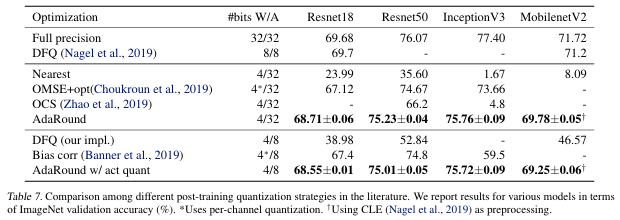
기존 PTQ(DFQ, Bias correction 등) 대비, AdaRound가 4-bit weight-only quantization에서 가장 높은 정확도를 보였다.

ResNet18/50은 FP32 대비 1% 이내 손실하였고, InceptionV3/MobileNetV2는 2%이내였다.

Roubustness to Data

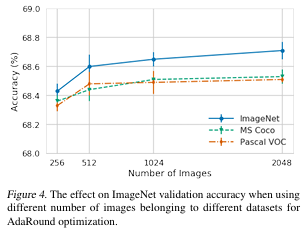
256장 미만의 unlabeled data로도 FP32 대비 2% 이내 성능을 유지하였고, 다른 데이터셋(Pascal VOC, MS COCO) 사용해도 성능이 유지되었다.

Semantic Segmentation

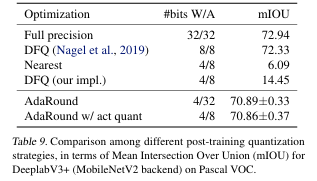
DeeplabV3 + (MobileNetV2 backbone)에도 적용,
4-bit weight + 8-bit activation에서도 FP32 대비 성능 손실이 약 2%에 불과했다.

References

Nagel, M., Amjad, R. A., van Baalen, M., Louizos, C., & Blankevoort, T. (2020). Up or Down? Adaptive Rounding for Post-Training Quantization. arXiv preprint arXiv:2004.10568. https://arxiv.org/abs/2004.10568