선형대수 : 02 행렬 - 2 : 행렬의 계산

yeppi1802·2024년 6월 6일
선형대수제로베이스
0

선형대수_제로베이스 데이터 분석 스쿨

목록 보기
4/12

❇️ 요약

  • 행렬의 덧셈, 뺄셈
  • 행렬의 곱셈
  • 전치 행렬
  • 역행렬

📖 행렬의 덧셈 뺄셈

🔆 행렬의 덧셈 뺄셈

  • 행렬의 더하기와 빼기는 간단함
  • 위치가 같은 원소들끼리 더해줌. 단, 행렬의 크기가 동일해야함
A=(a11a12a21a22),B=(b11b12b21b22)A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, \qquad B=\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}
⇒A±B=(a11±b11a12±b12a21±b21a22±b22)\\\Rightarrow A\pm B=\begin{pmatrix} a_{11}\pm b_{11} & a_{12}\pm b_{12} \\ a_{21}\pm b_{21} & a_{22}\pm b_{22} \end{pmatrix}

수식 : A±B=(amn)±(bmn)=(amn±bmn)A\pm B= (a_{mn})\pm(b_{mn})=(a_{mn}\pm b_{mn})

📖 행렬의 곱셈

🔆 행렬의 상수배

  • 행렬 A의 상수배 kA는 행렬 A의 각 성분에 임의의 실수 K를 곱함
kA=[ka11ka12⋯ka1nka21ka22⋯ka2n⋮⋮⋱⋮kam1kam2⋯kamn]kA=\begin{bmatrix} ka_{11} & ka_{12}&\cdots&ka_{1n} \\ ka_{21} & ka_{22}&\cdots&ka_{2n} \\ \vdots & \vdots&\ddots&\vdots \\ ka_{m1} & ka_{m2}&\cdots&ka_{mn} \\ \end{bmatrix}

수식 : kA=(kann)kA=(ka_{nn})

  • 예시
k=5,A=(1234)k=5, \quad A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\\
kA=5×(1234)=(5×15×25×35×4)=(5101520)kA=5\times\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}=\begin{pmatrix} 5\times1 & 5\times2 \\ 5\times3 & 5\times4 \end{pmatrix}= \begin{pmatrix} 5 & 10 \\ 15 & 20 \end{pmatrix}

🔆 행렬의 곱셈

  • 행렬의 곱하기는 앞의 행렬의 열의 수와 곱해지는 뒤의 행렬의 행의 수가 같을 때만 곱셈 가능(A = m×n, B= n×m)
    • A의 행벡터와 B의 열벡터가 곱해짐
  • 또한 곱셈 결과 나오는 행렬의 크기는 앞의 행렬의 행의 수와 뒤의 행렬의 열의 수로 나옴
A=(a11a12a21a22),B=(b11b12b21b22)A=\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}, \qquad B=\begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}
⇒AB=(a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22)\\\Rightarrow AB=\begin{pmatrix} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \\ \end{pmatrix}
  • 행벡터와 열벡터의 내적을 구한다.
    • 두 행렬의 곱셈 = 각 원소들의 벡터의 내적
a⋅b=(axi^+ayj^+azk^)⋅(bxi^+byj^+bzk^)\large a\cdot b = (\textcolor{red}{a_x}\hat{i}+\textcolor{blue}{a_y}\hat{j}+\textcolor{green}{a_z}\hat{k})\cdot(\textcolor{red}{b_x}\hat{i}+\textcolor{blue}{b_y}\hat{j}+\textcolor{green}{b_z}\hat{k})
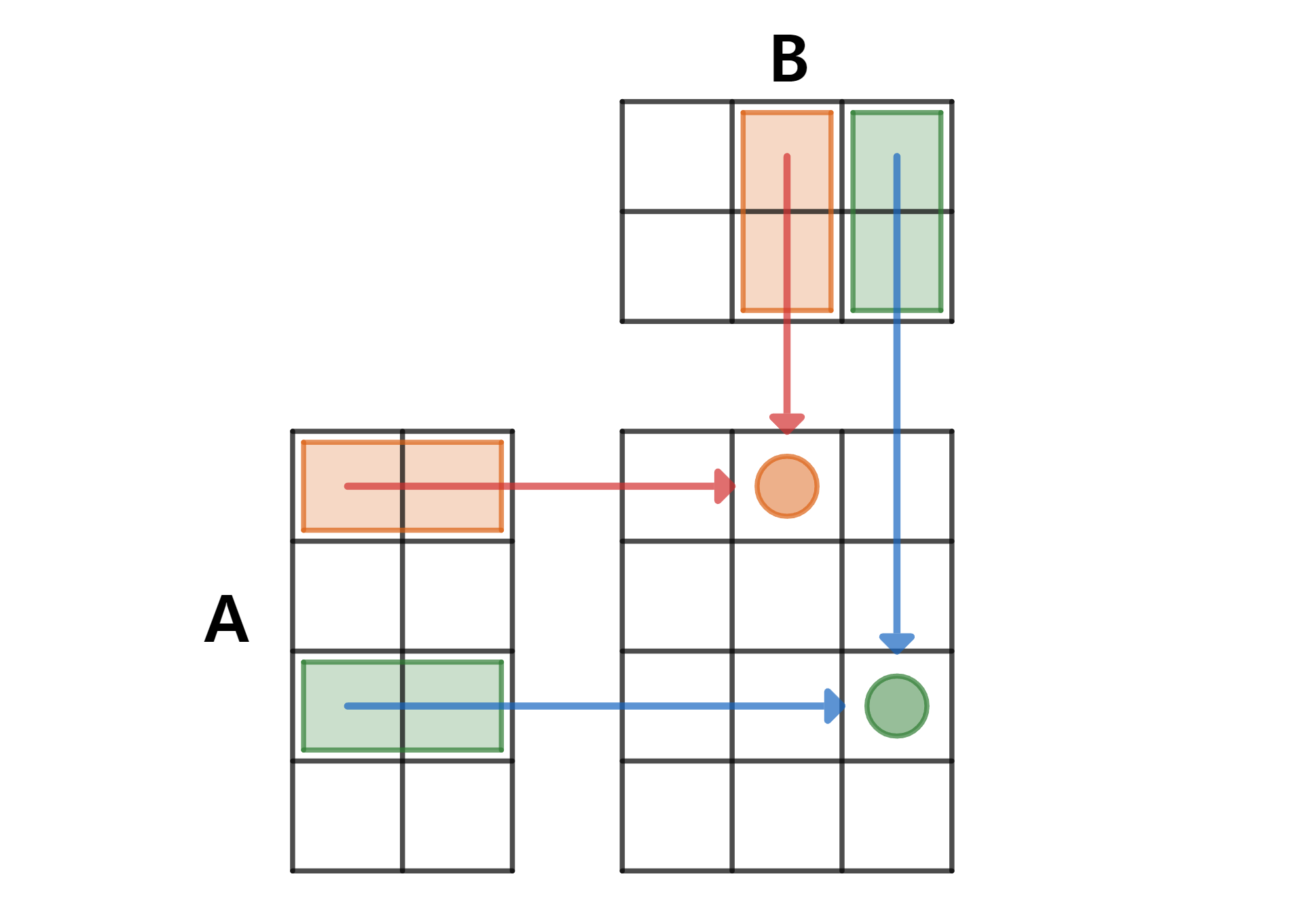
[axayaz][bxbybz]=axbx+ayby+azbz스칼라값들만(크기)\begin{bmatrix} \textcolor{red}{a_x} \\ \textcolor{blue}{a_y} \\ \textcolor{green}{a_z} \\ \end{bmatrix} \begin{bmatrix} \textcolor{red}{b_x} & \textcolor{blue}{b_y} & \textcolor{green}{b_z} \end{bmatrix} \quad = \textcolor{red}{a_xb_x}+\textcolor{blue}{a_yb_y}+\textcolor{green}{a_zb_z}\\ 스칼라 값들만(크기)

A행렬과 B행렬의 각 벡터들의 내적
  • A의 첫번째 행벡터와 B의 첫번째 열 벡터의 내적
A=(a11a12a21a22),B=(b11b12b21b22)A=\begin{pmatrix} \colorbox{#fad3cf}{$a_{11}$} & \colorbox{#fad3cf}{$a_{12}$} \\ a_{21} & a_{22} \end{pmatrix}, \qquad B=\begin{pmatrix} \colorbox{#fad3cf}{$b_{11}$} & b_{12} \\ \colorbox{#fad3cf}{$b_{21}$} & b_{22} \end{pmatrix}
⇒AB=(a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22)\\\Rightarrow AB=\begin{pmatrix} \colorbox{#fad3cf}{$a_{11} b_{11} + a_{12} b_{21}$} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \\ \end{pmatrix}
  • A의 첫번째 행벡터와 B의 두번째 열 벡터의 내적
A=(a11a12a21a22),B=(b11b12b22b22)A=\begin{pmatrix} \colorbox{#d4f1ff}{$a_{11}$} & \colorbox{#d4f1ff}{$a_{12}$} \\ a_{21} & a_{22} \end{pmatrix}, \qquad B=\begin{pmatrix} b_{11}&\colorbox{#d4f1ff}{$b_{12}$} & \\ b_{22} &\colorbox{#d4f1ff}{$b_{22}$} \end{pmatrix}
⇒AB=(a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22)\\\Rightarrow AB=\begin{pmatrix} a_{11} b_{11} + a_{12} b_{21} & \colorbox{#d4f1ff}{$a_{11} b_{12} + a_{12} b_{22}$} \\ a_{21} b_{11} + a_{22} b_{21} & a_{21} b_{12} + a_{22} b_{22} \\ \end{pmatrix}
  • A의 두번째 행벡터와 B의 첫번째 열 벡터의 내적
A=(a11a12a21a22),B=(b11b12b21b22)A=\begin{pmatrix} a_{11} & a_{12}\\ \colorbox{#fff9cf}{$a_{21}$} & \colorbox{#fff9cf}{$a_{22}$} \end{pmatrix}, \qquad B=\begin{pmatrix} \colorbox{#fff9cf}{$b_{11}$} & b_{12} \\ \colorbox{#fff9cf}{$b_{21}$} & b_{22} \end{pmatrix}
⇒AB=(a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22)\\\Rightarrow AB=\begin{pmatrix} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ \colorbox{#fff9cf}{$a_{21} b_{11} + a_{22} b_{21}$} & a_{21} b_{12} + a_{22} b_{22} \\ \end{pmatrix}
  • A의 두번째 행벡터와 B의 두번째 열 벡터의 내적
A=(a11a12a21a22),B=(b11b12b22b22)A=\begin{pmatrix} a_{11} & a_{12}\\ \colorbox{#d0e1d2}{$a_{21}$} & \colorbox{#d0e1d2}{$a_{22}$} \end{pmatrix}, \qquad B=\begin{pmatrix} b_{11}&\colorbox{#d0e1d2}{$b_{12}$} & \\ b_{22} &\colorbox{#d0e1d2}{$b_{22}$} \end{pmatrix}
⇒AB=(a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22)\\\Rightarrow AB=\begin{pmatrix} a_{11} b_{11} + a_{12} b_{21} & a_{11} b_{12} + a_{12} b_{22} \\ a_{21} b_{11} + a_{22} b_{21} & \colorbox{#d0e1d2}{$a_{21} b_{12} + a_{22} b_{22}$} \\ \end{pmatrix}

수식 : (amn)(bnm)=∑kamkbkn(a_{mn})(b_{nm})=\sum_k a_{mk}b_{kn}

  • 예시
    A=(1234),B=(5678)A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix},\quad B=\begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}\\
    ⇒AB=(1×5+2×71×6+2×83×5+4×73×6+4×8)\\\Rightarrow AB=\begin{pmatrix} 1\times5+2\times7 & 1\times6+2\times8 \\ 3\times5+4\times7 & 3\times6+4\times8 \end{pmatrix}
    =(5+146+1615+2818+32)=(19224350)\\= \begin{pmatrix} 5+14 & 6+16 \\ 15+28 & 18+32 \end{pmatrix} =\begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix}

🔆 행렬의 곱하기는 AB ≠ BA

  • AB
    A=(1234),B=(5678)A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix},\quad B=\begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}\\
    ⇒AB=(1×5+2×71×6+2×83×5+4×73×6+4×8)\\\Rightarrow AB=\begin{pmatrix} 1\times5+2\times7 & 1\times6+2\times8 \\ 3\times5+4\times7 & 3\times6+4\times8 \end{pmatrix}\\
    =(5+146+1615+2818+32)=(19224350)=\begin{pmatrix} 5+14 & 6+16 \\ 15+28 & 18+32 \end{pmatrix} =\begin{pmatrix} 19 & 22 \\ 43 & 50 \end{pmatrix}
  • BA
    B=(5678),A=(1234)B=\begin{pmatrix} 5 & 6 \\ 7 & 8 \end{pmatrix}, \quad A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}
    ⇒BA=(5×1+6×35×2+6×47×1+8×37×2+8×4)\\\Rightarrow BA=\begin{pmatrix} 5\times1+6\times3 & 5\times2+6\times4 \\ 7\times1+8\times3 & 7\times2+8\times4 \end{pmatrix}\\
    =(5+1810+247+2414+32)=(23343146)=\begin{pmatrix} 5+18 & 10+24 \\ 7+24 & 14+32 \end{pmatrix} =\begin{pmatrix} 23 & 34 \\ 31 & 46 \end{pmatrix}

🔆 앞의 행렬의 크기[m×n], 뒤 행렬 크기 [n×k]이면 두 행렬을 곱했을 때 [m×k]

C=(12),D=(345678)C=\begin{pmatrix} 1 & 2 \end{pmatrix},\quad D=\begin{pmatrix} 3&4&5\\ 6& 7 & 8 \end{pmatrix}\\
⇒CD=(1×3+2×61×4+2×71×5+2×8)\\\Rightarrow CD=\begin{pmatrix} 1\times3+2\times6 & 1\times4+2\times7 & 1\times5+2\times8 \end{pmatrix}\\
=(3+124+145+16)=(151821)=\begin{pmatrix} 3+12 & 4+14 &5+16 \end{pmatrix} =\begin{pmatrix} 15&18&21 \end{pmatrix}

📖 전치 행렬

🔆 전치 행렬 : 행렬을 뒤집어 놓은 형태

A=[aij]m×n전치행렬AT=[aji]m×nA=[a_{ij}]_{m\times n}\quad 전치 행렬A^T=[a_{ji}]_{m\times n}

  • 행렬의 전치는 대각선으로 접는다.
A=(abcd),AT=(acbd)A=\begin{pmatrix} a & \textcolor{red}{b} \\ \textcolor{red}{c} & d \end{pmatrix},\quad A^T=\begin{pmatrix} a & \textcolor{red}{c} \\ \textcolor{red}{b} & d \end{pmatrix}\\
B=(1234),BT=(1324)B=\begin{pmatrix} 1 & \textcolor{red}{2} \\ \textcolor{red}{3} & 4 \end{pmatrix},\quad B^T=\begin{pmatrix} 1 & \textcolor{red}{3} \\ \textcolor{red}{2} & 4 \end{pmatrix}
- 직사각형 행렬일 경우 - 1번째 기준으로 대각선 긋기

[m×n]T=[n×m][m\times n]^T = [n\times m]

AAAT(AT)T=A[123456]123456135246[123456]\begin{matrix} A & A &A^T&(A^T)^T=A \\ \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5&6 \end{bmatrix} & \boxed{ \begin{matrix} 1 & \textcolor{red}{2} \\ \textcolor{red}{3} & 4 \\ \textcolor{red}{5}&\textcolor{red}{6} \end{matrix}} & \boxed{\begin{matrix} 1 & \textcolor{red}{3}&\textcolor{red}{5} \\ \textcolor{red}{2} & 4 &\textcolor{red}{6} \end{matrix}}& \begin{bmatrix} 1 & \textcolor{red}{2} \\ \textcolor{red}{3} & 4 \\ \textcolor{red}{5}&\textcolor{red}{6} \end{bmatrix} \end{matrix}
  • 예시
E=[12345678]ET=[15263748]F=[123]FT=[123]E=\begin{bmatrix} 1 & \textcolor{red}{2} & \textcolor{red}{3} & \textcolor{red}{4} \\ \textcolor{red}{5} & 6 & \textcolor{red}{7} & \textcolor{red}{8} \end{bmatrix}\qquad E^T=\begin{bmatrix} 1 & \textcolor{red}{5} \\ \textcolor{red}{2} & 6 \\ \textcolor{red}{3} & \textcolor{red}{7} \\ \textcolor{red}{4} & \textcolor{red}{8} \end{bmatrix} \\ F=\begin{bmatrix} 1 \\ \textcolor{red}{2} \\ \textcolor{red}{3} \end{bmatrix}\qquad F^T=\begin{bmatrix} 1 & \textcolor{red}{2} & \textcolor{red}{3} \end{bmatrix}

📖 역행렬

🔆 역행렬

  • A×A−1A \times A^{-1}
    A×A−1=단위행렬[10⋯001⋯0⋮⋮⋱⋮00⋯1]A \times A^{-1}= 단위행렬\begin{bmatrix} 1 & 0&\cdots &0\\ 0 & 1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots \\ 0&0&\cdots&1 \end{bmatrix}
  • [2×2]행렬의 역행렬(암기)
    A−1=[abcd]−1=1ad−bc[d−b−ca]A^{-1}=\begin{bmatrix} \textcolor{red}{a}&\textcolor{blue}{b}\\ \textcolor{blue}{c}&\textcolor{red}{d} \end{bmatrix}^{-1} = \frac 1 {\textcolor{red}{ad}-\textcolor{blue}{bc}} \begin{bmatrix} \textcolor{red}{d} &\textcolor{blue}{-b}\\ \textcolor{blue}{-c} &\textcolor{red}{a} \end{bmatrix}
  • [3×3]행렬의 역행렬 (복잡함)
A−1=[abcdefghi]−1A^{-1}=\begin{bmatrix} a&b&c\\ d&e&f\\ g&h&i \end{bmatrix}^{-1}
=1∣A∣[ei−fh−(bi−ch)bf−ce−(di−fg)ai−cg−(af−cd)dh−eg−(ah−bg)ae−bd]\\= \frac 1 {|A|} \begin{bmatrix} ei-fh&-(bi-ch)&bf-ce \\ -(di-fg)&ai-cg&-(af-cd)\\ dh-eg&-(ah-bg)&ae-bd \end{bmatrix}
=1∣A∣[ei−fhch−bibf−cefg−diai−cg−cd−afdh−egbg−ahae−bd]\\= \frac 1 {|A|} \begin{bmatrix} ei-fh&ch-bi&bf-ce \\ fg-di&ai-cg&-cd-af\\ dh-eg&bg-ah&ae-bd \end{bmatrix}
∣A∣=a(ei−fh)−b(di−fg)+c(dh−eg)=−d(bi−ch)+e(ai−cg)−f(ah−bg)=g(bf−ce)−h(af−cd)+i(ae−bd)|A|= a(ei-fh)-b(di-fg)+c(dh-eg)\\ = -d(bi-ch)+e(ai-cg)-f(ah-bg)\\ = g(bf-ce)-h(af-cd)+i(ae-bd)
profile
yeppi1802
제로베이스 DA7 김예빈입니다.
이전 포스트

선형대수 : 02 행렬 - 1 : 행렬의 정의

다음 포스트

선형대수 : 02 행렬 - 3 : 기타 특수 행렬

0개의 댓글