선형대수 : 03 선형대수학 - 1 : 선형 방정식 소개

yeppi1802·2024년 6월 26일
선형대수제로베이스
0

선형대수_제로베이스 데이터 분석 스쿨

목록 보기
6/12

❇️ 요약

  • 선형 방정식
  • 선형 방정식 계 / 해의 집합 / 상등
  • No solution / Exactly One Solution / Infinitely Many Solution
  • 행렬 표기법 / 계수 행렬 / 첨가 행렬

📖 선형 방정식

🔆 선형 방정식 소개

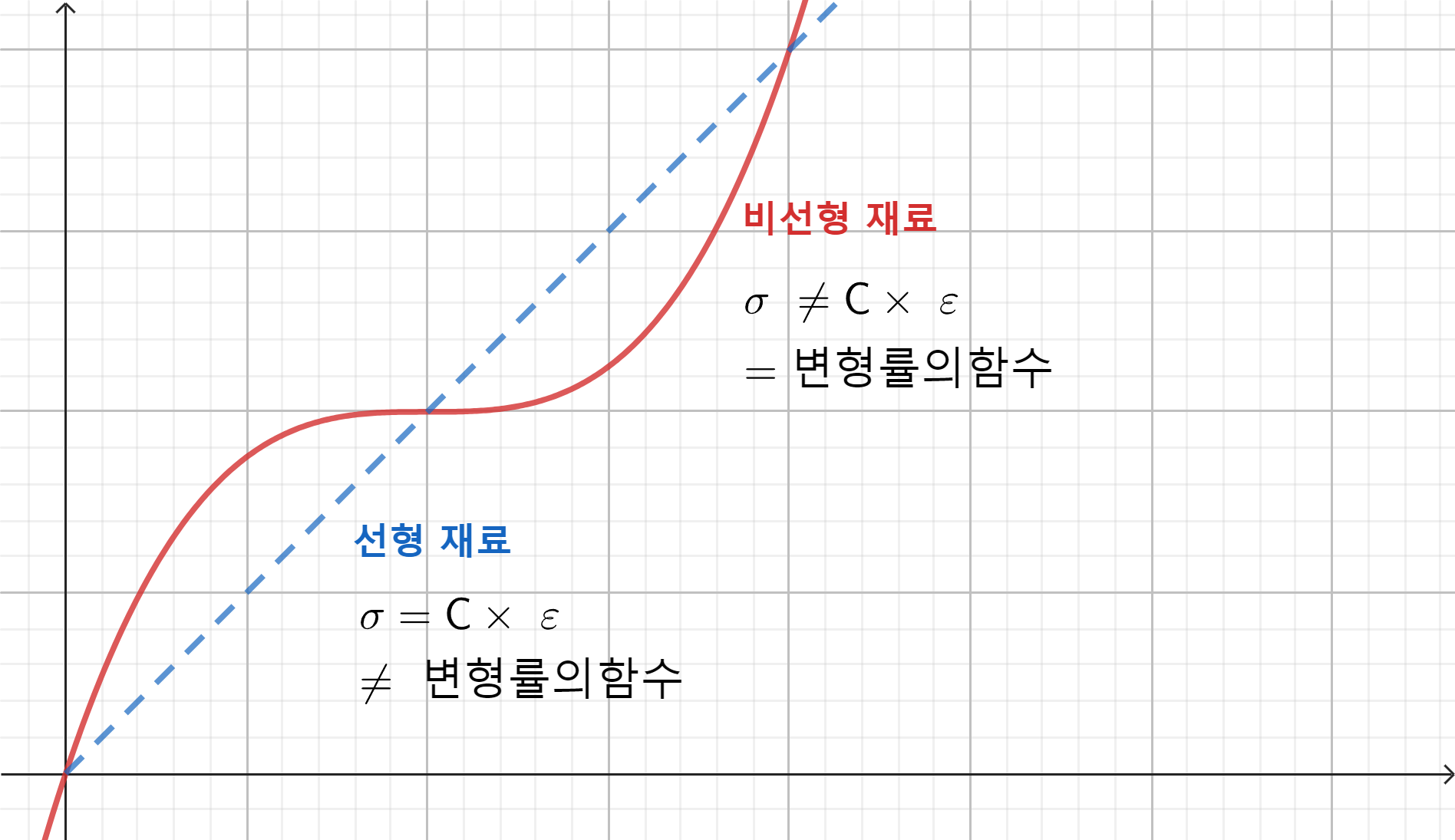
  • 선형 방정식 : linear equation
a1x1+a2x2+...+anxn=ba_1x_1 + a_2x_2+...+a_nx_n=b

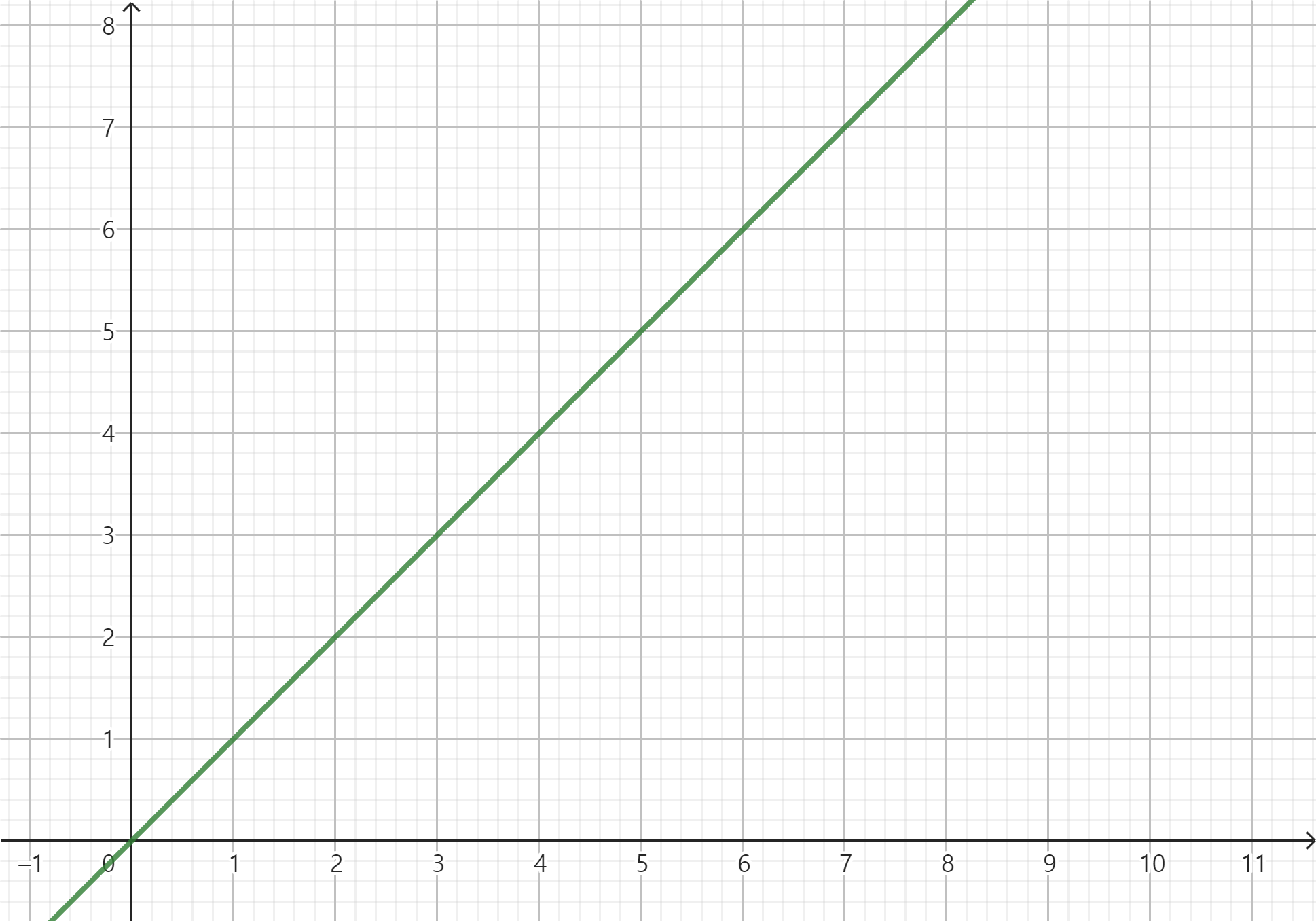
  • 비선형 방정식 : nonlinear equation
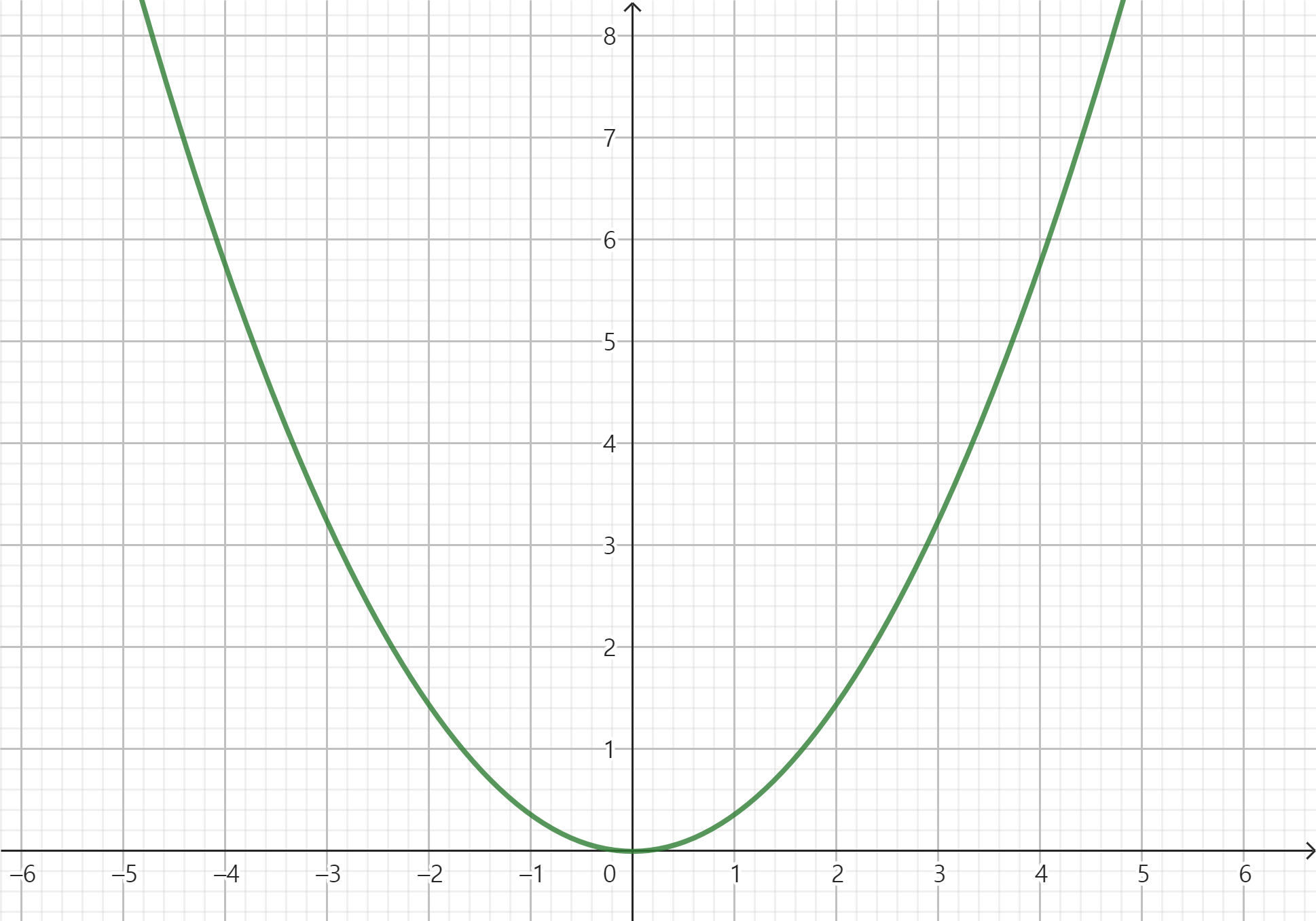
4x1−5x2=x1x2  and  x2=2x2−64x_1-5x_2=\textcolor{red}{x_1x_2}\;and\;x_2=2\textcolor{red}{\sqrt{x_2}}-6

📖 선형 방정식 계

🔆 선형 방정식 계 : A system of linear equation

  • 선형 방정식 계(A system of linear equation)는 선형 시스템(linear system)이라는 용어를 사용함
  • 선형 방정식 계는 같은 변수들을 포함한 선형 방정식이 1개 또는 그 이상의 집합을 의미함
  • 아래 두 개의 선형 방정식은 선형 방정식 계라고 할 수 있음
2x1−x2+1.5x3=8x1−4x3=−7\begin{aligned} 2x_1-x_2+1.5x_3&=8\\ x_1-4x_3&=-7 \end{aligned}
  • 행렬로 표현
[2−11.510−4][x1x2x3]=[8−7]\begin{bmatrix} 2&-1&1.5 \\ 1&0&-4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 8 \\ -7 \end{bmatrix}

🔆 해의 집합 : Solution set

  • Solution set은 선형 시스템에서 모든 가능한 해의 집합을 의미함

🔆 상등 : Equivalent

  • 두 선형 시스템이 같은 Solution set을 갖고 있다면 두 선형 시스템은 상등(equivalent)하다고 함
  • 즉, 같은 solution set을 갖는 선형 방정식 간의 관계를 행 상등(equivalent)라고 함

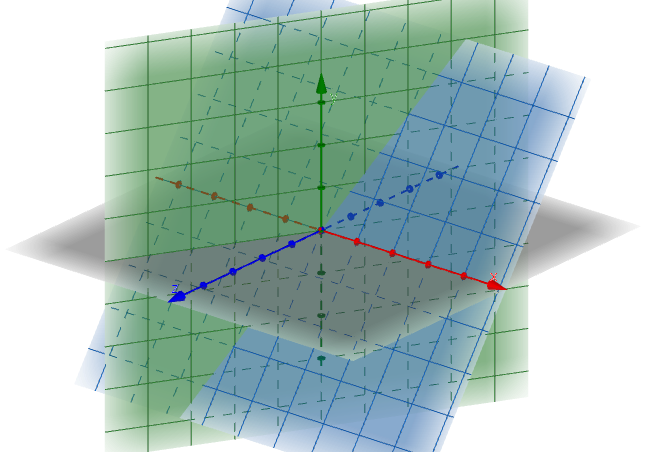
🔆 선형 방정식 계 - 1. no solution, 2. exactly one solution, 3. infinitely many solution

  • Inconsistent : 1. No Solution를 의미
  • consistent : 2. Exactly One Solution, 3. Infinitely Many Solution를 의미

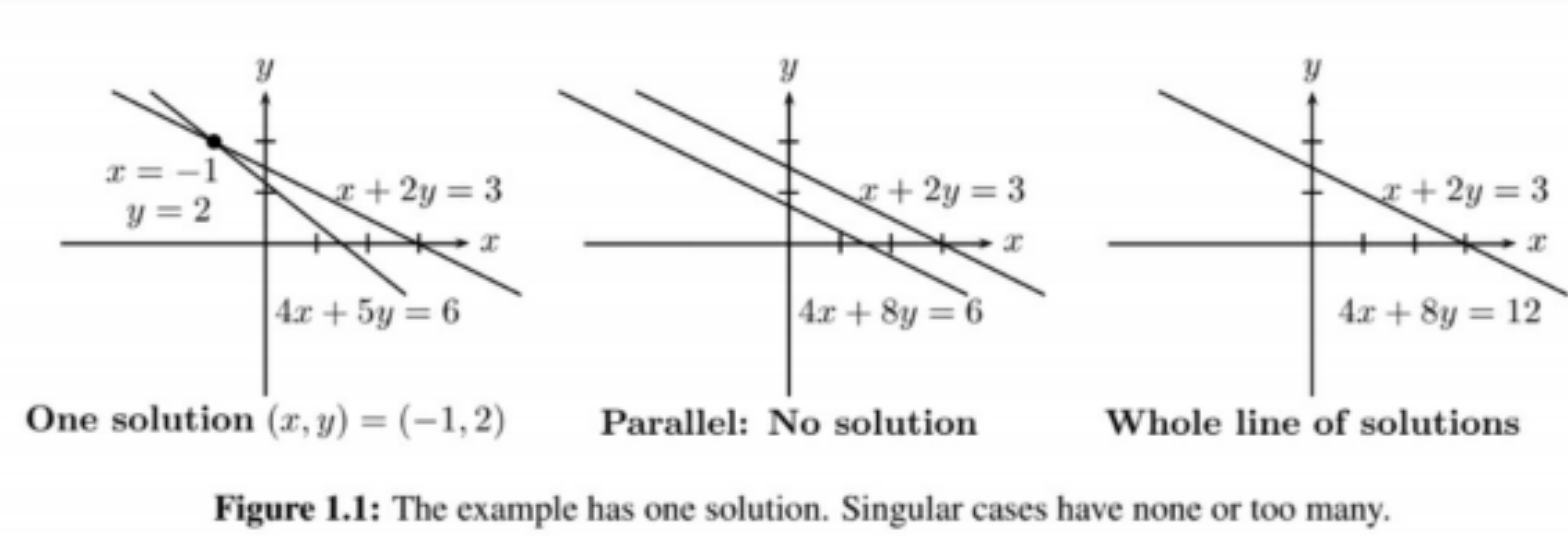
  • 해가 없다(Inconsistent)

    x1−2x2=−1−x1+2x2=3\begin{aligned} x_1-2x_2&=-1\\ -x_1+2x_2&=3 \end{aligned}

  • 해가 하나인 경우(Exactly One Solution)

    x1−2x2=−1−x1+3x2=3\begin{aligned} x_1-2x_2&=-1\\ -x_1+3x_2&=3 \end{aligned}

  • 해가 무수히 많은 경우(Infinitely Many Solution)

    x1−2x2=−1−x1+2x2=1\begin{aligned} x_1-2x_2&=-1\\ -x_1+2x_2&=1 \end{aligned}

  • 2개의 해가 존재하는 경우는? - 비선형인 경우

📖 행렬 표기법

🔆 행렬 표기법 matrix notation

  • 행렬 표기법은 선형 시스템을 행렬로 표현한 것
a          bx1−2x2+x3=02x2−8x3=85x1−5x3=10\begin{aligned} a\qquad\quad\qquad&\;\;\;\;\;b\\ x_1-2x_2+x_3&=0\\ 2x_2-8x_3&=8\\ 5x_1-5x_3&=10 \end{aligned}

🔆 계수 행렬 : coefficient matrix

  • 계수 행렬은 b를 제외하고 a만을 행렬로 나타낸 것
[1−2102−850−5]\begin{bmatrix} 1&-2&1 \\ 0&2&-8 \\ 5&0&-5 \end{bmatrix}

🔆 첨가 행렬 : augmented matrix

  • 첨가 행렬은 b까지 포함한 행렬
[1−21002−8850−510]\begin{bmatrix} 1&-2&1&0 \\ 0&2&-8&8 \\ 5&0&-5&10 \end{bmatrix}
profile
yeppi1802
제로베이스 DA7 김예빈입니다.
이전 포스트

선형대수 : 02 행렬 - 3 : 기타 특수 행렬

다음 포스트

선형대수 : 03 선형대수학 - 2 : 소거법(elimination)

0개의 댓글