선형대수 : 03 선형대수학 - 2 : 소거법(elimination)

yeppi1802·2024년 6월 26일
선형대수제로베이스
0

선형대수_제로베이스 데이터 분석 스쿨

목록 보기
7/12

❇️ 요약

  • 선형방정식의 n=2일때 행관점과 열관점
  • 선형방정식의 n=3일때 행관점과 열관점
  • 가우스 소거법

📖 선형방정식의 n=2일때 행관점과 열관점 (변수가 2개 일때)

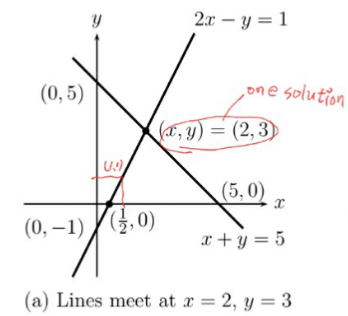
🔆 행(rows) 관점으로 선형 방정식 접근

  • 두 개의 식이 X, Y 좌표에 표시 가능
  • 두 식이 교차하는 (2,3)에서 해(solution)이 존재
  • x=2, y=3
2x−y=1x+y=5[2−111][xy]=[15]3x=6x=2,y=3\begin{aligned} 2x-y&=1 \\ x+y&=5 \end{aligned} \qquad \begin{bmatrix} 2&-1 \\ 1&1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \end{bmatrix} \qquad 3x = 6\quad x=2, y=3

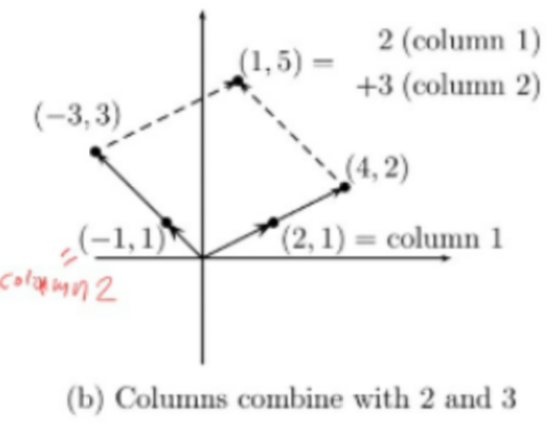
🔆 열(column) 관점으로 선형 방정식 접근

  • (2,1)(2, 1) Vector에 2(x)2(x)를 곱하고 (−1,1)(-1, 1) Vector에 3(y)3(y)를 곱함
    • 상수배를 곱하여 값을 구함
  • 위와 같이 곱하게 되면 (4,2)+(−3,3)=(1,5)(4, 2) + (-3, 3) = (1, 5) 가 됨
  • 벡터들을 어디까지 늘려야 결과점에 도달할 수 있는지
2x−y=1x+y=5\begin{aligned} 2x-y&=1 \\ x+y&=5 \end{aligned}
Column formx[21]+y[−11]=[15]\text{Column form}\quad x\begin{bmatrix} 2 \\ 1 \end{bmatrix} + y\begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 5 \end{bmatrix}

📖 선형방정식의 n = 3일 때 행관점과 열관점 (변수가 3개일 때)

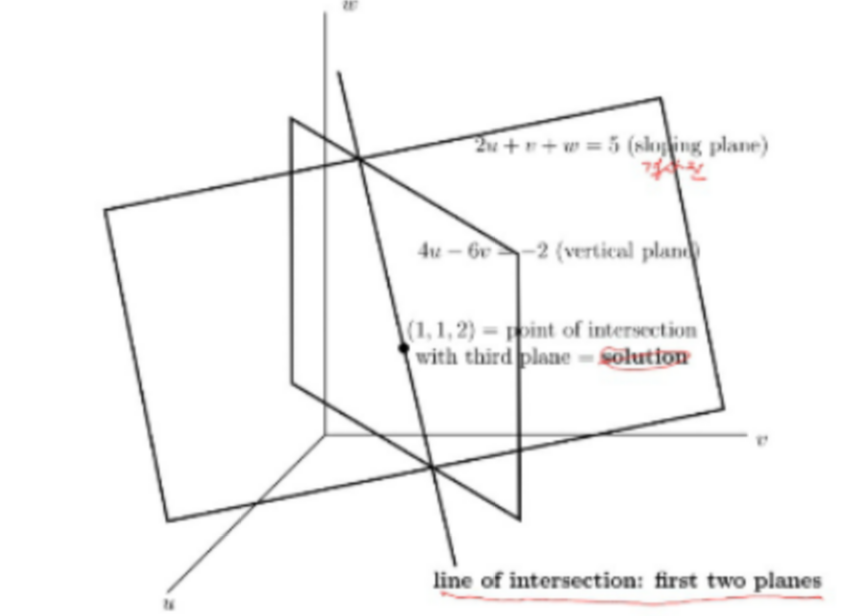
🔆 행(row) 관점으로 선형 방정식 접근

2u+v+w=54u−6v=−2−2u+7v+2w=9[211460−272][uvw]=[5−29]\begin{aligned} 2u&+v&+w&=5 \\ 4u&-6v&&=-2\\ -2u&+7v&+2w&=9 \end{aligned} \qquad \begin{bmatrix} 2&1&1 \\ 4&6&0\\ -2&7&2 \end{bmatrix} \begin{bmatrix} u \\ v\\ w \end{bmatrix} = \begin{bmatrix} 5 \\ -2\\ 9 \end{bmatrix}

🔆 열(column) 관점으로 선형 방정식 접근

  • 벡터의 상수배의 조합으로 해를 찾을 수 있다.
Three planes2u+v+w=54u−6v=−2−2u+7v+2w=9\text{Three planes}\quad \begin{aligned} 2u&+v&+w&=5 \\ 4u&-6v&&=-2\\ -2u&+7v&+2w&=9 \end{aligned}
Column formu[24−2]+v[1−67]+w[102]=[5−29]=b\text{Column form}\quad u\begin{bmatrix} 2 \\ 4 \\ -2 \end{bmatrix} + v\begin{bmatrix} 1 \\ -6 \\ 7 \end{bmatrix} + w\begin{bmatrix} 1 \\ 0\\ 2 \end{bmatrix} = \begin{bmatrix} 5 \\ -2\\ 9 \end{bmatrix} =b
  • 벡터 덧셈 - Vector addition
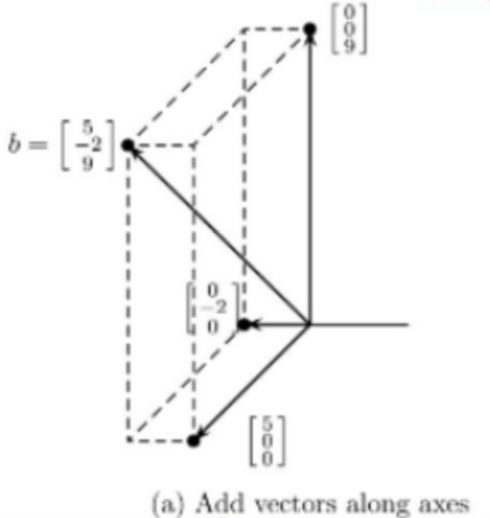
    Vector addtion[500]+[0−20]+[009]=[5−29]\text{Vector addtion}\quad \begin{bmatrix} 5 \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ -2 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0\\ 9 \end{bmatrix} = \begin{bmatrix} 5 \\ -2\\ 9 \end{bmatrix}
  • 벡터 곱셈 - Multiplication by scalars
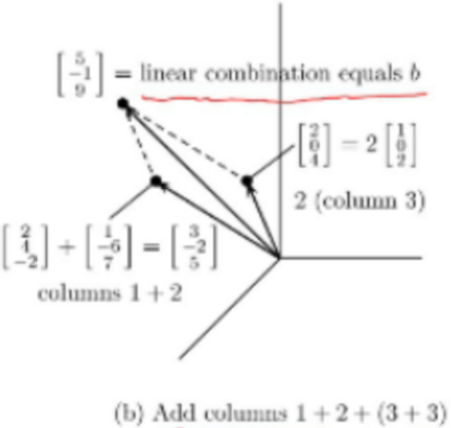
    Multiplication by scalars2[102]=[204],−2[102]=[−20−4]\text{Multiplication by scalars}\quad 2\begin{bmatrix} 1 \\ 0 \\ 2 \end{bmatrix} = \begin{bmatrix} 2 \\ 0 \\ 4 \end{bmatrix}, \qquad -2\begin{bmatrix} 1 \\ 0 \\ 2 \end{bmatrix} = \begin{bmatrix} -2 \\ 0 \\ -4 \end{bmatrix}
  • 선형 결합 - Linear combination

    • 벡터의 곱셈과 덧셈의 결과를 선형 결합(linear combination)이라고 함

    • 오른쪽 항인 b를 만들기 위해서 u=1, v=1, w=2가 필요

    • row picture에서 3개의 평면들의 교차점(1, 1, 2)로 나타낼 수 있다.

      Linear combination1[24−2]+1[1−67]+2[102]=[5−29]\text{Linear combination}\quad \bold{1}\begin{bmatrix} 2 \\ 4 \\ -2 \end{bmatrix} + \bold{1}\begin{bmatrix} 1 \\ -6 \\ 7 \end{bmatrix} + \bold{2}\begin{bmatrix} 1 \\ 0\\ 2 \end{bmatrix} = \begin{bmatrix} 5 \\ -2\\ 9 \end{bmatrix}

📖 행관점과 열관점

  • Row picture (행관점) : 평면들의 교차점(intersection of plans)
  • Column picture (열관점) : 열들의 결합(Combination of columns)

📖 소거법(Elimination)

🔆 소거법

  • 행 연산(row operation)을 통해 소거법(elimination)을 진행하고 선형 방정식(linear equation)의 해(Solution)을 구할 수 있음

  • 가우스 소거법에서 행할 수 있는 기본 행 연산(elementary row operations)

    1. 0이 아닌 상수를 행에 곱할 수 있다. (scaling)
    2. 두 행을 교환할 수 있다. (interchange)
    3. 한 행을 상수배 하여 다른 행에 더할 수 있다. (replacement)

  • 상/하삼각행렬을 만들어 해를 찾음

  • 예시

    {x−2y=13x+2y=11\begin{cases} \begin{aligned} x-2y&=1\\ 3x+2y&=11 \end{aligned} \end{cases}
    • 첫번째 행에 (-3) 곱함 : 0이 아닌 상수를 행에 곱할 수 있다.
      {−3x+6y=−33x+2y=11\begin{cases} \begin{aligned} -3x+6y&=-3\\ 3x+2y&=11 \end{aligned} \end{cases}
    • 첫번째 행을 두번째 행에 더함 : 한 행을 상수배 하여 다른 행에 더할 수 있다.
      {−3x+6y=−38y=8\begin{cases} \begin{aligned} -3x+6y&=-3\\ 8y&=8 \end{aligned} \end{cases}

📖 가우스 소거법

🔆 1. 선형 방정식 계를 행렬로 표현함

  • b가 포함되어 있는 첨가 행렬
x1−2x2+x3=02x2−8x3=85x1−5x3=10[1−21002−8850−510]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\quad2x_2&-8x_3&=8\\ 5x_1&&-5x_3&=10 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&2&-8&8\\ 5&0&-5&10 \end{bmatrix}

🔆 2. 마지막 행의 x1x_1의 계수를 0으로 만듦

  • 1번째 식에 -5를 곱함
  • 1번째 식과 3번째 식을 더함
−5⋅[equation 1]+[equation 3][new equation 3]−5x1+10x2−5x3=05x1−5x3=10    10x2−10x3=10\frac {\begin{aligned} -5\cdot[\text{equation 1}]\\ +[\text{equation 3}] \end{aligned}}{[\text{new equation 3}]} \qquad\qquad \frac { \begin{aligned} -5x_1&+10x_2&-5x_3&=0\\ 5x_1&&-5x_3&=10 \end{aligned} }{ \begin{aligned} \qquad\;\;\quad10x_2&-10x_3=10 \end{aligned} }
  • 행렬 업데이트
x1−2x2+x3=02x2−8x3=810x2−10x3=10[1−21002−88010−1010]\begin{aligned} x_1-2x_2+x_3&=0\\ 2x_2-8x_3&=8\\ 10x_2-10x_3&=10 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&2&-8&8\\ 0&10&-10&10 \end{bmatrix}

🔆 3. 마지막 행의 x2x_2의 계수를 0으로 만듦

x1−2x2+x3=0x2−4x3=410x2−10x3=10[1−21001−44010−1010]\begin{aligned} x_1-2x_2+x_3&=0\\ x_2-4x_3&=4\\ 10x_2-10x_3&=10 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&1&-4&4\\ 0&10&-10&10 \end{bmatrix}
  • 2번째 식에 -10을 곱하고 3번째 식과 더함
−10⋅[equation 2]+[equation 3][new equation 3]−10x2+40x3=−4010x1−10x3=1030x3=−30\frac {\begin{aligned} -10\cdot[\text{equation 2}]\\ +[\text{equation 3}] \end{aligned}}{[\text{new equation 3}]} \qquad\qquad \frac { \begin{aligned} &-10x_2&+40x_3&=-40\\ 10x_1&&-10x_3&=10 \end{aligned} }{ \begin{aligned} \qquad\qquad\qquad\quad30x_3&=-30 \end{aligned} }
  • 행렬 업데이트
x1−2x2+x3=0x2−4x3=430x3=−30[1−21001−440030−30]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\qquad x_2&-4x_3&=4\\ &&30x_3&=-30 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&1&-4&4\\ 0&0&30&-30 \end{bmatrix}

🔆 4. 마지막 행의 x3x_3의 계수를 1로 만듦

  • 상삼각행렬 완성!
x1−2x2+x3=0x2−4x3=430x3=−30[1−21001−440030−30]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\qquad x_2&-4x_3&=4\\ &&30x_3&=-30 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&1&-4&4\\ 0&0&30&-30 \end{bmatrix}
  • 3번째 식에 30을 나눔
x1−2x2+x3=0x2−4x3=4x3=−1[1−21001−44001−1]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\qquad x_2&-4x_3&=4\\ &&x_3&=-1 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&1&-4&4\\ 0&0&1&-1 \end{bmatrix}

🔆 5. x3x_3을 알았으므로 대입을 통해 x1x_1, x2x_2를 구할 수 있음

x1−2x2+x3=0x2−4x3=4x3=−1[1−21001−44001−1]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\qquad x_2&-4x_3&=4\\ &&x_3&=-1 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&1&-4&4\\ 0&0&1&-1 \end{bmatrix}
4⋅[equation 3]+[equation 2][new equation 2]4x3=−4x2−4x3=4x2=0\frac {\begin{aligned} 4\cdot[\text{equation 3}]\\ +[\text{equation 2}] \end{aligned}}{[\text{new equation 2}]} \qquad\qquad \frac { \begin{aligned} 4x_3&=-4\\ x_2-4x_3&=4 \end{aligned} }{ \begin{aligned} x_2&&&&&&=0 \end{aligned} }
−1⋅[equation 3]+[equation 1][new equation 1]−x3=1x1−2x2+x3=0x1−2x2=1\frac {\begin{aligned} -1\cdot[\text{equation 3}]\\ +[\text{equation 1}] \end{aligned}}{[\text{new equation 1}]} \qquad\qquad \frac { \begin{aligned} -x_3&=1\\ x_1-2x_2+x_3&=0 \end{aligned} }{ \begin{aligned} x_1&-&2x_2&&&&=1 \end{aligned} }
x1−2x2=1x2=0x3=−1[1−2010100001−1]\begin{aligned} x_1&-2x_2&&=1\\ &\qquad x_2&&=0\\ &&x_3&=-1 \end{aligned} \qquad \begin{bmatrix} 1&-2&0&1\\ 0&1&0&0\\ 0&0&1&-1 \end{bmatrix}
x1=1x2=0x3=−1[10010100001−1]\begin{aligned} x_1&&&=1\\ &x_2&&=0\\ &&x_3&=-1 \end{aligned} \qquad \begin{bmatrix} 1&0&0&1\\ 0&1&0&0\\ 0&0&1&-1 \end{bmatrix}

🔆 x1=1,x2=0,x3=−1x_1 = 1, x_2 = 0, x_3=-1

x1−2x2+x3=02x2−8x3=85x1−5x3=10[1−21002−8850−510]\begin{aligned} x_1&-2x_2&+x_3&=0\\ &\quad 2x_2&-8x_3&=8\\ 5x_1&&-5x_3&=10 \end{aligned} \qquad \begin{bmatrix} 1&-2&1&0\\ 0&2&-8&8\\ 5&0&-5&10 \end{bmatrix}\\
  • 결과
⇓x1=1x2=0x3=−1[10010100001−1]\Darr \\ \begin{aligned} x_1&&&=1\\ &x_2&&=0\\ &&x_3&=-1 \end{aligned} \qquad \begin{bmatrix} 1&0&0&1\\ 0&1&0&0\\ 0&0&1&-1 \end{bmatrix}

🔆 행 상등

  • 행 연산 과정이 하나의 행렬을 다른 행렬로 변환 된다면 두 행렬은 행 상등(row equivalent)하다고 할 수 있음
  • 두 선형 시스템이 행 상등하다면 두 시스템은 동일한 해의 집합을 가지고 있음

ex ) 가우스 소거법

profile
yeppi1802
제로베이스 DA7 김예빈입니다.
이전 포스트

선형대수 : 03 선형대수학 - 1 : 선형 방정식 소개

다음 포스트

선형대수 : 03 선형대수학 - 3 : 선형 방정식의 특이한 경우

0개의 댓글