선형대수 : 03 선형대수학 - 3 : 선형 방정식의 특이한 경우

❇️ 요약

• 특이한 경우 - The Singular Case
• 시스템이 특이할 때, column picture

📖 특이한 경우 - The Singular Case

• 3개의 평면이 한 점에서 교차하지 않을 때 특이한 경우(The SIngular Case)
• 그 경우 해가 없거나 해가 무수히 많게 됨

🔆 1. 해가 없는 경우 (no solution)

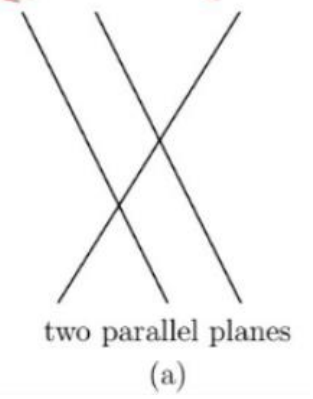
• 3개의 평면은 한 점에서 교차하지 않는다
• 두 개의 평면이 평행하기 때문

🔆 2. 해가 없는 경우 (no solution)

• 모든 한 쌍의 평면이 직선으로 교차
• 교차한 직선들은 모두 평행

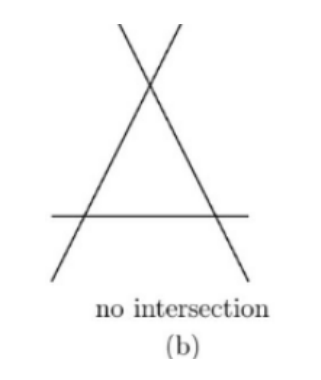
• 1번째 식과 2번째 식을 더했을 때 b가 6이 안됨

🔆 3. 세 개의 평면이 평행한 경우

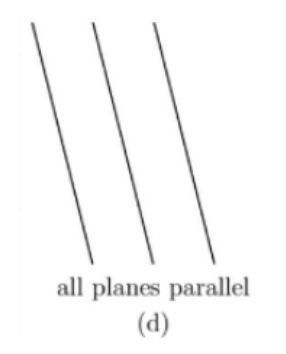
🔆 4. 해가 무수히 많은 경우(infinity of solution)

• 세 평면의 교차로가 하나의 직선이 됨
• 그림은 겹친 평면을 위에서 본 시점

• 3개의 방정식의 결합은 0이 됨

---

📖 시스템이 특이할 때, column picture

🔆 1. 해가 없는 경우 (no solution)

• 세 개의 column이 동일한 평면에 놓이고 b는 다른 평면에 위치 할때 해가 없음

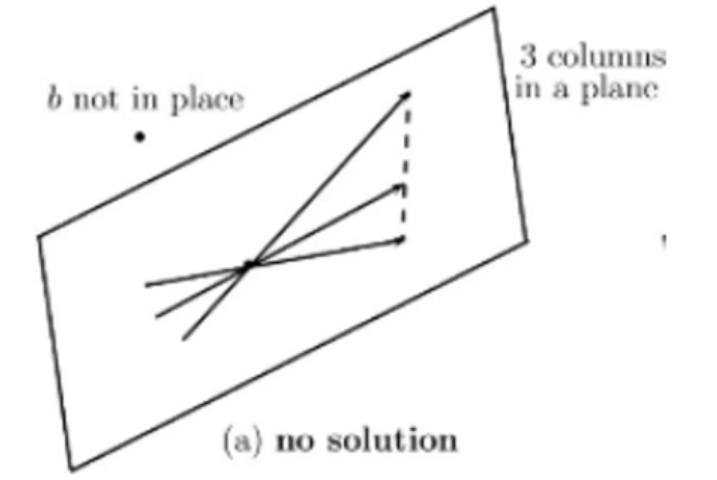
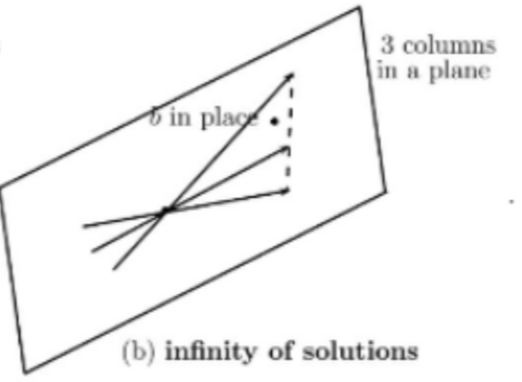
🔆 2. 해가 무수히 많은 경우(infinitely many solutions)

• b가 3개의 열들과 동일한 평면에 놓여져 있을 때 해는 무수히 많게 됨
• b를 만들기 위해 3개의 열들은 무수히 많은 방법으로 결합 가능

🔆 3. 3개의 열들이 동일한 평면에 있는지 알 수 있는 방법

• 합이 0이 되는 열들의 결합을 찾는 것
• 만약 n개의 평면에서 교차점이 없거나 무수히 많은 점이 있다면 n개의 열들은 동일한 평면에 놓여져 있는 것

• 여기서 u=3, v=1, w = -2일 때 선형결합의 합은 0
• 1열은 열2와 열3의 평면에 놓여있음