선형대수 : 03 선형대수학 - 5 : LU 분해(LU decomposition)⭐

yeppi1802·2024년 7월 2일
선형대수제로베이스
0

선형대수_제로베이스 데이터 분석 스쿨

목록 보기
10/12

❇️ 요약

  • LU 분해(LU decomposition)
  • LU 분해 공식

📖 LU 분해(LU decomposition)

🔆 1. 분해 - Factorization, decomposition

  • 분해는 하나의 행렬을 2개 혹은 3개 이상의 행렬 곱으로 표현한 식을 의미
  • AA 행렬을 BB와 CC의 곱으로 표현했는데 이런 형태를 분해(factorization)이라고 함
A=BCA=BC

🔆 2. LU 분해 - LU decomposition

Ax=b1,Ax=b2,⋯ ,Ax=bpA\text{x} =b_1, \quad A\text{x} =b_2,\quad \cdots,\quad A\text{x} =b_p
  • 방정식을 푸는 방식은 크게 두가지

  1. AA의 역행렬을 이용

    • A−1b1,    A−1b2A^{-1}b_1,\;\;A^{-1}b_2 모든 경우를 구해야 하므로 비효율적임

  2. LU 분해⭐⭐⭐

    • 행 줄임(row reduction)으로 AA를 LU분해하여 방정식을 푸는 것이 효과적
    A=[1000∗100∗∗10∗∗∗1][■∗∗∗∗0■∗∗∗000■∗00000]L      UFIGURE   1    An LU factorization\begin{aligned} A=& \begin{bmatrix} 1&0&0&0\\ *&1&0&0\\ *&*&1&0\\ *&*&*&1 \end{bmatrix} \begin{bmatrix} ■&*&*&*&*\\ 0&■&*&*&*\\ 0&0&0&■&*\\ 0&0&0&0&0 \end{bmatrix}\\ &\qquad\quad L\qquad\qquad\qquad\;\;\; U \end{aligned} \\ \textsf{FIGURE \;1}\text{\;\; An LU factorization}
    • LL은 a unit triangular matrix(하삼각행렬)를 의미
    • UU는 echelon form(행사다리꼴)을 의미
    • ❗주의할 점 : U는 reduced echelon form이 아님

    echelon form(행사다리꼴)이란?

    [■∗∗∗∗0■∗∗∗000■∗00000]\begin{bmatrix} ■&*&*&*&*\\ 0&■&*&*&*\\ 0&0&0&■&*\\ 0&0&0&0&0 \end{bmatrix}
    • 한 matrix의 대각선을 기준으로 위쪽에 0이 아닌 값들이 존재하고 그 아래는 모두 0이어서 값이 있는 곳들을 보면 사다리꼴 모양인 matrix
    • ■표시된 부분은 0이 아닌 값이 열을 기준으로 처음 나오는 값
    • 이 ■를 포함하는 열(column)을 leading entry
    • * 또한 0이 아닌 값

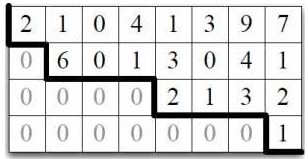
    특징

    • row를 기준으로 모든 element가 0인 row는 모든 element가 0이 아닌 row보다 아래에 있어야 한다.
    • 각각의 leading entry들은 위의 row의 leading entry보다 오른쪽에 위치해야 한다.
    • 각각의 leading entry column은 ∎아래의 element는 0이어야 한다.

    여기서 leading entry에서 column의 첫번째 값을 제외하고는 0이 되어야 함

    그리고 첫번째 값이 1이 되어야 함. 그래야 우리가 해석하기가 쉬워짐

    • A를 분해해서 U로 변환할 때 row interchange, scaling 없이 replacement만을 이용해서 변환 해야함

    • L은 diagonal term이 모두 1이고 아래는 nonzero entry인 행렬임

    • nonzero entry에 zero가 들어가도 상관 없음

    • diagonal term이 모두 1이어야만 하는 이유 : 대각선이 1이 아니면 너무 다양하기 때문

🔆 3. LU 분해의 유용성

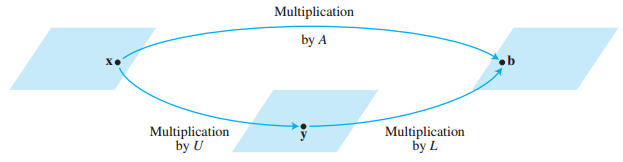
  • A=LUA = LU로 분해하였을 때 Ax=bA\text{x}=b 방정식을 다음과 같이 표현 가능
A=LUAx=bA=LU\\ A\text{x}=b
  • Ux=y\bold {U\bold{x}=y}로 치환하여 대입 → Ly=b\bold {L\text{y}=b}에서 y\bold y를 품
    • Ux=yU\text{x}=y, UU와 yy를 알고있으므로 xx를 풀 수 있음
LUx=bLy=bLU\text{x}=b\\ L\text{y}=b
  • LL과 UU는 pivot을 사용해서 나머지 entry를 0으로 만들 수 있는 쉬운 형태로 이루어져 있기 때문에 빠르게 문제를 풀 수 있다.

🔆 4. LU 분해 예시 문제

[참고 - 선형대수 : 02 행렬 - 3 : 기타 특수 행렬 중 삼각행렬]

  • A=LU→Ax=b→LUx=b→Ux=y(치환)→Ly=b→Ux=y→x의해를찾음\color{tomato} A=LU \rarr A\text{x}=b \rarr \textcolor{blue}{LU\text{x}=b}\rarr U\text{x}=y(치환)\rarr Ly=b \rarr U\text{x}=y \rarr x의 해를 찾음
A=[3−7−22−35106−40−5−95−512]=[1000−11002−510−3831][3−7−220−2−1200−11000−1]=LU\begin{aligned} A=& \begin{bmatrix} 3&-7&-2&2\\ -3&5&1&0\\ 6&-4&0&-5\\ -9&5&-5&12 \end{bmatrix} =\begin{bmatrix} 1&0&0&0\\ -1&1&0&0\\ 2&-5&1&0\\ -3&8&3&1 \end{bmatrix} \begin{bmatrix} 3&-7&-2&2\\ 0&-2&-1&2\\ 0&0&-1&1\\ 0&0&0&-1 \end{bmatrix} =LU \end{aligned}
Ax=b,    where b=[−95711]\begin{aligned} A\text{x}=b,\;\; \text{where }b=& \begin{bmatrix} -9\\ 5\\ 7\\ 11 \end{bmatrix} \end{aligned}
Ux=yLUxb[1000−11002−510−3831][3−7−220−2−1200−11000−1][x1x2x3x4]=[−95711]\begin{aligned} U\text{x}=y\qquad\\ L\qquad\qquad\qquad\quad U\qquad \qquad \quad x\quad &\qquad b\\ \begin{bmatrix} 1&0&0&0\\ -1&1&0&0\\ 2&-5&1&0\\ -3&8&3&1 \end{bmatrix} \begin{bmatrix} 3&-7&-2&2\\ 0&-2&-1&2\\ 0&0&-1&1\\ 0&0&0&-1 \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\x_4 \end{bmatrix} &=\begin{bmatrix} -9\\ 5\\ 7\\ 11 \end{bmatrix} \end{aligned}
  • AA와 bb가 주어졌을 때 우선 Ly=bL\text{y}=b로 yy를 구한다.
[Lb]=([L][y1y2y3y4]=[−95711])=[1000−9−110052−5107−383111]∼[1000−90100−40010500011]=[Iy][L\quad \bold{b}] = \begin{pmatrix} \begin{bmatrix} \\&L&\\\\ \end{bmatrix} \begin{bmatrix} y_1\\y_2\\y_3\\y_4 \end{bmatrix} =\begin{bmatrix} -9\\5\\7\\11 \end{bmatrix} \end{pmatrix} =\begin{bmatrix} 1&0&0&0&-9\\ -1&1&0&0&5\\ 2&-5&1&0&7\\ -3&8&3&1&11 \end{bmatrix} \sim \begin{bmatrix} 1&0&0&0&-9\\ 0&1&0&0&-4\\ 0&0&1&0&5\\ 0&0&0&1&1 \end{bmatrix}=[I\quad \bold{y}]
y=[−9−451]y= \begin{bmatrix} -9\\-4\\5\\1 \end{bmatrix}
  • Ux=yU\text{x}=y에서 UU와 yy를 알고 있으므로 x를 구할 수 있다.
[Uy]=([U][x1x2x3x4]=[−9−451])=[3−7−22−90−2−12−400−115000−11]∼[10003010040010−60001−1][U\quad \bold{y}] = \begin{pmatrix} \begin{bmatrix} \\&U&\\\\ \end{bmatrix} \begin{bmatrix} x_1\\x_2\\x_3\\x_4 \end{bmatrix} =\begin{bmatrix} -9\\-4\\5\\1 \end{bmatrix} \end{pmatrix} =\begin{bmatrix} 3&-7&-2&2&-9\\ 0&-2&-1&2&-4\\ 0&0&-1&1&5\\ 0&0&0&-1&1 \end{bmatrix} \sim \begin{bmatrix} 1&0&0&0&3\\ 0&1&0&0&4\\ 0&0&1&0&-6\\ 0&0&0&1&-1 \end{bmatrix}
x=[34−6−1]\bold{x}= \begin{bmatrix} 3\\ 4\\ -6\\ -1 \end{bmatrix}

이처럼 L과 U를 알고 있으면 해를 구하기가 쉽다.

🔆 5. LU 구하는 방법 - LU decomposition Algorithm

  • AA가 row replacement만을 사용해서 사다리 꼴(echelon form) 형태로 변환될 수 있다고 가정
  • UU(echelon form)로 변환하기 위한 행 줄임(row operation) 기본 행렬(elementary matrix) E1,  ⋯ ,  EpE_1,\;\cdots,\;E_p가 존재
    • 이 기본 행렬의 역행렬(inverse)이 LL이 됨
  • A가 m × n 행렬일 때 L과 U의 크기는 m × m, m × n이 되어야 함
Ep  ⋯  E1A=UA=(Ep  ⋯  E1)−1U=LUL=(Ep  ⋯  E1)−1E_p\;\cdots\;E_1A=U\\ A=(E_p\;\cdots\;E_1)^{-1}U=LU\\ L=(E_p\;\cdots\;E_1)^{-1}

  • 간단한 예시
[4363]=[10l211][u11u120u22]\begin{bmatrix} 4&3\\ 6&3 \end{bmatrix} =\begin{bmatrix} 1&0\\ l_{21}&1 \end{bmatrix} \begin{bmatrix} u_{11}&u_{12}\\ 0&u_{22} \end{bmatrix}
1⋅u11+0⋅0=41⋅u12+0⋅u22=3l21⋅u11+1⋅0=4l21⋅u12+1⋅u22=3l21=1.5u11=4u11=3u11=−1.5[4363]=[101.51][430−1.5]\begin{aligned} 1\cdot u_{11}+0\cdot0&=4\\ 1\cdot u_{12}+0\cdot u_{22}&=3\\ l_{21}\cdot u_{11}+1\cdot0&=4\\ l_{21}\cdot u_{12}+1\cdot u_{22}&=3\\ \end{aligned}\qquad \begin{aligned} l_{21}&=1.5\\ u_{11}&=4\\ u_{11}&=3\\ u_{11}&=-1.5\\ \end{aligned}\qquad \begin{bmatrix} 4&3\\ 6&3 \end{bmatrix} =\begin{bmatrix} 1&0\\ 1.5&1 \end{bmatrix} \begin{bmatrix} 4&3\\ 0&-1.5 \end{bmatrix}

  • 예시 1 - A가 다음과 같이 주어졌을 때 LU분해

    요약

    1. UU : 각 행의 0이 아닌 첫 열 -\colorbox{#aae0f9}{\color{#aae0f9}-}로 밑 열들(-\colorbox{#d4effb}{\color{#d4effb}-})을 Replacement 하여 0 값으로 만들어 줌
    2. LL : 각 열들의 값의 0이 아닌 첫 행을 Scailing하여 1로 만들어줌
    3. A=LU→Ax=b→LUx=b→Ux=y(치환)→Ly=b→Ux=y→x의해를찾음A=LU \rarr A\text{x}=b \rarr LU\text{x}=b\rarr U\text{x}=y(치환)\rarr Ly=b \rarr U\text{x}=y \rarr x의 해를 찾음
    A=[24−15−2−4−53−812−5−418−607−31]A= \begin{bmatrix} 2&4&-1&5&-2\\ -4&-5&3&-8&1\\ 2&-5&-4&1&8\\ -6&0&7&-3&1 \end{bmatrix}

    • AA가 4개의 행을 갖고 있으므로 LL은 4 × 4가 되어야 함

      A=LU[4×5]=[4×4][4×5]\begin{aligned} A&=LU\\ [4\times 5]&=[4\times 4][4\times 5] \end{aligned}

    • LL을 구하기 위해서 우선 UU(echelon form)를 구해야 함

      [Replacement]1행×2,1행+2행=new2행1행×−1,1행+3행=new3행1행×3,1행+4행=new4행A=[24−15−2-4−53−812−5−418-607−31]∼[24−15−20312−30-9−3−410012412−5]=A1∼A2=[24−15−20312−30002100047]∼[24−15−20312−30002100005]=[2—4−15−20∣3—1—2−3000∣2—10000∣5]=U2행×3,2행+3행=new3행3행×−2,3행+4행=new4행2행×−4,2행+4행=new4행[Replacement][Replacement]\begin{aligned} &\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\scriptsize[\text{Replacement}]\\ &\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\scriptsize1행\times 2,\;\;1행 + 2행 =new 2행 \\ &\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\scriptsize1행\times -1,\;\;1행 + 3행 =new 3행\\ &\quad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\scriptsize1행\times 3,\;\;1행 + 4행 =new 4행 \\ A&= \begin{bmatrix} \colorbox{#aae0f9}2&4&-1&5&-2\\ \colorbox{#d4effb}{-4}&-5&3&-8&1\\ \colorbox{#d4effb}2&-5&-4&1&8\\ \colorbox{#d4effb}{-6}&0&7&-3&1 \end{bmatrix}\sim \begin{bmatrix} 2&4&-1&5&-2\\ \color{tomato}0&\colorbox{#aae0f9}{\color{tomato}3}&\color{tomato}1&\color{tomato}2&\color{tomato}-3\\ \color{tomato}0&\colorbox{#d4effb}{\color{tomato}-9}&\color{tomato}-3&\color{tomato}-4&\color{tomato}10\\ \color{tomato}0&\colorbox{#d4effb}{\color{tomato}12}&\color{tomato}4&\color{tomato}12&\color{tomato}-5 \end{bmatrix}=A_1\\\\ \sim A_2&=\begin{bmatrix} 2&4&-1&5&-2\\ 0&3&1&2&-3\\ \color{tomato}0&\color{tomato}0&\color{tomato}0&\colorbox{#aae0f9}{\color{tomato}2}&\color{tomato}1\\ \color{tomato}0&\color{tomato}0&\color{tomato}0&\colorbox{#d4effb}{\color{tomato}4}&\color{tomato}7 \end{bmatrix}\sim \begin{bmatrix} 2&4&-1&5&-2\\ 0&3&1&2&-3\\ 0&0&0&2&1\\ \color{tomato}0&\color{tomato}0&\color{tomato}0&\color{tomato}0&\colorbox{#aae0f9}{\color{tomato}5} \end{bmatrix}= \begin{bmatrix} \underset{\text{---}}{\color{blue}2}&\color{blue}4&\color{blue}-1&\color{blue}5&\color{blue}-2\\ 0|&\underset{\text{---}}{\color{blue}3}&\underset{\text{---}}{\color{blue}1}&\color{blue}2&\color{blue}-3\\ 0&0&0|&\underset{\text{---}}{\color{blue}2}&\color{blue}1\\ 0&0&0&0|&\color{blue}5 \end{bmatrix}=U \\ &\qquad\scriptsize2행\times 3,\;\;2행 + 3행 =new 3행 \qquad \scriptsize3행\times -2,\;\;3행 + 4행 =new 4행 \\ &\qquad\scriptsize2행\times -4,\;\;2행 + 4행 =new 4행 \;\quad\scriptsize[\text{Replacement}] \\ &\qquad\scriptsize[\text{Replacement}] \end{aligned}

    • LL은 AA의 각각 pivot column에서 pivot 아래의 entry를 pivot으로 나눠주면 구할 수 있다.

      [2-42-6][3-912][24][5]÷2  ÷3  ÷2÷5    ↓  ↓  ↓  ↓[1−211−31−3421],andL=[1000−21001−310−3421]\begin{aligned} \begin{bmatrix} \colorbox{#aae0f9}2\\ \colorbox{#d4effb}{-4}\\ \colorbox{#d4effb}2\\ \colorbox{#d4effb}{-6} \end{bmatrix} \begin{bmatrix} \\ \colorbox{#aae0f9}3\\ \colorbox{#d4effb}{-9}\\ \colorbox{#d4effb}{12} \end{bmatrix} \begin{bmatrix}\\\\ \colorbox{#aae0f9}2\\ \colorbox{#d4effb}{4}\\ \end{bmatrix} \begin{bmatrix}\\\\\\ \colorbox{#aae0f9}5\\ \end{bmatrix}\\ \color{#5bb3ef} \div2\quad\;\div3\quad\;\div2\quad\div5\;\;\\ \color{#5bb3ef}\darr\qquad\;\darr\qquad\;\darr\qquad\;\darr\quad \\ \begin{bmatrix} 1\\ -2&&1\\ 1&&-3&&1\\ -3&&4&&2&&1 \end{bmatrix},&\quad\text{and}\quad&L=\begin{bmatrix} 1&0&0&0\\ -2&1&0&0\\ 1&-3&1&0\\ -3&4&2&1 \end{bmatrix} \end{aligned}

  • 예시2

    Find an LU factorization of A=[2−4−236−9−582−7−394−2−2−1−6334]\text{Find an LU factorization of }A= \begin{bmatrix} 2&-4&-2&3\\ 6&-9&-5&8\\ 2&-7&-3&9\\ 4&-2&-2&-1\\ -6&3&3&4 \end{bmatrix}

    • 행 줄임(row reduction) 연산으로 U 구하기

      A=[2−4−236−9−582−7−394−2−2−1-6334]∼[2−4−23031−10-3−16062−70-9−313]∼[2−4−23031−10005000-500010]∼[2−4−23031−1000500000000]=U\begin{aligned} A&= \begin{bmatrix} \colorbox{#aae0f9}2&-4&-2&3\\ \colorbox{#d4effb}6&-9&-5&8\\ \colorbox{#d4effb}2&-7&-3&9\\ \colorbox{#d4effb}{4}&-2&-2&-1\\ \colorbox{#d4effb}{-6}&3&3&4 \end{bmatrix}\sim \begin{bmatrix} 2&-4&-2&3\\ 0&\colorbox{#aae0f9}3&1&-1\\ 0&\colorbox{#d4effb}{-3}&-1&6\\ 0&\colorbox{#d4effb}6&2&-7\\ 0&\colorbox{#d4effb}{-9}&-3&13 \end{bmatrix}\\\\ \sim &\begin{bmatrix} 2&-4&-2&3\\ 0&3&1&-1\\ 0&0&0&\colorbox{#aae0f9}5\\ 0&0&0&\colorbox{#d4effb}{-5}\\ 0&0&0&\colorbox{#d4effb}{10} \end{bmatrix}\sim \begin{bmatrix} 2&-4&-2&3\\ 0&3&1&-1\\ 0&0&0&5\\ 0&0&0&0\\ 0&0&0&0 \end{bmatrix}=U \end{aligned}

    • UU를 구하는 과정에서 구한 AA의 pivot column을 이용해서 LL을 구함

      [2624-6][3-36-9][5-510]    ÷2  ÷3  ÷5  ↓  ↓  ↓      [1311−11⋯22−1−3−32],andL=[10000310001−110022−110−3−3201]\begin{aligned} \begin{bmatrix} \colorbox{#aae0f9}2\\ \colorbox{#d4effb}{6}\\ \colorbox{#d4effb}2\\ \colorbox{#d4effb}4\\ \colorbox{#d4effb}{-6} \end{bmatrix} \begin{bmatrix} \\ \colorbox{#aae0f9}3\\ \colorbox{#d4effb}{-3}\\ \colorbox{#d4effb}6\\ \colorbox{#d4effb}{-9}\\ \end{bmatrix} \begin{bmatrix}\\\\ \colorbox{#aae0f9}5\\ \colorbox{#d4effb}{-5}\\ \colorbox{#d4effb}{10}\\ \end{bmatrix}\quad\;\; \\ \color{#5bb3ef} \div2\quad\;\div3\quad\;\div5\qquad\;\\ \color{#5bb3ef}\darr\qquad\;\darr\qquad\;\darr\qquad\;\;\; \\ \begin{bmatrix} 1\\ 3&1\\ 1&-1&1&\cdots\\ 2&2&-1\\ -3&-3&2 \end{bmatrix},&\quad\text{and}\quad&L=\begin{bmatrix} 1&0&0&0&0\\ 3&1&0&0&0\\ 1&-1&1&0&0\\ 2&2&-1&1&0\\ -3&-3&2&0&1 \end{bmatrix} \end{aligned}

🔆 6. 수와 관련된 메모 - Numerical Notes

  • A−1A^{-1}로 해를 구했을 때 보다 LU 분해의 연산량이 1/3배 적음
  • 또한 A가 sparse(대부분이 0으로 채워져있는 경우)하면 L과 U도 sparse 함
  • 하지만 A−1A^{-1}는 dense(값이 많은 경우) 함
  • 이 의미는 L과 U를 저장하는 memory와 A−1A^{-1} 값을 저장하는 memory의 차이가 큰 것을 의미
  • 공학적인 문제를 풀 때 LU 분해는 속도와 메모리적 측면에서 큰 이점을 얻을 수 있음
profile
yeppi1802
제로베이스 DA7 김예빈입니다.
이전 포스트

선형대수 : 03 선형대수학 - 4 : 역행렬, 역행렬 특징

다음 포스트

선형대수 : 03 선형대수학 - 6 : 행렬식

0개의 댓글