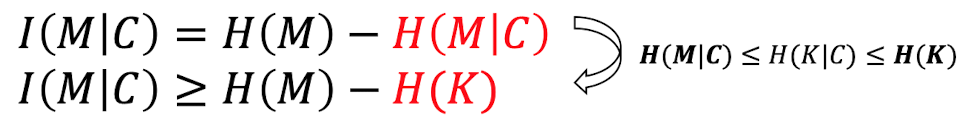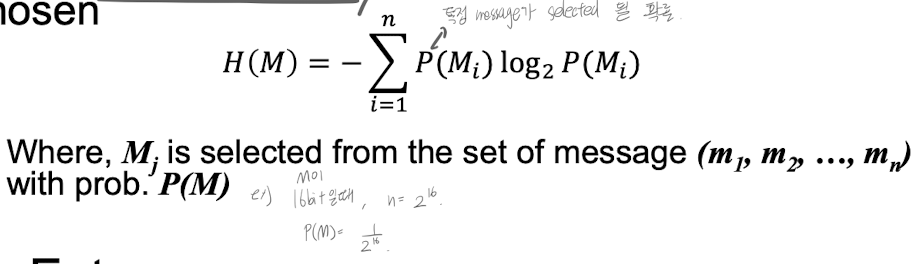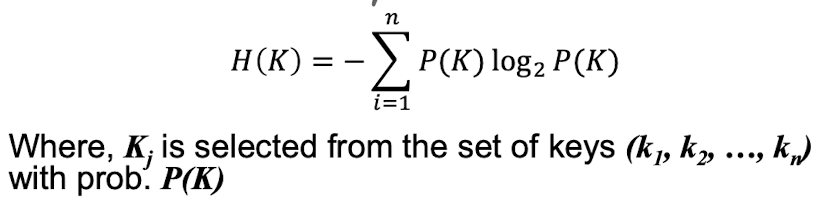💬 Overview

• get-in : btd paradox, digital signature susceptibility
• model of secure system
  - condition for perfect secrecy
  • shannon entroyphy
  • equivocation(모호성)
  • perfect secrecy (Priori & Posterior Probability)
  • redundancy
  • unicity distance
• complexity theroy

🪜 Get in

Birthday paradox

about 50% change of having a same birthday when there are 23 people!

P(n) = prob that at least two have a same BTD when there are n persons

P(n) = 1 - P'(n)
(P'(n) = no one has same BTD)

P(1) = 1
P(2) = 1 * (365-1)/365
P(3) = 1 * (365-1)/365 * (365-2)/365

Digital Seignature Susceptibility

susceptibility : 민감성

---

🍦 Model of contents

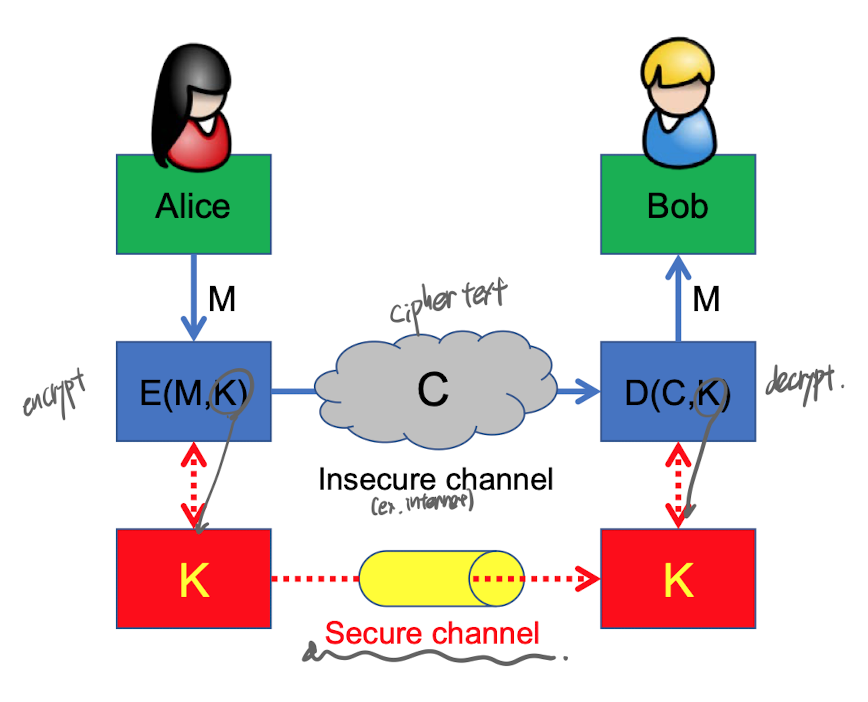
✨Shannon theory

communication theory of secrecy system

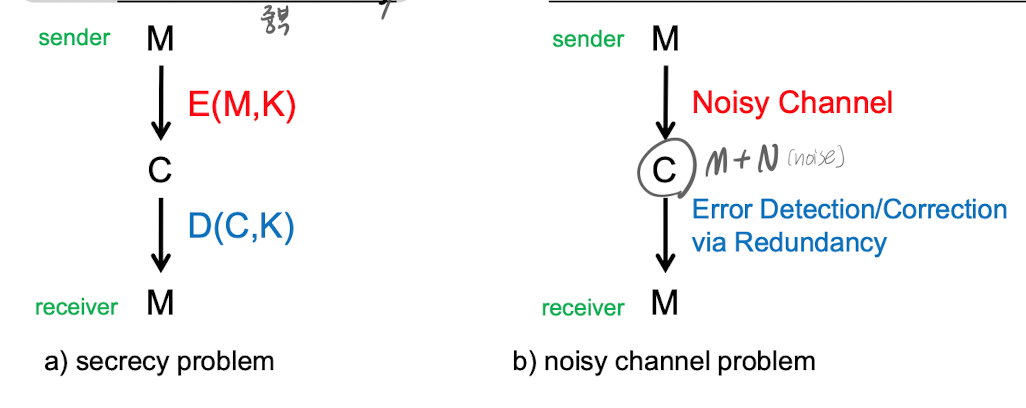
similar to "noisy channel problem"
i.e) A user wishing to send a message over a noisy channel must add redundancy to allow detection/correction of errors.

• noisy channel : M을 전송하는데, 노이즈에 의해 C로 변화된 M을 에러탐색과 수정을 통해 다시 M으로 수정

✨PERFECT SECRECY - Priori & Posterior Probability

✔️ in words..

암호화되기전 (pri) Key의 확률, Message의 확률과
암호화 된 후 (post) 공격자가 cipher text를 통해 가능한 key와 message를 계산하는 가능성

• Pi : key의 확률 : A Kj is selected from the set of all keys K with probability Pi
• Mj : Message 의 확률 : A msg Mj is selected from the set of all msgs M with a priori probability Qj
  (i.e. data가 16bit면 2^16가지의 msg 경우가 있다.)
• C = E(Mj, Ki)
  => C를 관찰한 Attacker 는 가능한 Mj와 Ki의 postterior probability를 계산할 수 있다.
  => posteriori probability = attacker's knowledge를 represent

✔️ in calc..

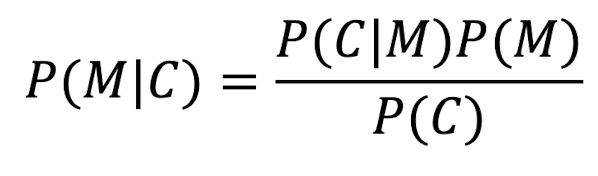
• P(M|C) = C를 얻은 attacker가 제대로 M을 해독할 확률 = prob. of M given C intercepted
• P(C|M) = M에 의해 C가 생성될 확률 = prob. of C generated by M
• P(M) = M이 선택될 확률 = prob. of M being selected
• P(C) = C가 입수될 확률 = prob. of obtaing C

✔️ Condition for PERFECT SECRECY

🤔 IF P(M|C) = P(M) for all C & M
attacker gain NO info by intercepting C

= c가 강탈되었을때조차 M을 (랜덤) 선택하는 확률과 같다.
= c를 강탈해도 M에 대한 정보를 얻는 것이 없다

🤭 So Perfect Securecy is
1. P(M|C) = P(M) for all C & all M
2. P(C|M) = P(C) for all C & all M

🤭 So Perfect System is
= as many C's as M's
= at least one K transforming any M into these C's.

this works for guessing imppossible XXD

these are neccessary and sufficient condition !

✨ Shannon Entropy

✔️ definition

measure of unpredictability in random variable
(높을 수록 예측하기 힘들다!)

✔️ Examples

1) Political Poll

• Entrophy(H) is large : round 1 - outcome of poll is not already known 'unpredictable'
  i.e.) Outcome of the poll and learning the result / gives / some new info!
• Entrophy(H) is small : round 2 - same poll performed after the first round
  i.e) outcome of the first-round poll / already known / and the second poll can be predicted.
  

2) Coin Flipping (fair coin case)

• Entropy(H) = 1 = 전혀 예측 불가능
• P(head) = P(tail) = no way to predict!

✔️ Calc..

Message Entrophy
= amount of info produced / when a message is chosen

Key Entropy
= amount of info produced / when a key is chosen

✔️ Observation

• the amount of uncertainty introduced into the system / cannot be greater than the key uncertainty.

• K uncertanity is at least M uncertainty
  (K엔트로피 >= M엔트로피) = M info is perfectly concealed
  
  occurs when all M's are equally probable (i.e. totally random)

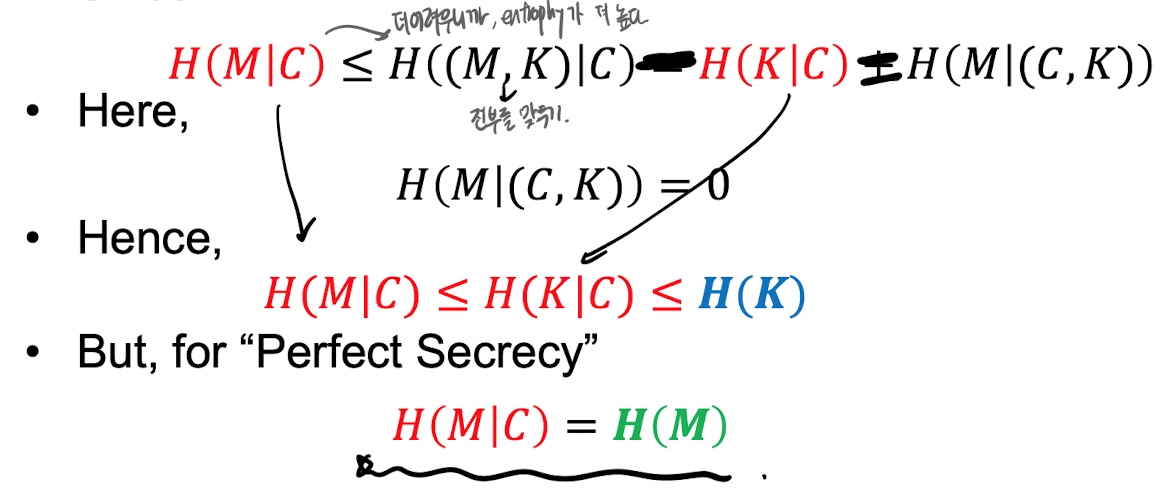
✨ equivocation(모호성)

✔️ Definition

Conditional entropies of K and M
(i.e., unpredictability of the K and M given an intercepted C.)

✔️ Properties

N = intercepted된 C 일부분 길이
H(K, N|C) is a non-increasing function of N

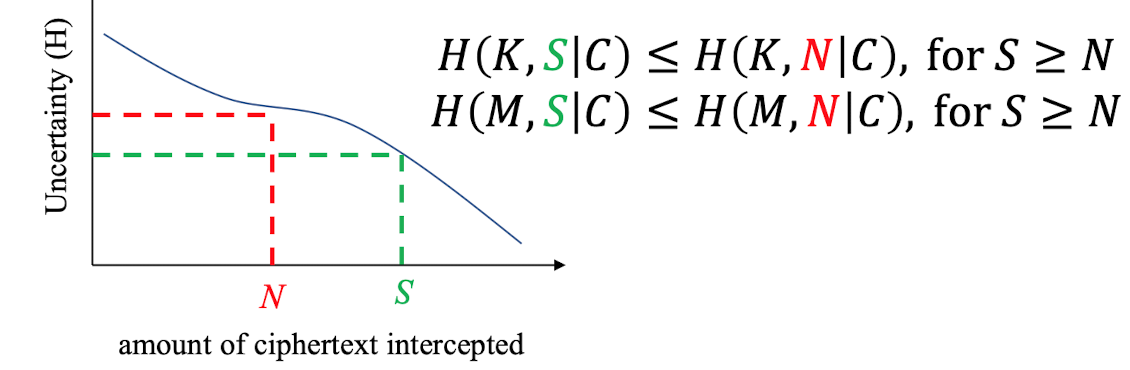
i.e., it's theoretically easier to determine the key as more C is intercepted. C가 많이 intercept될수록 K를 determine 하기 쉬워짐

✔️ For perfect secrecy!

Mutual Info
- I(M|C) = C가 주어졌을때 M에 대해 얻을수있는 정보의 양
- I(K|C) = C가 주어졌을때 K에 대해 얻을 수 있는 정보의 양

I(M|C) = H(M) - H(M|C)

"new info revealed knowing C"
= "uncertainty" - "uncertainty after knowing C"

How to achieve perfect secrecy?

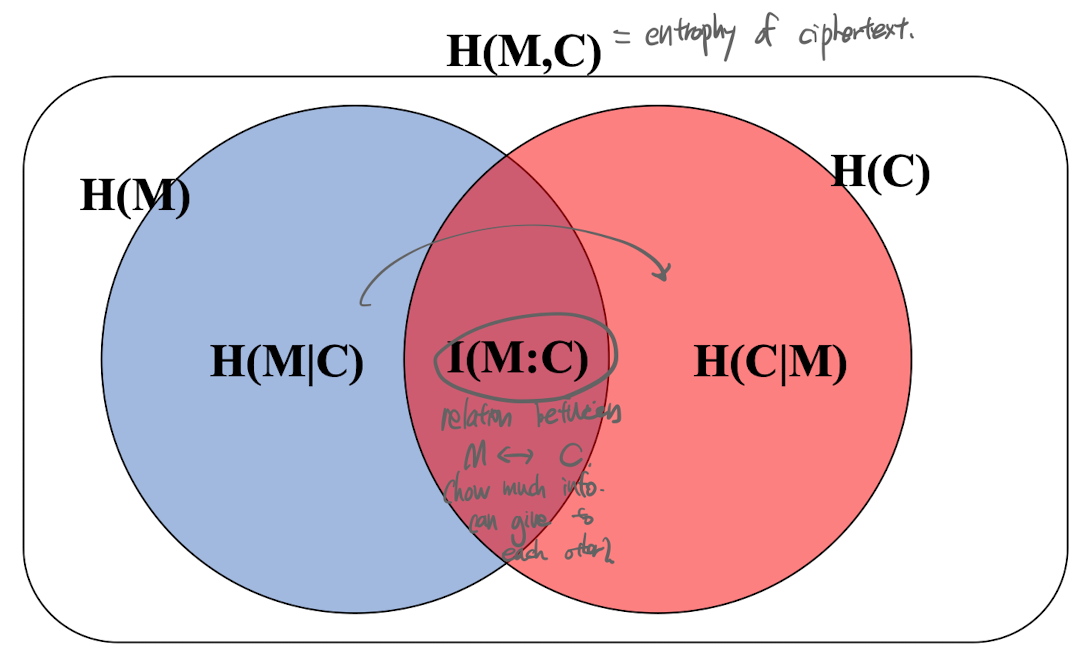
I(M|C) = H(M) - H(M|C) = 0
H(M) = H(M|C)

= C and M are statistically independent

also

H(M) <= H(K)
= 적어도 K엔트로피는 M엔트로피보다 커야!
= num of M bits <= num of K bits
since..

otherwise,,
like H(M) > H(K) !
Cryptanalyst can obtain a lot of info about plaintext.