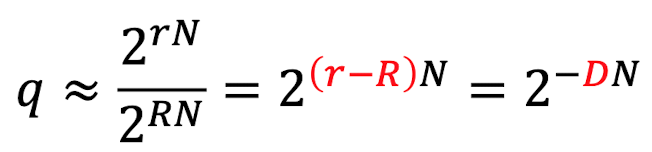💬 Overview

• get-in : btd paradox, digital signature susceptibility
• model of secure system
  - condition for perfect secrecy
  • shannon entroyphy
  • equivocation(모호성)
  • perfect secrecy (Priori & Posterior Probability)
  • redundancy
  • unicity distance
• complexity theroy

✨ Redundancy 중복

✔️ defintion

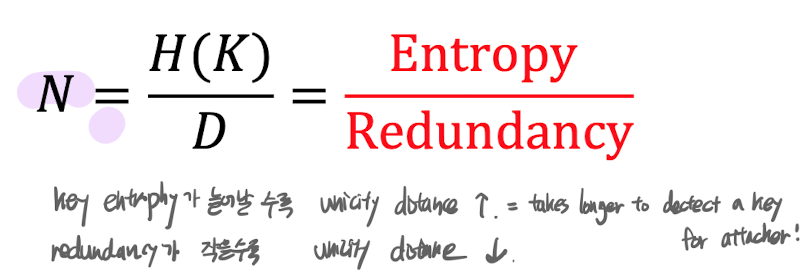
D = redundancy of language = R - r

R = absolute rate of language
r = rate of the language

ex) So redundancy of english is
D = R - r = 4.7 - 1.5 = 3.2 (bits/letter)

ex) R random : QWJK SB A EIWPCMH
r random : THIS IS A EXAMPLE

✔️ consider a decipherment

• M' = D(C, K)
• M' = independent random variable uniformly distributed over all 2^RN M of length N (both meaningful and meaning less)

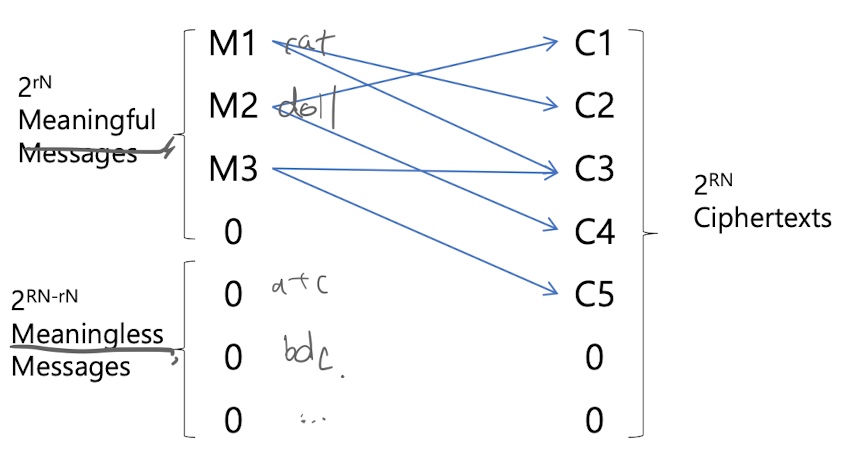
2^rN개의 meaningful M들은 2^RN개의 C에 고르게 분포된다.

✔️ Spurious Key

그럴싸한 가짜 키

C = E(M,K) = E(M', K')
= 공격자가 그럴싸한 다른 키를 고른 상황

• Given : C = E(M,K)
• Gives : another K' generating the same C

• 모든 올바른 C에 대해서, (2^H(K) - 1) = attacker가 틀린 답을 try하는 갯수 일때, 각각 틀린답을 산출하는 확률 q를 가짐

만약 각각의 Plain text(2^rN개) 가 고른 분포를 가지고 있고,
Cipher text(2^RN개) 에서 틀린 답이 산출될 확률 은

✨ Unicity Distance

✔️ definition

= 복잡성이 0이 되는 C의 특정길이
= C를 intercpet하는 횟수가늘어날수록 key 의 entrophy가 줄어든다

• original C의 길이는 필요하다
  to break C by reducing the num of spurious K to zero

✔️ calc..

F를 0으로 둔다 = false solution 이 충분히 작아진다
0 = H(K) - DN

그러므로 unicity distance(N)은

✔️ examples

DES's unicity distance

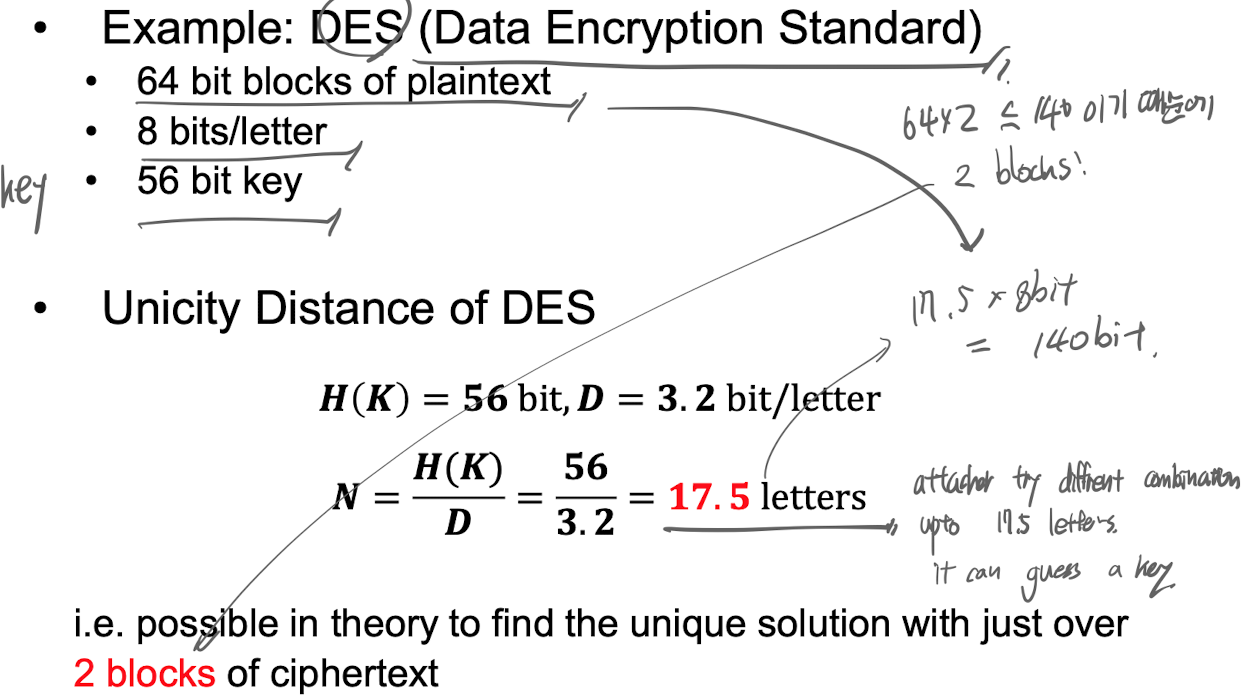
대략 2블록 이상의 C가 있으면 해결책 찾을 수 있음

✨ Computational Complexity Theory

✔️ algorithm complexity

• 시간 T

• 공간 S

• 입력크기 n

• F(n) = an^t + bn^(t-1) .... + z =O(n^t)
  (가장 큰 차수를 대표로 O안에 넣는다)

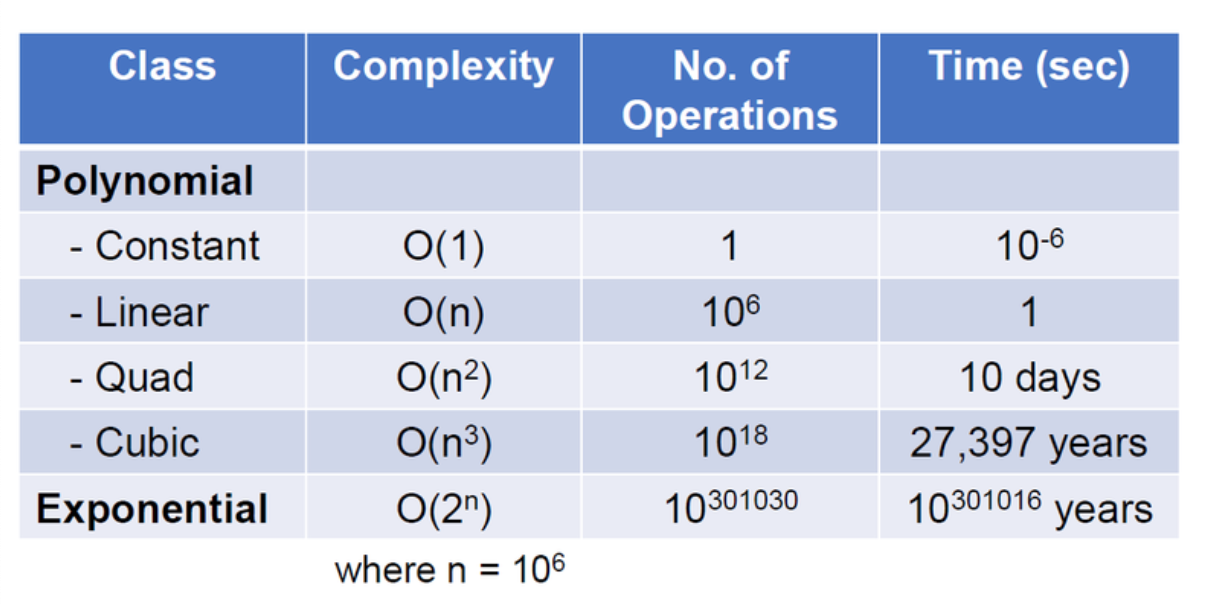
✔️ time, space complexity

time, space 모두 problem을 해결하는데 고려된다.

✔️ turing machine

• consider a finite-state theoretical machine (running a program/algorithm)
  - by inifinite memory
  • to examine the abilities and limit of computer

• Deterministic turing machine
  - at most one action for any given situation
  • 어떤 상황에서도 최대 한개의 동작
• Non-Deterministic turing mahcine
  - more than one possible action for given situation
  • i.e., NTM은 polynomial time안에 solution들을 try 하도록 allowed
    n개의 처리가능한 문제들과 n개의 머신이 있으면 동시에 모두 check 가능

✔️ Polynomial Time Problem(P)

polynomial = 다항의

• polynomial time에 해결가능 = cryptographyically strong 하지 않다

✔️ Non-Deterministic polynomial (NP)

• 비결정성 다항식
• solvable in polynomial time on a non-deterministic machine
• 만약 attacker들이 solution을 guess하면 polynomial time안에 cheked 될 수 있다.

• systematic solution to NP problem은 exponential time(지수/기하급수적) 걸림
• ex) knapsack progle, discrete logarithm problem, integer factorization problem

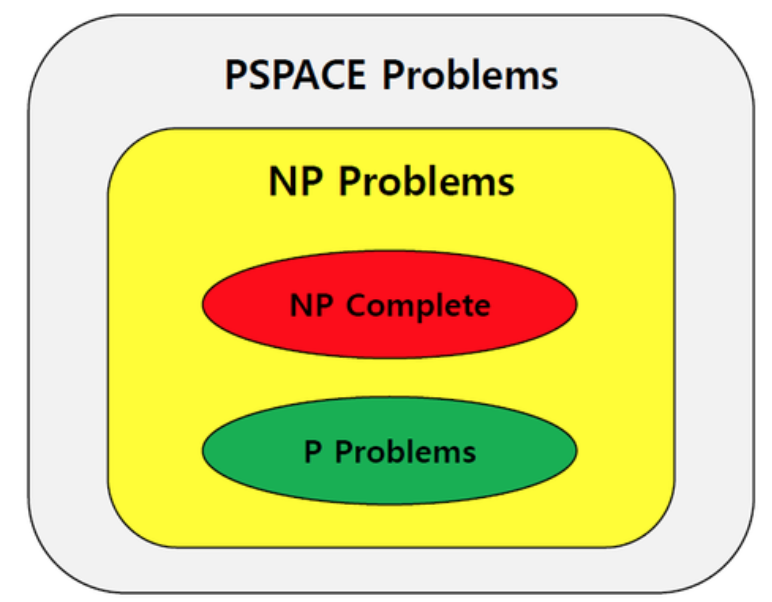
✔️ PSPACE

some problems can be solved

• with polynomial space
• but not with polynomial time

=> harder than NP problems.

✔️ range of problems