[금융] Efficient Frontier/CML 효율적 투자선과 자본시장선

📁 Modern Portfolio Theory 포트폴리오 이론

💸 Portfolio의 기대수익률과 위험

기대수익률: 수익률의 평균

위험: 수익률의 분산 또는 표준편차

• $\sigma = 0$ : 무위험자산 (예금, 국공채 등)
• $\sigma \neq 0$ : 위험자산 (대부분의 자산)
  $\sigma_p^2 = \sum_{i}{w_i\{R_i-E(R_p)\}^2} = \text{w}^TP\text{w}$
  $(\text{w}:\ 가중치\ 벡터,\ \text{P}:\ 공분산\ 행렬)$

💡 Efficient Frontier 효율적 투자선

📚 포트폴리오 집합

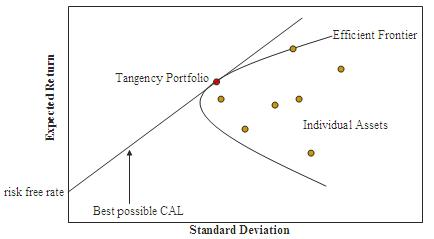
• MPT로 도출된 각 포트폴리오의 기대수익률과 위험 수준을 바탕으로, 가능한 모든 포트폴리오들을 위험-기대수익률 그래프에 표시해 보았다.

  MPT의 지배원리: 효율적인 포트폴리오

  • 동일 위험 수준: 기대수익률이 높은 포트폴리오
  • 동일 기대수익률: 위험 수준이 낮은 포트폴리오

• 지배원리에 따라 효율적인 포트폴리오들을 선택하면, 최소 분산 포트폴리오를 시작으로 concave한 곡선이 그려진다.
• 그 선이 효율적 투자선(Efficient Frontier)이다.

🏗️ 무위험자산을 고려한 포트폴리오 재구성

💵 자본배분선(CAL : Capital Allocation Line)

• $\sigma=0$ 선상의 한 무위험자산($R_f$)을 고려하여 포트폴리오를 재구성해보자.
• 효율적 투자선상의 포트폴리오들과 무위험자산을 직선으로 연결해, 여러 기울기의 자본배분선(CAL)을 그릴 수 있다.
• 지배원리에 의해, 가장 효율적인 CAL은 효율적 투자선에 tangency한 CAL라고 할 수 있다.

💰 시장 포트폴리오(Market Portfolio)

• 해당 접점에 위치한 포트폴리오를 시장 포트폴리오라고 한다.

무위험자산이 존재할 때, Efficient Frontier 상에 존재하는 위험자산 포트폴리오 중 가장 효율적인 포트폴리오

시장 포트폴리오의 특징

• 가능한 모든 투자가능자산들로 구성됨
• 각 자산의 시가총액 비율대로 평균/분산이 가중되어 있음

시장 포트폴리오의 기대수익률($E(R_m)$)과 위험($\sigma_m$)

• 시가총액법으로 산출한 종합주가지수를 이용하여 계산 가능

📈 자본시장선(CML, Capital Market Line)

• 해당 tangent line을 자본시장선(CML)이라고 한다.

무위험자산과 시장 포트폴리오로 구성된 효율적인 포트폴리오들의 집합