[금융] SML/CAPM 증권시장선과 자본자산 가격결정 모형

🏃‍♀️ CAPM을 학습하기 전에

📈 자본시장선 CML: Capital Market Line이란?

• 포트폴리오의 총 위험과 기대수익률의 관계식

📈 증권시장선 SML: Security Market Line이란?

• 포트폴리오의 체계적 위험과 기대수익률의 관계식

📉 분산투자효과 Diversification Effect

• 포트폴리오를 구성하는 투자자산의 수가 증가하면 포트폴리오의 위험 수준이 낮아진다.
• 포트폴리오의 위험은 구성 투자자산의 위험을 투자금 비율로 가중평균한 값보다 작다.
  • 투자자산 간의 상관계수($\rho$) 때문

⚠️ 체계적 위험 Systematic Risk

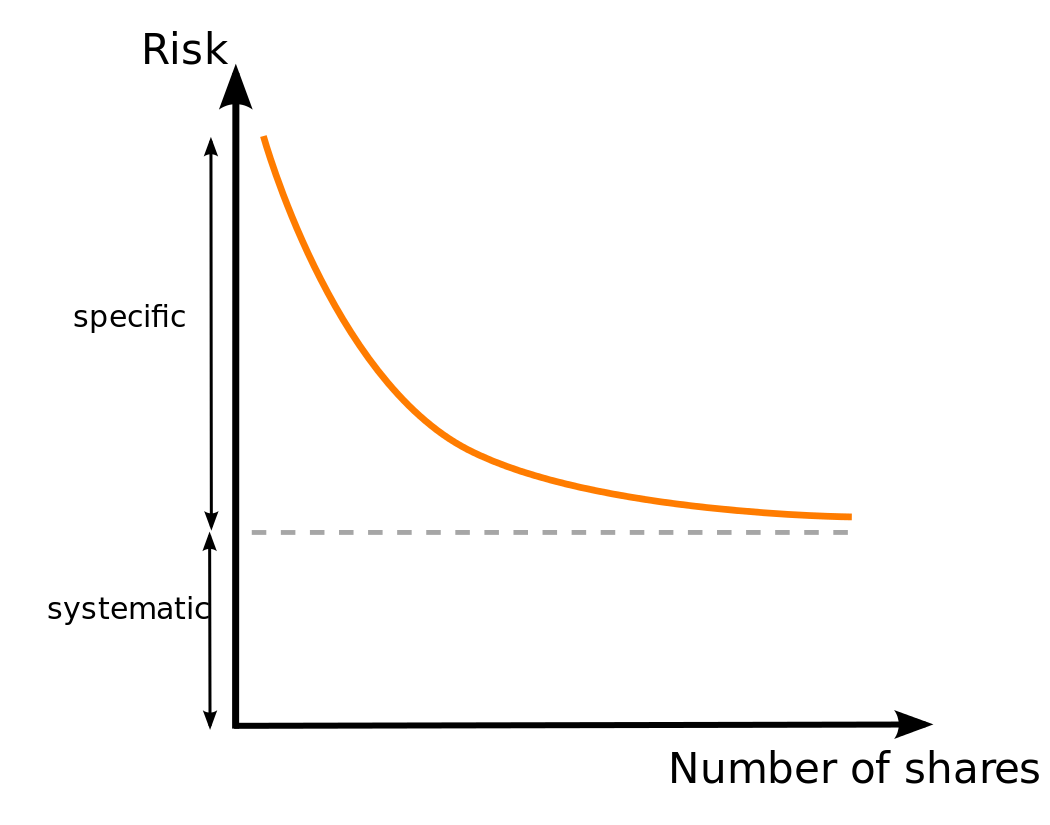
• 포트폴리오를 구성하는 투자자산의 수를 무한으로 늘려도 위험은 0에 수렴하지 않는다.
• 분산투자효과와 무관하게 어느 투자 상황에서나 공통적으로 존재하는 위험을 체계적 위험이라고 한다.

비체계적 위험

• 분산투자로 제거 가능한 위험
• 개별 기업의 고유 요인(신제품 출시, 오너 리스크, 노사 분쟁 등)으로 발생 $\rightarrow$ 고유위험

체계적 위험

• 분산투자로 제거 불가능한 위험
• 시장 요인(경제 성장, 금리 인상, 환율 하락 등)으로 발생 $\rightarrow$ 시장위험

📐 체계적 위험의 측정

👫 공분산 : 개별 투자자산과 시장 포트폴리오의 관련성

• 체계적 위험의 절대적 크기

β 베타 계수 Beta Coefficient

• 시장 포트폴리오의 변동성에 대한 개별자산 또는 포트폴리오의 상대적인 변동성 비율
  $\beta_i = \frac{Cov(R_i, R_m)}{Var(R_m)} = \frac{\sigma_{i,m}}{\sigma_m^2}$

$\beta_i$ : $R_m$을 종속변수로 하는 $R_i$ 회귀 직선의 기울기

β 베타 계수의 특징과 예시

$\vert\beta_i\vert>1$ : 공격적 투자
$\vert\beta_i\vert<1$ : 방어적 투자

※ 시장 포트폴리오의 베타 계수

📈 증권시장선 SML

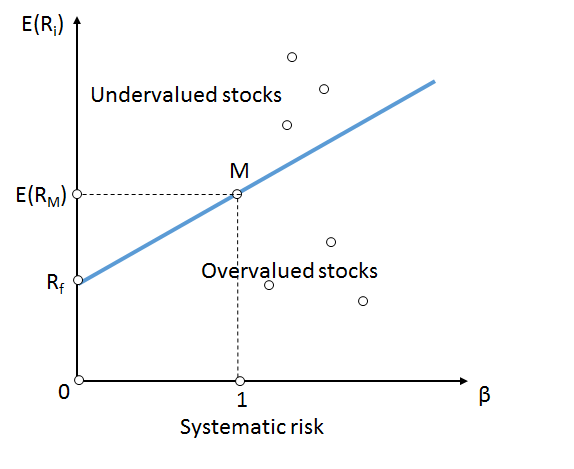
• 체계적 위험($\beta_i$)과 기대수익률($E(R_i)$)의 선형 관계식

🌟 증권시장선의 의미

SML 위에 위치한 자산: 저평가 자산
SML 아래에 위치한 자산: 고평가 자산

🎉 자본자산 가격결정 모형(Capital Asset Pricing Model, CAPM)

자본시장의 지배원리 하에 자산의 균형수익률을 찾는 모형

📈 자본시장선 CML

• 무위험자산과 시장 포트폴리오로 구성된 포트폴리오의 균형수익률
  $E(R_p) = R_f + (\frac{E(R_m) - R_f}{\sigma_m})\sigma_p$

β 베타 계수

• 시장 포트폴리오의 수익률 변화에 따른 개별자산/포트폴리오의 수익률 변화
  $\beta_i = \frac{Cov(R_i, R_m)}{Var(R_m)} = \frac{\sigma_{i,m}}{\sigma_m^2}$

📈 증권시장선 SML

• 개별자산/포트폴리오의 균형수익률
  $E(R_i) = R_f + (E(R_m) - R_f)\beta_i$

📚 References

Beta Coefficient | CFI™️
Systematic risk | Wikipedia
Capital asset pricing model | Wikipedia