Weight Initialization(가중치 초기화)

• 가중치가 너무 작게 초기화되면 그래디언트 소실 문제가 발생할 수 있으며, 반대로 가중치가 너무 크게 초기화되면 그래디언트 폭주 문제가 발생할 수 있다

Zero initialization

• 신경망의 가중치를 모두 0으로 초기화하는 방법
• 간단하고 계산이 빠르다는 장점이 있지만, 실제로는 잘 사용되지 않는다
• 대칭성 문제
  • 모든 가중치가 0으로 초기화되면, 모든 뉴런이 동일한 출력을 생성한다
  • 이는 역전파 과정에서 모든 뉴런이 동일한 그래디언트를 받게 되므로, 가중치 업데이트가 동일하게 이루어진다
  • 이를 '대칭성 문제(Symmetry Problem)'라고 하며, 이로 인해 모델이 복잡한 패턴을 학습하는 데 어려움을 겪게된다
• Gradient Vanishing 문제
  • 특정 활성화 함수(예: 시그모이드 함수, 하이퍼볼릭 탄젠트 함수)를 사용할 경우, 초기 가중치가 0이면 그래디언트가 소실되는 문제가 발생할 수 있다

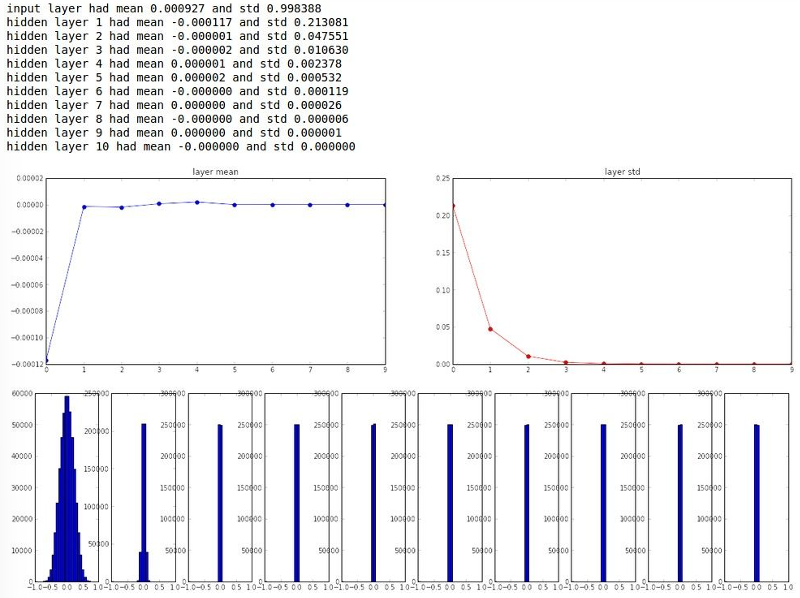
임의의 작은 값으로 초기화

• 작은 네트워크에서는 충분하지만 깊은 네트워크에서는 문제가 발생한다
• Zero 초기화와 마찬가지로 Gradient Vanishing 문제가 발생한다

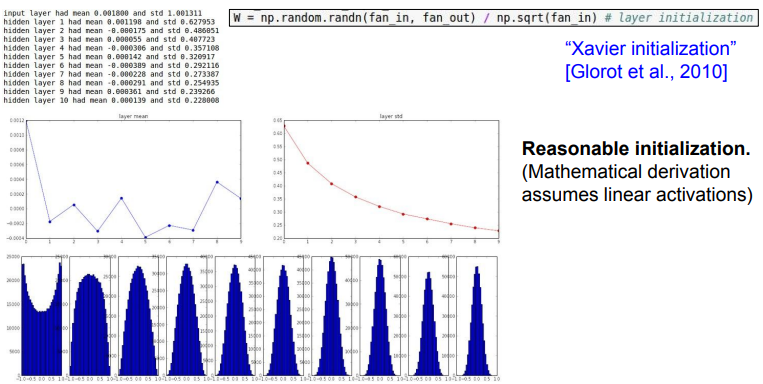
Xavier initialization

• 신경망의 각 레이어에서 출력값의 분산이 입력값의 분산과 동일하게 유지되도록 가중치를 초기화하여, 심층 신경망의 학습을 안정화하고 속도를 높이는 데 도움을 준다
• Xavier 초기화는 가중치를 균일 분포 또는 정규 분포로 초기화하되, 분포의 범위가 특정한 방식으로 결정된다. 특히, 가중치의 초기 분포 범위는 해당 레이어의 입력 노드 수와 출력 노드 수에 의해 결정된다
• Xavier 초기화는 활성화 함수가 선형이거나 그 중심 부분이 선형인 경우에 잘 작동된다
  • 예를 들어, Sigmoid 함수나 Hyperbolic Tangent 함수와 같은 S-형 함수에 대해서는 Xavier 초기화가 효과적이다
  • 그러나 ReLU 함수와 같이 비선형성이 강한 함수에 대해서는 He 초기화 등 다른 방법이 더 적합할 수 있다

W = np.random.randn(fan_ubm fan_out) / np.sqrt(fan_in)

• Standard gaussian으로 뽑은 값을 "입력의 수"로 스케일링해준다
• 입/출력의 분산을 맞춰준다
• 입력의 수가 작으면 더 작은 값으로 나누고 좀 더 큰 값을 얻는다
• 우리는 더 큰 가중치가 필요하다. 왜냐하면 작은 입력의 수가 가중치와 곱해지기 때문에, 가중치가 더 커야만 출력의 분산 만큼 큰 값을 얻을 수 있기 때문이다
• 반대로 입력의 수가 많은 경우에는 더 작은 가중치가 필요하다
• 각 레이어의 입력이 Unit gaussian이길 원한다면 이런 종류의 초기화 기법을 사용해볼 수 있다
• 각 레이어의 입력을 Unit gaussian스럽게(approximately) 만들어 줄 수 있다
• 여기서 가정하는 것은 현재 Linear activation이 있다고 가정하는 것이다

문제점

• ReLU를 쓰면 잘 동작하지 않는다
  • ReLU는 출력의 절반을 죽이는데 그 절반은 매번 0이 된다. 그래서 결국 출력의 분산을 반토막 내버린다.
  • 그러므로 이전과 같은 가정을 해버리면 ReLU에서는 잘 작동하지 않는다. 값이 너무 작아지는 것이다

해결법

W = np.random.randn(fan_ubm fan_out) / np.sqrt(fan_in/2)

• 추가적으로 2를 더 나눠준다
• 뉴런들 중 절반이 없어진다는 사실을 고려하기 위해서이다
• 일제 입력은 반밖에 안들어가므로 반으로 나눠주는 텀을 추가적으로 더해 주는 것이고 실제로 잘 동작한다

Batch Normalization

• 딥러닝 모델의 학습 속도를 높이고, 그래디언트 소실 문제를 완화하는 등의 효과를 주는 방법이다
• 각 레이어의 입력 분포를 정규화함으로써 레이어의 학습을 독립적으로 만들어 준다
• 이는 각 레이어가 이전 레이어의 변화에 영향을 받지 않고, 자신의 학습에만 집중할 수 있게 해준다
• Batch 단위로 한 레이어에 입력으로 들어오는 모든 값들을 이용해서 평균과 분산을 구해서 Normalization 해준다
• 평균과 분산을 "상수"로 가지고만 있으면 언제든지 미분이 가능하며 따라서 Backprop이 가능하게 된다
• Batch Normalization 연산은 FC나 Cov Layer 직후에 넣어준다
• 깊은 네트워크에서 각 레이어의 W가 지속적으로 곱해져서 Bad scaling effect가 발생했지만 Normalization은 그 bad effect를 상쇄시켜 버린다
• 입력의 스케일만 살짝 조정해 주는 역할이기 때문에 FC와 Conv 어디에든 적용할 수 있다
• Conv Layer에서 차이점이 있다면 Normalization을 차원마다 독립적으로 수행하는 것이 아니라 같은 Activation Map의 같은 채널에 있는 요소들은 같이 Normalize 해준다. 왜냐하면 Conv 특성상 (convolutional property) 같은 방식으로 normalize 시켜야 하기 때문이다
• Conv Layer의 경우 Activation map(채널, Depth) 마다 평균과 분산을 하나만 구한다. 그리고 현재 Batch에 있는 모든 데이터로 Normalize 해준다
• 요약하자면 입력을 가지고 mini-batch에서의 평균을 계산한다. 모든 mini-batch 마다 각각 계산해준다. 분산도 계산해준다
• 평균과 분산으로 Normalize 한 이후에 다시 추가적인 scaling, shifting factor를 사용한다
• BN은 gradient의 흐름을 보다 원활하게 해주며 결국 더 학습이 더 잘되게(robust) 해준다
• BN을 쓰면 learning rates를 더 키울 수도 있고 다양한 초기화 기법들도 사용해 볼 수 있다
• BN이 regularization의 역할도 한다는 것도 중요하다
• 각 레이어의 출력은 해당 데이터 하나 뿐만 아니라 batch 안에 존재하는 모든 데이터들에 영향을 받는다(평균, 분산). 왜냐하면 각 레이어의 입력은 해당 배치의 (표본)평균으로 Normalize 되기 때문이다
• 그렇기 때문에 이 레이어의 출력은 이제 오직 하나의 샘플에 대한 deterministic한 값이 아니게 되고 Batch 내의 모든 데이터가 입력으로 한대 묶인다고 볼 수 있다
• 그러므로 더 이상 레이어의 출력은 deterministic하지 않고 조금씩 바뀌게 되고 이는 regularization effect를 준다

특징

• 학습 속도 개선
  • 각 레이어의 입력 분포를 정규화함으로써 그래디언트의 흐름을 개선하고, 학습 속도를 높일 수 있다
• 그래디언트 소실 완화
  • 배치 정규화는 그래디언트 소실 문제를 완화해주는 효과가 있다
  • 이는 각 레이어의 활성화값이 적절한 범위에 있도록 유지해주기 때문이다
• 과적합 억제
  • 배치 정규화는 네트워크에 약간의 노이즈를 추가하여 일종의 규제 효과를 준다
  • 이는 모델의 과적합을 억제해준다
• 초기값에 덜 민감해짐
  • 배치 정규화는 각 레이어의 입력 분포를 정규화함으로써 파라미터 초기값에 대한 모델의 민감도를 줄여준다

Test Time에서의 동작

• BN에서 평균과 분산은 학습데이터에서 구한 것이다. Test time에 추가적인 계산은 하지 않는다
• Training time에 running averages 같은 방법으로 평균, 분산을 계산하고 Test time에 사용한다

Babysitting the learning Process(학습과정을 다루는 법)

Train 전

• 첫 번째는 데이터 전처리이다
  • 앞서 배운것 처럼 zero-mean을 사용한다
• 두 번째는 아키텍쳐를 선택해야 한다
• 세 번째는 네트워크 초기화이다
  • Forward pass를 하고난 후에 Loss가 그럴듯해야 한다
  • 초기 Loss가 정상인지 아닌지 확인하는 작업이다

Train 후

• 처음 시작할 때 좋은 방법은 데이터의 일부만 우선 학습시켜 보는 것이다
  • 데이터가 적으면 당연히 Overfit이 생길 것이고 Loss가 많이 줄어들 것이다
  • 이때는 regularization를 사용하지 않는다. 그리고 Loss가 내려가는지를 확인하는 것이다
  • Epoch마다 Loss가 잘 내려가는지를 보는 것이다
  • Loss가 0을 향해 꾸준히 잘 내려가는지를 확인해본다
  • Loss가 내려감과 동시에 Train Accuracy는 점점 증가한다
  • 데이터가 작은 경우라면 모델이 완벽하게 데이터를 overfit 할 수 있어야 한다
• 이제는 전체 데이터 셋을 사용할 것이고 regularization 을 약간만 주면서 적절한 learning rate를 찾아야 한다
  • Learning rate는 가장 중요한 하이퍼 파라미터 중 하나이다
  • 가장 먼저 정해야만 하는 하이퍼 파라미터이다
  • 우선 learning rate 몇 가지를 정하고 실험해 본다
  • 보통 learning rate는 1e-3 에서 1e-5 사이의 값을 사용한다
  • 이 범위 사이의 값을 이용해서 cross-validation 을 수행한다
  • 이 사이의 값들을 이용해서 learning rate가 지나치게 작은지 아니면 큰지를 결정할 수 있다

Hyperparameter Optimization(하이퍼 파리미터 최적화)

cross-validation strategy

• Cross-validation은 Training set으로 학습시키고 Validation set으로 평가하는 방법이다

첫 번째

• 우선 coarse stage 에서는 넓은 범위에서 값을 골라낸다
• Epoch 몇 번 만으로도 현재 값이 잘 동작하는지 알 수 있다
• Epoch이 많지 않아도 어떤 하이퍼파라미터가 좋은지 아닌지를 알 수 있다
• Nan이 뜨거나 혹은 Loss가 줄지 않거나 하는 것을 보면서 이에 따라 적절히 잘 조절할 수 있다
• coarse stage가 끝나면 어느 범위에서 잘 동작하겠다를 대충 알게 된다

두 번재

• fine stage에서는 좀 더 좁은 범위를 설정하고 학습을 좀 더 길게 시켜보면서 최적의 값을 찾는다
• NaNs 으로 발산하는 징조를 미리 감지할 수도 있다. Train 동안에 Cost가 어떻게 변하는 지를 살펴보는 것이다
• 이전의 cost보다 더 커지거나 한다면, 가령 이전보다 cost가 3배 높아졌다거나 하면 잘못 하고 있는 것이다
• Cost가 엄청 크고 빠르게 오르고 있다면 loop를 멈춰버리고 다른 하이퍼파라미터를 선택하면 된다
• 하이퍼 파라미터 최적화 시에는 Log scale로 값을 주는 것이 좋다
• 파라미터 값을 샘플링할때 10^-3 ~ 10^-6을 샘플링하지 말고 10의 차수 값만 샘플링하는 것이 좋다(-3 ~ -6). 왜냐하면 learning rate는 gradient와 곱해지기 때문에 learning rate의 선택 범위를 log scale을 사용하는 편이 좋다. 따라서 차수(orders of magnitude)을 이용하는 편이 좋다

grid search

• 주어진 하이퍼파라미터 값들의 모든 가능한 조합에 대해 모델을 학습시키고, 가장 좋은 성능을 보여주는 하이퍼파라미터 조합을 선택한다
• 하이퍼 파라미터를 고정된 값과 간격으로 샘플링하는 것이다
• 하지만 실제로는 grid search보다는 이전 처럼 random search를 하는 것이 더 좋다
• Random이 더 좋은 이유는 바로 내 모델이 어떤 특정 파라미터의 변화에 더 민감하게 반응을 하고 있다고 생각해 보면 이 함수가 더 비효율적인 dimentionality를 보인다고 할 수 있고 Random search는 중요한 파라미터에게도 더 많은 샘플링이 가능하므로 함수를 더 잘 찾을 수 있다
• Random search를 사용하면 important variable 에서 더 다양한 값을 샘플링 할 수 있으므로 더 좋다

출처 및 참조

https://youtu.be/wEoyxE0GP2M?si=uDXI1LG_zrb5r6mH