기계학습 수업의 기말과제는 흥미로운 주제를 선택해서 기계학습 모델링을 해보는 것이다.
내가 실습하기에 흥미로운 주제를 찾다가 2014년 월마트에서 Kaggle Competition으로 제공한 월마트 데이터셋을 바탕으로 주간 매출액을 예측하는 회귀(Regression)분석을 하기로 결정했다.
Walmart Sales Forecast - Regression
1. 주제 선정
- Base Dataset: 2014년 월마트에서 Kaggle Competition을 위해 제공한 데이터셋으로 45개 익명 매장의 2010-12년 주간 매출액과 휴일, 기온, 유가, CPI(미국 소비자 물가), 실업률, 매장 크기 정보가 포함되어 있다.
- Feature Engineering: 기존 데이터셋에서 제공하는 변수외에 가계지출과 관련있는 경제지표를 추가로 찾아보고 활용하고자 했다.
2. 데이터 수집
기본 데이터셋에 제공된 매장 크기, 실업률, 기온을 바탕으로 실제 매장을 찾아낸 후 주(State)별 평균 주급, State GDP Feature를 추가해 분석에 사용하였다.
(1) Walmart Recruiting - Store Sales Forecasting
(https://www.kaggle.com/competitions/walmart-recruiting-store-sales-forecasting/overview/)
(2) State Economic Monitor
(https://apps.urban.org/features/state-economic-monitor/)
3. 전처리 단계(Pre-processing)

# 구글 코랩으로 마운트 from google.colab import drive drive.mount('/content/drive')
# required libraries import numpy as np np.random.seed(42) import os import urllib.request import pandas as pd import matplotlib.pyplot as plt from matplotlib import pyplot import seaborn as sns import joblib from google.colab import files # machine learning libraries from sklearn.linear_model import SGDRegressor from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.model_selection import cross_val_score from sklearn.model_selection import RandomizedSearchCV from sklearn.linear_model import Ridge, Lasso from sklearn.metrics import r2_score from scipy.stats import randint # preprocessing from sklearn.model_selection import train_test_split from sklearn.model_selection import StratifiedShuffleSplit # date from datetime import date import holidays import datetime
# 데이터 불러오기 data_path = '/content/drive/MyDrive/Walmart_Store_sales.csv' # 날짜는 날짜형식으로 지정해준다. all_data = pd.read_csv(data_path, parse_dates=["Date"]) all_data_size = len(all_data) # 날짜별 분리 all_data['Year'] = all_data['Date'].dt.year all_data['Month'] = all_data['Date'].dt.month all_data['Week'] = all_data['Date'].dt.week
# 이상치 제거 def drop_outliers(df, col_name): print('Dropping outliers in ', col_name ,'...') to_keep = (df[col_name].isnull()) | ((df[col_name] < df[col_name].mean() + 3 * df[col_name].std()) & (df[col_name] > df[col_name].mean() - 3 * df[col_name].std())) df = df.loc[to_keep,:] print('Done. Number of lines remaining : ', df.shape[0]) return df for c in ['Temperature', 'Fuel_Price', 'CPI', 'Unemployment', 'WeekIncome', 'StateGDP']: all_data = drop_outliers(all_data, c) all_data.head()
4. 데이터 탐색(EDA)

- Store: 익명의 45개 매장을 1-45까지의 숫자로 표시
- City: 해당 매장이 위치한 도시명
- State: 해당 매장이 위치한 주(State)명
- Date: 매출액 수집 날짜(주 1회) - Weekly_Sales: 매장별 주간 매출액. 타겟값
- Holiday_Flag: 휴일(이벤트) 여부(크리스마스, 슈퍼볼, 블랙프라이데이 등)
- Temperature: 해당 매장이 위치한 지역의 평균 기온
- Fuel_Price: 해당 매장이 위치한 지역의 평균 유가
- CPI: 해당 State의 주간 소비자 물가 지수
- Unemployment: 해당 State의 주간 실업률
- Type: 매장 형태 (규모 순: A > B> C) - Size: 매장 크기 (단위: sq ft)
- WeekIncome: 해당 State의 평균 주급
- StateGDP: 해당 State의 분기별 GDP
- Year: 년도
- Month: 월
- Week: 주차
City, State, Date, Type, Year, Month, Week 변수는 Feature로서의 의미가 없다고 판단되거나 파생 feature를 만다는데 사용한 후 삭제된 컬럼임.
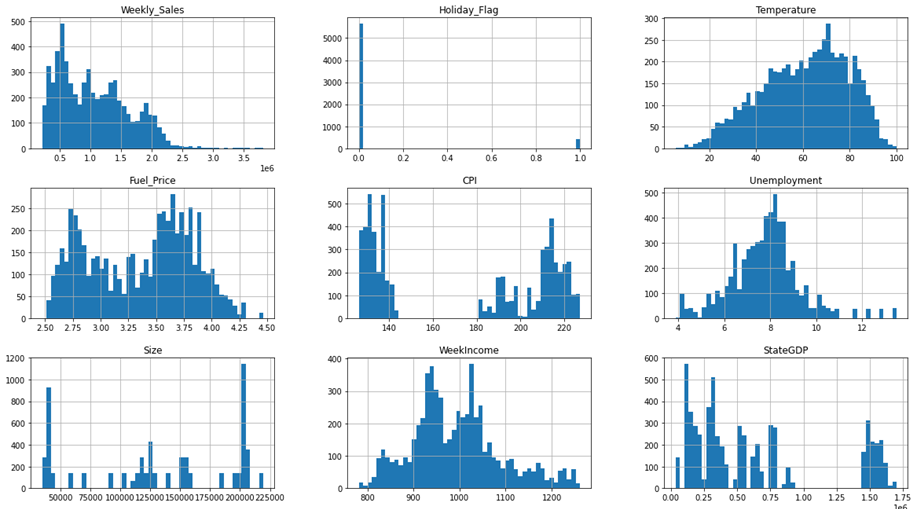
데이터셋을 확정하고 numerical feature에 대한 histogram을 만들어 시각적으로 다시 한번 확인함.
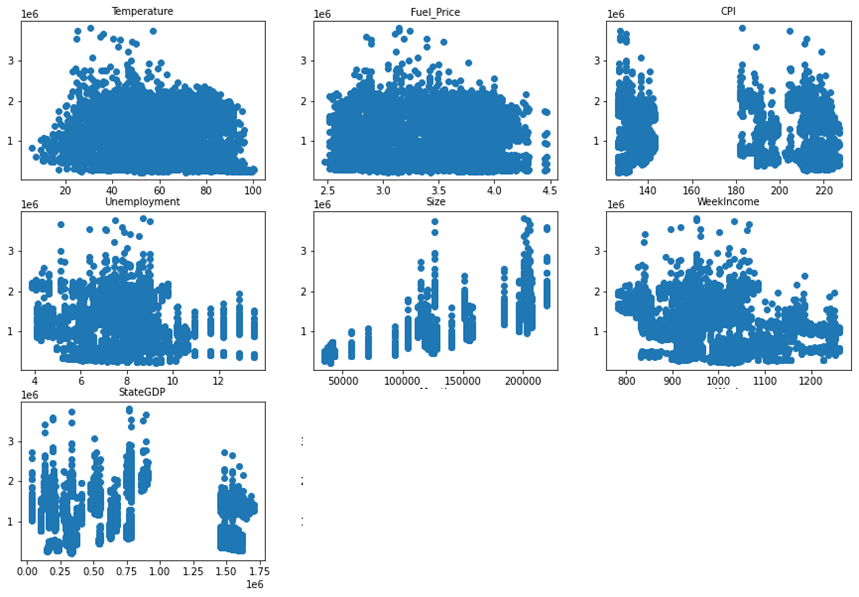
타겟값인 weekly_sales와 각 변수들을 산점도로 확인해 봤는데,
산점도로 봤을 때는 가운데 size(매장크기), month에서만 우상향하는 모습을 확인했고 나머지 attribute들은 방향을 확인하기는 어려웠다.
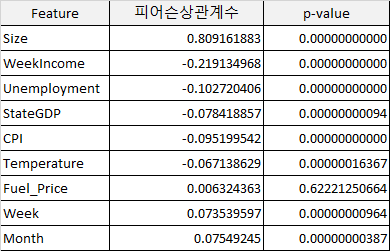
Fuel_price(유가)를 제외한 나머지 컬럼이 모두 5% 미만으로 통계적으로 유의하다는 결론을 내릴 수 있었다.
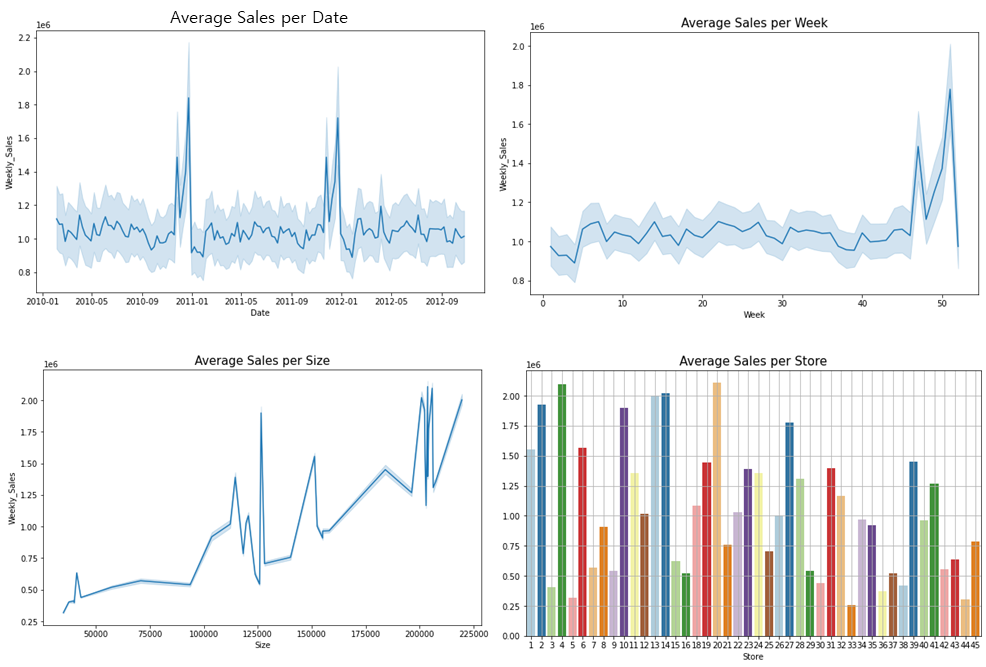
매출액과 다양한 변수들의 관계를 차트로 확인해봤는데,
- 날짜와의 관계를 보면 월마트 매출액이 매년 4분기에 폭발적으로 증가하는 것을 볼 수 있었고,
(통상적으로도 미국은 4분기에 연휴가 많아서 소비가 엄청 많은 편.) - 매장 사이즈와의 관계를 봐도 어느정도 매장 크기가 클수록 매출액도 높은 우상향을 띄고 있다.
- 45개 매장별 평균 매출은 25만불부터 200만불까지 매장마다 평균 매출액이 상이한 것을 볼 수 있다.
# 날짜별 매출 확인 plt.figure(figsize =(10, 6)) sns.lineplot(x=all_data['Date'], y= all_data['Weekly_Sales'], palette='Paired') plt.title('Average Sales per Date', fontsize=15) plt.show()
# 사이즈 별 매출 확인 plt.figure(figsize =(10, 6)) sns.lineplot(x=all_data['Size'], y= all_data['Weekly_Sales'], palette='Paired') plt.title('Average Sales per Size', fontsize=15) plt.show()
# 스토어 별 매출 확인 store_sales = all_data['Weekly_Sales'].groupby(all_data['Store']).mean() size_sales = all_data['Weekly_Sales'].groupby(all_data['Size']).mean() plt.figure(figsize=(10, 6)) sns.barplot(store_sales.index, store_sales.values, palette="Paired") plt.grid() plt.title('Average Sales per Store', fontsize=15) plt.show()
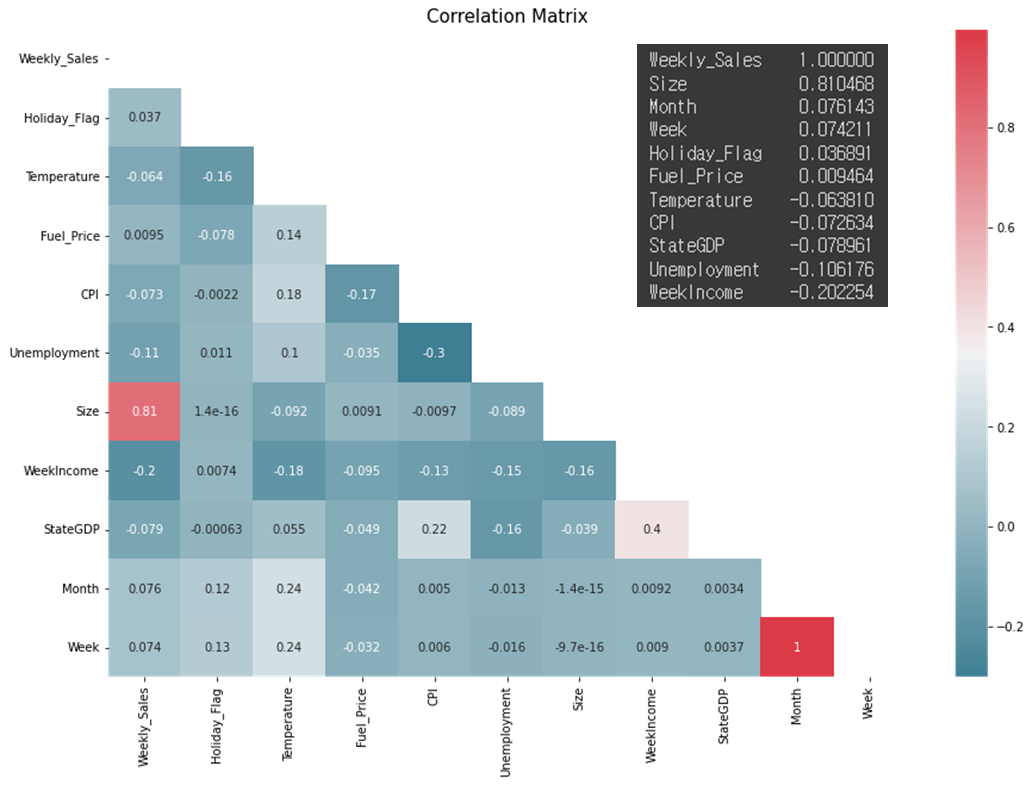
각 속성들의 상관관계를 Correlation Matrix로도 확인해 봤는데
타겟값인 weekly_sales와는 Size과 정비례, 나머지는 수치가 그리 높진 않지만 주급 & 실업률 & StateGDP와 반비례하는 것을 볼 수 있다.
# 상관관계 확인 s = pd.DataFrame(corr) s = s['Weekly_Sales'].sort_values(ascending=False) s.columns = ['feature', 'corr']
# Correlation Matrix 만들기 plt.figure(figsize=(15, 10)) plt.title('Correlation Matrix', fontsize = 15) mask = np.zeros_like(corr, dtype=np.bool) mask[np.triu_indices_from(mask)] = True sns.heatmap(corr, cmap = sns.diverging_palette(220, 10, as_cmap=True), annot=True, mask=mask) plt.show()
5. 데이터 모델링 준비
(5-1). 타겟값(y)와 나머지 features(X)를 분리
X = dataset[[c for c in dataset.columns if c not in ['Weekly_Sales']]] y = dataset['Weekly_Sales']
(5-2) dataframe을 array로 변환
np.set_printoptions(formatter={'float_kind': lambda x: "{0:0.2f}".format(x)}) X = X.values y = y.to_numpy() print(X[0,:]) print() print(y[0:5])
(5-3) Test/Train Set Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = 42) print("X_train: ", X_train.shape), print("y_train: ", y_train.shape) print("X_test: ", X_test.shape), print("y_test: ", y_test.shape)
(5-4) 스케일링 (standard Scaler)
scaler = StandardScaler() scaler.fit(X_train) X_scaled = scaler.transform(X_train) X_test_scaled = scaler.transform(X_test) print(X_scaled[:1]) print("----------------") print(X_test_scaled[:1])
(5-5) RMSE 확인
예측한 값과 실제 환경에서 관찰되는 값의 차이를 나타낸다.
MSE보다 큰 오류값 차이에 대해 크게 패널티를 주는 이점이 있다.
lin_reg = LinearRegression() lin_reg.fit(X_scaled, y_train) some_data = X_scaled[:5] some_labels = y_train[:5] print("Predictions:", lin_reg.predict(some_data)) print("Labels:", list(some_labels))
6. 모델링
나는 7개의 모델로 학습하였고
학습결과를 결정계수인 R2값으로 성능을 평가하였다.
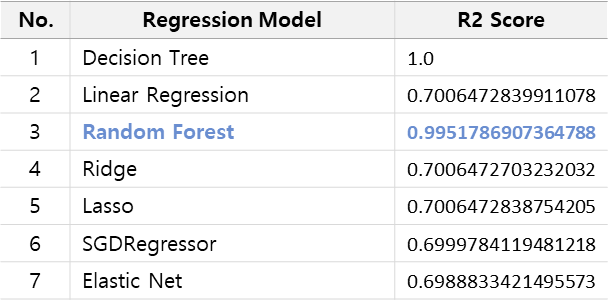
결론을 미리 말하면 Random Forest에서 가장 높은 성능을 보임을 확인하였다.
Decision Tree는 Overfitting이라고 판단되어 선정에서 제외했다.
(6-1) Decision Tree
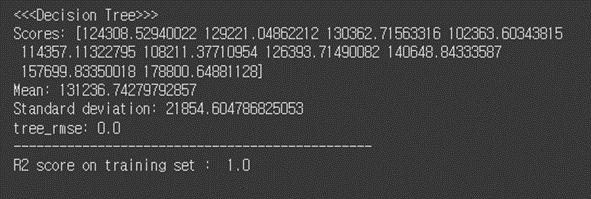
# 1. Decision Tree tree_reg = DecisionTreeRegressor(random_state=42) tree_reg.fit(X_scaled, y_train) # tree_predictions = tree_reg.predict(X_scaled) tree_mse = mean_squared_error(y_train, tree_predictions) tree_rmse = np.sqrt(tree_mse) # from sklearn.model_selection import cross_val_score scores = cross_val_score(tree_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) tree_rmse_scores = np.sqrt(-scores) # def display_scores(scores): print("Scores:", scores) print("Mean:", scores.mean()) print("Standard deviation:", scores.std()) # print("<<<Decision Tree>>>") display_scores(tree_rmse_scores) print("tree_rmse:", tree_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, tree_predictions))
(6-2) Linear Regression
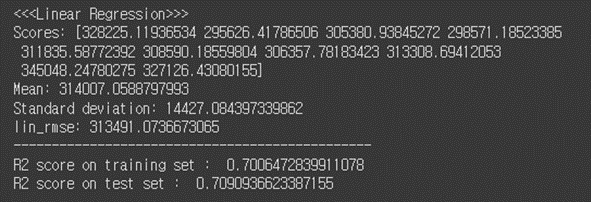
# 2. Linear Regression lin_reg = LinearRegression() lin_reg.fit(X_scaled, y_train) # #training lin_predictions = lin_reg.predict(X_scaled) lin_mse = mean_squared_error(y_train, lin_predictions) lin_rmse = np.sqrt(lin_mse) # #test lin_test_predictions = lin_reg.predict(X_test_scaled) lin_test_mse = mean_squared_error(y_test, lin_test_predictions) lin_test_rmse = np.sqrt(lin_test_mse) # scores = cross_val_score(lin_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) lin_rmse_scores = np.sqrt(-scores) # print("<<<Linear Regression>>>") display_scores(lin_rmse_scores) print("lin_rmse:", lin_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, lin_predictions)) print("R2 score on test set : ", r2_score(y_test, lin_test_predictions))
(6-3) Random Forest
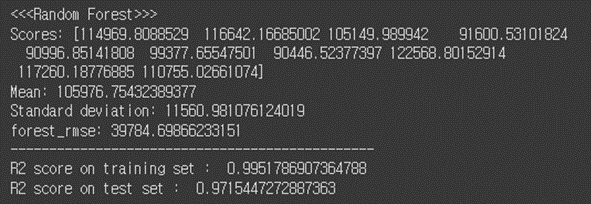
# 3. Random Forest forest_reg = RandomForestRegressor(n_estimators=100, random_state=42) forest_reg.fit(X_scaled, y_train) # forest_predictions = forest_reg.predict(X_scaled) forest_mse = mean_squared_error(y_train, forest_predictions) forest_rmse = np.sqrt(forest_mse) # #test forest_test_predictions = forest_reg.predict(X_test_scaled) forest_test_mse = mean_squared_error(y_test, forest_test_predictions) forest_test_rmse = np.sqrt(forest_test_mse) # forest_scores = cross_val_score(forest_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) forest_rmse_scores = np.sqrt(-forest_scores) # print("<<<Random Forest>>>") display_scores(forest_rmse_scores) print("forest_rmse:", forest_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, forest_predictions)) print("R2 score on test set : ", r2_score(y_test, forest_test_predictions))
(6-4) Ridge
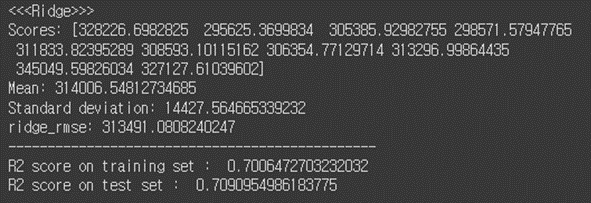
# 4. Ridge ridge_reg = Ridge(alpha=0.1, solver="cholesky") ridge_reg.fit(X_scaled, y_train) # ridge_predictions = ridge_reg.predict(X_scaled) ridge_mse = mean_squared_error(y_train, ridge_predictions) ridge_rmse = np.sqrt(ridge_mse) # #test ridge_test_predictions = ridge_reg.predict(X_test_scaled) ridge_test_mse = mean_squared_error(y_test, ridge_test_predictions) ridge_test_rmse = np.sqrt(ridge_test_mse) # ridge_scores = cross_val_score(ridge_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) ridge_rmse_scores = np.sqrt(-ridge_scores) # print("<<<Ridge>>>") display_scores(ridge_rmse_scores) print("ridge_rmse:", ridge_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, ridge_predictions)) print("R2 score on test set : ", r2_score(y_test, ridge_test_predictions))
(6-5) Lasso
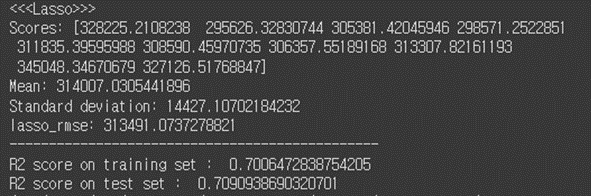
# 5.Lasso lasso_reg = Lasso(alpha=0.1) lasso_reg.fit(X_scaled, y_train) # lasso_predictions = lasso_reg.predict(X_scaled) lasso_mse = mean_squared_error(y_train, lasso_predictions) lasso_rmse = np.sqrt(lasso_mse) # #test lasso_test_predictions = lasso_reg.predict(X_test_scaled) lasso_test_mse = mean_squared_error(y_test, lasso_test_predictions) lasso_test_rmse = np.sqrt(lasso_test_mse) # lasso_scores = cross_val_score(lasso_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) lasso_rmse_scores = np.sqrt(-lasso_scores) # print("<<<Lasso>>>") display_scores(lasso_rmse_scores) print("lasso_rmse:", lasso_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, lasso_predictions)) print("R2 score on test set : ", r2_score(y_test, lasso_test_predictions))
(6-6) SGD Regressor
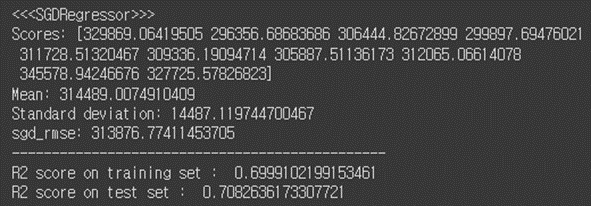
# 6.SGDRegressor sgd_reg = SGDRegressor(penalty="l2") #sgd_reg = SGDRegressor(max_iter=1000, tol=0.001, penalty="l2", eta0=0.1) sgd_reg.fit(X_scaled, y_train) # sgd_predictions = sgd_reg.predict(X_scaled) sgd_mse = mean_squared_error(y_train, sgd_predictions) sgd_rmse = np.sqrt(sgd_mse) # #test sgd_test_predictions = sgd_reg.predict(X_test_scaled) sgd_test_mse = mean_squared_error(y_test, sgd_test_predictions) sgd_test_rmse = np.sqrt(sgd_test_mse) # sgd_scores = cross_val_score(sgd_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) sgd_rmse_scores = np.sqrt(-sgd_scores) # print("<<<SGDRegressor>>>") display_scores(sgd_rmse_scores) print("sgd_rmse:", sgd_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, sgd_predictions)) print("R2 score on test set : ", r2_score(y_test, sgd_test_predictions))
(6-7) Elastic Net
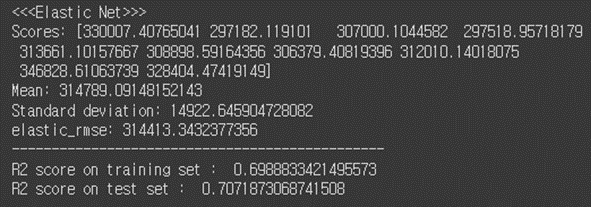
# 7. Elastic Net from sklearn.linear_model import ElasticNet # elastic_reg = ElasticNet(alpha=0.1, l1_ratio=0.5) elastic_reg.fit(X_scaled, y_train) # elastic_predictions = elastic_reg.predict(X_scaled) elastic_mse = mean_squared_error(y_train, elastic_predictions) elastic_rmse = np.sqrt(elastic_mse) # #test elastic_test_predictions = elastic_reg.predict(X_test_scaled) elastic_test_mse = mean_squared_error(y_test, elastic_test_predictions) elastic_test_rmse = np.sqrt(elastic_test_mse) # elastic_scores = cross_val_score(elastic_reg, X_scaled, y_train, scoring="neg_mean_squared_error", cv=10) elastic_rmse_scores = np.sqrt(-elastic_scores) # print("<<<Elastic Net>>>") display_scores(elastic_rmse_scores) print("elastic_rmse:", elastic_rmse) print("-----------------------------------------------") print("R2 score on training set : ", r2_score(y_train, elastic_predictions)) print("R2 score on test set : ", r2_score(y_test, elastic_test_predictions))
7. 평가 및 예측 결과
학습했던 7개의 모델 중 Random Forest를 최종 선정한 후 해당 모델을 피클파일에 저장해 테스트 데이터에 예측해 보았다.
(7-1) 모델 저장 (피클)
reg = RandomForestRegressor(n_estimators=100, random_state=42).fit(X_scaled, y_train) # # 피클 파일로 저장 ```python joblib.dump(reg, 'reg.pkl', compress=1)
(7-2) 테스트 데이터로 평가 결과
# Evaluation loaded_model = joblib.load('./reg.pkl') # score = loaded_model.score(X_test_scaled, y_test) print('test score: {score:.3f}'.format(score=score))
test score: 0.972
테스트 데이터로 평가한 결과 0.972로 역시나 높은 성능을 보였다!
스코어가 지나치게 높게 나왔다는 의심(?)을 지울 수 없지만 train, test에서 둘 다 비슷하게 높은 점수를 받아 따로 튜닝을 하지는 않았다.
(7-3) 실제 매출액 예측하기
위에서 만든 Random Forest 모델을 사용하여 test set에 있던 1,215개의 매장 주간 매출액을 예측해 보았다.

정상적으로 예측됨을 확인!
df = pd.DataFrame(X_test, columns = ['Store', 'Holiday_Flag', 'Temperature', 'Fuel_Price', 'CPI', 'Unemployment', 'Size', 'WeekIncome', 'StateGDP', 'Month', 'Week']) # predictions = reg.predict(X_test_scaled) df['Weekly_Sales'] = predictions # # 소수점 2자리로 매출액 표시 pd.options.display.float_format = '{:.2f}'.format df
Regression 분석을 처음부터 끝까지 해본건 처음이라
생각보다 시간이 많이 소요되었다. (퇴근하고 평일 5일 저녁 내내 붙잡고 있었던 듯 하다.)
따로 튜닝을 할 필요없이 한번에 너무 좋은 결과가 나와서 이래도 되나 싶긴한데...
Kaggle에 기본 Dataset으로 회귀분석한 다른 사례를 보니 최고 점수(R2)가 92%인걸 보면
(https://www.kaggle.com/code/pierrelouisdanieau/walmart-sales-forecasting)
내가 고생해서 찾아 넣은 StateGDP와 WeekIncome이 학습에 큰 영향을 준 듯 하다.
A-Z까지 전체 다 해봤으니 다음 분석은 좀 수월하지 않을까?

실제 매장 위치를 어떻게 찾아내셨는지 구체적으로 알 수 있을까요 ??