다양한 Loss에 대해 알아보자

용가리·2025년 4월 14일

반갑습니다
이번 글에서는 다양한 Loss(손실함수)들의 종류와 쓰임새에 대한 글을 작성해보겠습니다.

손실함수란?

손실함수(목적함수)란, 모델의 예측값과 실제 정답간의 차이를 수치로 나타내는 함수입니다.
계산된 Loss는 역전파를 통해 모델의 파라미터들에 전달되고, 이는 경사하강법에 사용되어 모델의 학습을 진행시킵니다.

왜 목적함수(Objective Function)이라고도 불릴까요?
제 생각에는 모델 학습에 대한 목적을 가장 크게 담고 있는 함수이기 때문인 듯 합니다.
만약 본인의 모델이 분류를 잘 하도록 학습시키고 싶다면 예측과 정답의 차이가 클 수록 패널티를 강하게 부여하는 손실 함수를 사용하고, 유사한 데이터끼리를 묶고 싶다면 유사도가 적을 수록 패널티를 강하게 부여하는 손실함수를 사용하게 되겠죠.

이렇듯 모델의 쓰임새, 학습의 목적을 가장 잘 나타내는 함수가 손실함수입니다.
다양한 손실함수를 알고 있다면 낯선 모델의 구조를 접했을 때 손실함수를 통해 모델이 어떤 역할을 하기 위해 학습됐는지에 대해 알 수 있습니다.

손실함수의 종류

손실함수는 그 목적이 회귀인지, 분류인지 등에 따라 종류가 나뉠 수 있습니다.

회귀를 위한 Loss

1. MSE Loss

$Loss = \displaystyle\frac{1}{n}\sum_{i=0}^{n}{(y_i-y_{hat})^2}$
기본적인 로스의 형태입니다.
예측값과 실제값의 차를 제곱한 값들의 평균을 Loss로 활용합니다.
가장 직관적인 형태이지만, 이상치에 민감하다는 단점이 있습니다.
제곱을 하기에 Loss값이 엄청 커질 수 있기 때문이죠.
또한 제곱되어 표현되기 때문에 기존 데이터와 단위가 달라 해석이 어렵다는 단점이 존재합니다.

2. MAE Loss

$Loss = \displaystyle\frac{1}{n}\sum_{i=0}^{n}|y_i - y_{hat}|$
실제값과 예측값의 차의 절대값들의 평균을 Loss로 활용합니다.
데이터의 단위가 동일해 직관적 해석이 가능하다는 장점이 있습니다.
이상치에 영향을 덜 받는다는 장점도 있죠.
또, 오차의 가중치가 같습니다.
하지만 미분 불가능한 점(오차가 0인 점)이 존재한다는 단점이 존재합니다.

3. RMSE Loss

$\text{Loss} = \frac{1}{n}\sqrt{{\sum_{i=0}^{N - 1} (y_i - \hat{y}_i)^2}}$
MSE Loss에 제곱근을 씌운 형태입니다.
MSE Loss에 비해 이상치에 덜 민감하다는 장점이 있습니다. (그래도 민감합니다.)
또한, 기존 데이터 단위와 동일해 직관적 해석이 가능하다는 장점이 있습니다.
-1~1 사이를 벗어날 수록 오차의 가중치가 커진다는 특징이 있습니다.

'
'
'
이렇게 대표적인 세가지 Loss를 비교해 볼 때, MSE는 이상치에 아주 민감하며, 해석이 어렵고, RMSE는 MSE에 비해 이상치에 덜 민감하며 데이터의 단위가 같아 해석이 용이하다는 특징이 있으며, MAE는 데이터의 단위가 같고 오차의 가중치가 동일하다는 특징이 있겠습니다.

이상치에 대해 민감하게 반응하는 모델을 만들고 싶다면 MSE나 RMSE를, 좀 더 이상치에 강건한 모델을 만들고 싶다면 MAE를 사용하면 좋겠군요.

4. Huber Loss

$L_\delta(y, \hat{y}) = \begin{cases} \frac{1}{2}(y - \hat{y})^2 & \text{if } |y - \hat{y}| \leq \delta \\ \delta \cdot (|y - \hat{y}| - \frac{1}{2} \delta) & \text{otherwise} \end{cases}$

Huber Loss 는 MAE Loss와 MSE Loss의 단점들을 보완하기 위해 고안된 Loss입니다.
MAE Loss는 미분 불가능한 점이 존재한다는 단점, MSE Loss는 이상치에 대해 큰 Loss를 갖는다는 단점이 존재합니다.
수식을 살펴보면 $\delta$ 를 통해 이상치에 대해 어떻게 반응할지 직접 설정할 수 있습니다.
다양한 Case에 좀 더 유연하게 대응할 수 있는 Loss라고 생각하시면 좋을 것 같습니다.

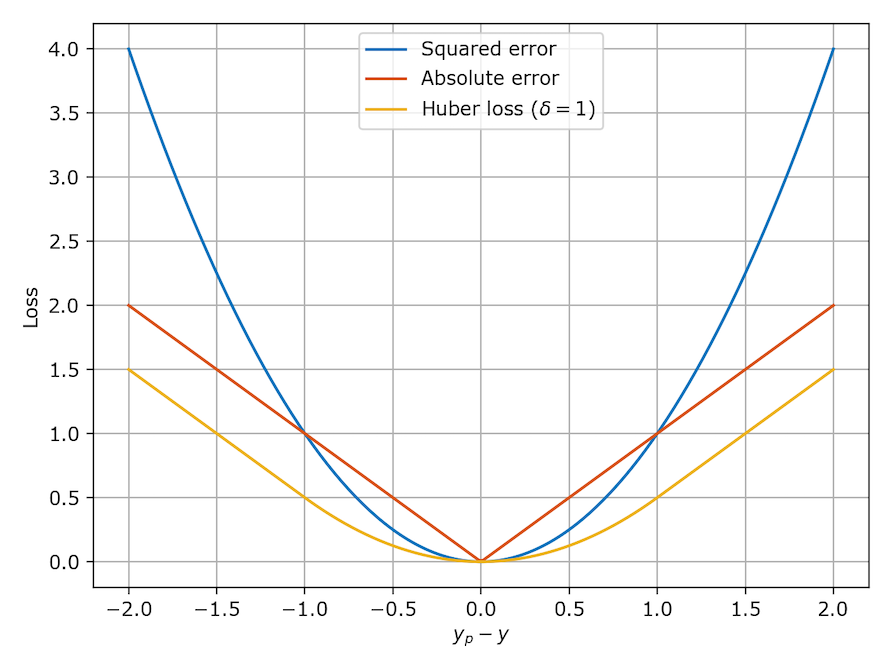
사진을 보면 Huber Loss는 전 구간에서 미분이 가능하며, 1이 넘어갈 수록 급격히 Loss가 올라가지 않는 모습을 살펴볼 수 있습니다.

분류를 위한 Loss

5. Binary Cross Entropy Loss

$L_{\text{BCE}}(y, \hat{y}) = - ( y \cdot \log(\hat{y}) + (1 - y) \cdot \log(1 - \hat{y}))$

BCE Loss는 이진 분류에서 사용되는 Loss입니다.
개냐 고양이냐 / 사람이냐 사람이 아니냐 / 비속어냐 비속어가 아니냐 등 다양한 이진 분류에 사용되는 Loss입니다.

BCE Loss에도 단점이 존재하는데

클래스 불균형 문제가 발생할 경우(라벨이 1 데이터가 99개, 0 데이터가 1개) 모델이 전부 1로 예측해도 된다고 판단하여 학습이 제대로 이루어지지 않는 경우가 존재합니다. 이럴 경우 클래스 불균형 문제를 해소하거나 희소 라벨의 Class Weight를 올리거나 맞추기 쉬운 문제의 Loss를 낮게, 어려운 문제의 Loss를 높게 가져가는 Focal Loss를 사용하여 해결할 수 있습니다.
BCE Loss는 수식에서 알 수 있듯이, $y$ 와 $\hat{y}$ 이 0~1사이의 확률값이라는 가정 하에 Loss를 계산합니다.
0과 1 사이의 확률값을 얻기 위해 보통 신경망의 끝단에 Sigmoid 함수를 통과시키게 되는데, 만약 정답이 0인 Class를 0.99로 예측하거나, 정답이 1인 Class를 0.01이라고 예측하는 등 높은 Confident를 가지고 잘못 예측하게 된다면 Backpropagation 과정에서 Loss가 아주 큼에도 불구하고 Sigmoid의 기울기가 0으로 수렴해 학습이 제대로 되지 않는 Gradient Saturation 문제가 발생합니다.
$σ^′ (x)=σ(x)(1−σ(x))$ 의 식에서 $σ(x)$ 가 0이나 1이라고 생각하면 이해가 쉬울 듯 싶습니다.
이러한 문제는 BCEWithLogitsLoss(내부적으로 Sigmoid와 BCE Loss를 함께 처리), Batch Norm, Weight initialization 등의 방법으로 수치적 안정을 고려하면 해결할 수 있습니다.

6. Categorical Cross Entropy Loss

$L_{\text{CCE}}(y, \hat{y}) = - \sum_{c=1}^{C} y_c \cdot \log(\hat{y}_c)$

Categorical Cross Entropy Loss는 다중 클래스의 분류를 위한 Loss 함수입니다.
(참고 : Pytorch의 nn.CrossEntropyLoss()는 Softmax + Cross Entropy Loss로 구현돼 있습니다. 입력으로 Logit을 넣으면 Loss가 나오도록 설계한 것이지요.)

만약 Class의 수가 2개라면, Binary Cross Entropy와 동일한 수식이 됩니다.
그렇기에 BCE Loss와 단점을 어느정도 공유합니다.

Log 확률을 사용하기에 0과 1에서 불안정한 면이 있죠.
이 부분은 BCE Loss와 비슷한 대처법을 사용하거나, Label Smoothing 이라는 것을 사용하여 극단적인 예측을 예방합니다. 클래스간 라벨 분포를 보다 부드럽게 바꿔주자는 개념이죠. Temperature 수식을 생각하시면 되겠습니다.
Label간의 연관성에 대해 고려하지 않습니다.
가령 0,1,2의 클래스가 개, 고양이, 호랑이 라면 같은 고양이과인 고양이와 호랑이를 전혀 다른 Class로 판단한다는 의미입니다. 이 경우 , Semantic Smoothing이라는 기법을 통해 어느정도 해소할 수 있습니다. Label Smoothing과 비슷한데, 비슷한 것 끼리는 Smoothing 수치를 다르게 적용하는 기법입니다.
고양이가 정답일 때→ '호랑이': 0.2, '개': 0.05 이렇게 가중치를 부여합니다.

7. Negative Log Likelihood Loss

$L_{\text{NLL}}(y, \hat{y}) = - \log(\hat{y}_{y})$

Negative Log Likeligood Loss는 Categorical Cross Entropy Loss와 유사합니다. 후자는 Raw한 Logit을 받아 Loss로 계산하고, NLL Loss는 확률값을 받아 Loss를 계산합니다.
주로 Softmax + 뭔가의 처리 + NLL Loss의 조합으로 사용하곤 합니다.
Custom Loss를 만들 때 유용하게 사용됩니다.
이렇게 보면 거의 비슷한데 왜 이름이 다르냐
저도 잘은 모르지만 ..
'Entropy'라는 개념은 물리학 출신 용어이고 ... 'Likelihood(우도)'는 통계학 출신 용어라고 알고 있습니다.
아무튼 NLL Loss는 Cross Entropy 시리즈와 거의 유사하기에 단점과 단점에 대한 대처법 또한 동일합니다.

거리기반 Loss

거리기반 Loss는 주로 언어모델의 학습에 사용되는 목적함수입니다.
차근차근 알아보겠습니다.

8. Contrastive Loss

$\mathcal{L} = \begin{cases} ||f(x_1) - f(x_2)||^2, & \text{if } y = 1 \\ \max(0, m - ||f(x_1) - f(x_2)||)^2, & \text{if } y = 0 \end{cases}$

9. Triplet Loss

$\mathcal{L} = \max\left( 0, \; ||f(a) - f(p)||^2 - ||f(a) - f(n)||^2 + \alpha \right)$

이 두 가지는 개념이 비슷합니다.
예측 벡터를 정답 벡터와 같아지도록 합니다.
이중 Contrastive Loss는 정답 벡터와 예측 벡터의 거리가 멀 수록 Loss가 커지고, 가까울수록 작아집니다.
Triplet Loss는 방향성은 Contrastive Loss와 같으나 정답과 예측 사이의 Anchor를 둡니다. 이 Anchor는 Positive와는 가까워지도록, Negative와는 멀어지도록 기준을 잡는 데에 그 역할이 있습니다.

Contrastive Loss는 샘플 두 개의 관계만 보고 Loss를 계산하는 반면, Triplet Loss는 Positive와 Negative간의 관계를 전부 고려해서 Loss를 계산한다는 차이점이 있습니다.

얼핏 보면 Triplet Loss가 더 좋아보일 수 있지만, Anchor를 선정하는 기준을 섬세하게 정하지 않으면 오히려 모델의 성능이 떨어질 수 있겠습니다.

Anchor는 배치 내에서 랜덤하게 결정하기도 하고,
Hard Negative (Anchor와 가까운데 다른 클래스)를 선정하기도 하는데, 너무 어려우면 오히려 학습이 잘 안되기도 해서
Semi-Hard Negative(Anchor와 Negative의 거리는 Positive보다 크지만, margin보다 작음)를 찾아 결정하기도 합니다.

'
'
'
이렇게 다양한 Loss에 대해 알아봤습니다.
Loss 함수는 본인이 어떤 개념을 적용시키느냐에 따라 달라질 수 있습니다.
Class간 Weight를 조절할 수도 있고, L1, L2와 같은 Regularization을 적용할 수도 있죠.
또 L1, L2 Regularization들도 단점이 있어서, ORPO와 같은 더 발전된 규제 방법을 사용하기도 합니다.

가장 중요한 것은 본인이 풀고자 하는 목적에 최적화된 Loss를 선정하고 실험을 통해 입증하는 과정이겠네요.

저도 많은 지식을 익혀 다양한 해결책을 찾는 역량을 늘리도록 해야겠습니다.
긴 글 읽어주셔서 감사합니다 !