두 모집단의 비교

---

자료 수집 방법

---

1. 독립표본 : 실험 대상을 임의로 두 개의 그룹으로 나누고 각각의 그룹에 A,B 다른 방법을 적용하여 그 실험 결과를 비교
   ex) 남자와 여자의 1년 다이어트 후 평균 몸무게 차이
2. 대응표본(짝비교) : 비슷한 조건을 가진 실험군을 하나의 쌍으로 묶고 하나에는 A, 나머지 하나는 B로 하여 A와 B의 차이를 각각의 변수로 이용(두 실험대상은 독립이 아님)
   ex) 다이어트 전후의 몸무게 차이

• 두개의 차이는 독립표본의 경우 각각의 평균의 차이를 구하는 것이지만 대응표본은 각각의 차이의 평균을 구한다는 점에서 성질이 다르다
  

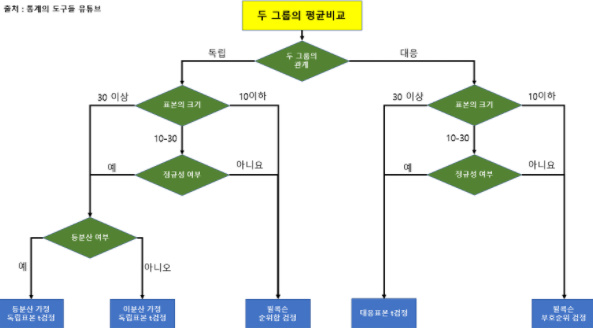
자료수집

---

• $X_1,X_2...X_n$은 평균이 $\mu_1$이고 분산이 $\sigma_1^2$인 모집단에서 임의추출한 자료
• $Y_1,Y_2... Y_n$은 평균이 $\mu_2$이고 분산이 $\sigma_2^2$인 모집단에서 임의추출한 자료
• $\overline{X} = \frac{1}{n_1}\sum X_i$ , $s_1^2 = \frac{1}{n_1-1}\sum (X_i-\overline{X})^2$
  $\overline{Y} = \frac{1}{n_2}\sum Y_i$ , $s_2^2 = \frac{1}{n_2-1}\sum (Y_i-\overline{Y})^2$

독립표본방법

---

표본의 크기가 클때

---

• $\overline{X}$~$N(\mu_1,\frac{\sigma_1^2}{n_1})$, $\overline{Y}$~$N(\mu_2,\frac{\sigma_2^2}{n_2})$
• 두 표본은 독립이기에 $\overline X-\overline Y$~$(\mu_1-\mu_2,\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2})$
• $\frac{(\overline X - \overline Y)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$ ~ $N(0,1)$

신뢰구간

---

• $(\overline X- \overline Y) \pm z_{a/2}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}$

가설검정

---

• $H_0 : \mu_1-\mu_2 = a$
• $Z = \frac{(\overline X - \overline Y)-a}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$
• 이후는 기존의 z분포에서 구하는 것과 동일함

표본의 크기가 작을때

---

• CLT를 적용할 수 없기에 더 많은 조건이 필요하다

가정

---

• 정규성 : 두 모집단은 정규분포를 따라야함
• 등분산성 : 두 모집단은 표준편차가 같음
• 정규성 확인방법 : 정규확률 그림을 그린다
• 등분산성 확인방법 : 두 표본표준편차가 $\frac{1}{2}\leq\frac{s_1}{s_2}\leq2$인지 확인

공통분산의 합동추정량

---

• 두 모집단의 분산이 같다는 가정이므로 공통분산을 추정가능
• $s_p^2 = \frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}$

신뢰구간

---

• $\frac{(\overline X - \overline Y)-(\mu_1-\mu_2)}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$ ~ $t(n_1+n_2-2)$

• $(\overline X - \overline Y) \pm t_{a/2}(n_1+n_2-2)s_p\sqrt{{\frac{1}{n_1}+\frac{1}{n_2}}}$

만약 분산이 같지 않다면?
합동추정량 $s_p^2$을 구하지 못함
따라서 $\frac{(\overline X - \overline Y)-(\mu_1-\mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}$~$t(n^*)$ 여기서 $n^*$는 $min(n_1-1,n_2-1)$이다

짝비교

---

• 실험결과가 실험에 대한 조건 이외에 다른 요인들의 영향도 맏을 수 있기에 그러한 요인들을 배제해야함
• 따라서 실험 결과에 영향을 미칠만한 다른 요인들은 비슷한 조건을 가지도록 비슷한 실험군끼리 2개씩 짝지음
  ex) 약물의 효과를 보기위해 20대 남자는 20대 남자끼리 30대 여자는 30대 여자끼리 짝지어 그 차이를 비교한다.
• 각각의 $X_1$과 $Y_1, X_2, Y_2$를 짝지어 그 차이인$D_1,D_2$를 구한다
• $\overline{D}=\frac{1}{n}\sum D_i$ , $S_D^2 = \frac{1}{n-1}\sum(D_i-\overline D)^2$

표본의 크기가 클때

---

• $\frac{\overline D-\delta}{s_D/\sqrt n}$~$N(0,1)$

신뢰구간

---

• $\overline D\pm z_{a/2}\frac{s_D}{\sqrt n}$

표본의 크기가 작을 때

---

• $\frac{\overline D-\delta}{s_D/\sqrt n}$~$t(n-1)$

신뢰구간

---

• $\overline D\pm t_{a/2}(n-1)\frac{s_D}{\sqrt n}$