정규모집단에서의 추론(표본의 크기가 작을 때)

---

t분포

---

성질

---

• 독립된 두 집단의 평균의 유의미한 차이가 있는지를 검사한다
• 일반적으로 $n\leq30$ 즉 적은 수의 표본에 대해 사용한다. / 표본이 많으면 정규분포를 사용하면된다.
• 모집단의 표준편차($\sigma$)를 모를 때 사용한다.
• 자유도가 증가할수록 표준정규분포에 가까워진다(자유도가 30이 넘으면 CLT에 의해 표준정규분포에 가까워진다.

t분포 공식

---

• $X_1,X_2...$가 정규모집단 $X(\mu,\sigma^2)$에서 임의추출한 표본일때
• $\frac{\overline{x}-\mu} {\sigma/\sqrt{n}}$~$N(0,1)$
  $\frac{\overline{x}-\mu} {\sigma/\sqrt{n}}$~$t(n-1)$인 t분포($\sigma$를 모를경우 $s$로 대체)
• p-value를 이용한 추론방식은 z-분포와 동일하다고 볼 수 있다

카이제곱분포

---

• 앞선 t분포는 모평균추론이라면 카이제곱분포는 모표준편차를 추론하기 위한 것이다.
• 쉽게 말해서 $x^2$ 분포인데 다른 분포와 달리 자료의 분포를 표현하는게 아니라 자료의 분산의 정도를 분포로 보여주는 것이다.
• $X_1,X_2..$를 임의추출하였다면 $\frac{\sum{(X_i-\overline{X})}^2}{\sigma^2}=\frac{(n-1)s^2}{\sigma^2}$~$X^2(n-1)$ 자유도가 n-1 인 카이제곱분포
• 위 식을 보아도 이전에 마주한 (표본평균-모평균)과 달리 분산에 대한 식임을 알 수 있다.
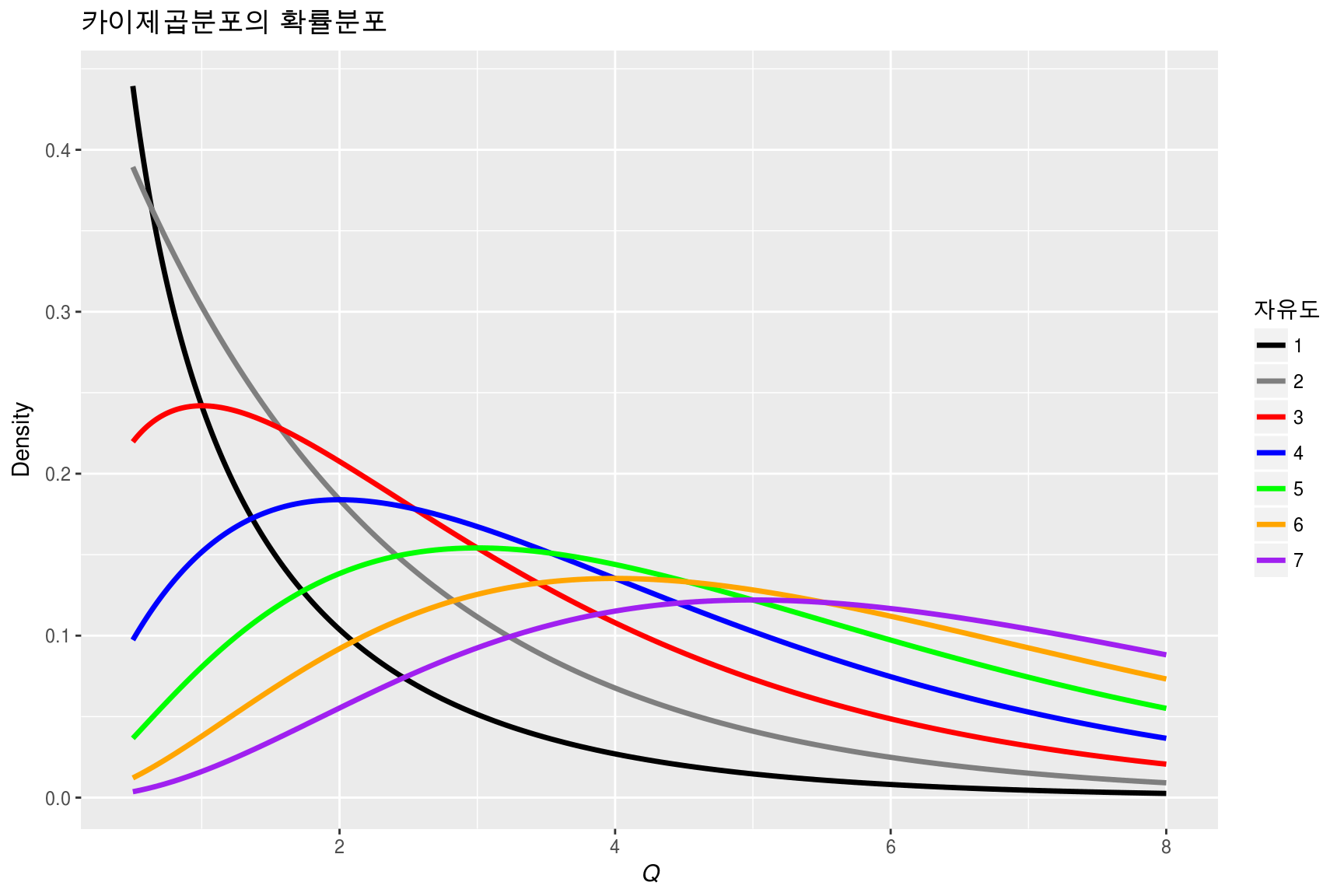
• 양수값을 가지며(제곱하기때문) 오른쪽으로 긴 꼬리를 갖는 비대칭적 확률분포
• 자유도가 클수록 더 넓게 분포함
  
• 신뢰구간은 $P(\frac{(n-1)s^2}{x^2_{a/2}(n-1)}\leq\sigma^2\leq\frac{(n-1)s^2}{x^2_{1-a/2}(n-1)})$
  위의 식에서 유도하면된다.