- 둘 이상의 변수 간의 관계를 보여주는 통계적 방법
- 독립변수(X) : 다른 변수에 영향을 주는 변수
- 종속변수() : 다른 변수의 영향을 받는 변수
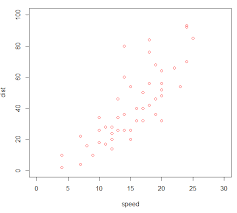
산점도
- 두 변수 사이의 연관성을 살펴볼 수 있는 그림
단순선형회귀분석
- 하나의 독립변수와 하나의 종속변수 사이의 회귀직선을 추론하는 방법을 단순선형회귀분석이라고 한다.
- 를 회귀방적식이라 나타내고 여기서 x가 여러개 될 경우 다중회귀분석이라고 한다.
- 을 회귀계수라고 하고 이러한 회귀계수를 결정하고 회귀곡선을 도출하는 과정을 회귀곡선의 추정이라고 한다.
이상적인 값으로는 모든 점들이 를 만족하고 한 직선위에 있는 것이지만 실제 값들은 모두 직선위에 있지 못하고 벗어나게 된다. 따라서 실측값에 대한 방정식은 으로 여기서 은 오차항을 나타낸다 이를 독립적인 확률변수처럼 생각할 수 있는데 ~으로 나타낼 수 있다.
최소제곱추정법
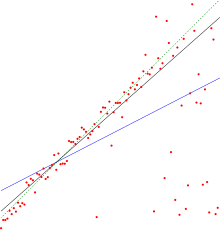
- 회귀곡선을 그리게 되면 위 그림처럼 하나의 분포에도 여러개의 직선을 얻을 수 있다.
- 하지만 이렇게 많은 직선들중 가장 적합한 직선을 구해야 하는데 적합한 직선이라하면 관찰값에 가장 근접한 직선이라 말할 수 있고 이는 분산이 가장 적은 모형이라 말할 수 있다.
- 이러한 직선을 구할 때 사용하는 것이 최소제곱추정법이라 말할 수 있고 가 최소가 되는 을 찾으면 되는 것이다.
- 이렇게 최소가되는 을 이용하여 구한 직선을 추정회귀직선이라하고 로 나타낸다.
정규방정식
- 최소제곱추정법을 쉽게 풀기 위해서는 정규방정식이라는 것을 이용하는데 추정회귀직선을 구하는 방정식을 편미분하는 과정을 통해 도출해낼 수 있다
- 도 같은 방식으로 편미분하면 라는 식을 도출할 수 있고 여기서 는 각각 를 나타낸다.
- 쉽게 나타내면 으로 나타낼 수 있다
오차(error)와 잔차(residual)
-
많은 사람들이 혼동하여 사용하는 개념이다. 실제로 큰 차이는 없지만 다만 집단이 모집단이냐 표본이냐에 따라 다르게 사용한다.
-
회귀분석은 기본적으로 모집단 내에서의 변수 의 관계를 알기위해 사용한다. 즉 평균과 같이 모회귀선을 찾는 것을 목표로 한다.
-
하지만 늘 그렇듯 불가능 하기에 표본집단을 이용하여 추정하게 되는데 이때의 추정치가 위에서 구한 이 되는 것이다.
-
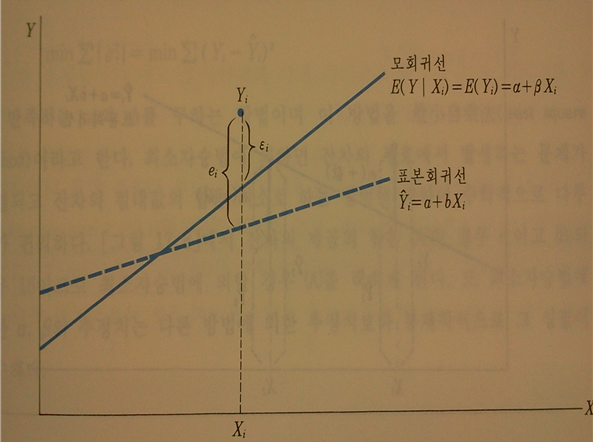
맨 위에서 나온 의 경우 모회귀선의 값()과 관측값() 사이의 관계를 나타내므로 오차라고 부르고 추정치인 와 관측값()사이의 차이를 잔차라고 부른며 로 표시한다.
-
쉽게말해 오차의 추정치를 잔차라고 부른다.
잔차제곱합(residual sum of squares; SSE)
- 이전에 구한 추정항들을 이용하여 SSE를 구한다.
- 위에 정규방정식을 이용하여 잔차가 가장 적을 경우의 추정항을 구하고 그 추정항들의 제곱합을 SSE를 이용하여 구한다.
- SSE은 작으면 작을수록 좋다
오차항의 분산
= MSE(평균제곱오차)
선형관계의 강도
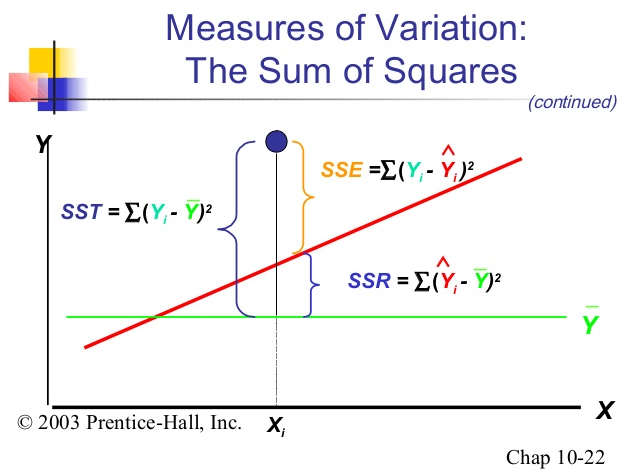
- SST(total sum of squares) : y값들이 나타내는 변동의 크기라고 말하고 총제곱합이라고 한다.
- SSR(regression sum of squares) : 회귀제곱합이라 하고 우리는 y값을 통해 회귀선을 예측하였으므로 이는 분석을 통해 설명이 가능한 수치라고 말할 수 있다
- SSE(error sum of squares) : 잔차제곱합이라고 이는 우리가 구한 예측값과 실제값의 차이인데 이것은 회귀식으로만으로는 설명불가능한 수치이다.
- SST = SSR + SSE
결정계수 ()
- 선형모형이 어느정도 적합한지를 나타내는 측도
- SSR이 크다는 것은 SSE가 작아진다는 뜻으로 설명불가능한 변동이 줄어드니 추정한 모형이 더 유의미하다는 뜻임
- 1에 가까울수록 회귀모형이 좋은 것임
모형의 타당성 검토
1. 선형성 : 의 평균은 0
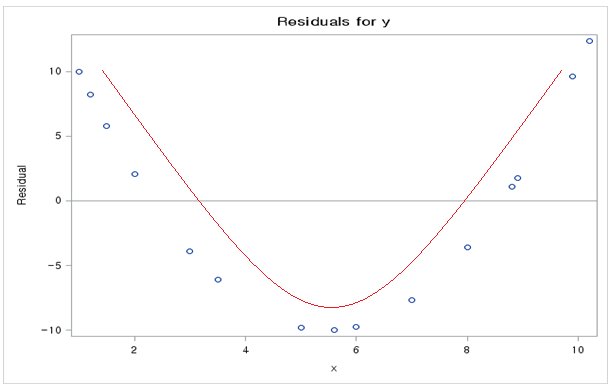
-
등분산성 : 의 분산은 으로 일정
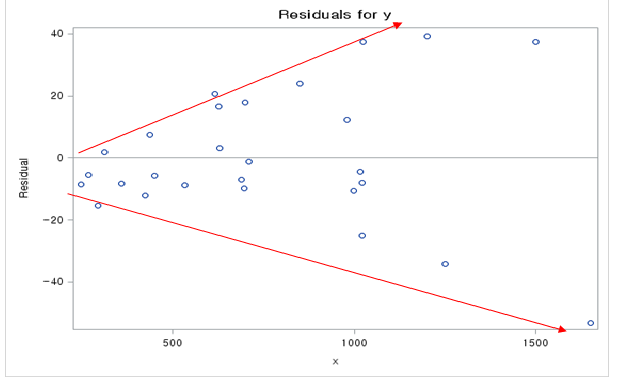
-
정규성 : 은 정규분포 ~을 따름
-
독립성 : 들은 서로 독립
