두 변수 자료의 요약

---

두 변수 자료

---

• 조사 대상으로부터 두 개 이상의 변수들을 동시에 관측하는 경우
• 주로 두 변수 사이의 연관성에 초점을 둔다
• ex) 아버지와 아들의 키, 학생의 국어, 영어, 수학 성적 등

두 변수 자료의 요약

---

두 범주형 변수의 요약 : 분할표

---

• 두 변수가 모두 범주형인 경우에 표를 이용하여 요약한다
• 2차원 도수분포표
  • 가로 : 한 변수에 대한 범주
  • 세로 : 다른 변수에 대한 범주
  • 각 칸 : 두 변수들에 해당하는 도수 혹은 상대도수를 기록
    
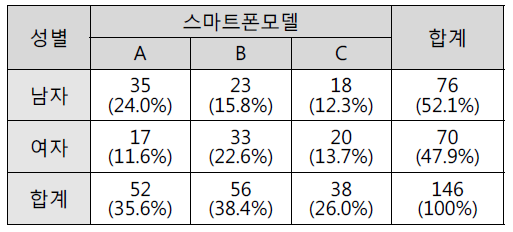
• 여기서 상대도수를 이용하면 각 자료가 차지하는 비율을 더 명확하게 파악할 수 있다

두 연속형 변수의 요약 : 산점도

---

• 두 변수가 연속형일 경우 그 관계를 파악할 수 있는 그림

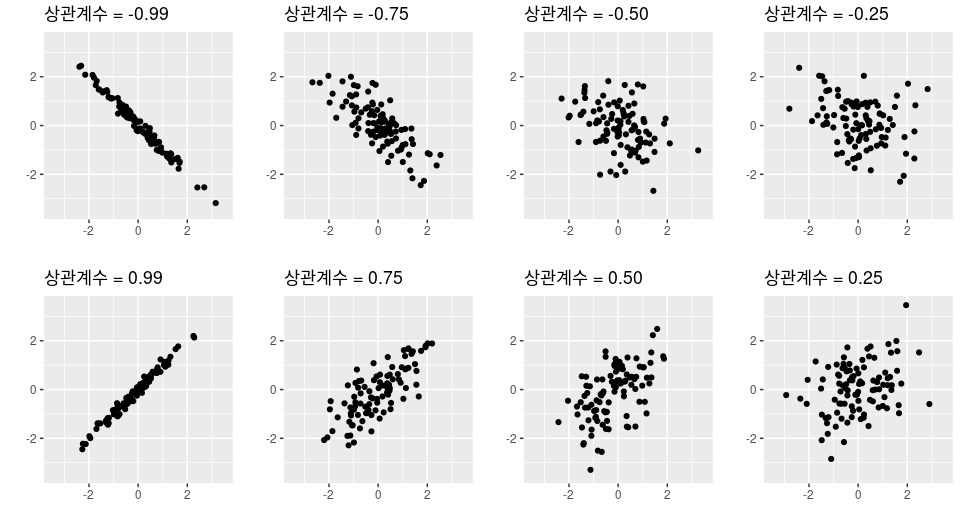
• 변수 x,y가 해당되는 위치에 점을 찍고 그 분포를 통해 해석함
• 따라서 두 변수의 연관성을 대략적으로만 파악할 수 있고 해석하는 사람에 따라 결과도 주관적일 수 있음

공분산

---

공분산은 나중에 나오지만 상관계수를 이해하기 위해서 필요하다고 생각함

• 공분산 : 공+분산으로 여러개(공)의 분산이라는 뜻이다
• 즉 이전에 하나의 변수만으로 구한 분산과 달리 두 변수를 이용하여 구한 것이 공분산이 되는 것이다
  

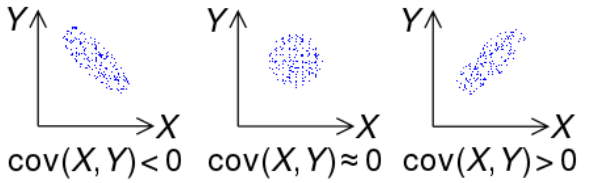
공분산을 왜 쓰는 것일까
이전에 분산을 사용할때 자료의 얼마나 퍼져있는지 분포를 확인하기 위해 사용했다. 만약 자료들이 평균에서 멀리 떨어져있으면 분산을 커질 것이고 자료들이 평균 주변에 분포하고 있다면 분산의 값은 작아진다.
똑같은 원리로 공분산도 적용될 수 있다.
$COV(X,Y)=\frac{ (x_{1}-\mu_{x})(y_{1}-\mu_{y})+ (x_{2}-\mu_{x})(y_{2}-\mu_{y})+ ...+ (x_{n}-\mu_{x})(y_{n}-\mu_{y}) }{n}$
먼저 공분산의 식을 살펴보면 각항에서 xn,yn이 둘다 평균보다 크거나 작으면 양수가 나올 것이고 둘중 하나만 크고 나머지 하나는 작다면 음수가 나올 것이다. 만약 즉 둘다 평균보다 크거나 작다라는 것은 그래프가 우상향 하는 것을 뜻한다(위그림의 3번째) 만약 둘중 하나만 크고 나머지가 작다는 것은 우하향 그래프라고 생각하면 된다(위그림의 1번째) 따라서 이렇게 일정한 패턴이 나타난다면 공분산은 절대값이 큰 양수 혹은 음수가 나온다. 그럼 2번째 그림처럼 0에 가까운 그림은 어떻게 나올까. 식을 보았을 때 각 항을 더하니 양수 음수가 계속 섞여서 더해진다면 절대값은 커지기보다 0에 가까워 질것이다. 즉 평균을 기준을 하였을 때 일정한 패턴없이 뒤죽박죽 섞여있다 즉 상관관계가 낮다라고 판단할 수 있는 것이다.

상관계수

---

• 두 연속형 변수 사이의 연관성을 객관적인 수치로 나타내는 방법
• 위의 공분산만으로는 각기 다른 항목들을 비교할 수 없다.
• 예를들어 키, 몸무게의 공분산을 비교해보면 키는 평균적으로 150이 넘겠지만 몸무게는 80정도밖에 안될 것이다. 이를 이용해 공분산을 구하게되면 당연히 두 값에서는 차이가 날 것이고 이를 위해 표준화해주는 것이 필요하다.

표본상관계수 Pearson correlation (r)

---

• 산점도의 점들이 얼마나 직선에 가까운지 나타내는 척도
• Pearson correlation (r)
• $r = \frac{공분산}{x표준편차\times y표준편차}$
• 성질
  1. $-1\leq r \leq 1$
  2. $r$의 절대값이 1에 가까울수록 선형관계가 강하고 0에 가까울수록 선형관계가 약함
  3. $r$의 부호는 방향을 나타냄 / $r\gt0$ 우상향 / $r\lt0$ 우하향
  4. $|r|=1$은 모든 값이 직선 위에 있다라는 것을 의미함

• 주의할 점 : "상관계수는 인과관계를 뜻하지 않는다"
• x가 y와 상관계수가 1에 가깝더라도 사실상 인과관계는 다른 잠재변수인 z와 있을 수도있다.
• 이러한 것들은 더 폭넓은 전문지식을 통해 해결해야함
  

스피어만 상관계수(Spearman's rank correlatoin(p)
피어슨 상관계수와 비슷한 개념이지만 이는 순위형 자료를 이용하여 구함 이산형자료도 순위를 구할 수 있다면 사용할 수 있음
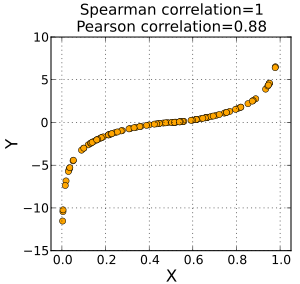
피어슨 상관계수와 다른점은 피어슨 상관계수는 완전한 선형관계일때 $|r|=1$의 값을 가지지만 스피어만 상관계수는 순위를 이용하기에 완전한 선형이 아니거나 혹은 비선형이어도 1의 값을 가질 수 있다. 예를들어 1,2,3,999의 값이 있을 경우 비선형 그래프 이겠지만 순위를 매기게되면 1,2,3,4가 되므로 p의 값은 1에 가깝게 나올 수 있다. 반면 피어슨 상관계수를 이용하면 1과는 거리가 먼 값이 나올것이다.

위 그림처럼 피어슨과 달리 스피어만 상관계수는 비선형이어도 연관성이 있으면 1의 값을 가진다

심슨의 역설

---

• 여러 그룹의 자료를 합했을 때 각 그룹의 결과와 반대가 되는 현상
• 전체의 평균은 A가 높지만 각각의 항목의 평균은 모두 B가 높은 현상
  
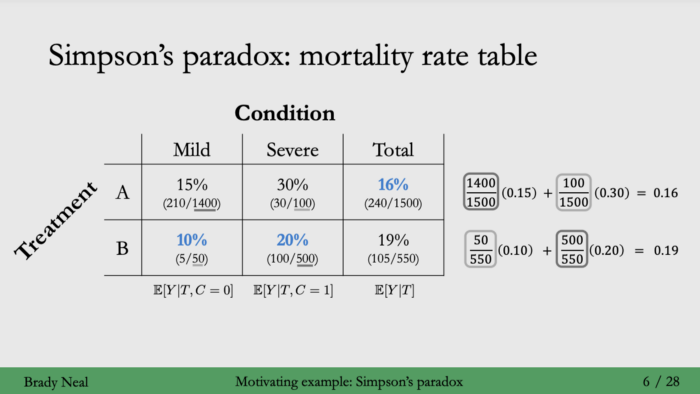
• 위그림을 보면 전체의 사망률은 B가 높지만 각각의 항목에 대해 사망률은 A가 더 높음을 알 수 있다.
• 이렇게 된 이유는 사망률이 더 적은 Mild항목에서 A를 맞은 사람들이 많았고 사망률이 더 높은 Severe에서 B를 맞은 사람이 많았기에 전체적으로 B의 사망률이 더 높아 보이는 것이다.
• 즉 심슨의 역설이라는 현상이 생기는 이유는 Confunding Variable 즉 교란변수를 고려하지 않았기 때문이다.
• 뿐만아니라 그 교란변수의 불균형적인 할당이 통계치에 큰 영향을 주는 경우에 발생한다.