통계적 추론(표본의 크기가 클 때)

통계적 추론

---

• 표본의 정보를 통해 모집단의 특성을 추론

추정량, 추정치

---

1. 추정량 : 추정치를 구하기 위해 사용되는 추정 방법이나 도구

• ex) 모평균의 추정량은 표본평균이고 모분산의 추정량은 표본분산이다

2. 추정치 : 추정량의 구체적인 수치값

점추청

---

• 모수를 하나의 값으로 추정
• 단점 : 점을 하나만 가지고 추정하기에 추정치가 다르게 나올 가능성이 높음

  표준오차
  추정치가 항상 정확할수 없기에 추정치가 모수에 얼마나 가까운지의 정확도를 측정하기위한 도구
  $S.E.(X) = \frac{\sigma}{\sqrt{n}}$
  자료의 수가 클수록 표준오차가 작아져서 정확한 추정이 가능
  표준편차와 헷갈리면 안됨 : 표준편차는 모집단 내에서의 퍼진정도를 나타내고 표준오차는 표본통계량과 모수간의 오류의 가능성 정도를 나타낸 것임

구간추정

---

• 점하나만으로 추정하는 점추정의 정확성 문제로 인해 이를 극복하고자 일정한 구간을 정해놓고 추정하는 방식
• 구간의 길이가 길수록 추정의 정확성은 높아지지만 구간의 길이가 짧을수록 추정의 가치가 높아진다

신뢰구간, 신뢰수준

---

• 신뢰구간 : 모수를 추정하는데 이용되는 구간 $(L,U)$
• 신뢰수준 : 신뢰구간이 모수를 포함할 확률

신뢰수준이 같다면 길이가 더 짧은 구간이 더 좋다. 위에서도 나왔지만 추정의 정확성이 같다라고 가정되면 길이가 짧은게 더 좋은것이 논리적으로 옳다.

• 신뢰구간 구하기
  "$\mu$에 대한 $100(1-a)\%$ 신뢰구간"
  $X$~$N(\mu,\frac{\sigma^2}{n})$를 표준화하여 $\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$~$N(0,1)$로하면
  $P(-z_{a/2}\leq\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq z_{a/2}) = 1-a$
  ex) 95%신뢰수준에서 신뢰구간을 구하면 $z_{0.025} = 1.96$
  $-1.96\leq\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\leq 1.96$
  $\overline{X}-z_{a/2}\frac{\sigma}{\sqrt n} \leq \mu \leq \overline{X}+z_{a/2}\frac{\sigma}{\sqrt n}$ 를 적용시켜
  $\overline{X}-1.96\frac{\sigma}{\sqrt n} \leq \mu \leq \overline{X}+1.96\frac{\sigma}{\sqrt n}$ 혹은 $\overline{X}\pm1.96\frac{\sigma}{\sqrt n}$ 으로 나타냄

  신뢰구간이 짧아질 조건
  신뢰도가 낮을수록, 표본의 크기 n이 클수록, 표준편차가 작을수록 짧아진다.

  신뢰구간의 의미

  • ex. 95%신뢰구간 표본을 여러번 추출하였을때 이 구간 중 모평균을 포함하는 표본의 비율이 95%에 가까움
  • $\overline{X}\pm z_{a/2}\frac{s}{\sqrt n}$와 $\overline{x}\pm z_{a/2}\frac{s}{\sqrt n}$는 큰 차이가 있다.
    먼저 확률변수 X의 경우 각 확률변수는 정해져 있지 않다. 따라서 표본에따라 그 표본에 맞게 신뢰구간이 계속바뀌고 우리는 이 구간에 $\mu$가 있을확률이 $1-a$라고 할 수있다.
    표본평균 x의 경우 이미 정해져있는 값으로 이 구간에 $\mu$가 포함되거나 포함되지 않거나 둘 중 하나이다. 따라서 이 구간에 $\mu$가 있을 확률이 $1-a$라는 것은 옳지 않다.

  일반적으로 모집단은 분포나 표준편차가 알려져있지않다. 그럼 신뢰구간을 구할때 $\sigma$는 어떻게 하는가.
  n이 충분히 클때 : 표본의 표준편차 $s$는 $\sigma$의 값과 가까울 것이기에 대체하여 신뢰구간을 구한다. 즉, $\overline{X}\pm z_{a/2}\frac{s}{\sqrt n}$
  로 하면된다.

표본크기 결정

---

• 표본의 크기를 뽑을때 많이 뽑을수록 신뢰도가 올라가니 좋겠지만 그렇다고해서 무턱대고 뽑으면 시간과 비용이 많이 들게된다. 따라서 표본을 뽑을때 너무 많지도 적지도 않은 적당한 크기의 표본을 뽑는 것이 중요하다.

먼저 허용오차라는 개념에 대해서 알아야한다. 통계는 항상 100% 정확할수없고 어느정도의 오차가 생기기마련이다. 하지만 우리가 이정도 오차까지의 허용은 괜찮다라고 말할수 있는 최대한의 범위가 허용오차인 것이다. 신뢰구간 또한 점추정에서의 허용오차라고 볼수도 있다.

• $P(|\overline{X}-\mu| \leq d) \geq 1-a$ : 추정오차가 d이하일 확률이 최소 $1-a$를 만족하는 최소 표본의 크기이고 이를 $P(\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\geq z_{a/2}) \geq 1-a$와 연립하면 $z_{a/2}\frac{\sigma}{\sqrt n} \leq d$라는 값이 나오고 따라서 $n \geq (z_{a/2}\frac{\sigma}{d})^2$이라는 값을 도출할 수 있다.
• 만약 모집단이 정규분포를 따르지 않더라도 $n \geq 30$이라면 중심극한정리를 이용해 사용할 수 있고 이 경우 $\sigma$대신 $s$를 사용할 수도 있다.

굉장히 모순적인 말이지만 표본크기는 결국 많으면 많을수록 좋기에 허용오차와 관계없이 가능한 많은 표본을 뽑는 것이 중요하다.

모평균에 대한 검정

---

가설검정

---

• 표본이 제공하는 자료를 토대로 가설을 받아드릴지 기각할지를 검정하는 방법이다.

• 대립가설$(H_1)$ :
  귀무가설의 반대로 입증되기를 기다리는 가설
  귀무가설이 기각되면 대립가설이 선택된다.

• 귀무가설($H_0)$ :
  실제로 연구에서 검증하여야하는 가설
  기본적으로 참으로 추정하며 이를 반박하기위해서는 근거가 필요함
  귀무가설이 참이라면 귀무가설을 채택, 그렇지 않다면 기각

• 검정결과의 표현 :
  귀무가설을 채택한경우 "귀무가설을 기각하지 못함"
  대립가설을 채택한경우 "귀무가설을 기각"
  모든 기준이 귀무가설임을 알 수 있음

• 검정통계량 : 가설검정에 이용되는 통계량

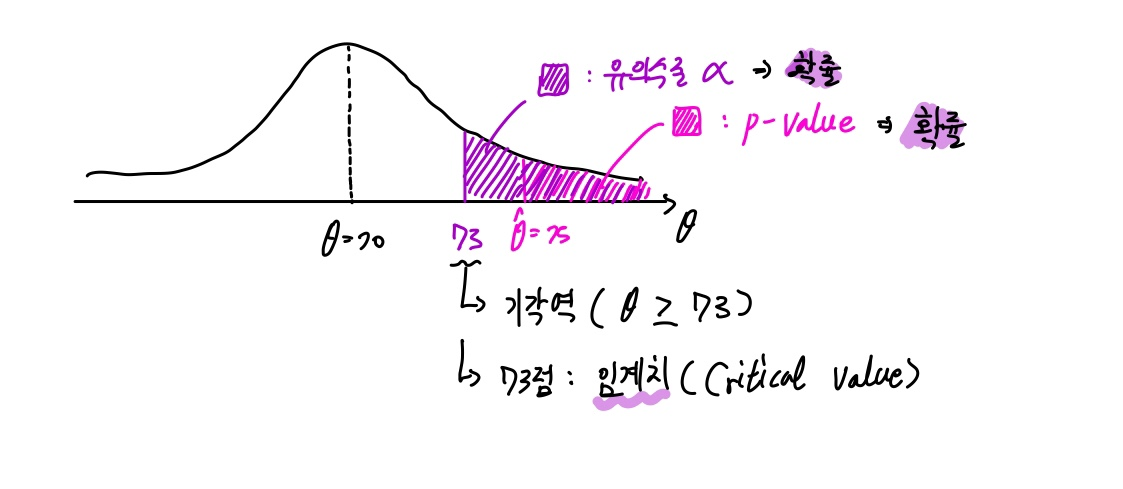
• 기각역 : 귀무가설을 기각하게되는 관측값의 영역
  ex) 5kg이상 빼지못하면 다이어트 실패이고 귀무가설이 80 kg인 사람의 다이어트 실패라면 5kg이상빼면 귀무가설이 기각되기때문에 기각역은 $\overline X \leq 75$가 된다.

오류의 종류

---

• 제 1종 오류($\alpha$) : 귀무가설이 참일때, 귀무가설을 기각

  • 오류의 가능성 : $H_0$가 맞지만 $\alpha = P(\overline X \leq C)$이므로 $H_0$를 기각하게 되는 경우

• 제 2종 오류($\beta$) : 대립가설이 참일때, 귀무가설을 기각하지못함

  • 오류의 가능성 : $H_1$가 맞지만 $\alpha = P(\overline X \gt C)$이므로 $H_0$를 채택하게되는 경우

• 1종오류를 줄이려면 $C$를 작게해야지만 2종오류를 줄이려면 $C$를 크게해야함 따라서 적절하게 조정하여 기각역을 설정해야함
  

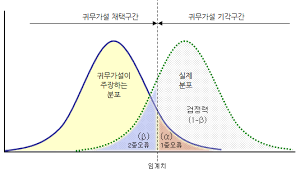
일반적으로 1종오류가 2종오류보다 심각함 귀무가설을 기각하지 못하는 2종오류의 경우에는 기존에 하던 방식을 그대로 진행하면 된다. 다만 이미 새로운 대안이 나왔음에도 그것을 채택하지 못하는 기회를 날리는 격이다. 하지만 1종오류의 경우 새로운 대안이 옳은 대안이 아님에도 불구하고 기존의 방식을 바꾸는 격이되기에 매우 위험한 오류라고 본다. 따라서 2종오류보다 1종오류에 더 초점을 맞추어야한다.

유의수준($a$)

---

• 1종 오류가 일어날 확률의 최대허용치
• 위에서 1종오류가 2종오류보다 더 조심해야했기에 1종오류가 기준이되고 일반적으로 유의수준은 0.01(1%), 0.05(5%)를 주로 사용한다.
• 5% 유의수준이라는 말을 쉽게 풀면, 귀무가설이 참임에도 불구하고 관측값이 귀무가설을 기각하라고 나올확률이 5%미만이라는 것이다. 즉 1종오류가 일어날 확률이 최대 5%라는 뜻
• 더 쉽게 풀면 귀무가설이 참이지만 우연히 귀무가설이 거짓이라는 결론을 낼 확률이 5% 미만이라는 뜻이다.

z-검정

---

• z-분포를 이용하여 가설을 검정하는 방볍
• 여기서 z-분포란 표준정규분포를 뜻함
  • 모집단의 평균과 표준편차를 알고
  • 표본의 크기가 크거나 모집단이 정규분포를 따라야함
  • 두 집단을 비교할경우 분산이 같아야함
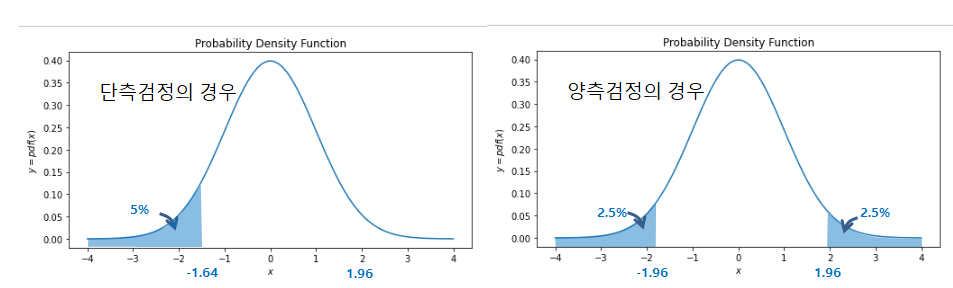
• z-검정은 단측검정과 양측검정 두가지로 이루어져있는데 말 그대로 우리가 구하고자하는 값이 같지 않다라는 전제라면 양측검정을 사용하고 더 작다 혹은 더 크다라는 경우 단측검정을 사용한다.
  

유의확률(P-value)

---

• 매우 헷갈리는 개념인 유의수준과 유의확률을 비교하여 설명하겠음
• 일단 유의수준의 경우는 실험전 실험자가 임의로 지정해놓는 값(기각역)이라고 생각하면된다. 예를 들어 나는 5%의 유의수준까지 감안해서 실험을 하겠다라는 전제를 두고 실험을 한다라는 소리다
• 이에 반에 유의확률은 실제 실험을 통해서 나오는 값이고 위에 예시를 이어 6%의 유의확률이 나왔다고 가정하면 설정한 기각역인 5%를 넘었기에 귀무가설을 기각하지 못한다. 만약 3,4%가 나와서 유의수준보다 적다면 귀무가설을 기각할 수 있다.
• 쉽게말해 유의수준은 실험전 실험자가 수용할수 있는 기준이고 유의확률은 그 기준에 부합한지 아닌지를 판단하는 실험값이라고 생각하면된다.
• z검정에서는 z검정에서 나온 좌푯값의 확률을 유의확률이라고 부를 수 있겠다.