Machine Learning
데이터 분석에서 벡터란?
벡터의 정의
- 벡터 공간의 원소
- 여러 개의 숫자 모음 ( list of numbers)
- 점 ex) a( 1,2) , b(1,2,3)
벡터 공간
- 축 (axis) : x,y,z축
- 차원(dimension) : 벡터의 원소의 개수
- a(1,2,3)의 원소의 개수가 3개이므로 “3차원”에 해당
- 원소(elemet) : 벡터
데이터를 벡터로 표현한다고 할 때,
기준(칼럼,도메인)을 정할 시 고려해야 하는 사항
- 분석하는 사람이 필요에 따라 선택한다. → 정답이 없으며, 분석가가 논리적으로 선택 이유를 설명할 수 있으면 됌
벡터 간 거리
- 데이터 사이의 유사성 측정
- Ex) N차원의 벡터 = (x1,x2,,,,,,,xn) , (y1,y2,,,,,,Yn)이 있을 경우
- Manhattan Distance ( L1 ) : ㅣN차원 벡터의 원소값의 차 l 의 모든 합 → 밑변,높이 → Data값을 좀 더 자세히 확인 할 때
- Euclidean Distance ( L2 ) : (N차원 벡터의 원소값의 차)의 제곱의 루트 → 대각선 → Data값을 뭉뚱그려서 확인 할 때
Feature Space
- Raw data ————————————> Feature vector
- 주어진 Raw data중 필요한 특징을 추출(선별)하여 vector로 표현한 것을
feature vector라고 한다.
- feature selection (선별)
- feature extraction (추출)
- 해당 추출과정을 feature engineering이라고 한다.
- 주어진 Raw data중 필요한 특징을 추출(선별)하여 vector로 표현한 것을
- Embedding (REE)
Machine Learning
Machine Learning의 의미
- 사람의 학습방법과 동일하게 데이터를 통해 패턴을 찾아내는 방법
컴퓨터가 주어진 입력값(x)과 찾고자 하는 값(y) 사이의 관계를 모델링 하는 방법경험(E)를 통해 주어진 일(T)에 대해 퍼포먼스(P)로 측정한 값이 향상되는 프로그램- 컴퓨터에게 데이터를 바라보는 방법(모델)과 예시(데이터)를 주고 판단을 내리는 기준을 찾는 방법
- 위의 방법 모두 Feature Engineering의 과정
Kind of Machine Learning
데이터의 존재 유무에 따라 지도학습과 비지도 학습으로 구분
Supervised learning —> 지도학습 (값이 존재)
→ 입력 데이터(X)와 그에 해당하는 정답(y)가 함께 학습에 사용되는 방법론
- Ex) 해설지를 풀고 정답을 맞추어 가는 경우
Regression(회귀): 종속변수가 연속형데이터
→ 주어진 데이터(X)와 관련이 있다고 생각하는 값(y) 사이의 *관계*를 찾는 방법
- 연속형 데이터 - 매출데이터, 온도, 시간등
- 자연수 0과 1사이에는 무수히 많은 실수가 존재하고 그 무한한 값의 범위를 갖는 데이터를 연속형 데이터라 한다.
Classification(분류): 종속변수가 범주형 데이터
→ 주어진 데이터(X)를 몇 가지 종류로 나누는 방법
- 범주형 데이터 - 성별, 신용등급, 브랜드, 기차역등
- 남성 혹은 여성 구분처럼 이진형 구분(0 혹은 1), 데이터가 특정 범위내에 모두 속한 데이터의 경우 범주형 데이터 혹은 카테고리 데이터라고 한다.
Unsupervised learning —> 비지도학습 (값이 존재하지 않음)
→ 입력 데이터(X)만 학습에 사용되는 방법론 ( 정답 y가 주어져 있지 않은 경우 )
- Ex) 자기주도학습! 답안지 안보고 푸는 경우
Clustering(군집화) : 종속변수가 범주형 데이터
주어진 데이터(X)를 몇 가지 그룹으로 나누는 방법- 정답이 없는 데이터를 모델에 따라 비슷한 샘플끼리 묶어주는 머신러닝 알고리즘
- 데이터에 숨겨진 특징이나 구조를 발견하여 같은 특징에 따라 구분
Dimensionality Reduction( 차원 감소 기법)
주어진 데이터(X)의 중요한 정보들을 뽑아내는 방법- 요약된 수치들로 표현 가능 → 차원축소 ( 축소하는 정도가 정해져 있지 않음)
Association rule analysis(연관규칙분석) : 종속변수가 스코어 혹은 샘플
- 보통 추천시스템이라 부르며 매출 및 유저의 구매기록에 기반한 규칙을 찾는 알고리즘
- 아이템 혹은 유저를 기준으로 비슷한 아이템 및 유저를 찾아 비슷한 데이터를 찾음.
Reinforcement Learning (강화학습)
→ 행동의 대상과 환경사이의 상호작용을 통해서 목표를 최대화하는 학습 방법론 (ex) 주식)
- Real-time decisions
- 주어진 환경에 대해서 reaction을 하면서, 최적화가 필요한 방법론
- Game AI
- AlphaGo,DeepBlue,AlphaStar… etc
Semi-supervised learning(준지도학습) : 비지도학습 + 지도학습
- 지도학습을 사용하려면 레이블이 있어야 하지만 이를 비지도 학습으로 해결
- 종속변수에 레이블이 있는 데이터와 없는 데이터를 같이 사용
- 군집화와 지도학습을 순차적으로 적용하는 방법
-
적용 순서가 정해져 있지는 않지만, 일반적으로 군집화 → 지도학습
객관적 평가 불가능
-
Scikit-Learn
Scikit-Learn : 파이썬 오픈소스 라이브러리 중 머신러닝을 구현하는데 특화된 라이브러리Sklearn: 구현방식
**# 1. 사용할 모델을 불러오기**
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
**# 2. 모델 객체 선언하기**
model = RandomForestClassifier()
**# 3. training data로 학습진행하기**
model.fit(X_train,y_train)
**# 4. test data로 inference 진행하기**
pred = model.predict(X_test)
**# 5. Evaluation metric으로 평가 진행하기**
print( "Accuracy : %.4f" % accuracy_score(y_test,pred) )
Ex) >> Accuracy : 0.8976필수개념
Data Split
→ 학습에 사용할 데이터와 평가를 할 때 사용할 데이터를 나누는 방법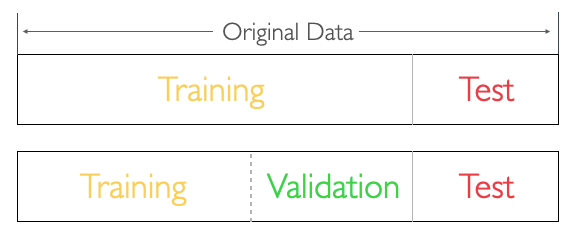
- Data Split은 train-test split을 의미한다.
- training data는 학습에 사용하고 test data는 평가에 사용한다
- 8년치 공부하고(오답정리) , 2년치는 시험 직전 날 풀기
- train - test split
- 6년치를 공부하고(오답정리), 그 때마다 2년치를 풀어보고 점수 체크 후, 시험 직전날 2년치 풀기
- train - validation(검증) - test split
- 안 풀어본 문제에 대한 예측을 잘 하기 위함 ( Prediction for Unseen data)
- 지속적인 검증을 통해 학습이 잘 수행되고 있는지 확인 가능
- 예측 성능을 올리는 것이 중요.
- train - validation(검증) - test split
- 8년치 공부하고(오답정리) , 2년치는 시험 직전 날 풀기
Training
→ 머신러닝 모델이 데이터의 패턴을 파악하는 과정
- 데이터를 확인 한 후, 정해진 기준에 따라 정보를 학습
- 학습된 정보를 기준으로 판단
- 판단한 정보를 바탕으로 성능을 평가
- 평가한 성능이 점차 향상되는 것이 목표
→ 주어진 데이터로부터 정보를 얻고, 성능이 향상 될 수 있는 방향으로
**Parameter(정보)를 업데이트**해 나가는 과정을 Training(학습)이라 한다.
Inference
→ 학습된 머신러닝 모델에 test data를 넣어서 결과를 내는 과정
-
학습된 모델과 test data가 있어야 가능
-
inference에서는 학습이 발생하지 않음 ( 오답정리 x)
-
정해진 모델에 대한 평가만 이루어진다
-
객관성을 유지하기 위해 train data가 아닌
test data를 사용→ 궁극적인 학습 목표는
inference(추론)의 성능이 높아지길 기대하는 것
→ prediction for Unseen data
Feature Engineering
→ Input vector를 머신러닝 모델에 사용할 feature vector로 바꾸는 작업
Raw data → ( feature engineering ) → Feature Vector
- feature engineering을 통해 input data는 p를 높일 수 있는
feature vector(수치정보)로 변환- feature vector를 만드는 방법을
feature extraction algorithm- PCA,Component Analysis,AutoEncoder
- feature vector를 만드는 방법을
- Deep Learning 영역에서는
Embedding방식을 사용 → 추후 설명
Loss Function
→ 모델의 inference 결과(예측값)와 실제 값(y) 사이의 틀린 정도를 계산하는 함수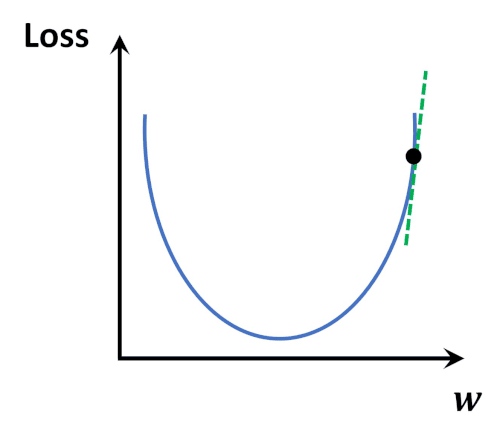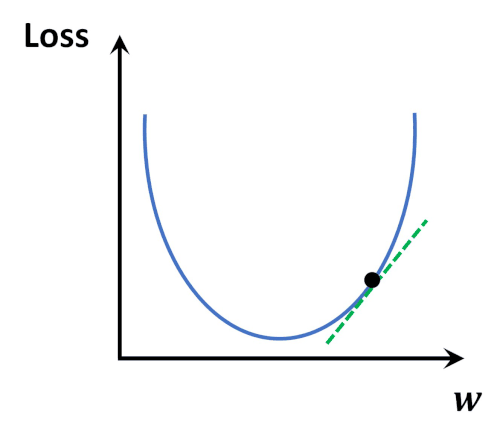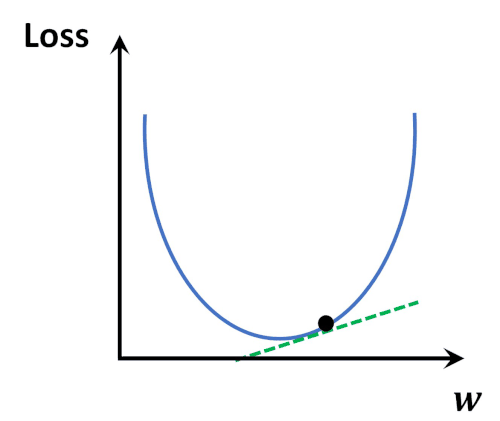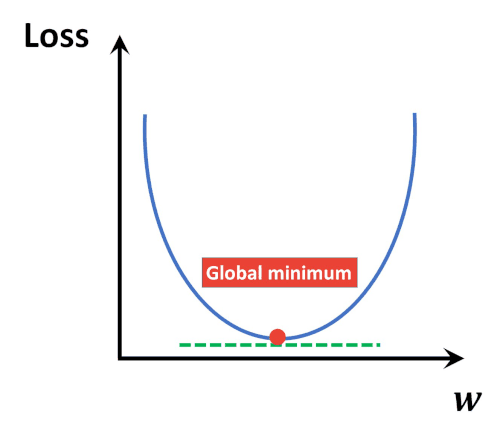
https://datahacker.rs/003-pytorch-how-to-implement-linear-regression-in-pytorch/)]
- (predicted value)와 (target value) 사이의 차이를 계산해주는 함수.
- - = Loss Function
- 덜 틀릴 수록 학습이 잘된 모델
Loss function의 결과에 영향을 주는 변수는 무엇?- Parameter( weights)
loss function의 계산 결과가 가장 작아질 수 있는 parameter를 찾는 것이 학습 목표
Loss Function Optimization
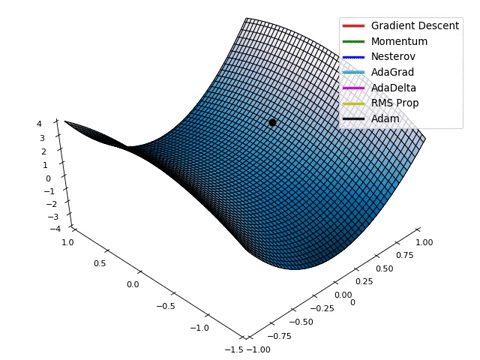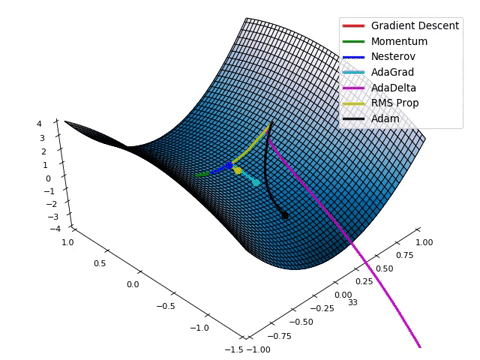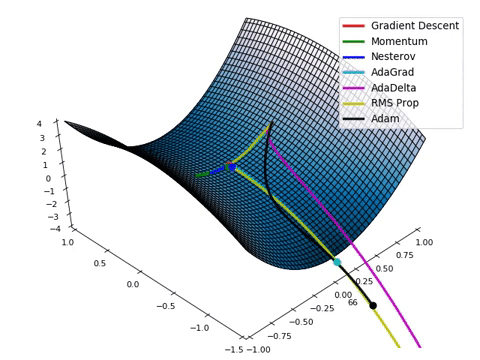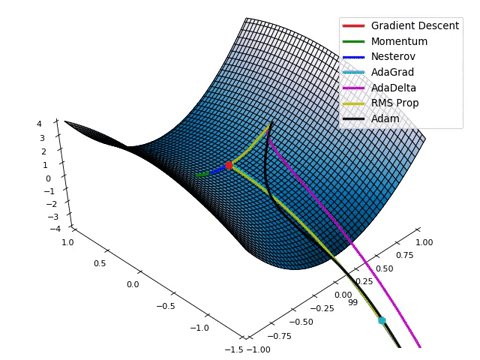
- 위와 같은 Loss space에서는 수학적으로 미분을 통해
극소점(parameter)을 찾는 점이 어려움. - Loss function이 최적값을 가질 수 있는 파라미터를 찾기 위해서는
파라미터를 적절하게 업데이트해주어야 한다- 성능이 향상되는 방향으로 파라미터를 업데이트 해주는 것이 중요. ( = loss가 줄어드는 방향 )
→ 현실적으로 최적의 파라미터를 찾기 위해 Gradient Desent Algorithm이 제일 많이 사용
Gradient Desent Algorithm
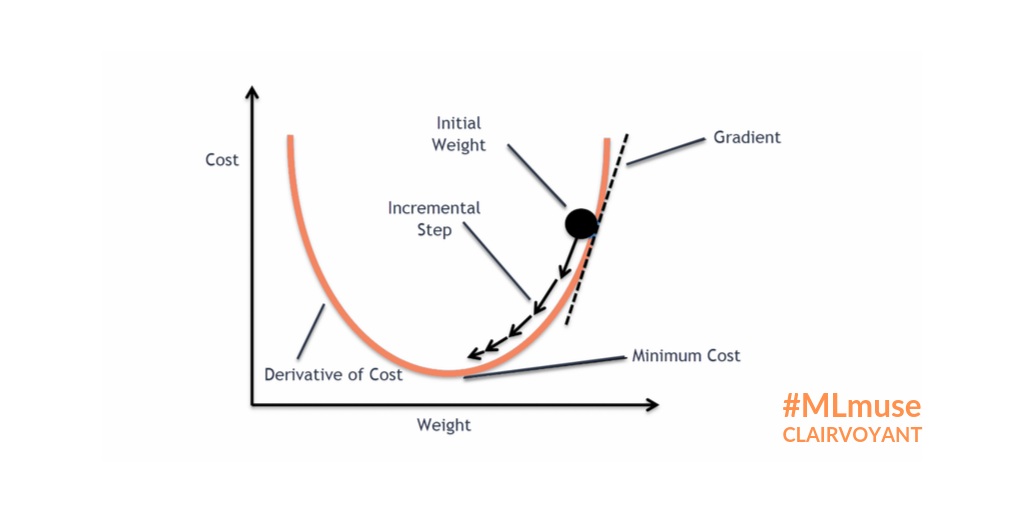
- 산맥에서 임의의 포인트에 떨어졌을 때, 현재 위치에서 가장 가파른 방향으로 한 발자국씩 내려가는 방법으로
최선을 다해 밑 바닥으로 내려 갈 수 있는 방법
- 대부분의 머신러닝 모델에 적용되어 있는 최적화 방식
- 파라미터가 점차 loss function에서 최소값을 가질 수 있게 파라미터를 업데이트 해준다.
- 단, 무조건 global minimum(최솟값)을 찾는 것은 아니고, local minimum(극소값)을 찾을 수도 있다.
- but 극소값은 무조건 찾는다.
Evaluation Metric
→ 머신러닝 모델을 평가하는 기준
- 머신러닝 모델의 성능을 평가하는 방버은 어떤 task(T)냐에 따라 다름
Metric for Classification
- →
: 맞은 개수의 비율 - → : 예측 모델이 positive로 예측한 것중에 실제로 맞은 비율.
- →
: 실제 positive중에서 예측 모델이 맞은 비율. - →
: precision과 recall의 조화평균. (둘 다 좋아야 좋게 나오는
평가 지표.)
Metric for Regression
- MSE ( Mean Squared Error)
→ 예측값과 실제값 사이의 차이를 제곱한 뒤 평균 낸 값
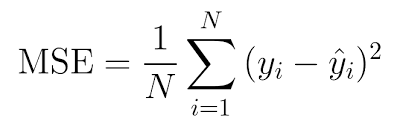
- score
→ 실제 값의 분산 대비, 예측 모델이 얼마나 더 실제 값을 잘 맞췄는지의 비율을 계산
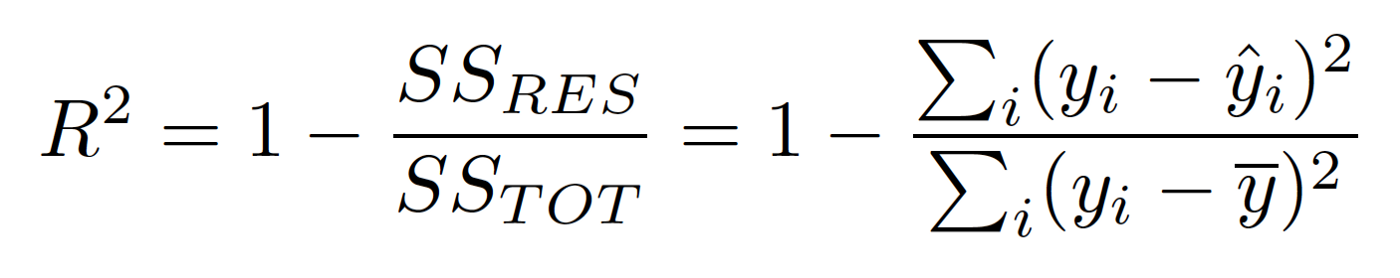
Metric for Clustering
- Silhouette Score
→ 어떠한 값을 기준으로 가까이 있고 멀리있는지를 측정한 지표 (best = 1, worst = -1)
Regression(회귀)
→ 회귀란, 주어진 input data와 관심 있는 target value 사이의 관계를 모델링하는 것을 의미- Input data는 일반적으로 벡터(차원,테이블,행렬) ( Feature vector)
- target value는 일반적으로 실수 (Real value)
- Feature vector로 target value를 예측하는 것을 목표 !
이를 위해서는 관계식이 필요한데, 이 관계식을 모델링하는 것이 회귀분석의 목표
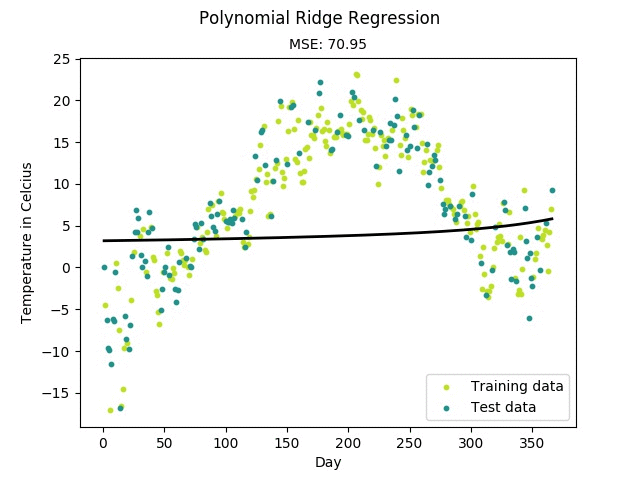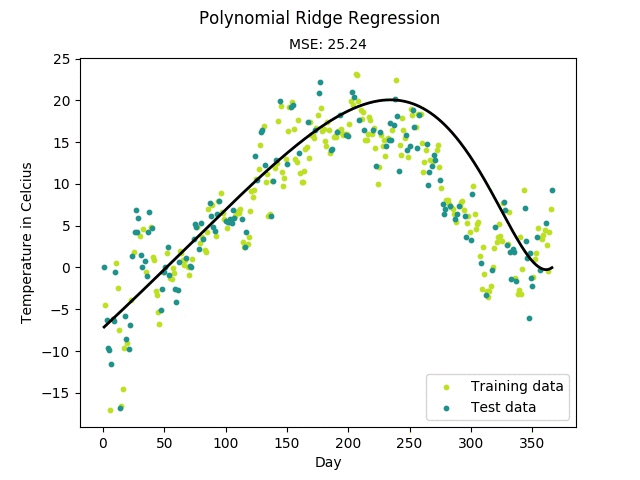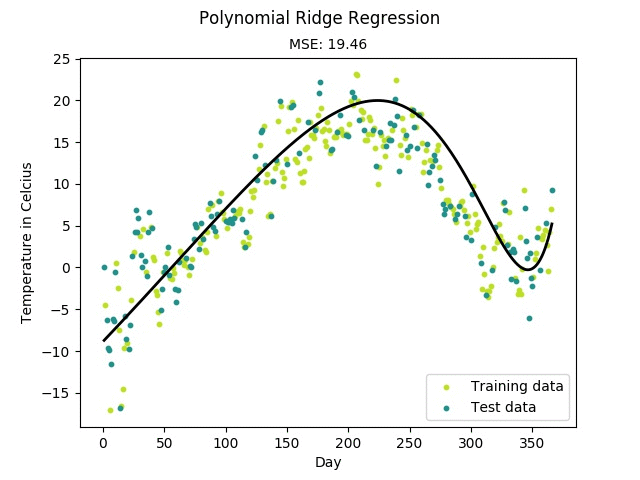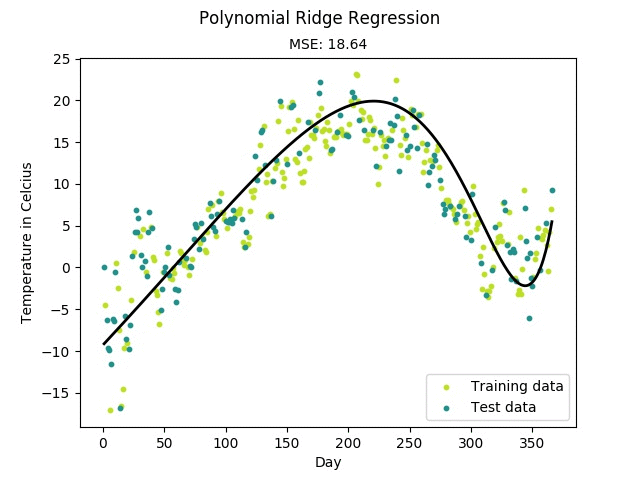
- 머신러닝 모델이 위와 같은 관계식을 찾게 되면, 해당 관계식에 test data를 inference한 결과가 예측값()이 됀다.
- 분류와 다르게 inference한 결과값 자체가 예측값이 됀다.
- 지도학습이기에, 주어진 target value를 찾는 방향으로 학습이 진행됀다.
회귀 분석의 종류
- 단순회귀 : simple regression
- 독립변수 1개, 종속변수 1개, 1차원 수식
- 다중회귀 : multiple regression
- 독립변수 2개 이상, 종속변수 1개, 1차원 수식
- 다항회귀 : polynomial regression
- 독립변수 1개 이상, 종속변수 1개, 2차원 이상의 수식
Summary-table
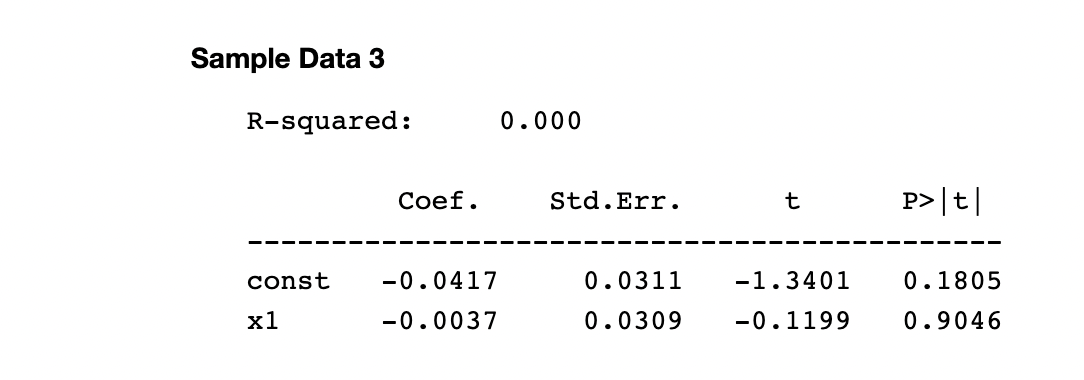
- R-squared
- 모델의 분산 설명력 의미
- 0 ~ 1 사이의 값을 가지며 1과 가까울수록 모델의 정확도가 올라감
- coef.
- 회귀계수
- 너무 0과 가까우면 모델에 영향을 거의 안 주게 되므로 계산량만 증가시킴
- std.err.
- 표준 에러
- 회귀모델에서 평균에 대한 추세선의 데이터 퍼짐 정도를 나타냄
- 높을수록 추세선의 신뢰도가 떨어짐
- 그렇다고 낮은게 항상 좋은것은 아님 > 회귀계수가 0과 가까우면 낮게 나옴
- t
- t-test
- 회귀계수가 우연인지 확인하는 지표
- 0과 가까울수록 우연일 확률이 높음
- P>|t|
- p-value
- t-test를 0 ~ 1 사이의 수치로 변환 한것
- 대체로 0.05 이하의 수치를 가지면 해당 feature는 유의한것으로 판단
- coef.
Regression Model
Linear Regression
→ y=Wx+b로 표시되는 선형식으로 X와 y사이의 관계를 찾는 모델
- 특정 값을 찾는 모델
- 해당 과정에서 에러(선형식 위(on)가 아닌 above/below에 위치)가 발생하는데 이를 줄여가는 과정 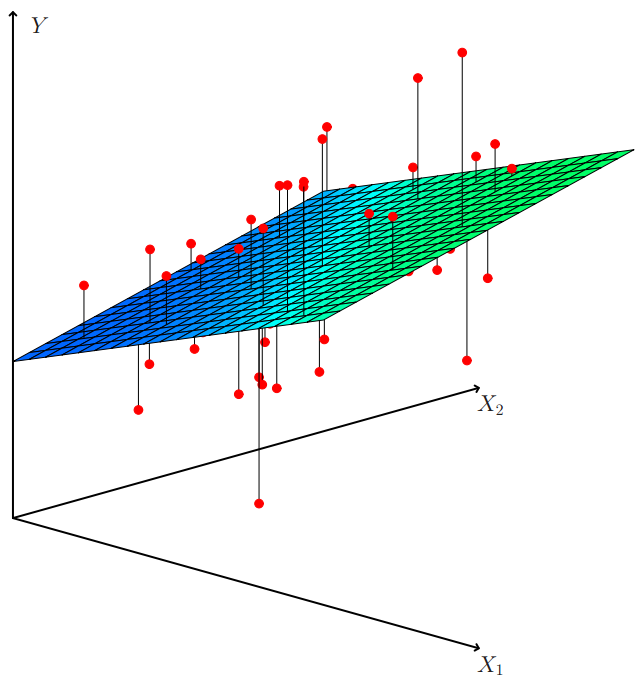
(https://enook.jbnu.ac.kr/contents/19/#!/p/28)
- X1,X2는 데이터 2차원 feature , Y는 target value
- Red point : (x1,x2,y)
어떤 선(면)을 찾는데 각 데이터(taget value) 거리의 차이가 최소가 되는 지점을 찾는 것.- 기본적으로 target value을 예측하는 것을 목표로 함
- target value를 찾기 위해서는 training data의 패턴을 찾아야함
- 회귀에서 가장 많이 사용하는
Loss function
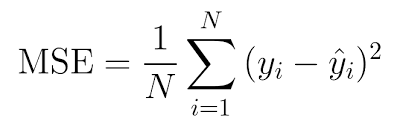
Data가 늘어남에 따라 Error도 증가. ( data가 많아지면 학습이 잘 되어야하는데 그렇지 않다..)
- 위의해결방안으로 평균으로 만들어준다.Why? 제곱의 합을 할까?-1, +1 값이 나올 시 수치가 더해져서 상쇄(0)되므로!!
- 모델 예측값()이 실제값()에 점점 가까워지게 학습 됀다. ⇒ 전체적으로 Loss의 평균이 작아지는 방향으로 학습이 진행
- 만약 차이가 큰
Outlier같은 데이터가 있다면Loss가 크게 나오므로미리 제거를 해주거나 보정을 해줄 필요가 있다 ⇒학습에 방해가 되기 때문에
- Linear Regression의 장단점
- 통계적으로
설명 가능한 이론 多(설명 도구가 많다.) interpretability
→ 수식 자체가 선형식이기에, 직접 계산을 해서 예측값이 왜 나오는지 설명이 가능
- 특정 수치값을 예측하는 건 좋지만, 특정 카테고리를 예측하는 것은 부적합
- Linear model 자체가 가지는 simplicity 때문에 general한 모델이 나오는 편
→ 오히려 복잡한 모델들 보다 예측력이 더 뛰어남
Linear regression도 역시 parameter W와b를 찾는 문제가 되고, 적절한 parameter를 찾았을 때 데이터를 잘 파악하는 선형식을 찾을 수 있게 됀다.
Lasso & Ridge
Lasso & Ridge : Linear Regression 모델이 고차원 공간에 overfitting이 쉽게 되는 문제를 해결- What is 고차원 overfitting?
- 변수가 많아지는 고차원 공간에서는 feature에 끌려다녀서 제대로된 학습이 불가
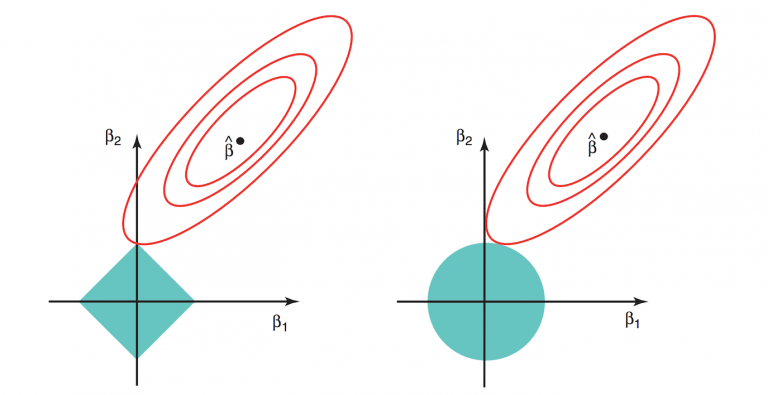
(http://freesearch.pe.kr/archives/4473)
- : Otimal coeff → otimla value (best)
- 의 best case
- 값에 따라서 제약조건 범위(마름모,원)가 변경
Lasso
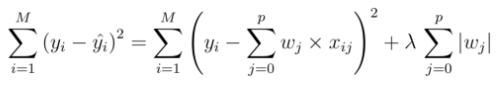
- x
- weight의 L1 term을 Loss function에 더해줌 (는 hyper-parameter)
- Loss가 무조건 증가
- 추가한 항(L1 term)도 gradient descent algorithm의 최적화 대상에 속한다.
- L1 term을 제약조건(constraint)이라고 부르고 또는 Regularization term → L1 regularization
Ridge
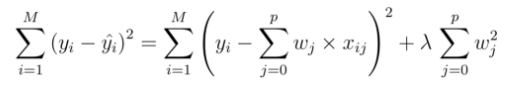
- 존재
- weight의 L2 term을 Loss function에 더해줌. (는 hyper-parameter)
- Loss가 무조건 증가
- 추가한 항(L2 term)도 gradient descent algorithm의 최적화 대상에 속한다.
- L2 term을 제약조건(constraint)라고 부르고 또는 Regularization term
→ L2 regularization
Conclusion
Lasso나 Ridge를 적용했을 때, 성능이 향상된다면Linear Regression 모델에 사용되는
feature vector가차원을 줄일 필요가 있다는 얘기가 됩니다.
→ feature selection이 성능 향상을 가져온다.- Regularization을 할 때, weight를 사용하는 방식을
weight decay- 학습에 제약조건을 지속적으로 가함
weight decay를 주게 되면,Gradient descent algorithm이 loss space를 탐색할 때 제약
조건을 받게 되는 효과가 있다 (청록색 영역)- 제약 조건 때문에, 특정 weight들이 사라지는 효과가 생기면서 (0에 가까워짐)
feature subset selection을 하는 효과가 있다.
XGBoost
**XGBoost: 하드웨어를 최적화 시킨 Gradient Boosting Model
(분류 & 회귀 모델)**Boosting & Gradient Boosting Model
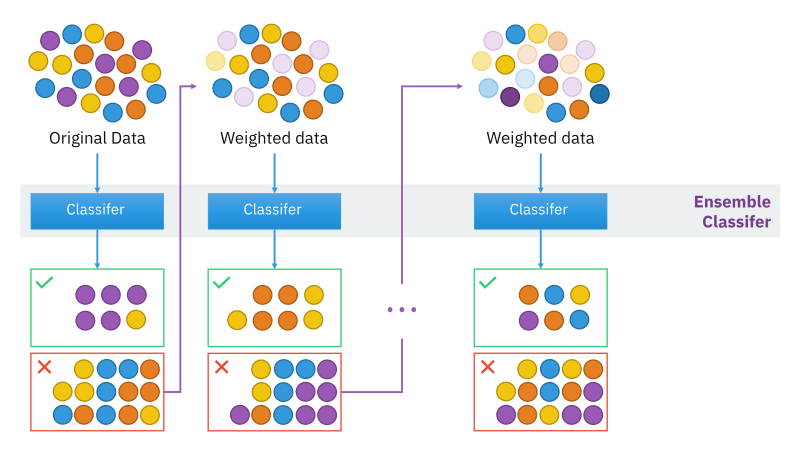
(https://en.wikipedia.org/wiki/Boosting_(machine_learning)#/media/File:Ensemble_Boosting.svg)
- Boosting model은 Bagging 방식이 만들어지는 원리가 전체 성능을 향상하는데 직접적인
연관이 없는 것을 보완한 모델입니다.
- 순차적 모델 - 첫번째로 만든 DT가 잘못 분류한 것을,
그 다음 DT가 보완하는 방식으로 순차적으로 Tree를 build - 다음 DT는 이전의 DT가 잘못 분류한 데이터들에 weight를 주는 것으로 DT가 뽑을 데이터
의sampling을 조절합니다.
이전의 데이터가 잘못 분류한 데이터를 지속적으로 보완하여 Aggregating하는 방식!
분류를 보완하는 것으로는 근본적인 성능 향상이 힘들기에 이를 보완하여 도입한 방식-
Gradient descent algorithm을 boosting model에 도입해서, 다음 DT가 이전 DT와 합쳐
져서더 적은 loss를 가지게 되는 방향으로 DT를 만드는 방법을
Gradient Boostingmodel이라고 합니다.→ But 위와 같은 방식은 좋지만 속도가 느리다는 단점이 있음
→ 이를 보완하기 위해 XGBoost를 도입
-
XGBoost
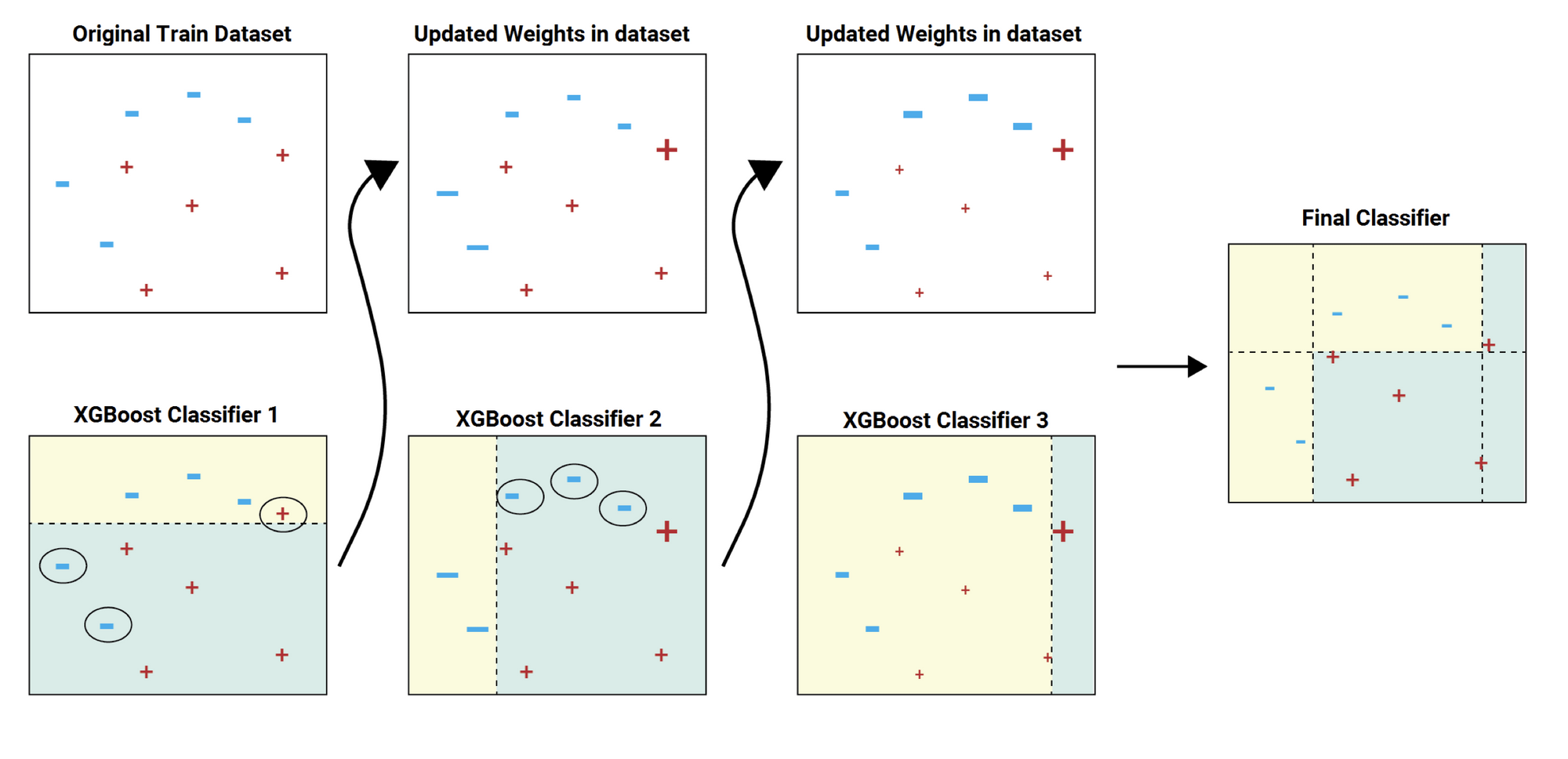
Gradient Boosting model(GBM) + System Optimization- tree의 best split point를 찾을 때, feature를 정렬하는게 가장 큰 cost가 소모됌
정렬하는 비용을 block 단위로 잘라서 update하는 방식을 제안하여 GBM(Gradient Boosting Model)과 거의 유사한 성능을 내는 방식을 제안한다- 훨씬 더 빠르게 정렬한 내용들을 사용할 수 있게 시스템 최적화한다.
GPU Acceleration, Cache awareness, I/O performance를 개선하여 훨씬 더 빠르게 학
습이 가능한 방식을 제안
- 하드웨어 측면에서 보완
Conclusion
XGBoost는 시스템 최적화를 통해서 practical한 좋은 솔루션을 제안한다
LightBGM
LightBGM : 기존 GBM들보다 훨씬 빠르게 학습이 되는 모델
(분류 & 회귀 모델)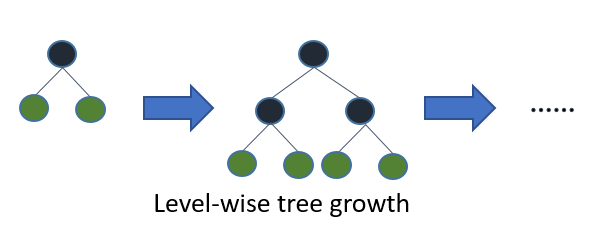
(https://lightgbm.readthedocs.io/en/latest/Features.html)
- 기존의 GBM들은 Level-wise 방식으로 tree를 build.
Level-wise이라는건 DT가 학습을 할 때, 같은 level에 있는 노드들을 모두 split한 뒤에 다 음 Level로 넘어가는 방식. (Breadth-First Search)( 위의 그림 참고)Depth가 커지면, ovefitting될 가능성이 높기 때문에, Level을 제한하여 최대한 모델을 키우는 방식을 사용해왔다. (Model Generalization)
- 해당 방식은 모두 분류를 한 뒤에 넘어가기에 속도적인 측면에서 느리다는 단점이 있다.
- Tree build에 있어서
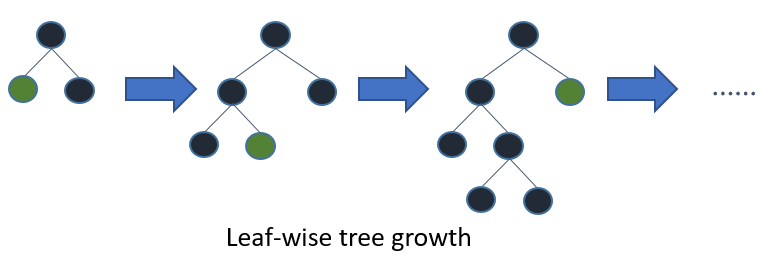
https://lightgbm.readthedocs.io/en/latest/Features.html
LightGBM이 제안하는 메인 아이디어는 Level-wise 방식이나 Leaf-wise 방식 모두 optimal을 만들게 된다면 비슷한 DT를 만들게 될 것이라는 점에서 착안.- Leaf-wise를 사용한다면,
훨씬 더 빠르게 optimal을 찾을 수 있다는 것이 핵심.- How?
→전체 Loss가 줄어드는 방향으로 node를 선정해서 split을 한다. 이 때, level을 유지하려는 경향을 포기합니다 (위의 그림 참고) - 필요한 노드들만 split하면 되기 때문에, 기존 GBM들과 비교했을 때
훨씬 빠르게 학습이 가능하다는 장점이 있다.
- How?
- 단, 적은 데이터를 사용하게 되면 overfitting이 될 가능성이 높아진다.
(10,000 rows 이상일 때만 사용 권장) - 또, 다른 GBM들에 비해 hyper-parameter sensitive하다.
(특히 max_depth에 가장 민감함)
회귀 모델 평가 지표
- MSE
- 값이 낮을수록 좋다
- RMSLE
- 값이 낮을수록 좋다
- MAE
- 값이 낮을수록 좋다
- R2 SCORE
- 모델의 설명정도, 발전 가능성에 대한 지표
- 1에 가까울수록 좋다
Classification
Classification(분류): 주어진 데이터(X)를 분류하고자 하는 값(y)에 할당하는 방법- 분류란, 주어진 Input data를 찾고자 하는 target value에 assign하는 것을 말한다.
- input data는 일반적으로 벡터이고, (feature vector) target value는 일반적으로 scalar (integer)
- 비슷한 특징을 가지는 데이터가 같은 분류로 나뉘어지는 것은 서로 상대적으로 가까운
feature vector들이 같은 target value를 부여받는 것이다 - 주어진 이미지는 feature vector로 표현이 됀다.
- 머신러닝 분류 모델을 거치면, inference 결과로 0 또는 1이 나오도록 하는 문제를
“ binary-classification ”
- Classification Model
- Linear Classifier
- Logistic Regression
- Naive Bayes
- KNN
- SVM
- Random Forest
- Neural Network
Linear classifier
Linear Classifier : y=Wx+b로 표시되는 선형 함수로 데이터를 분류하는 모델.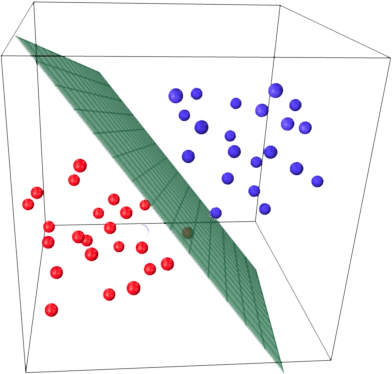
(https://www.kaggle.com/code/kashnitsky/topic-4-linear-models-part-2-classification/notebook)
linear classifier는 하나의 선형식(2차항 이상이 없는 $(y=Wx+b)$으로 데이터를 나누는 방법- 하나의 선형식으로 위/아래(1/0)로 공간이 나뉘기에 inference를 하게 되면 두 가지의 케이스로 데이터를 분류 가능
- 이 경계면을
decision boundary라고 하며, 이 경계면을linear classifier라고 한다. - 따라서,
linear classifier로 학습을 했다는건 데이터를 잘 나누는
적절한 파라미터 와 를 찾는 것
Logistic Regression
Logistic Regression : 주어진 데이터(X)를 통해서 사건의 발생확률(y)을 예측하는 통계 모델.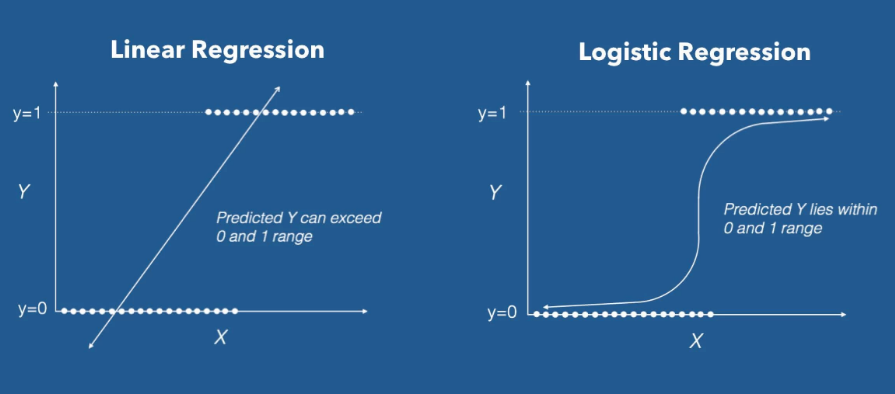
(http://incredible.ai/machine-learning/2016/04/26/Logistic-Regression/)]
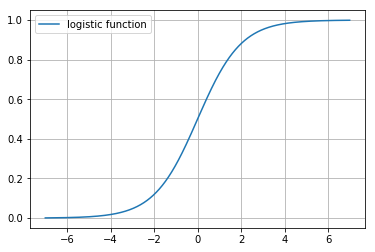
(http://incredible.ai/machine-learning/2016/04/26/Logistic-Regression/)
- Logistic Regression은 대표적인 이진(binary) 분류 모델
- Linear Regression을 분류 모델로 확장한 모델이다.
- Linear Regression 결과에 적절한 함수를 사용하여 output score를 0,1 사이의 값으로 변환하는 것으로 카테고리가 나올 확률을 예측하는 문제로 변환한다.
- 이 확률 값은 예측값이 1이 될 확률이고, 확률이 0.5를 넘기면 1로 예측하고 그렇지 않으면 0으로 예측하는 분류 모델로써 사용 가능하다.
SVM
서포트벡터머신(SVM):Decision Tree
Decision Tree: 조건에 따라 데이터를 분류하는 모델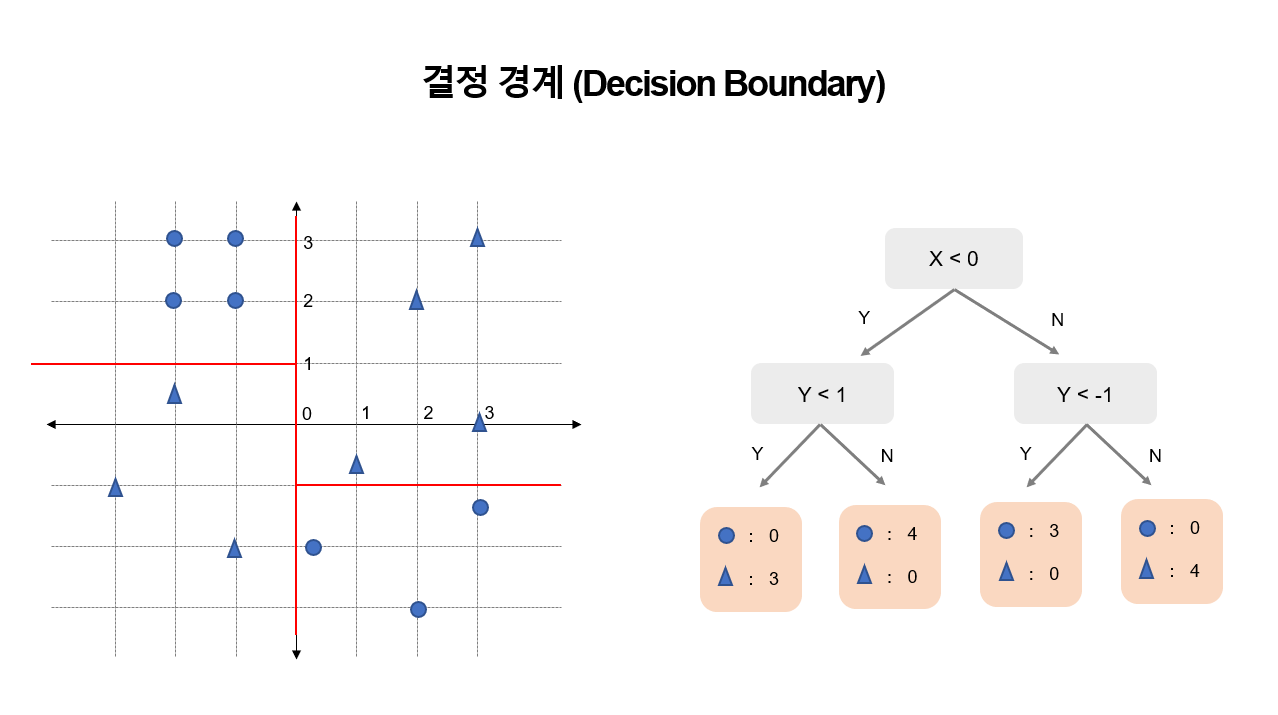
(https://lucy-the-marketer.kr/ko/growth/decision-tree-and-impurity/)
- Decision Tree는 대표적인
non-parametric과white-box모델- explainable,interpretable
- 현재 다루고 있는 모델은 CART ( Classification & Regression Tree)
해석력이 높은 모델 but 변동성(data,feature) 또한 매우 높다.- 최종 Node의 개수가 많아짐에 따라 overfit될 위험이 높다.
CART
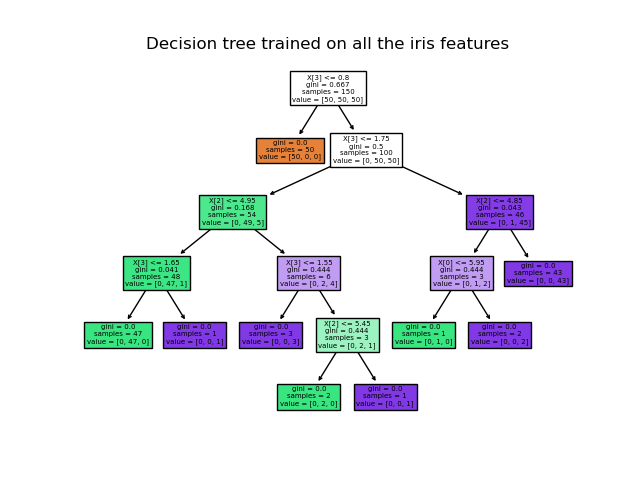
- CART는 대표적인 Decision Tree 모델 중 하나
(scikit-learn에 구현되어 있는 모델) - CART는 binary tree
- CART는 노드마다 feature 하나를 골라서 최적의 기준으로 나눌 수 있게 기준을 정한다.
이 때 최적이 되는 기준은Gini Criterion을 사용합니다. Gini Criterion은 불순도(impurity)를 의미- 불순도란 불순한 정도 즉 섞여있는 정도를 의미,
불순도가 제일 낮은 경우가 서로 제일 안 섞여 있는 경우
- 불순도란 불순한 정도 즉 섞여있는 정도를 의미,
Gini Criterion이 0이 될 때가 깔끔하게 나뉘어 있는 경우 (best case)
- CART모델은 Gini criterion이 가장 작아지는 포인트를 찾아서, 데이터를 나눈다.
최적의 tree를 찾는데 NP-complete문제이기에 Heuristic한 방식을 찾는다
Inference
- 만들어진 DT에 test data를 넣어서, 트리를 탐색(retrieve)하게 되면 최종 결과가 나오게 됌
- 이 결과를 예측값으로 사용하여 분류
장단점
- 장점 :
- white box model (학습 결과가 클리어하게 해석 가능하다)
- easy to train(학습이 쉽다)
- 단점 :
- easy to overfit(쉽게 training data를 외우게 됌)
- Tree를 통해 계속 분류하다보면, 모두 나눌 수 있는 상황이 발생하기에
- training data가 조금만 바뀌어도 학습 모델이 전혀 다르게 형성
- data가 바뀜에 따라, 분류 모델 또한 변경됀다.
- easy to overfit(쉽게 training data를 외우게 됌)
Decision Tree는 Train_data에 의존적이고, 이에 따라 모델이 변하는 경우가 발생한다.
→ 이를 해결하기 위한 방안으로 Random Forest 가 존재
Random Forest
Random Forest: Decision Tree가 모여서 더 좋은 결과를 내는 모델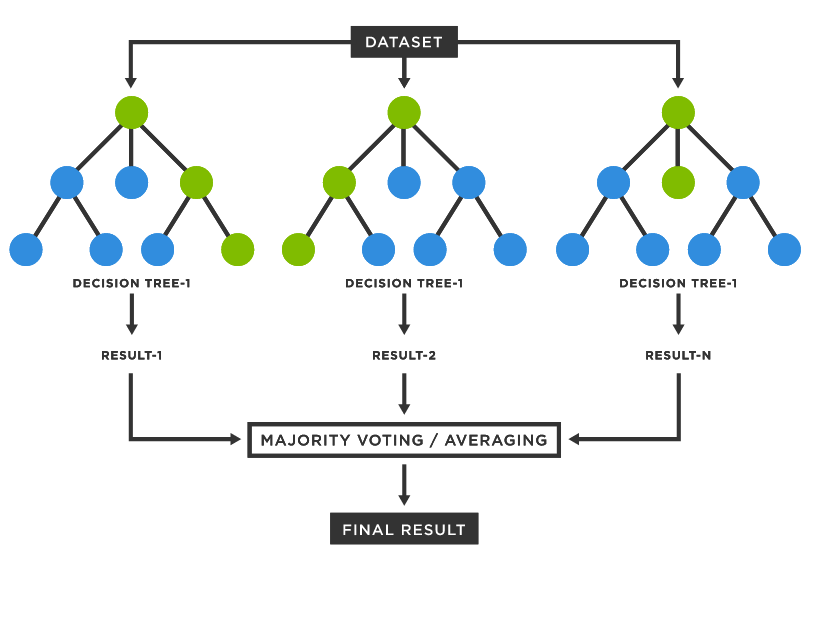
(https://www.tibco.com/reference-center/what-is-a-random-forest)
- Random Forest는 CART 모델이 가지는 단점을 극복하기 위해 제시된 모델
- DT 하나가 training data에 쉽게 overfit되고, data,feature 변화에 민감하기 때문에 여러 개를 사용해서 다수결을 하는 방식으로 보완하는 방식
- practical하게 굉장히 좋은 성능을 보여줌
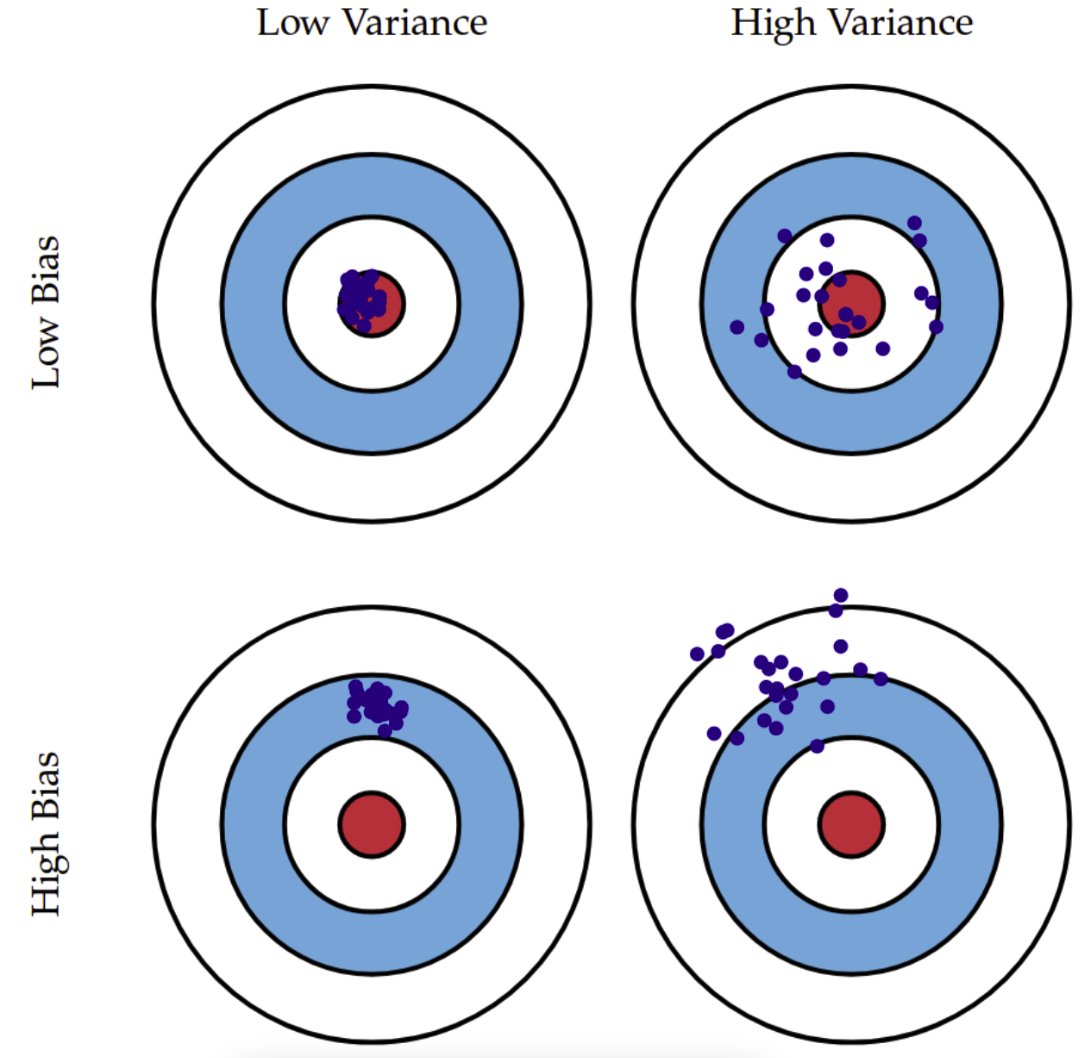
-
Bias는 데이터 내에 있는모든 정보를 고려하지 않음으로 인해, 지속적으로 잘못된 것들을 학습하는 경향 → →Underfitting -
Variance는데이터 내에 있는 에러나 노이즈까지 잘 잡아내는highly flexible models 에 데이터를
fitting시킴으로써, 실제 현상과 관계 없는 random한 것들까지 학습하는 알고리즘의 경향을 의미→
Overfitting
-
Low bias & Low variance → Ideal
-
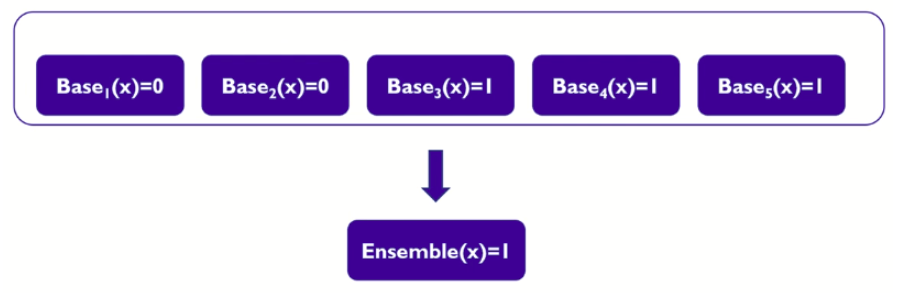
이와 같이 단일모델(CART)을 여러 개 모아서 좋은 판단을 하는 방법론을
Model Ensemble이라고 한다.-
여러 모델의 예측을 다수결 법칙 or 평균을 이용해 모델을 통합하여 하나의 모델로 만드는 방법.→ 성능이 좋아짐
- Base 모델이 서로 독립적일때 ( 앞, 중간, 뒤 데이터를 각각 학습을 잘한다)
- 1111 222 333 ( 1 앞 2 중간 3 뒤)
- Base 모델의 무작위 예측을 하는 것보다 모델의 성능이 좋을 때
- Base 모델이 서로 독립적일때 ( 앞, 중간, 뒤 데이터를 각각 학습을 잘한다)
-
- Decision Tree를 그저 모을 경우 좋은 결과를 낼 수 없음
- 동일한 data에 대해서 만들어진 DT는 같은 결과를 출력
- 동일한 best split point가 뽑히기 때문 → 다양성 必
- 동일한 data에 대해서 만들어진 DT는 같은 결과를 출력
- 다양성을 주기 위한 2가지 방법
Bagging( Bootstrap Aggreagating)→ data sampling(모집단 변경)- Bootstrap : 데이터가 원본 개수랑 똑같은데 확률 분포가 약간 바뀜
(복원추출) - Aggregating : 합침
- 다수결
(Hard Voting) → 각 모델의 성능을 독립적으로 생각 - 가중평균
(Soft Voting)→ 각 모델의 성능을 믿음 - 확률
- 다수결
- bagging: 많이 뽑힌 것을 뽑는다
- Bootstrap : 데이터가 원본 개수랑 똑같은데 확률 분포가 약간 바뀜
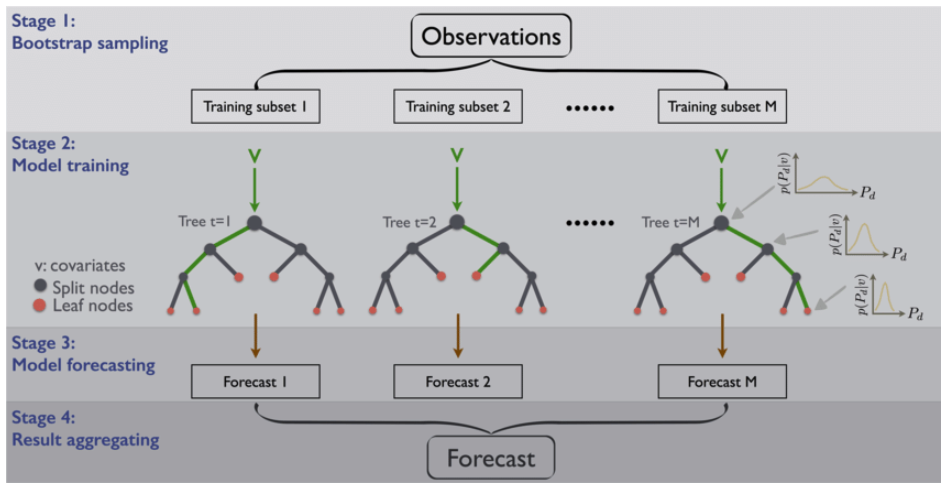
Random subspace Method→ feature sampling ( DT가 뽑는 feature를 바꿈)
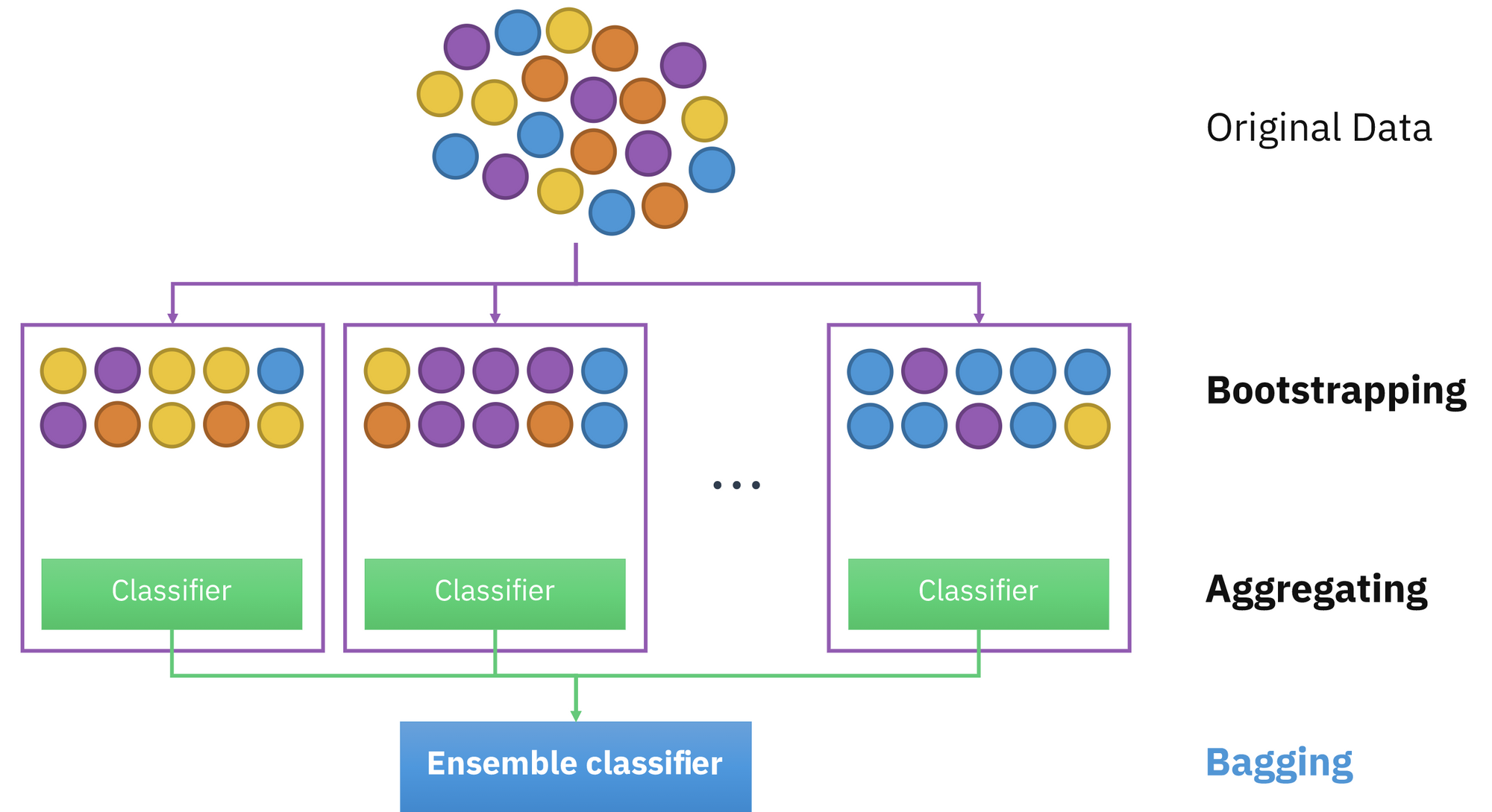
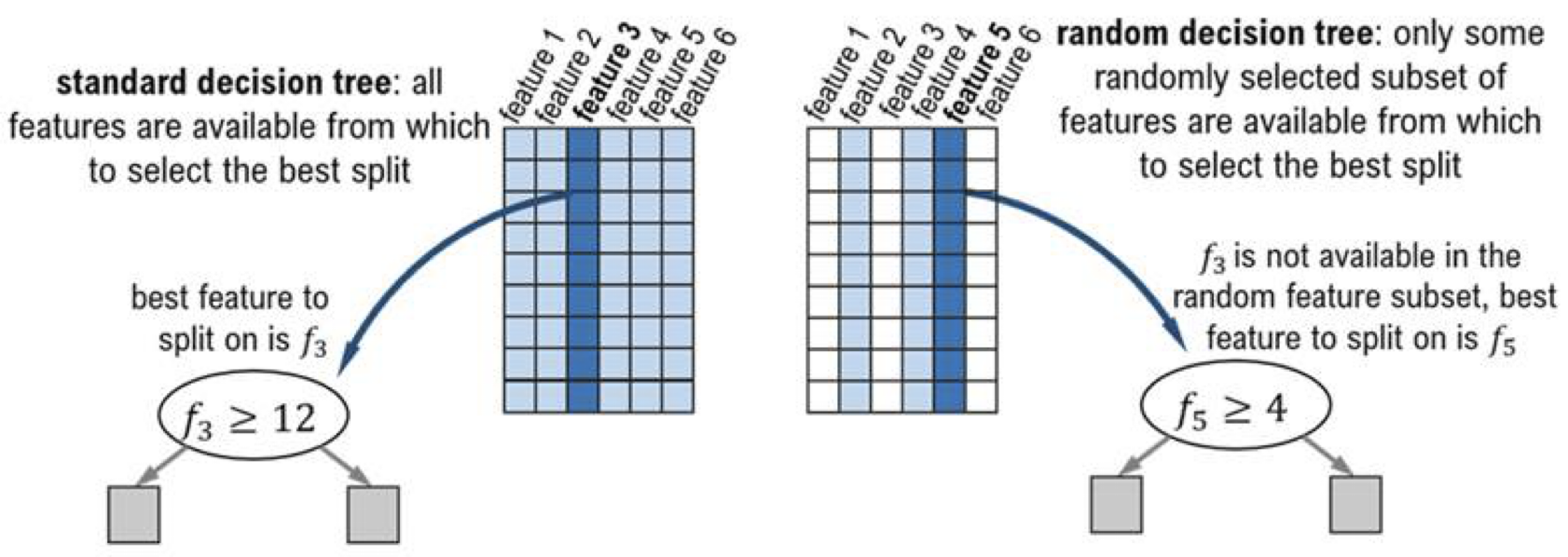
- data sampling + feature sampling을 통해서 만들어진 각 DT에 다양성을 제공
- 각 DT를 학습할 때마다, Bootstrapping과 Random Subspace method를 적용
- 몇 개의 DT를 모을지를 정하는 것은
hyper-parameter - 이렇게 만들어진 DT들의 결론을 다수결로 평가하는 것으로
“집단 지성"을 구현 가능하다. Random Forest는 그냥 DT들을 모으는게 아닌,randomness를 적당히 포함하는 것으로DT의 약점을 잘 보완한모델
- 정형 데이터를 머신러닝으로 수행할 때 굉장히 좋은 baseline model(만만하게 잘되는 모델)
Random Forest는 DT들의 모임이기 때문에 어느정도 explainability를 가지고 있다.!
Clustering(군집 분류)
**Clustering : 주어진 데이터(x) 사이의 유사한 데이터들을 묶어주는 방법**- 클러스터링이란, 비슷한 데이터들끼리 같은 그룹으로, 그렇지 않은 데이터들은
다른 그룹으로 묶어주는 방법 - 클러스터링은 대표적인
unsupervised learning - input data는 일반적으로 벡터이며, (feature vector)
target value(y)는 없다.- target value가 없다보니, feature vector가 굉장히 중요하다
→ feature engineering의 영향을 많이 받는다
- target value가 없다보니, feature vector가 굉장히 중요하다
- 클러스터링에서는 주어진 데이터를 가지고 판단하는 수밖에 없기 때문에,
2가지 요소가 정말 중요!feature vectorsimilarity
K-means
**K-means: 주어진 데이터에서 k개의 중심점을 찾아서 데이터를 묶어주는 방법**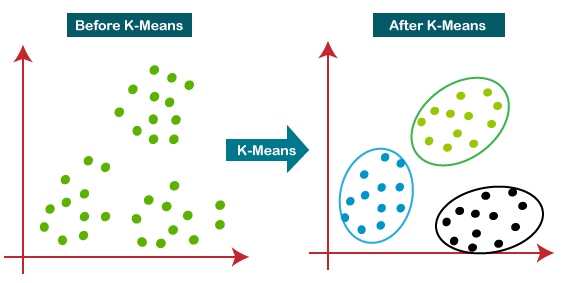
(https://www.analyticsvidhya.com/blog/2021/04/k-means-clustering-simplified-in-python/)
- 모델이 직관적이고 간단하며 빠르다.
- cluster에서 가장 많이 사용되는 모델
- Random serach, Grid search를 통해 적절한 클러스터 개수를 찾아나가야함
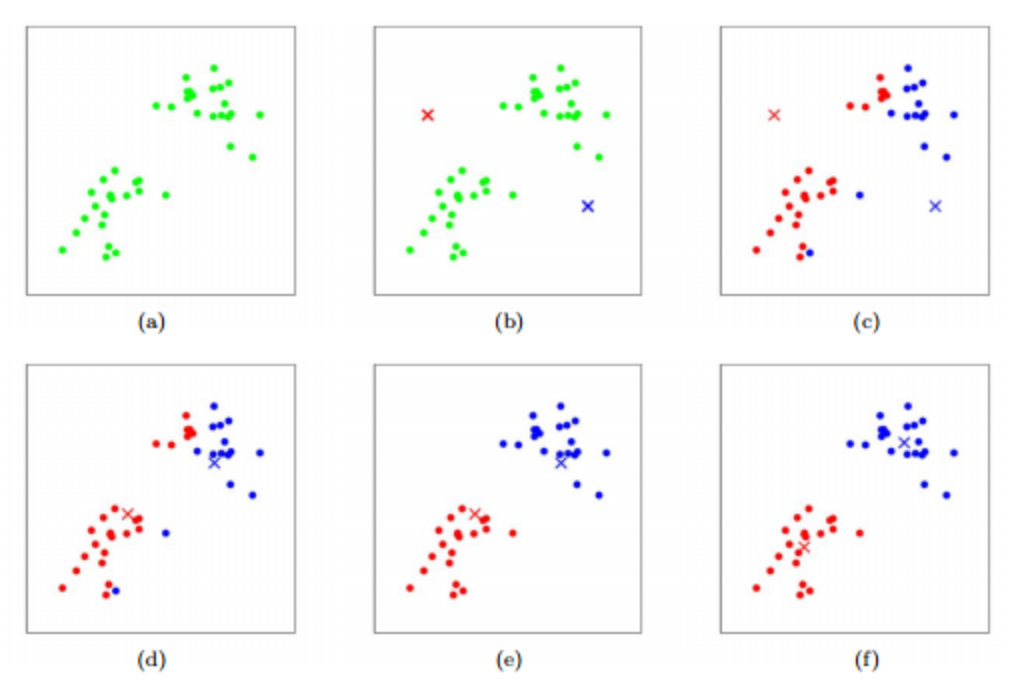
(https://hleecaster.com/ml-kmeans-clustering-concept/)
- 주어진 데이터에서 랜덤으로 K개의 데이터를 첫 기준점(
centroid)으로 잡는다.
각centroid에 0번부터 차례대로 번호(cluster label)를 부여한다. - 각 데이터는 K개의 centroid중에 가장 가까운 centroid를 찾아서 같은 번호를 부여 받는다.
- 같은 번호인 데이터들끼리 평균(mean)을 계산한다.
- 각 평균을 새로운 centroid로 지정한다.
- 2번부터 다시 반복하고. 더 이상 cluster label이 바뀌는 데이터가 없다면 알고리즘이 종료됀다.
장단점
- 장점
- 아주 빠름
- 모델 수행원리가 간단하여 해석이 용이
- unsupervised learning은 해석이 굉장히 중요!
- objective function이 convex라서 무조건 수렴한다.
- 단점
- mean을 기준으로 하기 때문에
outlier에 굉장히 취약하다. ( 미리 제거하고 수행할것) - 무엇을 기준으로 나누어졌는지는 알기 힘들다. (data를 하나씩 까보지 않는 이상…)
- 평가 방법기준에 따라 잘 나누어졌는지 아닌지는 확인 가능하다.
- 데이터의 모양이 hyper-spherical이 아니라면 잘 묶이지 않는다.
- initial centroid를 어떻게 고르냐에 따라서 성능이 천차만별로 달라진다.
- 위의 그림 (b)를 참고하면 이해 빠름
- K-means++으로 어느정도 개선함
- K가 hyper-parameter이다.
- mean을 기준으로 하기 때문에
Hierarchical Agglomerative
HAC : 데이터를 유사한 순서대로 묶어서 계층구조를 만드는 방식으로 데이터를 묶어주는 방법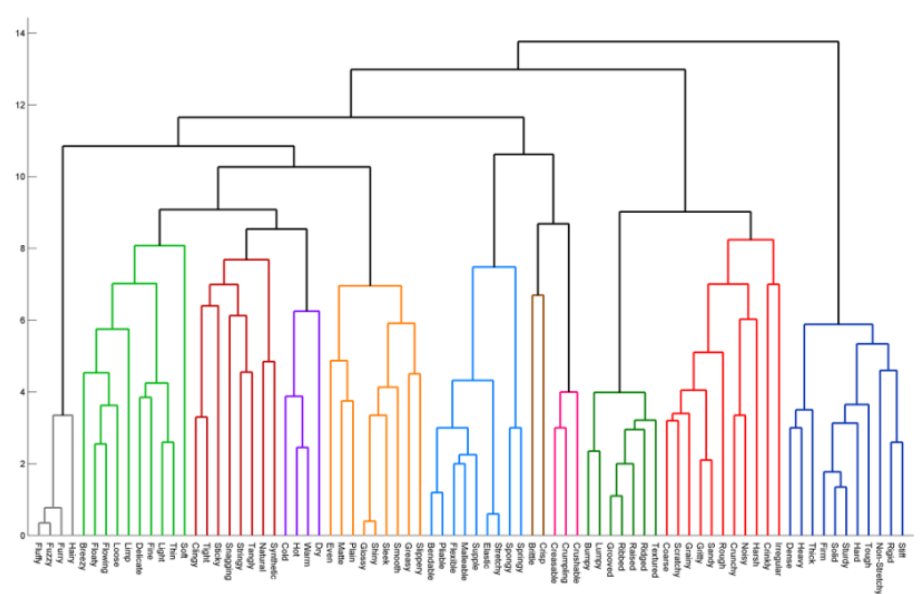 (https://ratsgo.github.io/machine%20learning/2017/04/18/HC/)
(https://ratsgo.github.io/machine%20learning/2017/04/18/HC/)
- HAC는 상향식 계층 클러스터링
- 아래 → 위로 점차 데이터를 묶어가는 방식
- 위와 같은 그림을
Dendrogram이라고 부른다. - Dendrogram에서 x축은 데이터 하나하나를 의미하고, y축은 유사도를 나타낸다.
- 모든 데이터간 유사도를 계산해야하므로 속도가 느리다.
Algorithm
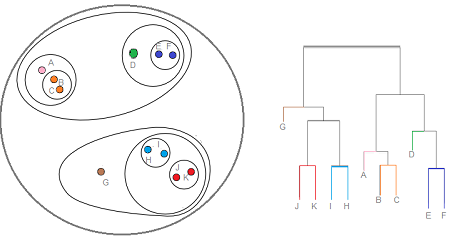
(https://www.statisticshowto.com/hierarchical-clustering/)
오른쪽이 Dendrogram
- 모든 데이터를 독립적인 클러스터로 세팅한다.(서로 다른 n개의 cluster label을 부여받는다)
- 유사도와 묶는 방식을 정한다.
- 가장 유사도가 높은 2개의 클러스터를 고른다.
- 정해진 방식으로 묶는다. (single의 경우 가장 가까운 데이터의 pair가 포함된 두 개의 클러스터를 합친다)
- 모든 데이터가 묶여서 하나의 클러스터가 될 때까지 3,4번을 반복한다.
이때 모든 데이터가 묶이면 dendrogram을 그릴 수 있다. - dendrogram에서 특정 threshold(distance)를 기준으로 세로로 잘랐을 때, 나뉘는 클러스터들을 최종 클러스터로 선정한다.
Linkage criteria
- Single : 가장 가까운 데이터 Pair가 포함된 두 개의 클러스터를 합칩니다.
- Average : 클러스터 간의 평균 거리가 가장 가까운 두 개의 클러스터를 합칩니다.
- Complete : 임의의 두 개의 클러스터 중에 가장 멀리있는 데이터간의 거리가 가장 가까운
두 개의 클러스터를 합칩니다. (minimax) - Ward : 모든 클러스터들의
within cluster variance가 최소가 되는 클러스터들을 합칩니
다.
1. within cluster variance란, 클러스터 내부의 데이터간의 sum-of-squared distance를 의미
사실 Ward criterion을 사용하면, K-means와 유사한 방식으로 묶어주게 됩니다.
장단점
- 장점
- 원하는 유사도와 linkage를 사용할 수 있기에, 다양한 공간과 형태의 클러스터를 찾을 수 있다.
- Dendrogram을 이용해서, 데이터에 따라 유연하게 최적의 클러스터 개수를 정할 수 있다.
- 거리 지정
- 어떤 linkage 방법을 사용하더라도, 한번에 하나씩 클러스터가 줄어들기 때문에 원하는 클러스터 개수를 찾을 수 있다.
- 단점
- K-means에 비하면 많이 느리다.
- 대용량 데이터에 적합하지 않음
DBSCAN
DBSCAN: 정의한 밀도에 따라 인접한 데이터를 계속해서 묶어나가는 방법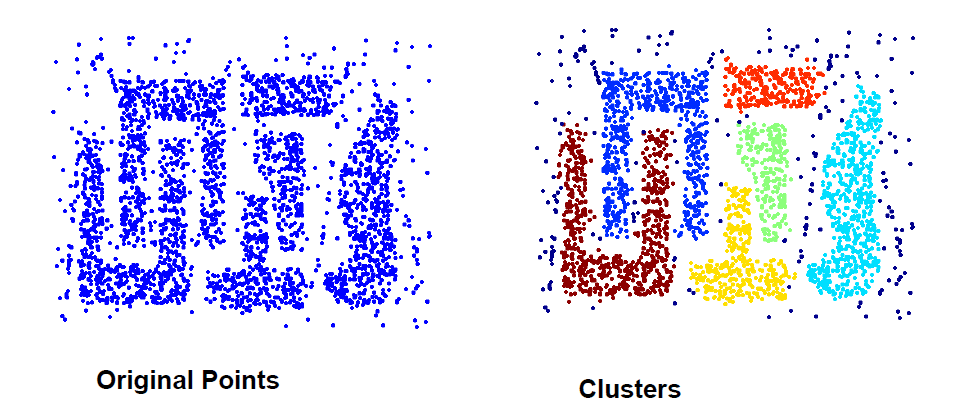
(https://lucy-themarketer.kr/ko/growth/%ED%81%B4%EB%9F%AC%EC%8A%A4%ED%84%B0%EB%A7%81%EA%B3%BC-dbscan/)
- DBSCAN은
밀도라는 개념을 도입하여, 서로 가까이 있는 데이터들을 하나의 클러스터로 묶어준다. - DBSCAN은 이전 기법들과는 다르게 noise data를 outlier로 취급하여 분류한다. (outlier detection)
- outlier를 찾는 문제에 활용됀다.
- e.g: 불량품 검출, 사기거래감지
- outlier를 찾는 문제에 활용됀다.
Algorithm
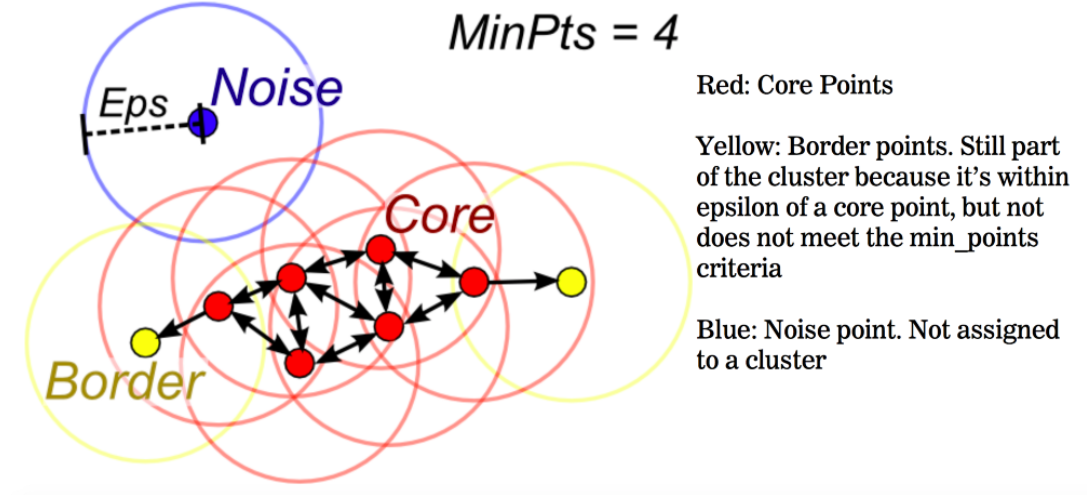
(https://medium.com/@agarwalvibhor84/lets-cluster-data-points-using-dbscan-278c5459bee5)
- 밀도를 정의하기 위한 파라미터
MinPts와 Eps를 정의한다- Eps는 같은 묶음으로 판단하는 기준이 되는 거리값 (euclidean distance 기준)
적절한 Eps값을 예측하기 위해서 KNN이 선행되면 좋을 것으로 예상
MinPts는 같은 묶음으로 판단하기 위해서Eps를 반지름으로 하는 원을 그렸을 때, 최
소한으로 포함되어야 하는 데이터의 개수 (range query)
- Range query: 범위를 만족하는 쿼리 (지도상 내 주변에 위치한 스타벅스의 개수)
- e.g: Minpts=4이고 4개 이상 있을 때, 그 때 하나라고 말할 수 있다
- Eps는 같은 묶음으로 판단하는 기준이 되는 거리값 (euclidean distance 기준)
- 각 데이터를 기준으로 Eps 크기를 가지는 원을 그려서 그에 해당하는 데이터를 찾는다.
(range query) Range query의 결과로 MinPts 이상의 데이터가 포함된다면, 그 데이터를
Core point라고 지정한다. - Core Point와 연결된 모든 Core Point들은 하나의 클러스터로 묶인다
- 만약, 어떤 포인트가
range query를 했을 때 MinPts를 만족하지 못하지만, Range query 의 결과에 Core Point가 포함되어있는 경우엔 해당 포인트는 Border Point가 됀다 - Border Point까지는 하나의 클러스터로 묶인다.
Core Point, Border Point를 모두 만족하지 못하는 데이터는 Noise Point (Outlier)로 판단이 되며, 이 때 -1의 cluster label을 부여받는다.
장단점
- 장점
- 다양한 형태의 데이터에서 클러스터를 잘 파악한다. → 성능이 좋다 →
K-means를 사용하기 전에 먼저 DBSCAN을 활용하여 대략적인 k값을 잡아보고이를 기준으로 K-means에 대입하여 K 초기값의 범위를 줄여 볼 수 있다.
- 어떻게든 다른 클러스터에 모든 데이터를 포함시키는 다른 방법들과는 달리 outlier를 정의하기 때문에
만들어진 클러스터의 품질이 좋다 ( 해석력이 뚜렷)
- 다양한 형태의 데이터에서 클러스터를 잘 파악한다. → 성능이 좋다 →
- 단점
- Minpts & Eps가 hyper-parameter
- 모든 포인터에 range query를 계산해야하므로 속도가 느린 편 →
- 고차원 공간에서 성능이 떨어지는 단점이 있다.
Spectral Clustering
Spectral Clustering: KNN Graph를 생성하여 데이터의 특징을 잘 파악한 뒤
성능이 좋은 클러스터를 생성해주는 방법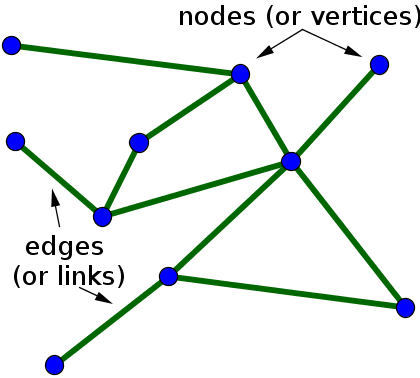
(https://velog.io/@keum0821/%EA%B7%B8%EB%9E%98%ED%94%84Graph%EB%9E%80)
- 데이터 간의 관계를 모델링 할때 사용하는 자료구조를 Graph라고 한다.
- Node와 Edge로 구성되어 있다.
- Social Network 나 Molecular Structure가 대표적인 Graph를 활용해서 해석할 수 있는 도메인
- 추상적 관계를 모델링하는 것이 Graph
Spectral Clustering
- 대표적인 Graph Clustering 기법 ( 묶이는 대상이 subgraph(node))
- 주어진 데이터를 그래프 모델로 해석하여, subgraph로 데이터를 나누는 것으로 묶어주는 방식
- 각 데이터를 노드로 두고, 각 데이터로부터 보다 가까운 거리에 있는 노드들을 연결한
KNN Graph를 만든다. - 만든 그래프가 가장 잘 나눠지는 곳을 찾아서 그래프를 2분할 한다. (find min-cut)
- 원하는 개수의 클러스터(subgraph)가 생길 때까지 그래프를 분할한다
(만약, 찾고자 하는 클러스터가 5개라면 분할을 4번 진행하면 됀다.)
장단점
- 장점
- 기존 공간에 구애받지 않고 데이터를 그래프 구조로 파악하는 것으로 성능이 꽤 좋다.
- 단점
- KNN Graph를 만들고 min-cut을 찾는게 시간이 오래 걸린다. →
K-fold
K-fold (병렬학습) :교차 검증을 통해 모델의 과적합 정도를 판단할 수 있다.- 장점
- 특정 데이터셋의 Overfit 방지
- 데이터셋의 규모가 적을 때, 과소적합 방지
- 일반화된 모델 생성 가능
- 단점
- 모델 훈련 & 평가 소요시간 증가( 반복학습 횟수 증가) →
병렬학습 시계열 데이터에서 사용하면 안됌!!k-fold학습을 통해 섞어버린다면, 시계열의 특징인 연속성, 즉 순서가 사라지기 때문에
- 모델 훈련 & 평가 소요시간 증가( 반복학습 횟수 증가) →
LightGBM Regressor
Image feature vector
Text feature vector
Machine Learning 프로세스
문제정의
- 데이터수집
- 데이터탐색
- 데이터전처리
-
dummy란?
→ 데이터가 왜곡되지않도록 하는 작업, 추후에 다시 다뤄볼 예정.
-
- 모델링
- 모델평가
- 결과보고서 작성
