(2020/11/03 작성)
Introduction
추천 시스템은 수 많은 아이템 중에서 사용자가 좋아할만 한 소수의 아이템을 제공합니다. 더욱 나은 추천을 하기 위해서는 "좋은 추천 시스템"이라고 평가할 수 있어야 하며, 이에 사용되는 평가 지표는 다양합니다. 이 글에서는 추천의 정확도를 평가하는 평가 지표 중 자주 사용되는 5개 (Precision, Recall, NDCG, MAP, MRR)를 정의하고 간단한 예제 코드로 살펴보겠습니다. 수식은 아래 논문에서 차용하였습니다.
Example & Notations
앞으로 이야기는 한 명의 사용자를 대상으로 할 것이며, 전체 지표는 각 사용자 지표의 평균으로 구할 수 있습니다.
먼저, 앞으로 사용할 Notation을 정의하겠습니다. n개의 아이템을 가진 시스템에서 추천 시스템은 아이템을 사용자가 좋아할만 한 순서로 정렬 (Ranking)합니다. 이를 P라고 합니다. 이 중, 사용자가 실제로 좋아하는 아이템 T의 P에서의 위치를 R이라고 정의합니다.
예를 들어, P=[4,6,2,3,1,8,10,9,5,7]이고 T={1, 6, 9}라면, R={2 ,5, 8}이 됩니다. (Index가 1부터 시작한다고 가정)
위 정의에 따르면, 추천 시스템은 사용자의 정보를 입력받아 좋아하는 아이템의 위치 R을 출력하고, 임의의 Metric M은 R을 평가 지표로 변환합니다.
Definitions
General Form
이제 위 정의 아래에서 5가지 지표를 정의해보겠습니다.
Precision은 "상위 k개 추천에 정답이 얼마나 포함되어있나?" 를 측정하며 (상위 k에 포함된 정답 수 / k)로 계산합니다. Recall은 "정답 중 얼마나 상위 k에 포함되어있나?"를 측정하며 (상위 k에 포함된 정답 수 / 정답 수)로 계산합니다. 이 둘은 집합의 개념으로 추천 및 정답의 순서를 고려하지 않는 평가지표입니다.
5개 지표의 수식은 아래와 같습니다. \delta(cond)는 condition이 참이면 1, 거짓이면 0을 반환합니다.
NDCG는 "가장 이상적인 추천에 얼마나 가까운가?"의 개념으로 1등부터 순서대로 모두 정답인 Ideal DCG로 실제 DCG를 나눕니다. 이 지표는 순서를 고려하여 높은 순위에 정답이 있을 수록 값이 큽니다. (M)AP는 "상위 k의 Precision의 평균"으로 계산하며 (M)RR은 "정답 중 가장 순위가 높은 아이템 순위의 역수" 입니다. 이들은 정답이 상위 k중 상위에 있을 수록 높습니다.

Leave-one-out
추천 시스템의 평가에는 다양한 프로토콜이 활용되는데, 각 사용자별 정답 아이템이 1개인 Leave-one-out 또한 자주 사용됩니다. 이 경우에도 위 수식으로 계산 가능하지만, |R|=1이라는 점을 고려하면 아래와 같이 식을 단순화 할 수 있습니다.
이 때, Recall은 k개 안에 정답이 들었는지 유무만을 보게 되며 흔히 Hit Ratio (HR)이라는 이름으로 사용됩니다. 또한, MAP는 MRR과 식이 같아집니다.
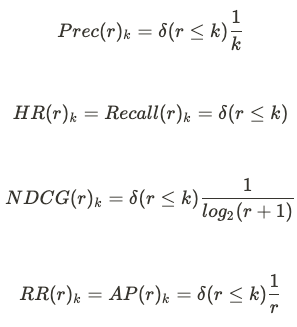
Implementation (k=5)
이제 위 수식을 코드로 구현해보겠습니다. 구현은 일반적인 경우(holdout)와 Leave-one-out으로 나누어서 구현해보겠습니다. k는 5로 고정합니다.
CASE 1: General Form
추천 시스템이 예측한 정답 위치는 R={2,5,8}이라고 해보겠습니다. 상위 5개 안에 드는 것은 2와 5, 두 위치에 있습니다. Precision=2/5=0.4 라고 쉽게 계산할 수 있습니다.
5개 지표에 대한 구현과 결과는 아래와 같습니다. numpy를 이용하면 쉽게 구현할 수 있습니다.
print('>>>> General')
P = np.array([4, 6, 2, 3, 1, 8, 10, 9, 5, 7])
top_k=5
def precision_k(R, k):
num_hits = np.sum(R <= k)
prec_k = num_hits / k
return prec_k
def recall_k(R, k):
num_hits = np.sum(R <= k)
recall_k = num_hits / len(R)
return recall_k
def ndcg_k(R, k):
# NDCG
idcg = 0.0
for i in range(min(len(R), k)):
idcg += 1 / np.math.log2(i + 2)
dcg = 0.0
for i in range(k):
if (i + 1) in R:
dcg += 1 / np.math.log2(i + 2)
ndcg_k = dcg / idcg
return ndcg_k
def ap_k(R, k):
ps = 0
for i in range(k):
if (i + 1) in R:
ps += precision_k(R, i + 1)
ap = ps / min(len(R), k)
return ap
def rr_k(R, k):
min_pos = min(R)
rr = 1 / min_pos if min_pos <= k else 0.0
return rr
T = np.array([1, 6, 9])
R = np.where(np.isin(P, T))[0] + 1
# R = np.array([2, 5, 8])
metrics = {
f'Prec@{top_k}': precision_k(R, top_k),
f'Recall@{top_k}': recall_k(R, top_k),
f'NDCG@{top_k}': ndcg_k(R, top_k),
f'AP@{top_k}': ap_k(R, top_k),
f'RR@{top_k}': rr_k(R, top_k)
}
for k, v in metrics.items():
print(k,':',v)
""" Expected Output
>>>> General
Prec@5 : 0.4
Recall@5 : 0.6666666666666666
NDCG@5 : 0.4776237035032179
AP@5 : 0.3
RR@5 : 0.5
"""CASE 2: Leave-one-out
이번에는 정답이 3 (세번째)에 1개 들어있다고 가정하겠습니다. 이 경우, Precision은 0.2, Recall(HR)은 1.0이 됩니다. 구현을 보면 한결 간단해진 것을 알 수 있습니다.
print('>>>> Leave-one-out')
def precision_loo_k(r, k):
hits = float(r <= k)
prec_k = hits / k
return prec_k
def recall_loo_k(r, k):
recall_k = float(r <= k)
return recall_k
def ndcg_loo_k(r, k):
hits = float(r <= k)
ndcg_k = hits * (1 / np.math.log2(r + 2))
return ndcg_k
def ap_loo_k(r, k):
hits = float(r <= k)
ap = hits / r
return ap
T = 2
r = int(np.where(P == T)[0] + 1)
metrics = {
f'Prec@{top_k}': precision_loo_k(r, top_k),
f'Recall@{top_k}': recall_loo_k(r, top_k),
f'NDCG@{top_k}': ndcg_loo_k(r, top_k),
f'AP@{top_k}': ap_loo_k(r, top_k)
}
for k, v in metrics.items():
print(k,':',v)
""" Expected Output
>>>> Leave-one-out
Prec@5 : 0.2
Recall@5 : 1.0
NDCG@5 : 0.43067655807339306
AP@5 : 0.3333333333333333
"""Wrapping Up
이번 글에서는 추천 시스템 평가에 활용되는 다양한 정확도 지표에 대해서 정리 및 구현을 했습니다. 추천의 정확도도 중요하지만 다양성 또한 중요하게 고려되어야 합니다. 다음에는 (언젠가) 다양성 지표를 정의, 구현을 해보겠습니다.
