Introduction to Probability and Probability Distributionn - Week 1
Lesson 1 - Introduction to Probability
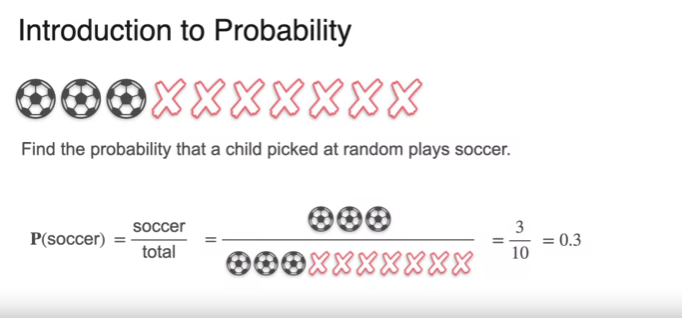
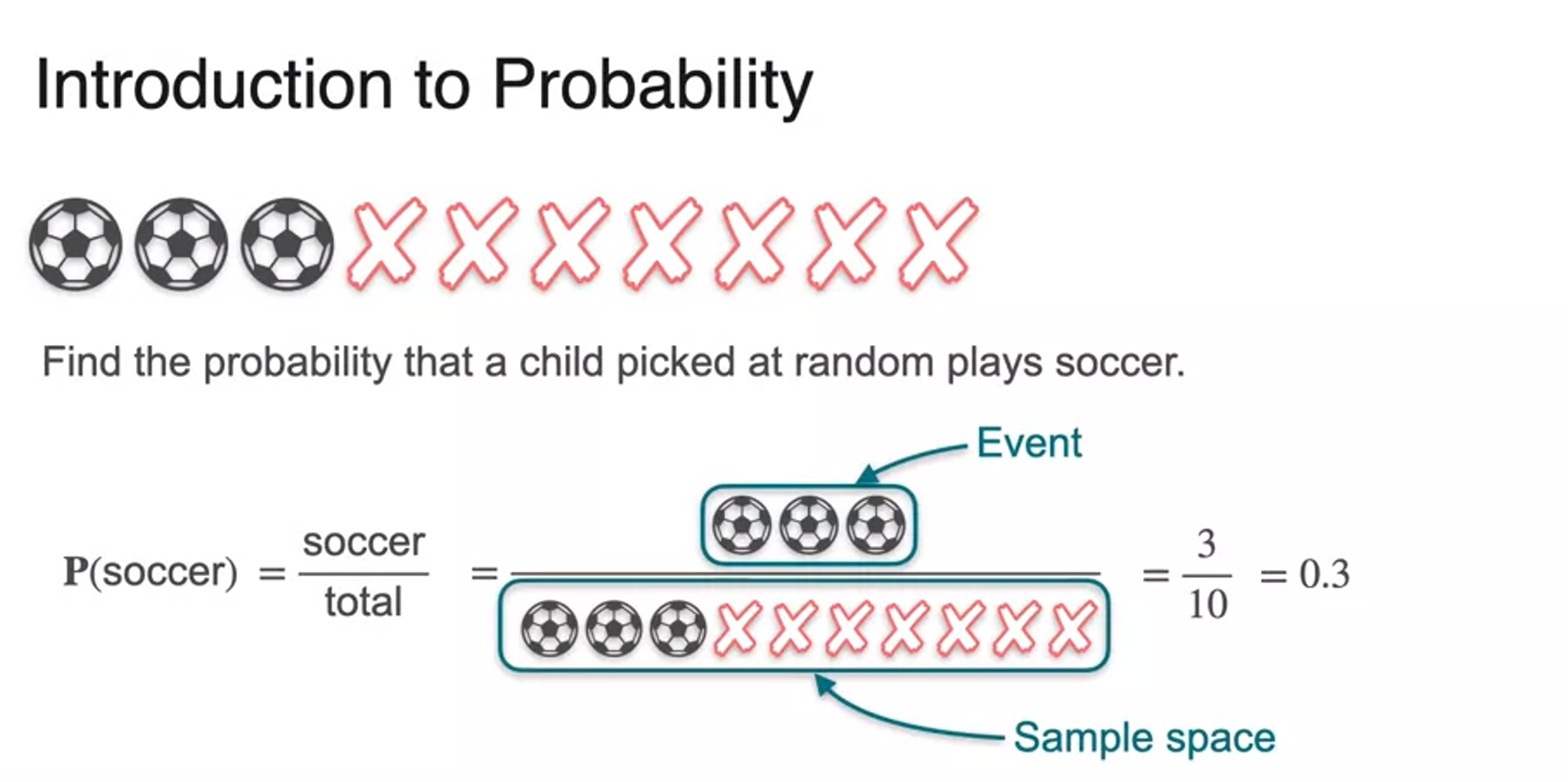
What is Probability?

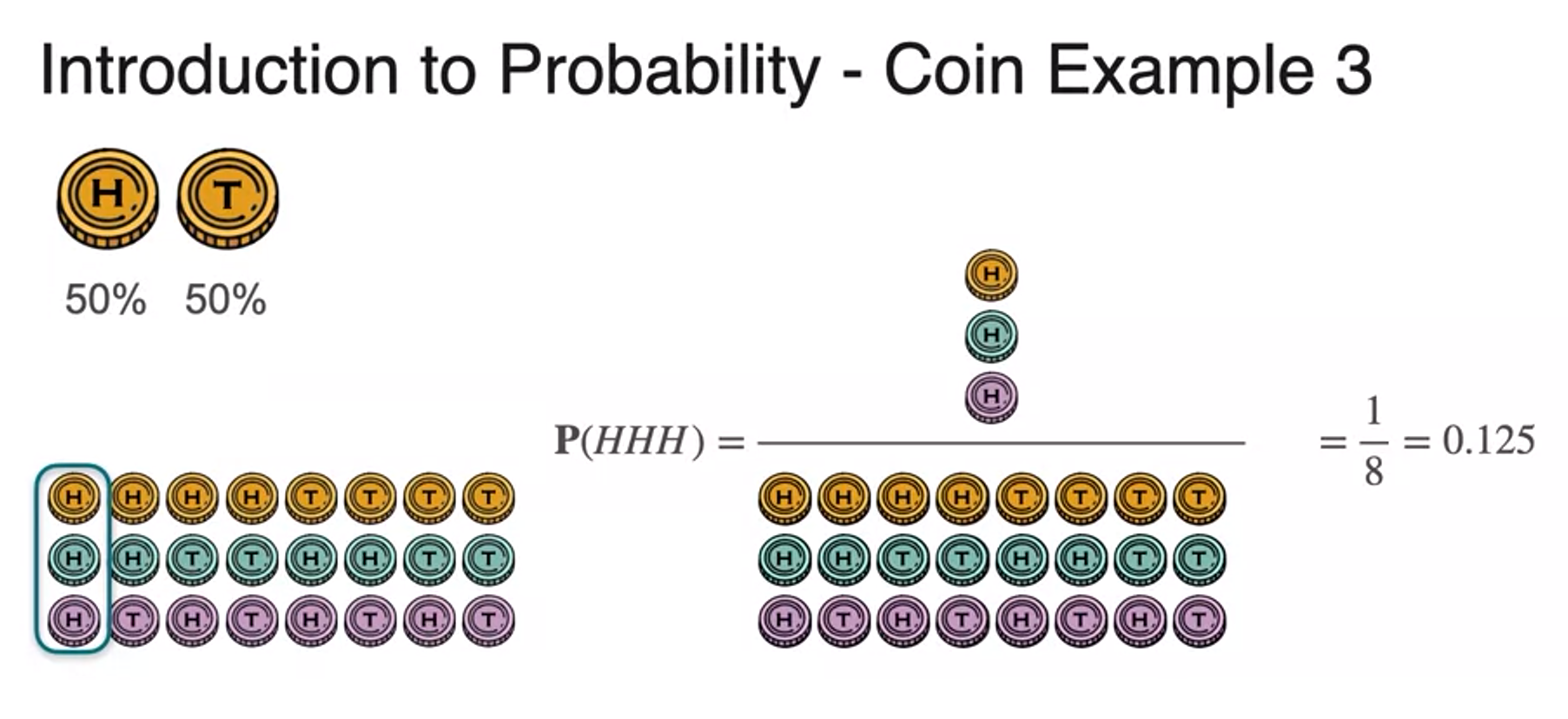
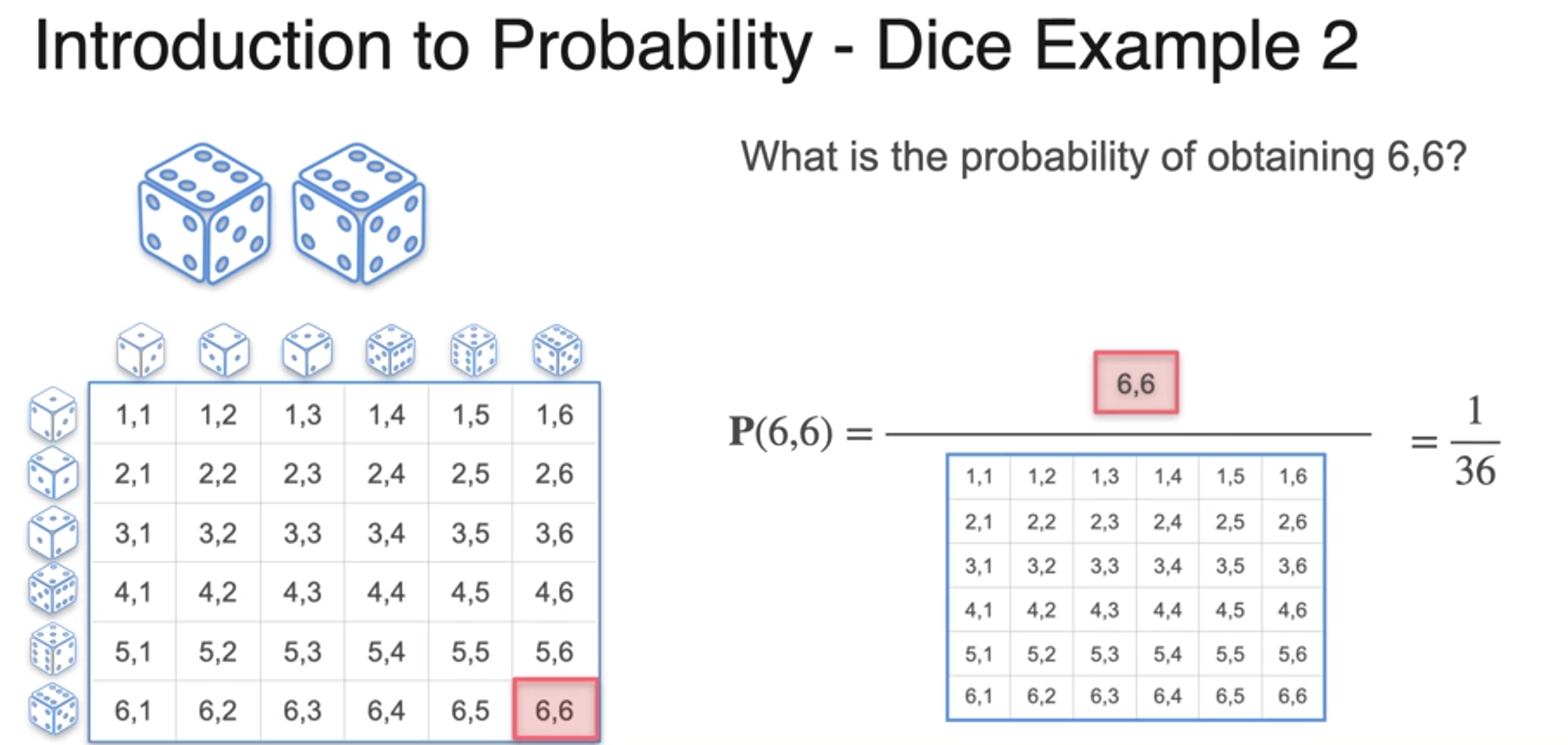
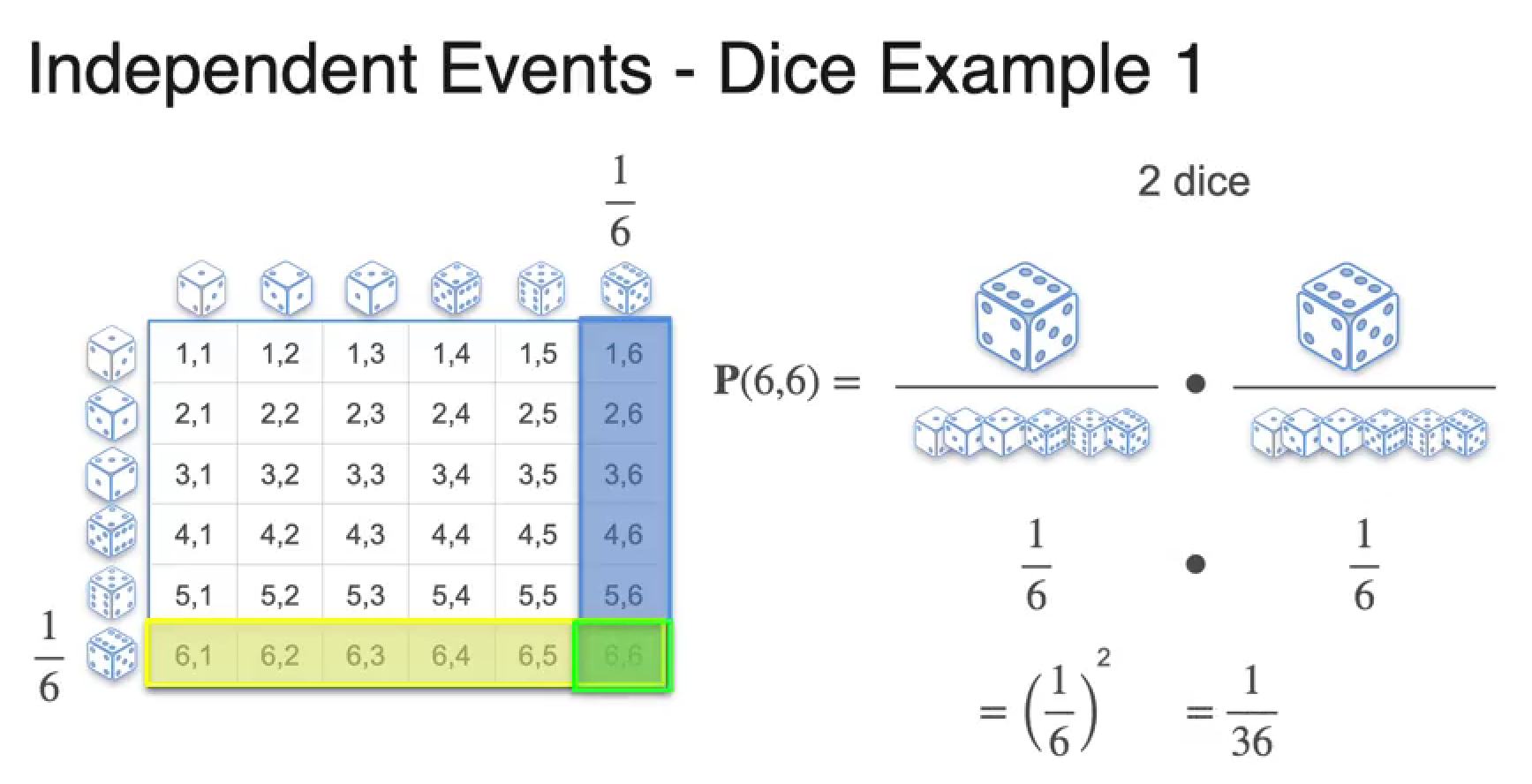
What is Probability? - Dice Example
Complement of Probability


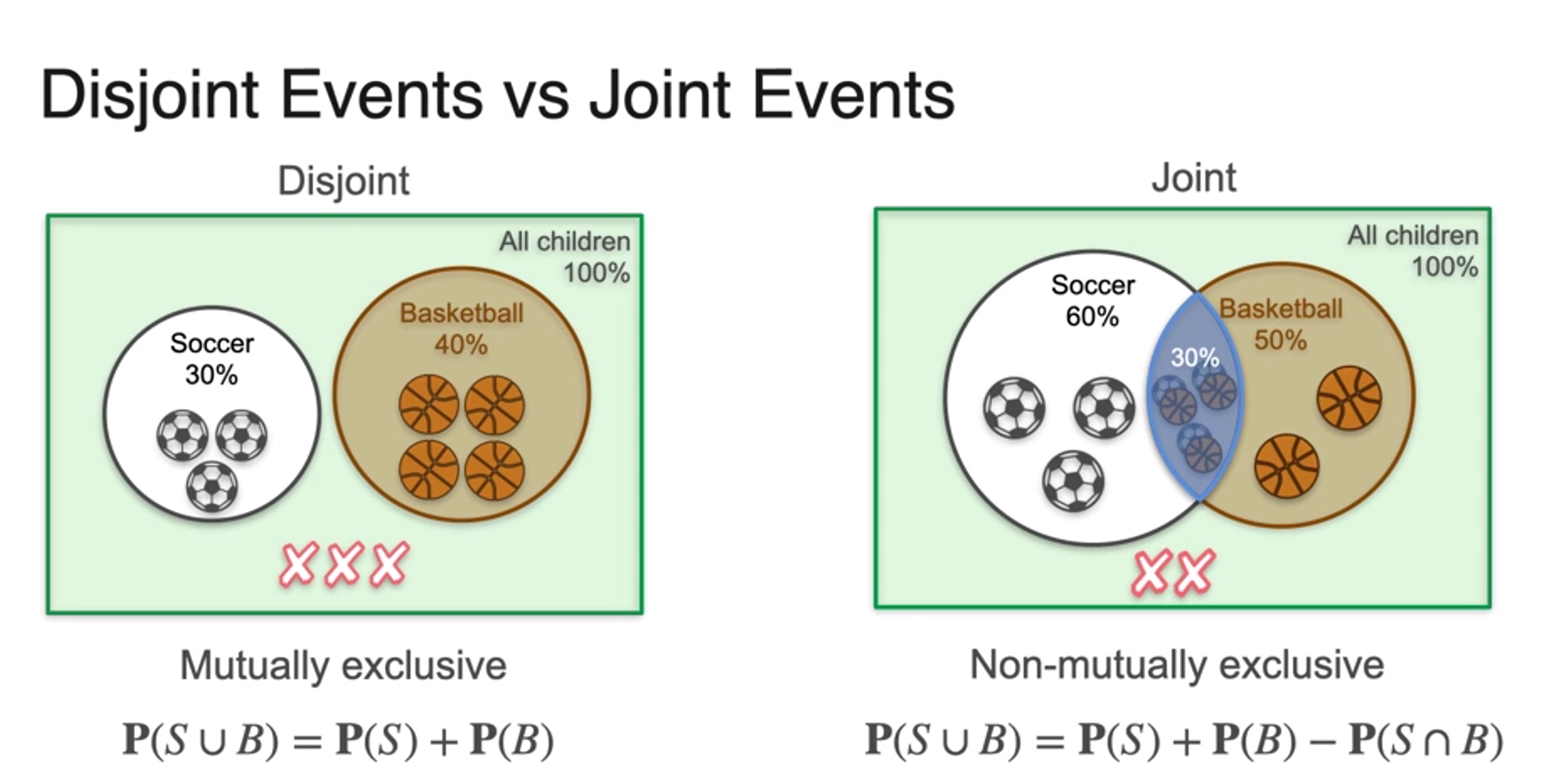
Sum of Probabilities (Disjoint Events)
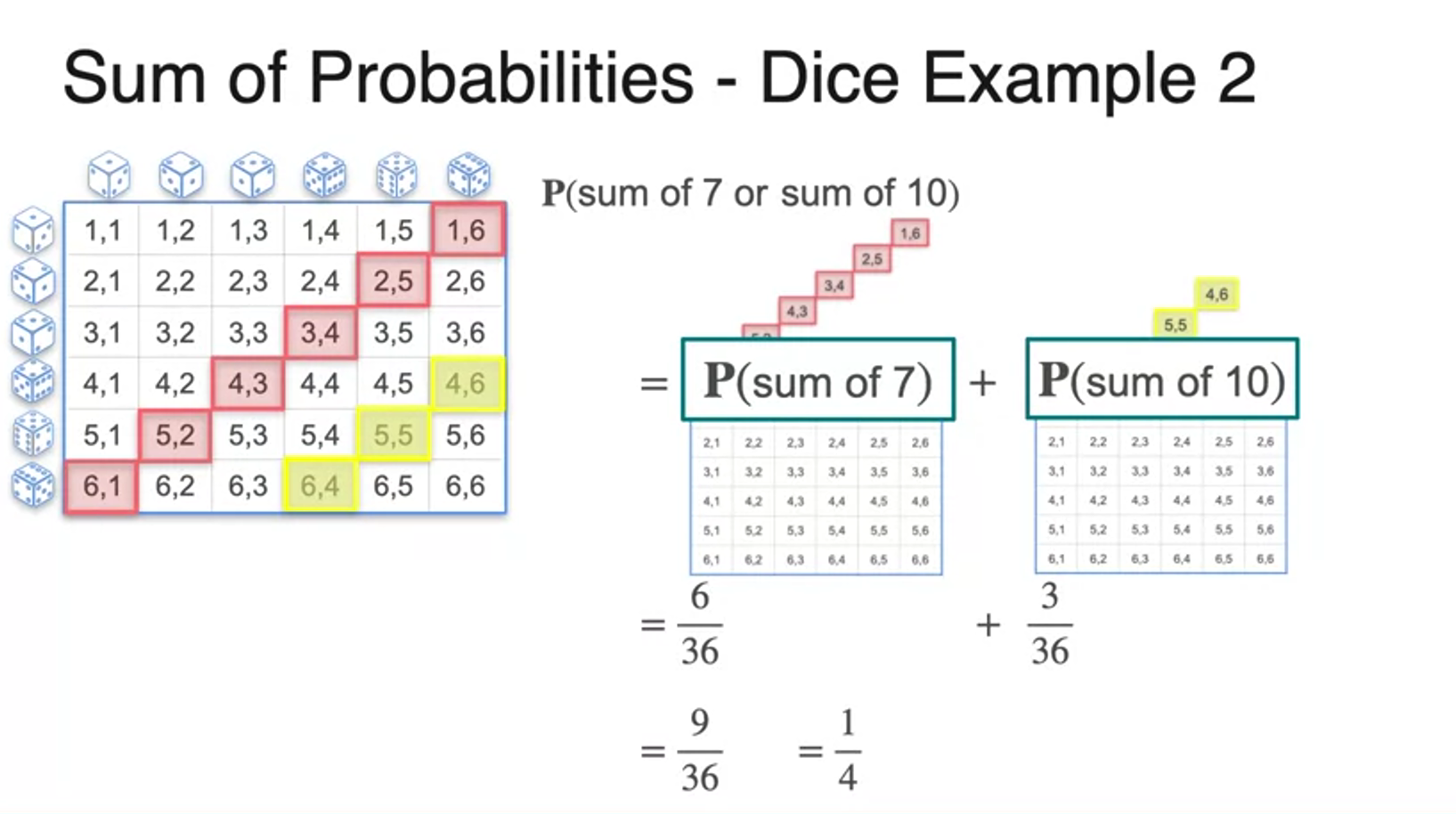
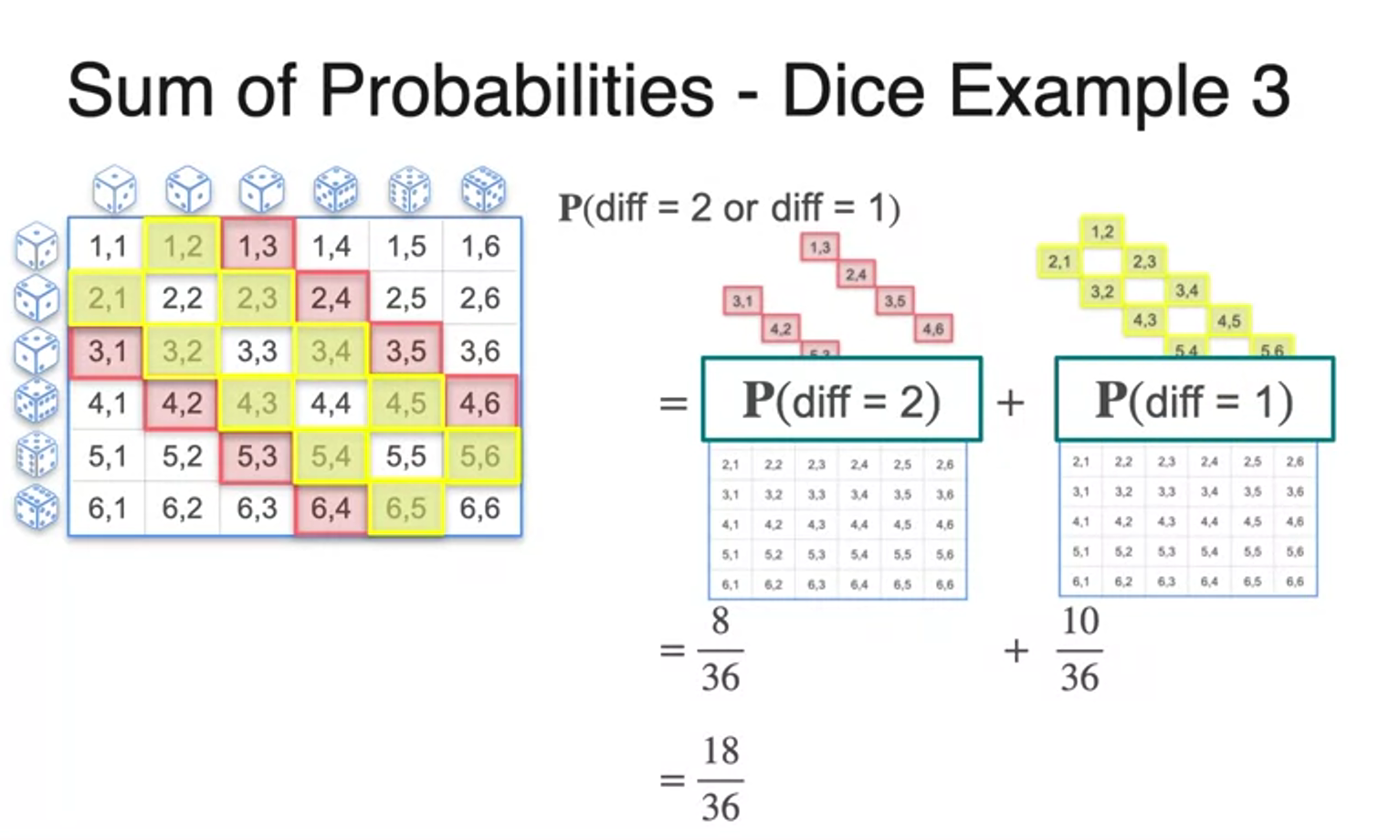
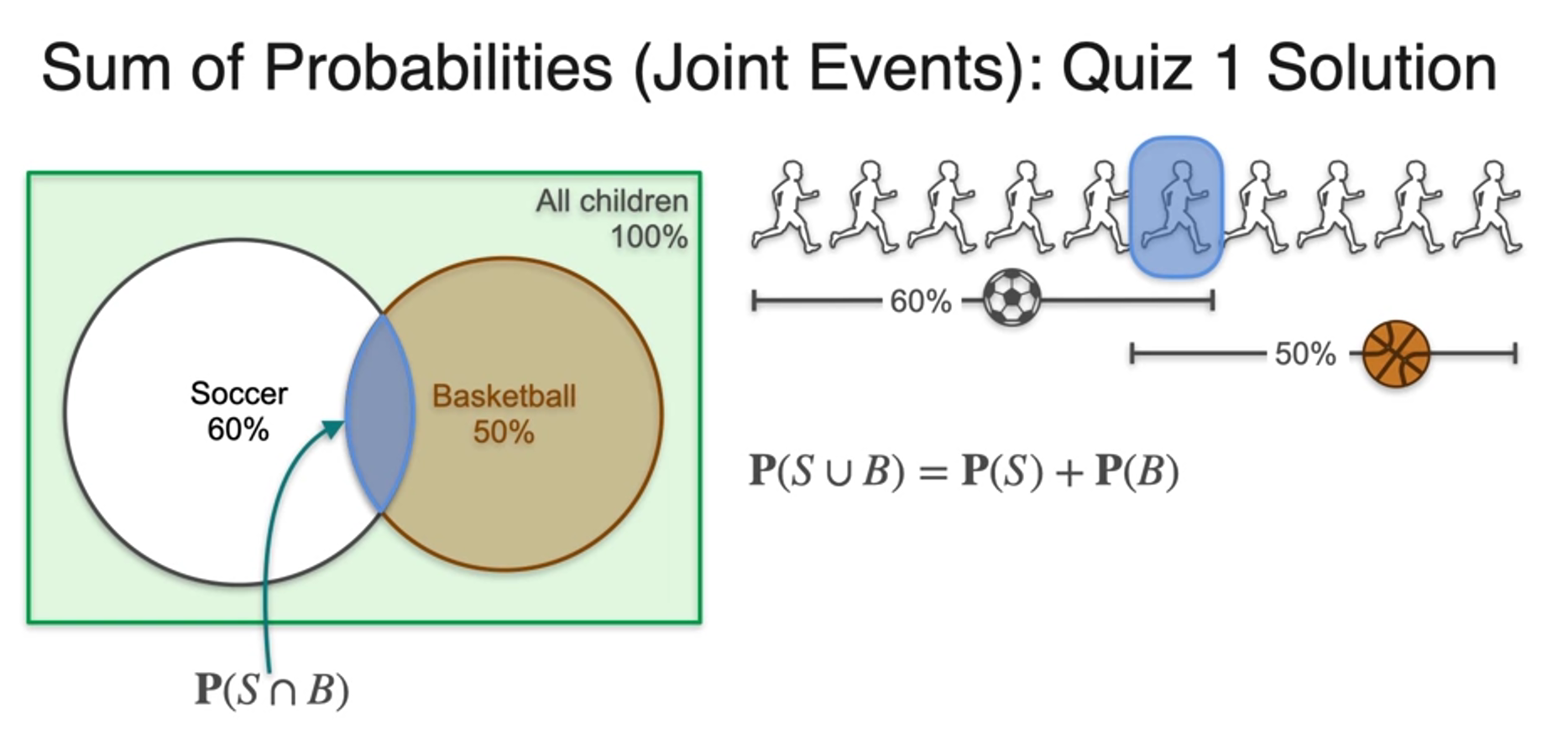
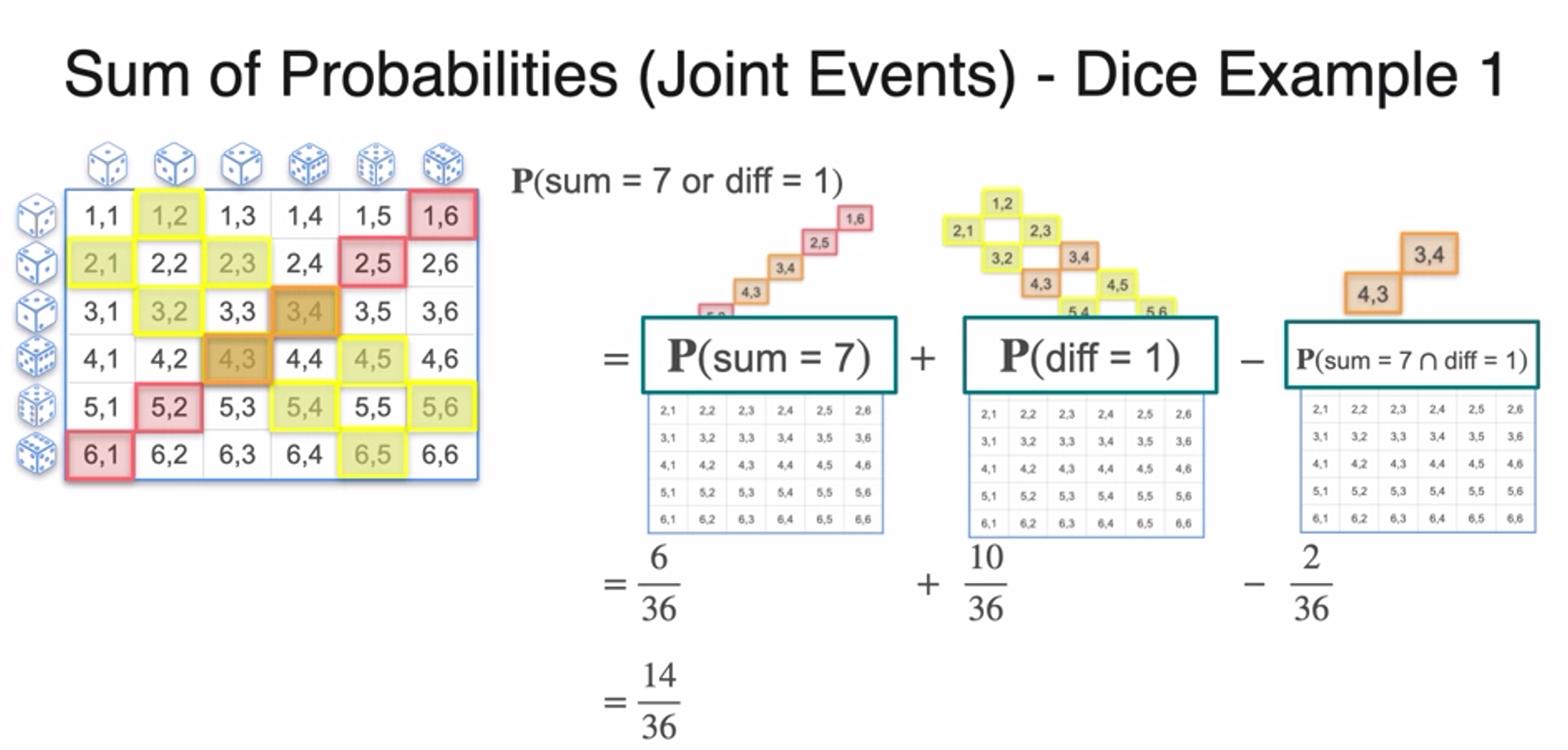
Sum of Probabilities (Joint Events)
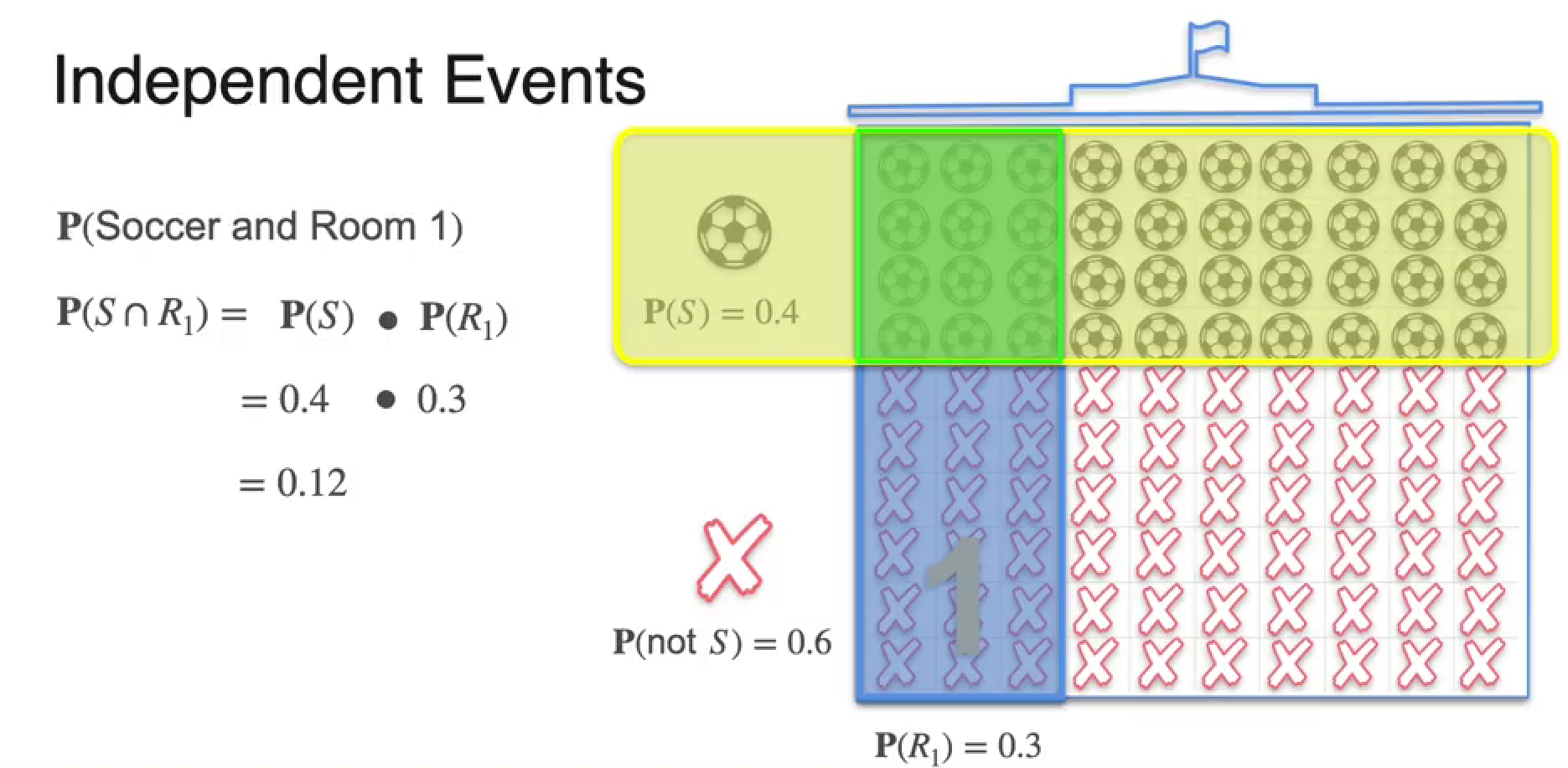
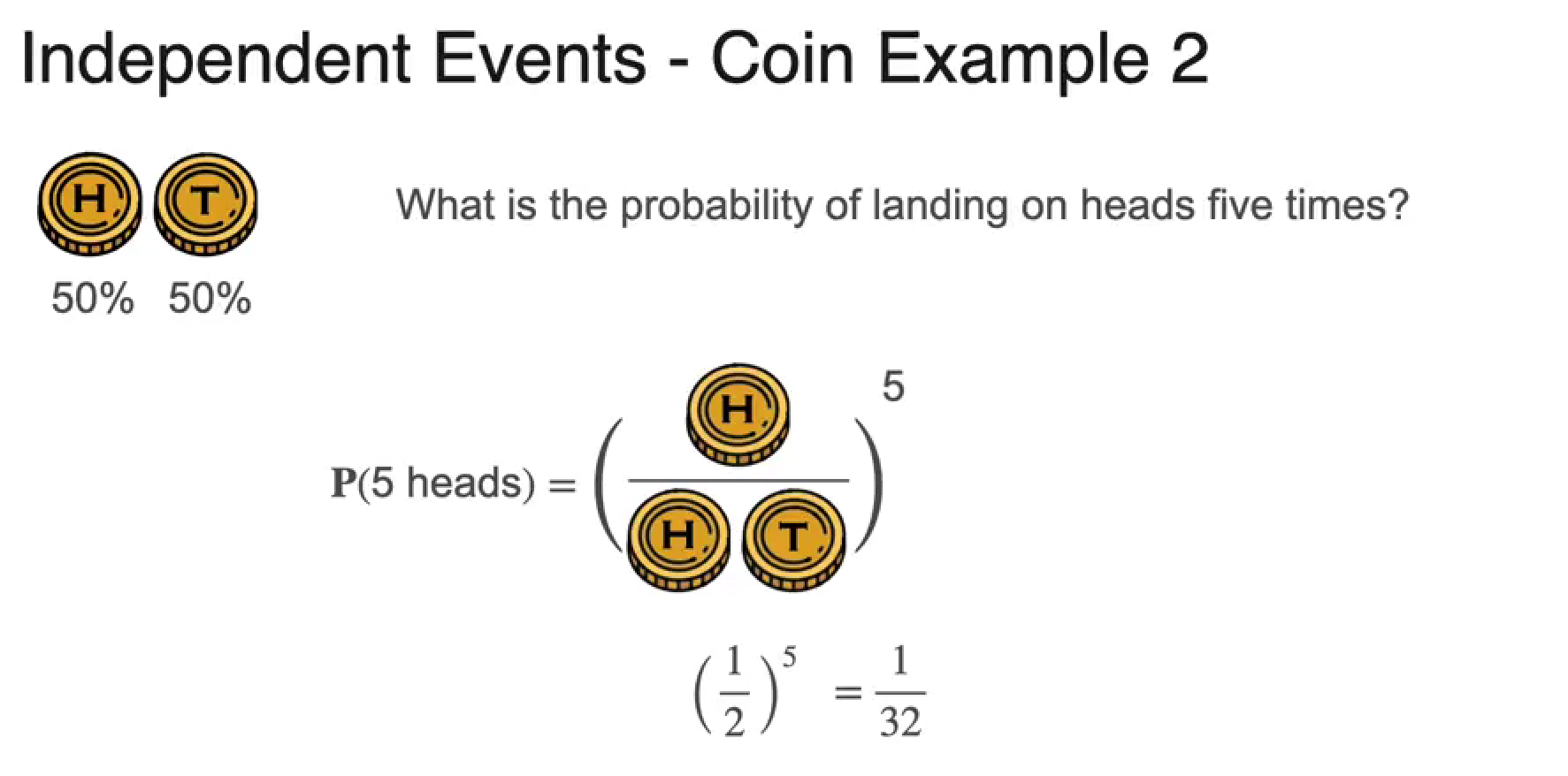
Independence
Birthday problem
- Among 30 people the probability of everyone has different birthday
- 9 people case
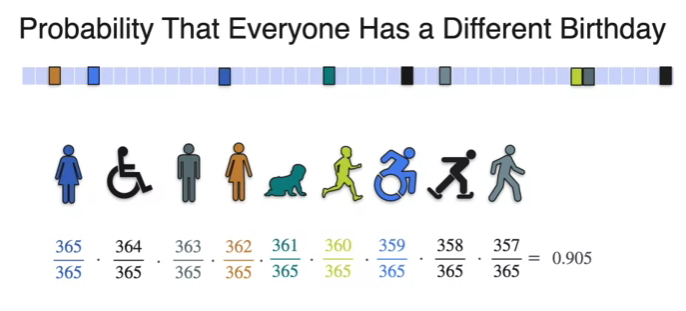
- Drops very steeply
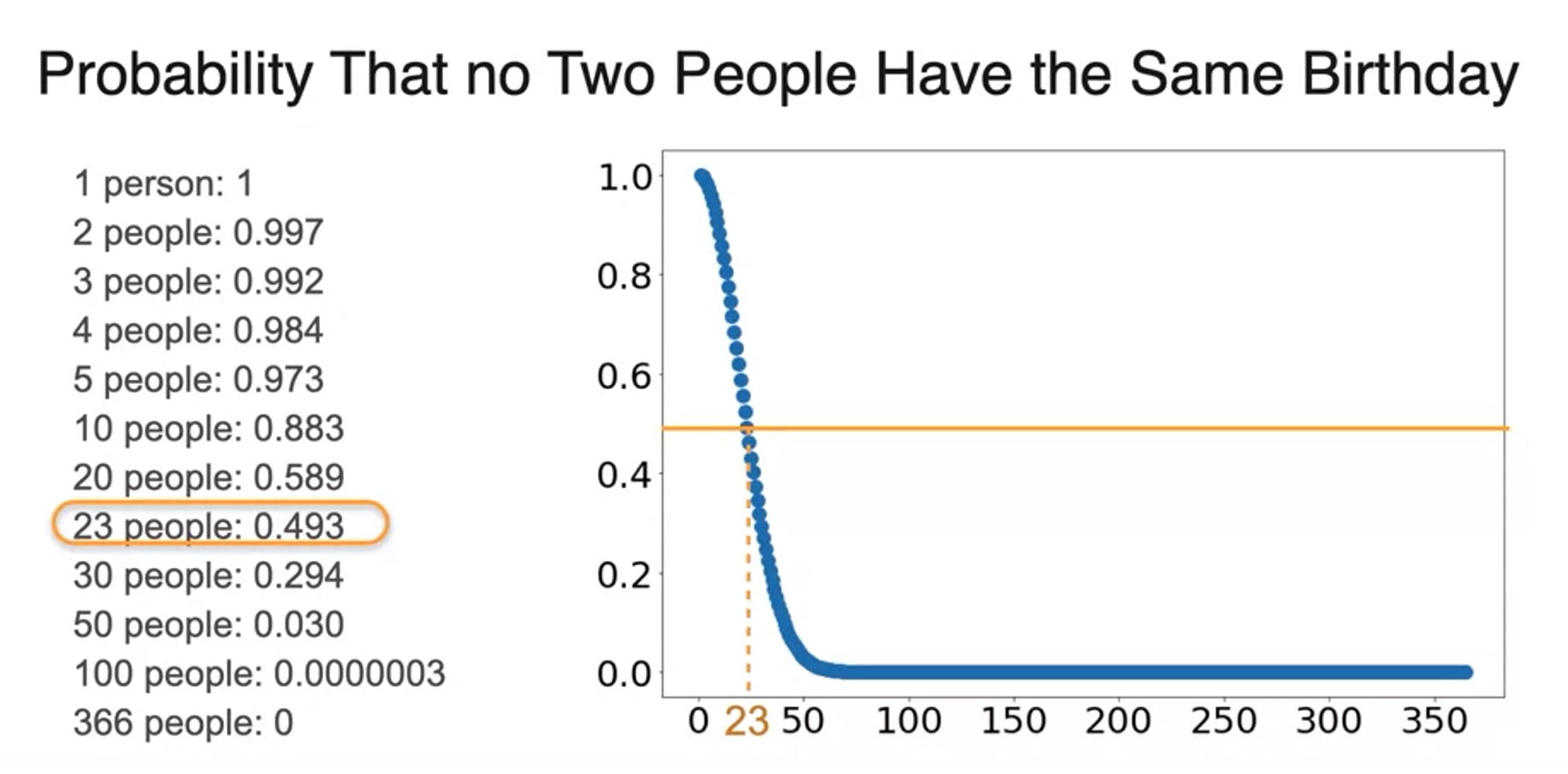
- 9 people case
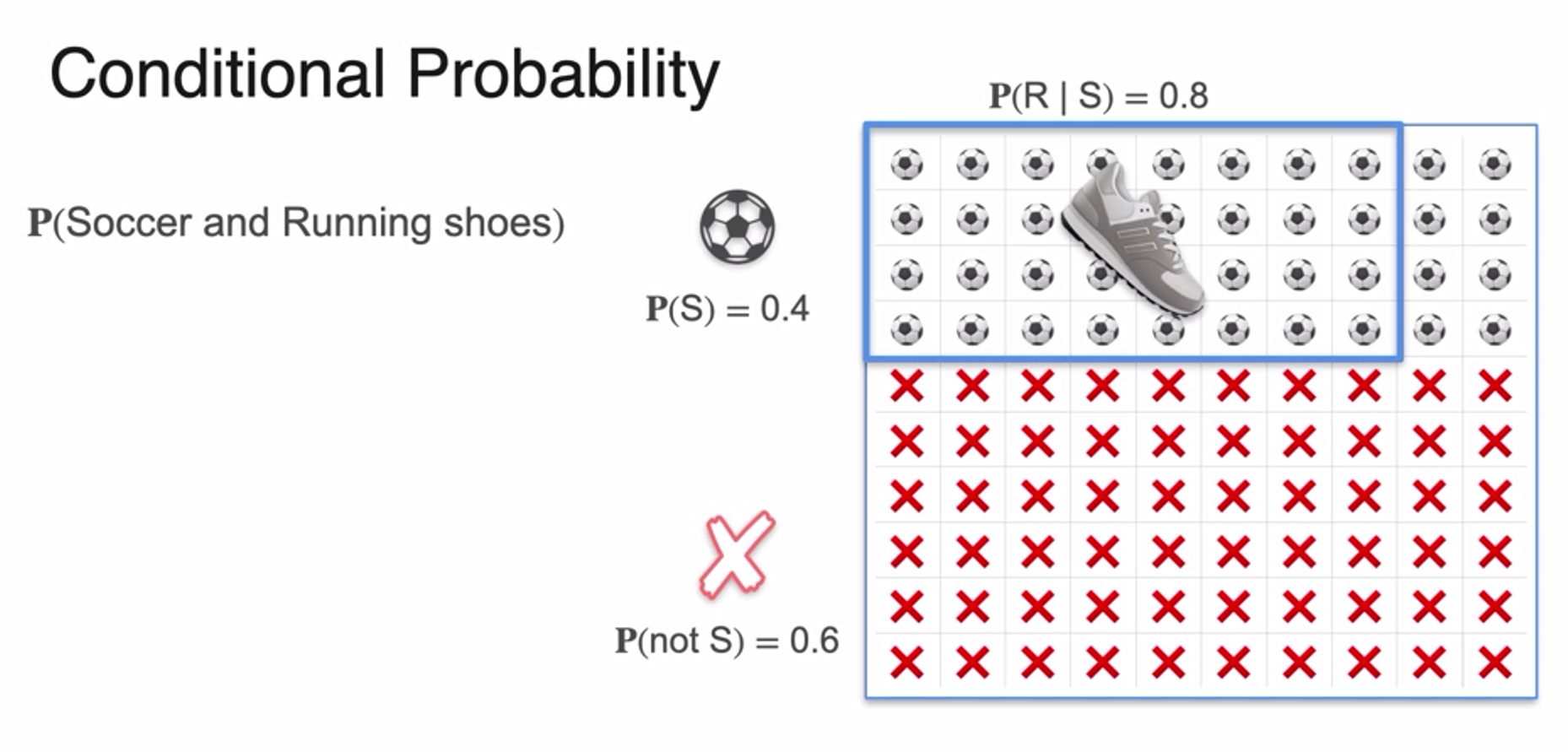
Conditional Probability - Part 1
-
information : The probability that today is humid
- condition : yesterday was raining
probability changes according to the existence of condition


-
-
when and independent
-
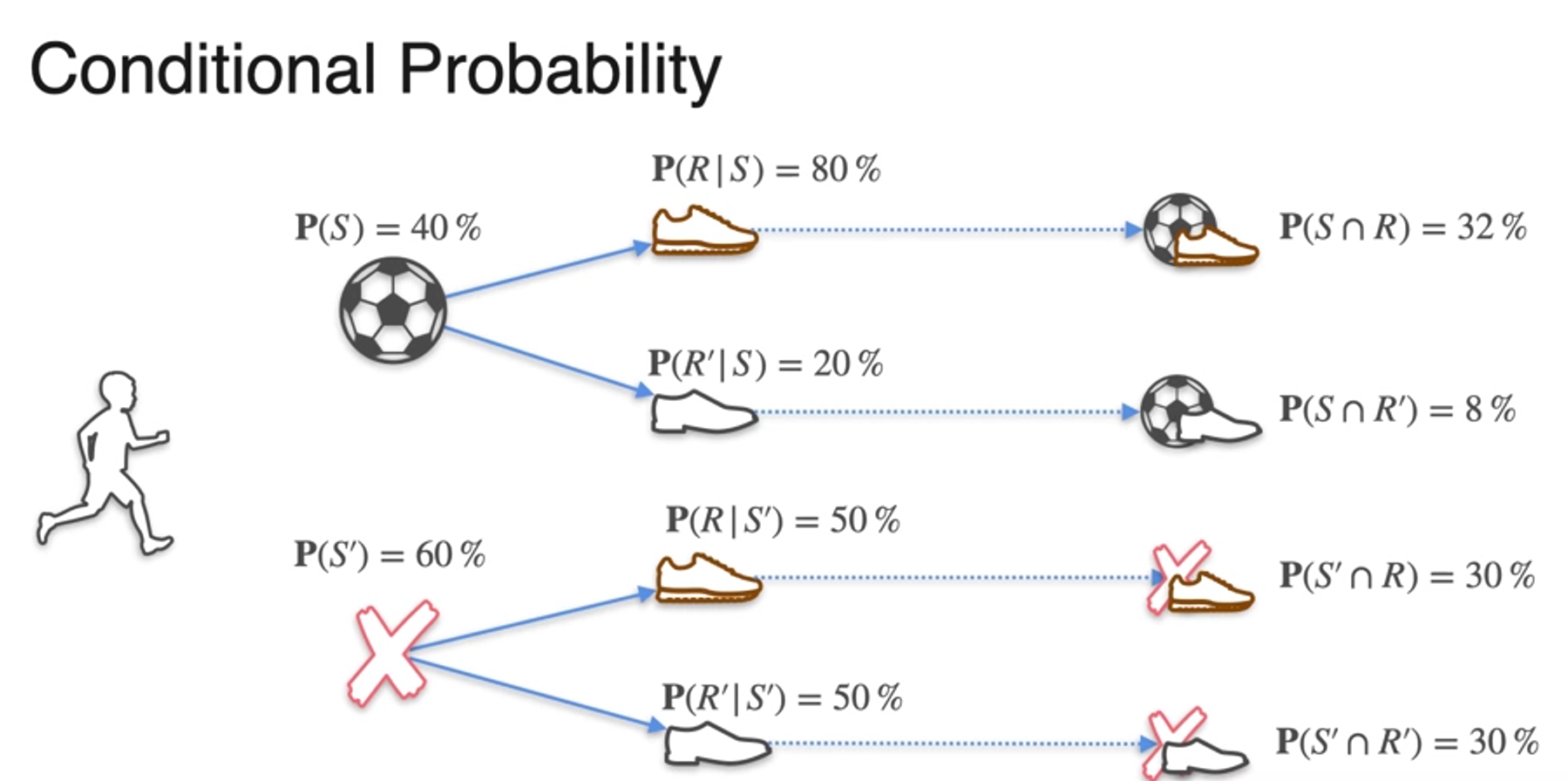
The General Product Rule
- when independent!
-


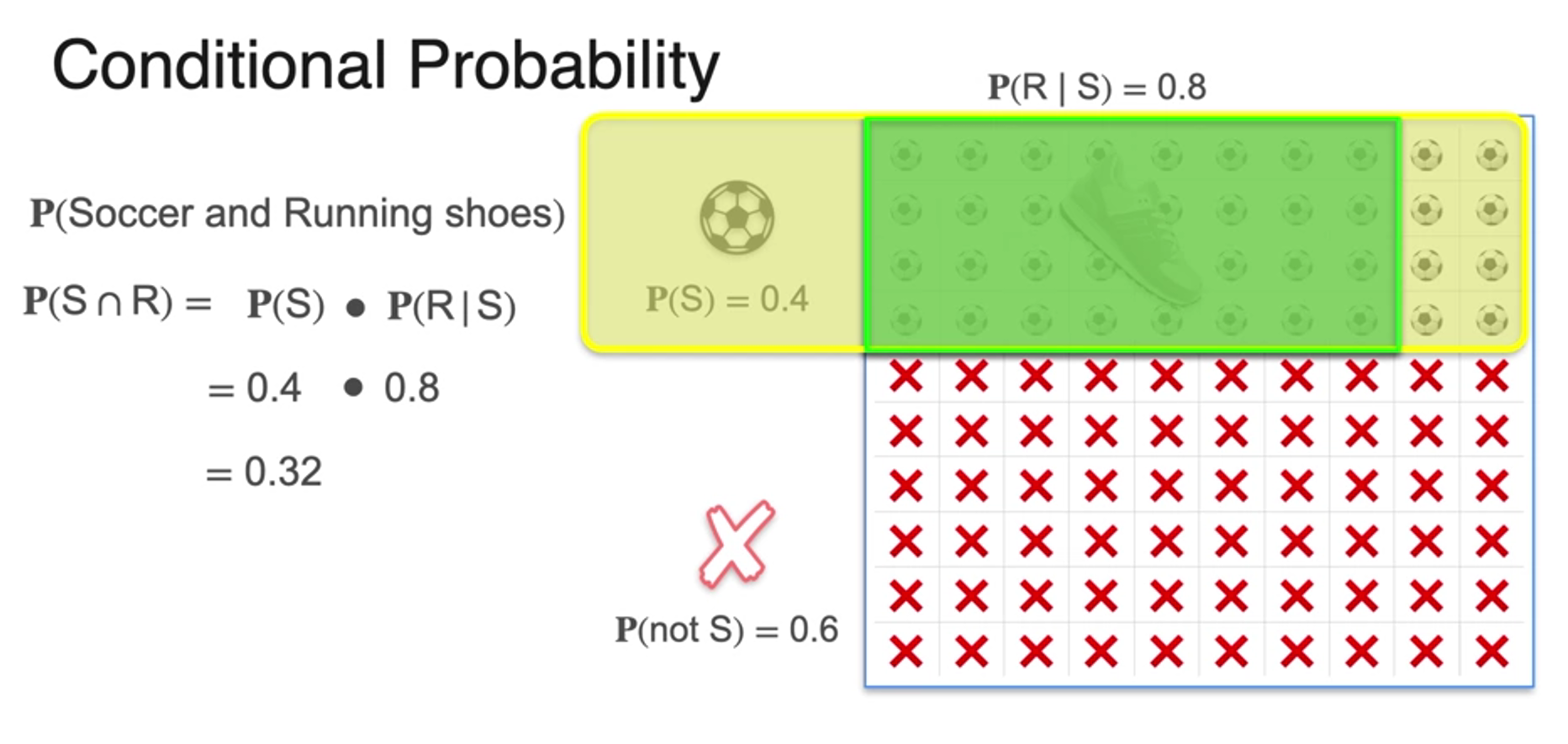
Conditional Probability - Part 2
= 0.4 0.8
= 0.32
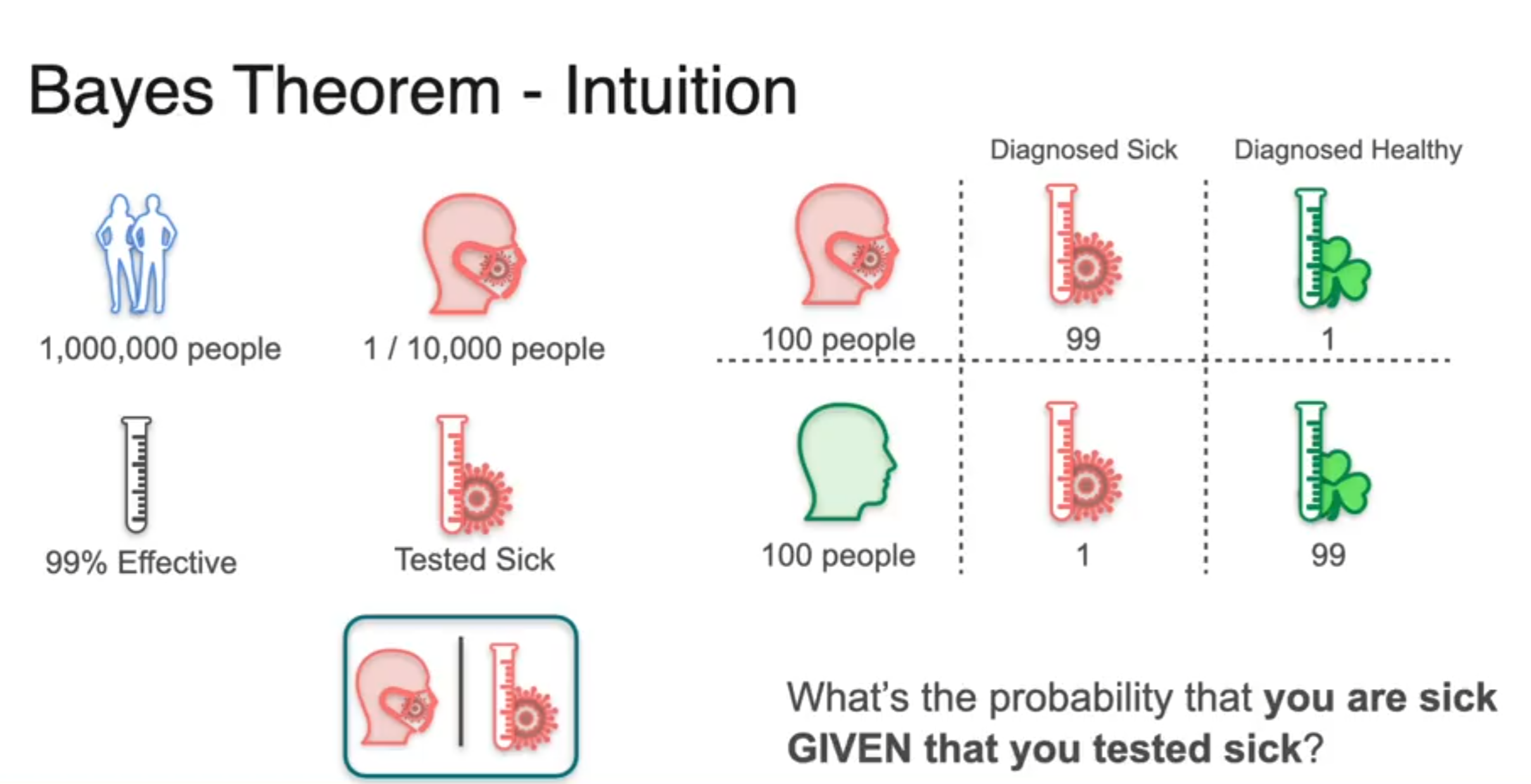
Bayes Theorem - Intuition
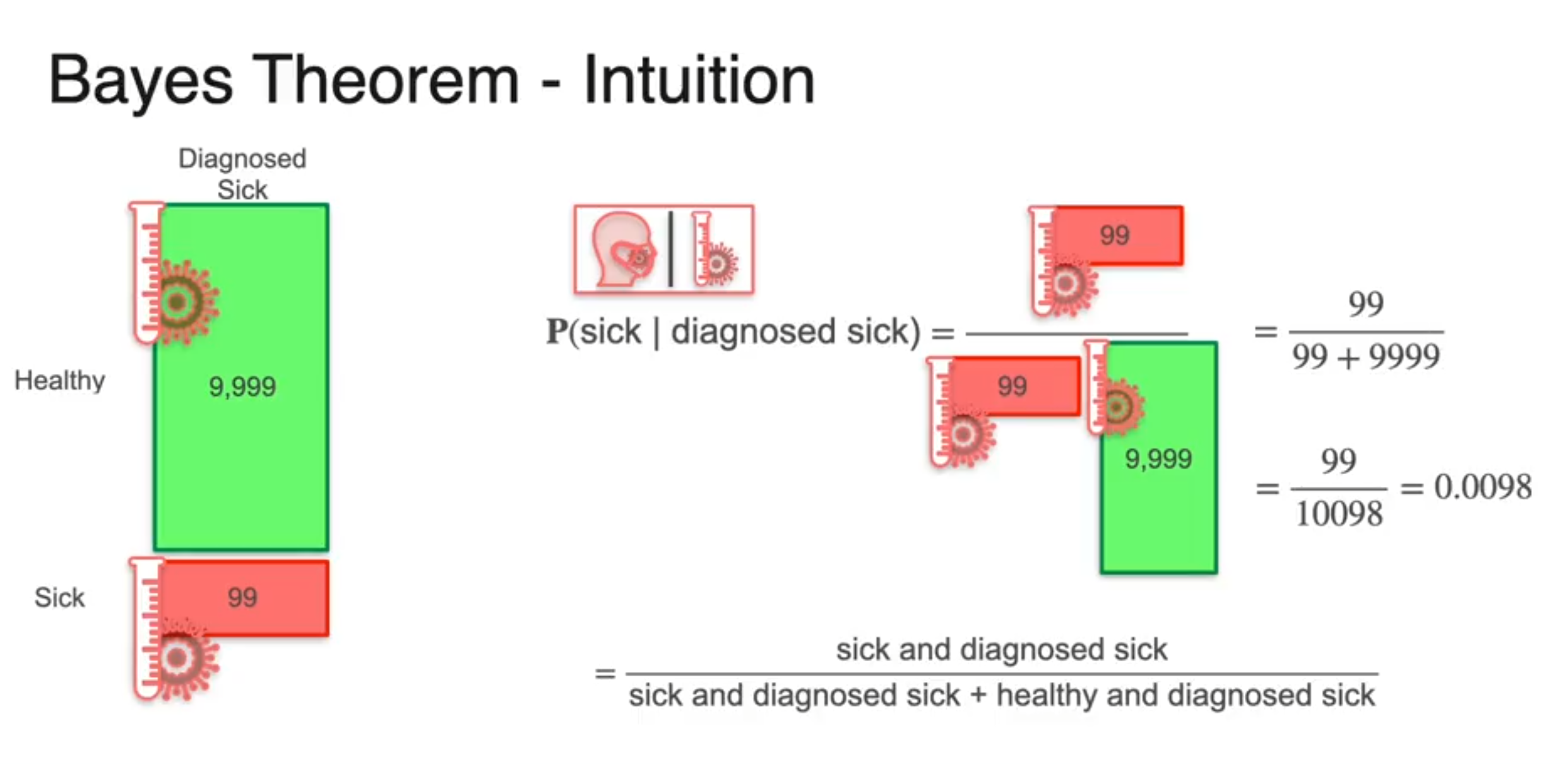
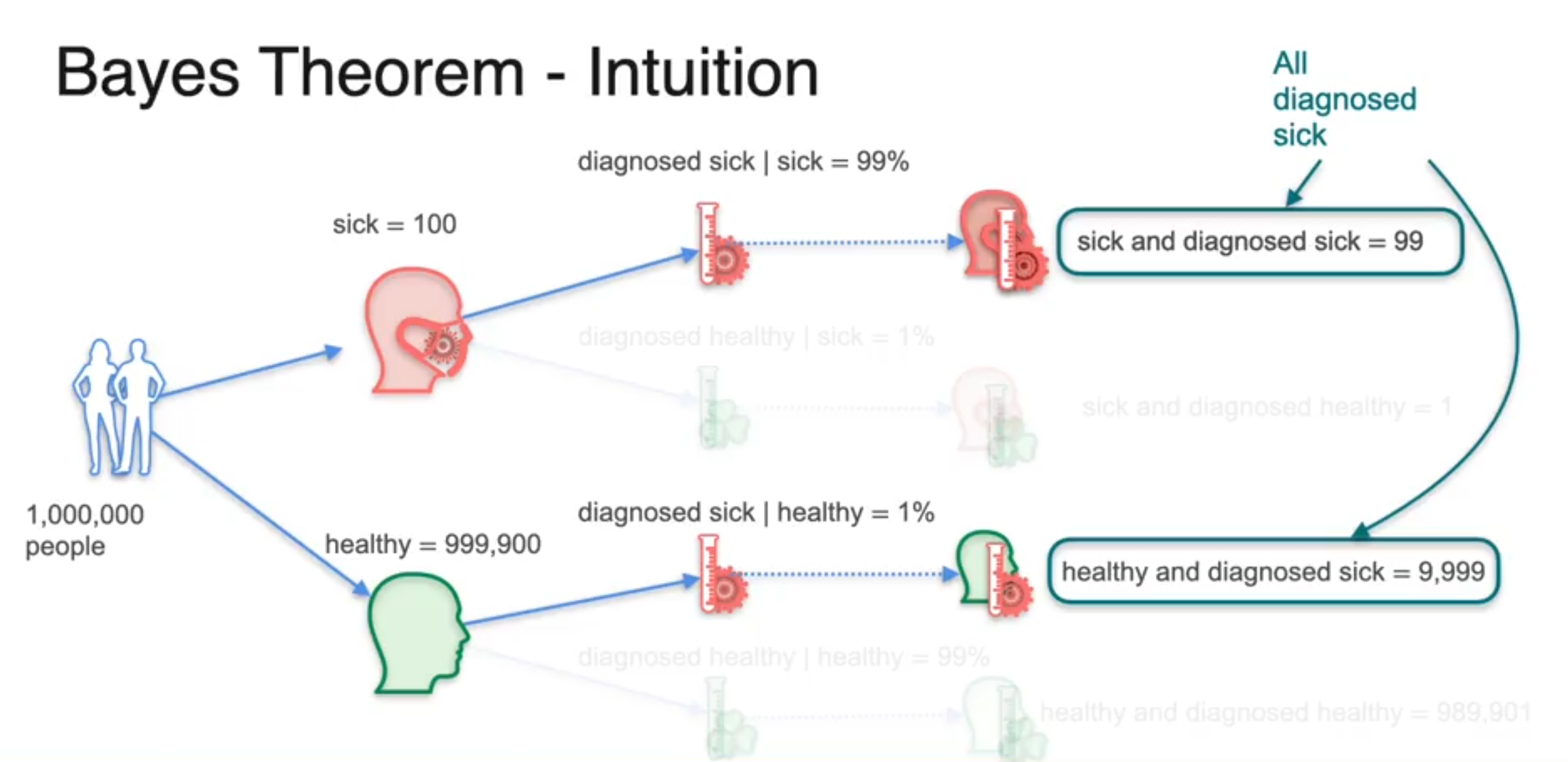

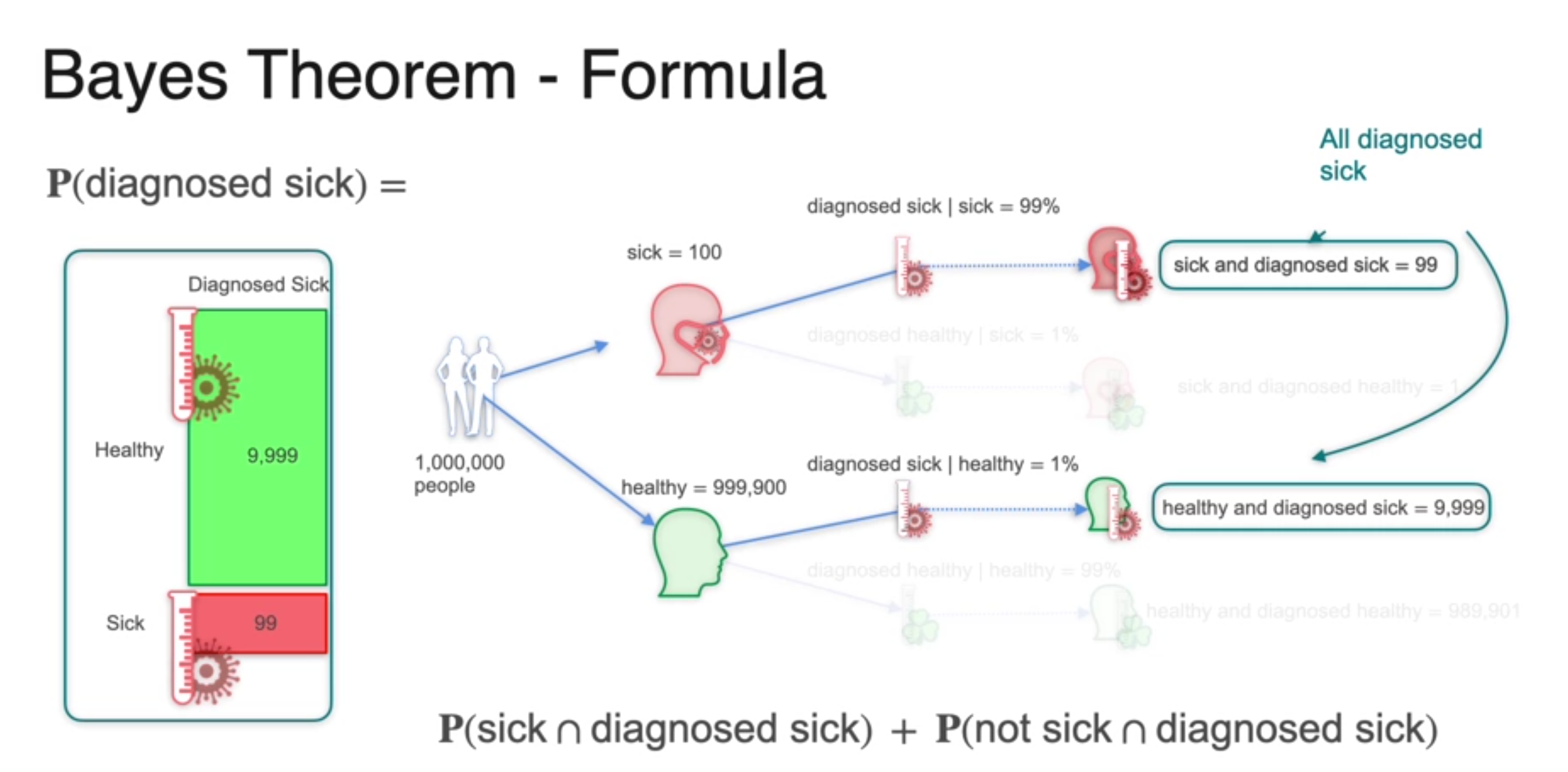
Bayes Theorem - Mathematical Formula



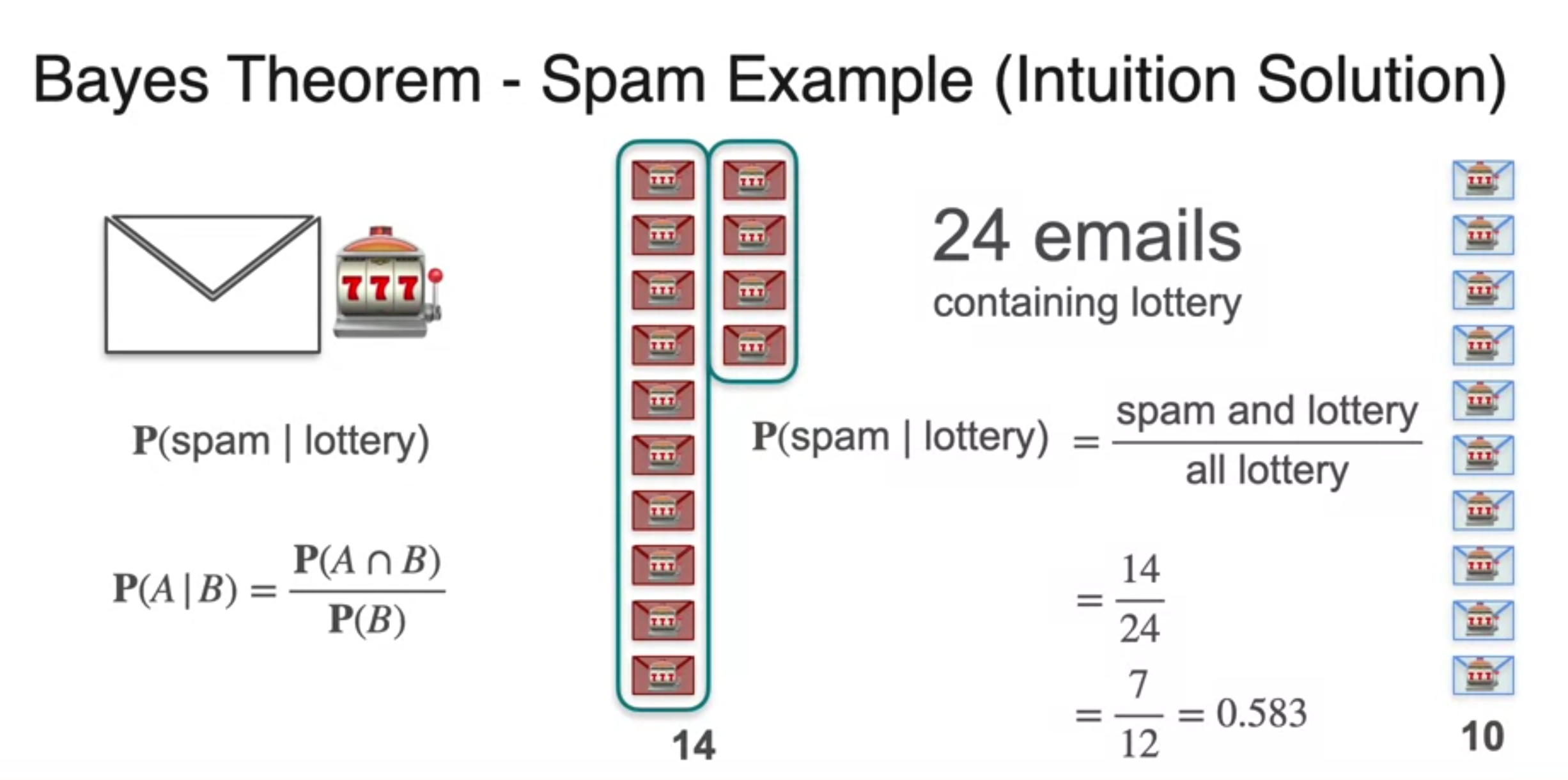
Bayes Theorem - Spam example



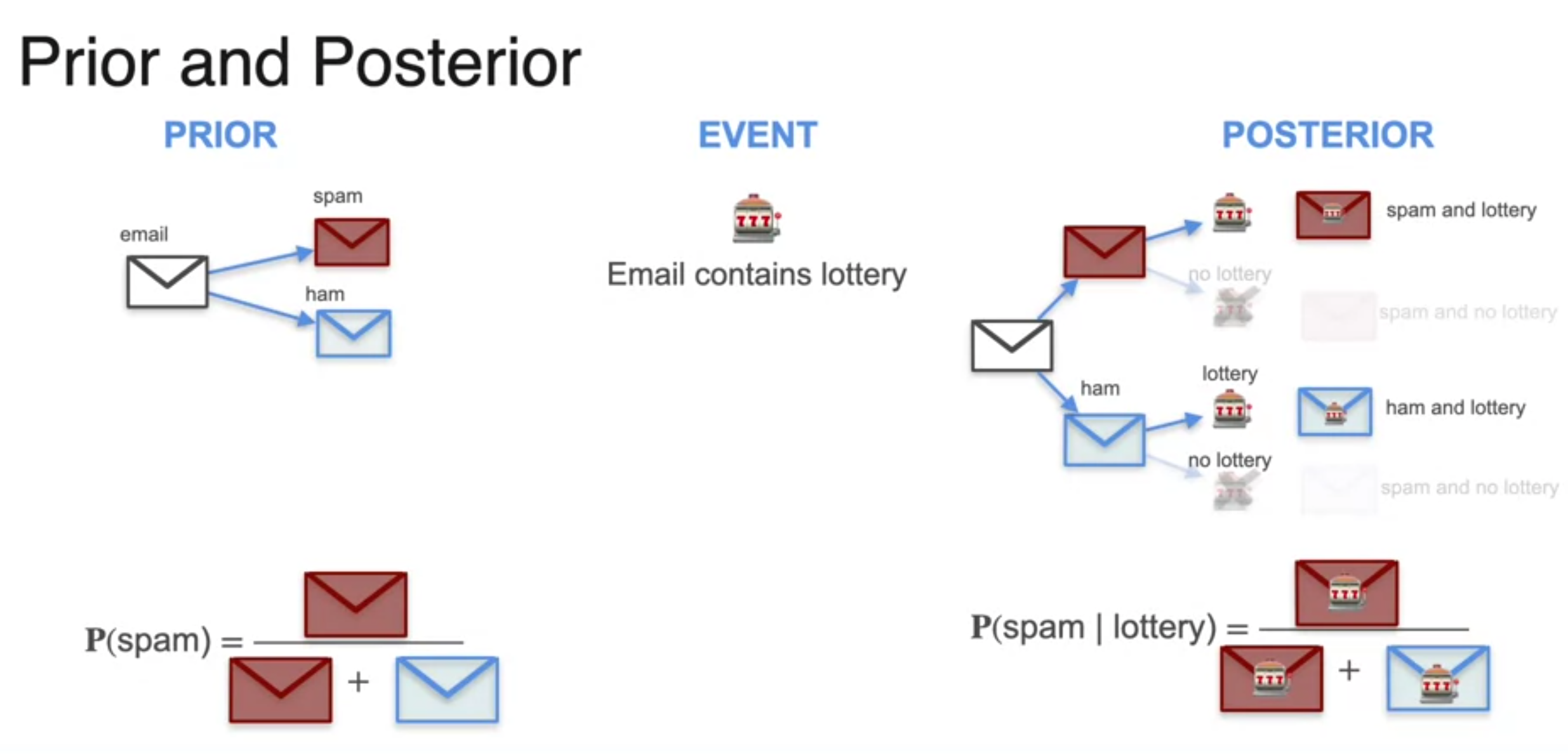
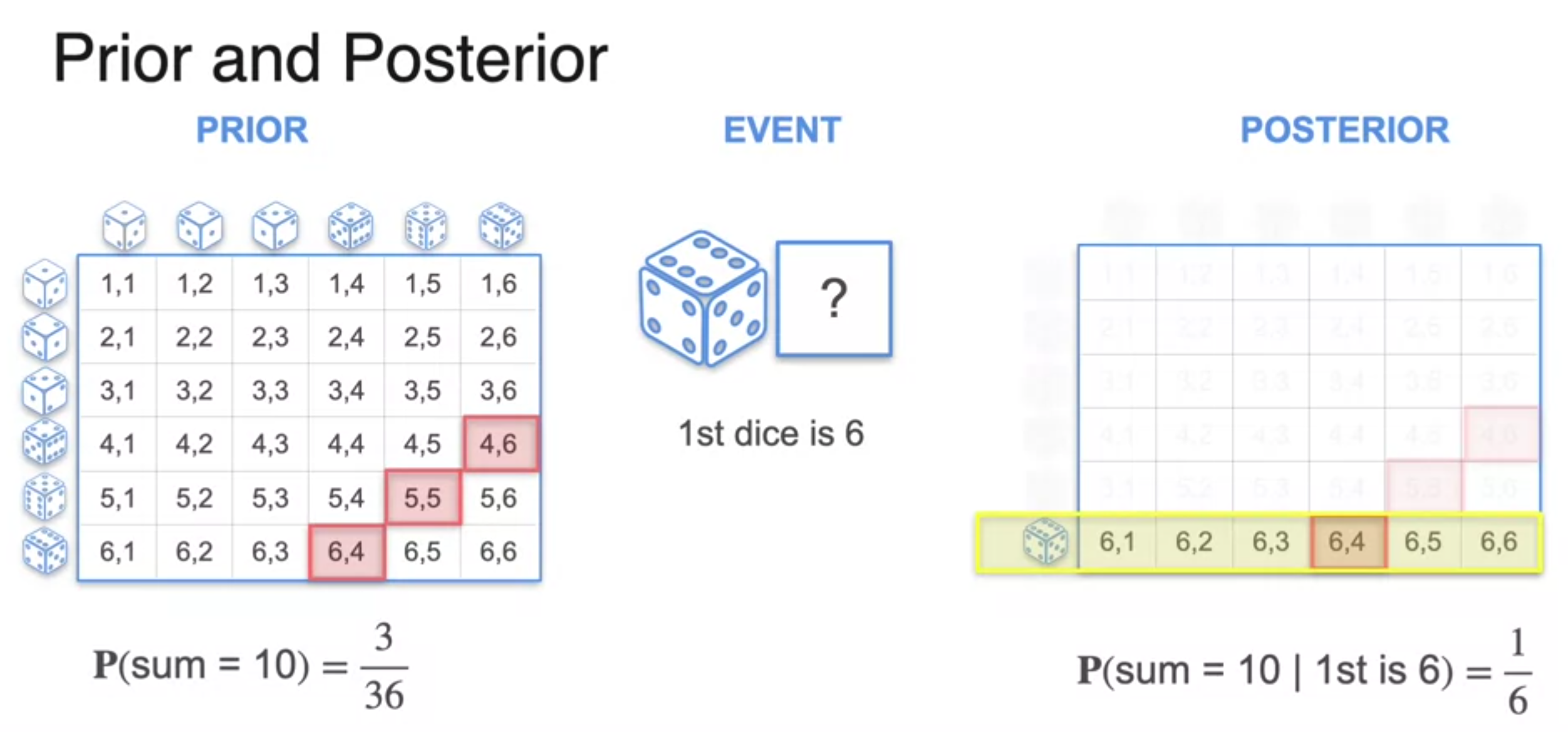
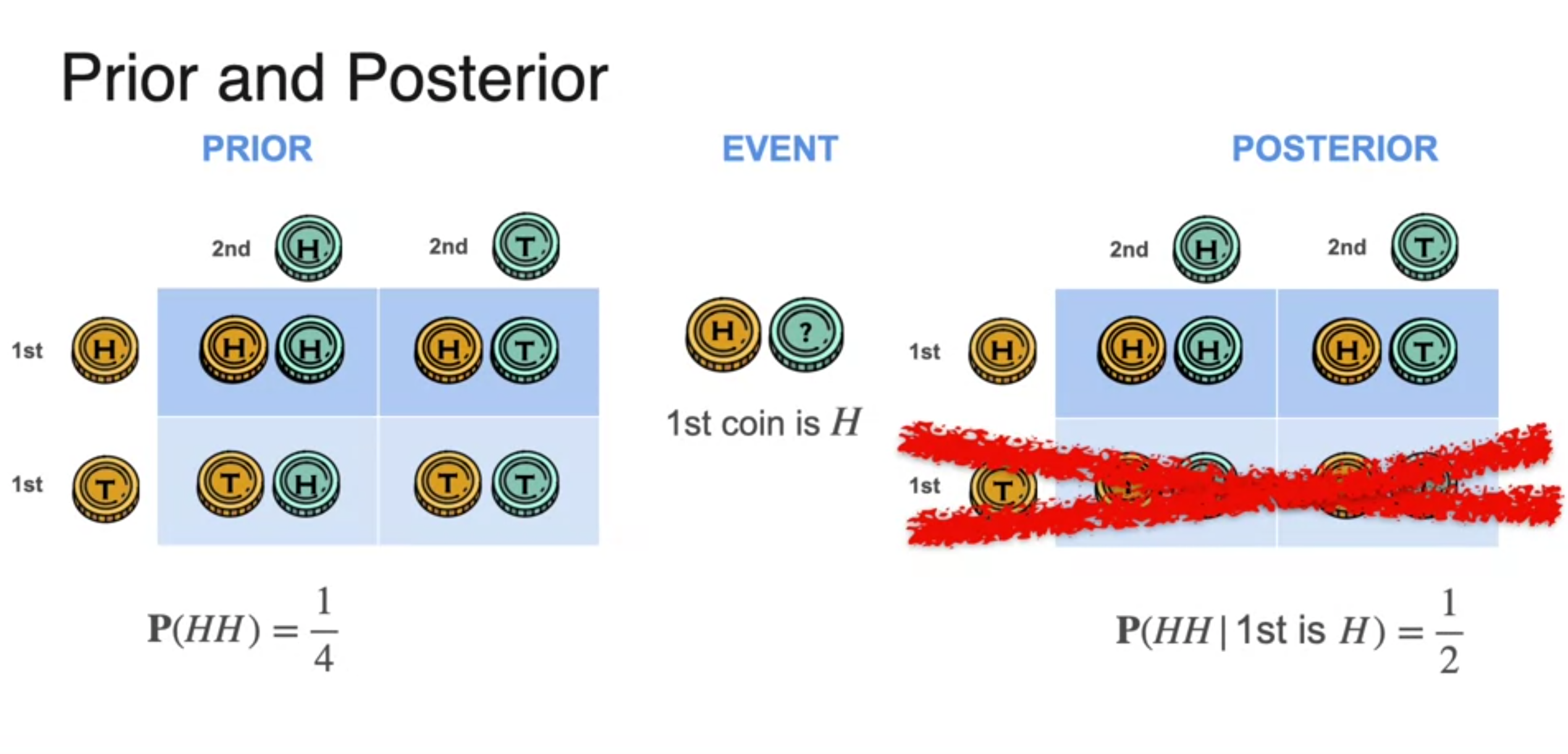
Bayes Theorem - Prior and Posterior
-
PRIOR : original probability, P(A)
-
EVENT : gives information about the probability, P(E)
-
POSTERIOR : with them can calculate P(A/E)
- always better estimation than the prior
Bayes Theorem - The Naive Bayes Model




Probability in Machine Learning
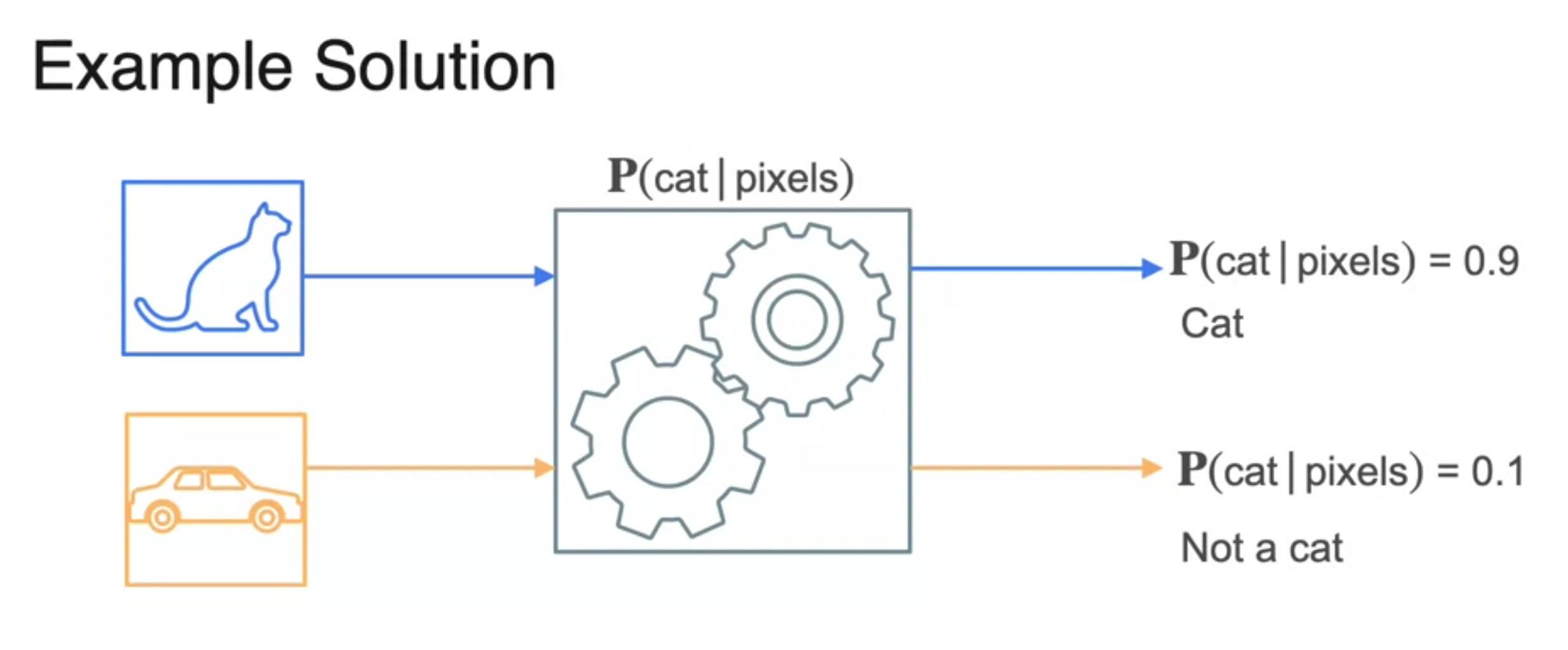

Lesson 2 - Probability Distribution
Random Variables

- Discrete random variables(이산확률변수)
- Continuous random variables(연속확률변수)

Probability Distributions (Discrete)
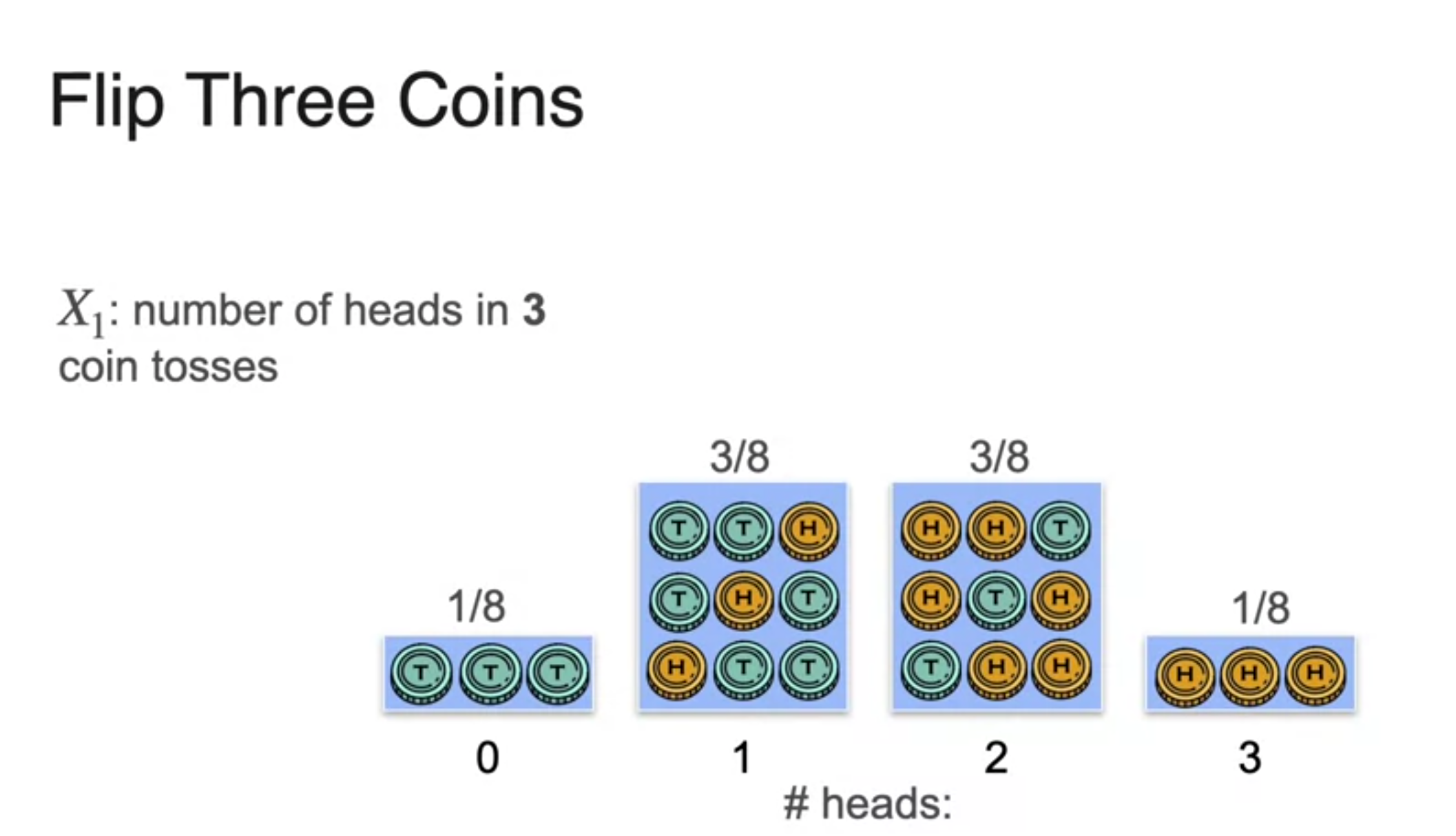
-
1개 확률
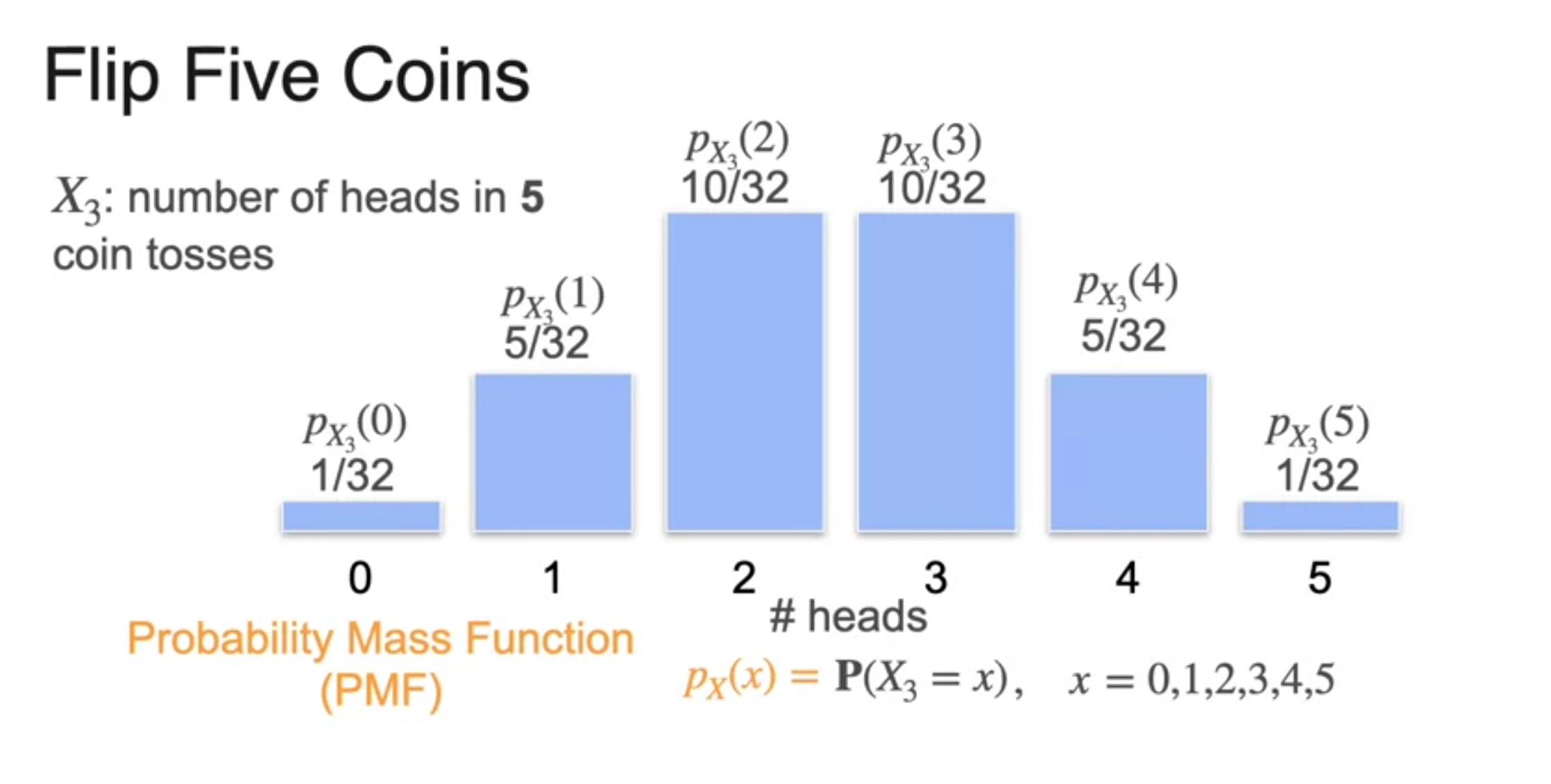
-
Probability Mass Function(확률 질량 함수)
- 모든 이산확률 변수는 PMF로 모델링 가능
- PMF의 조건
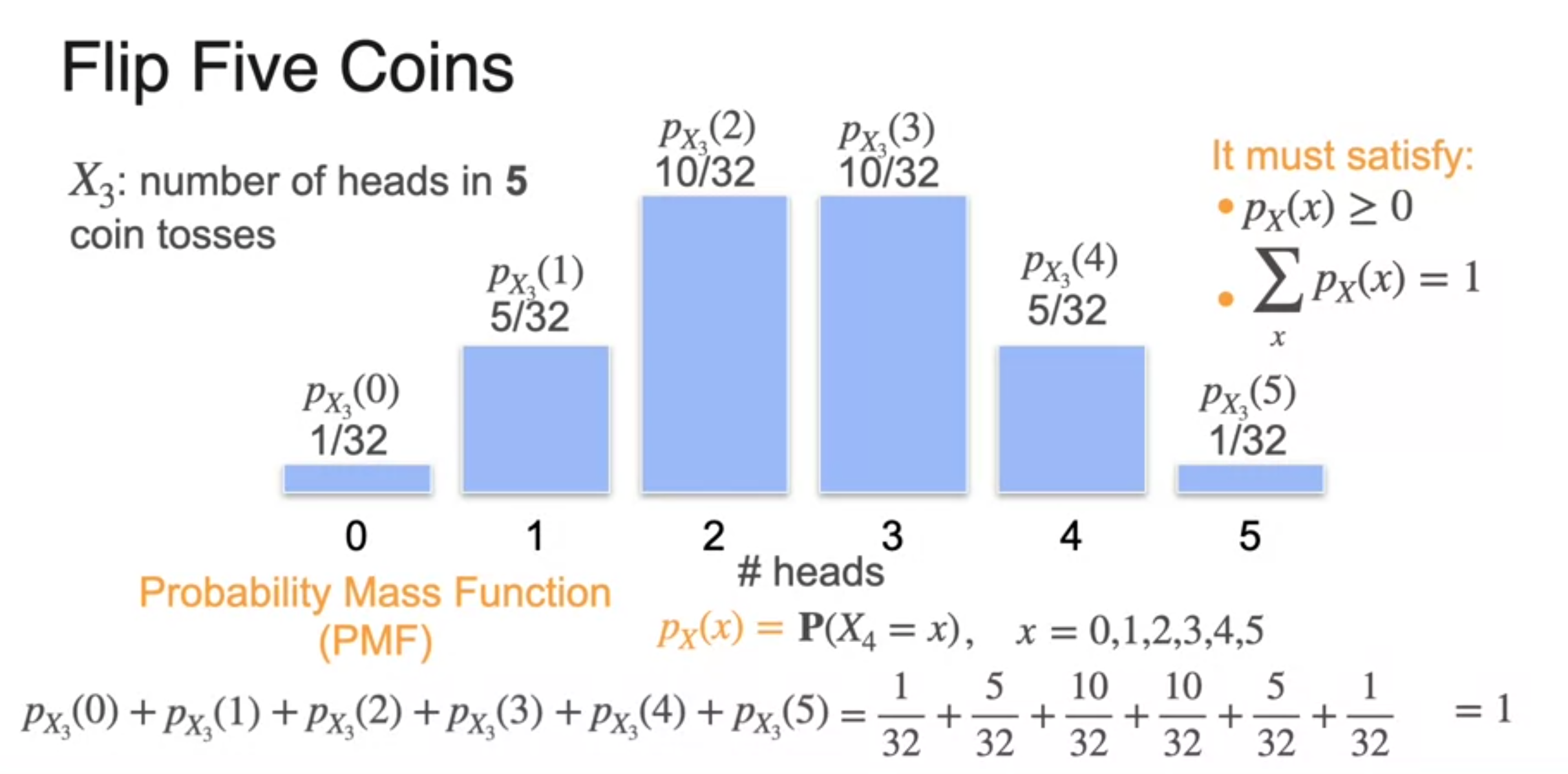
- 모든 랜덤 변수를 나타내는 단이 모델?
- Binomial distribution(이항 분포)
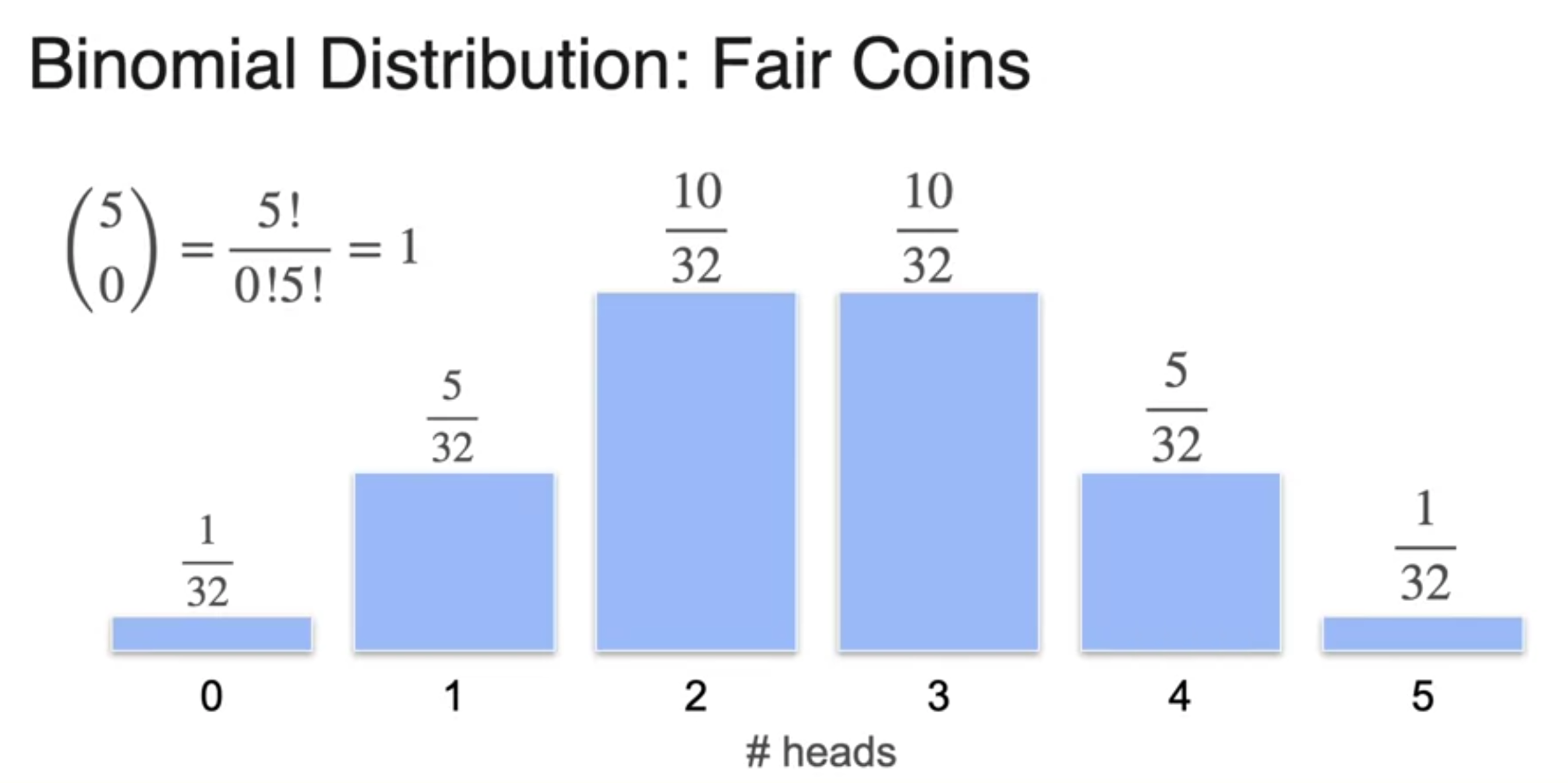
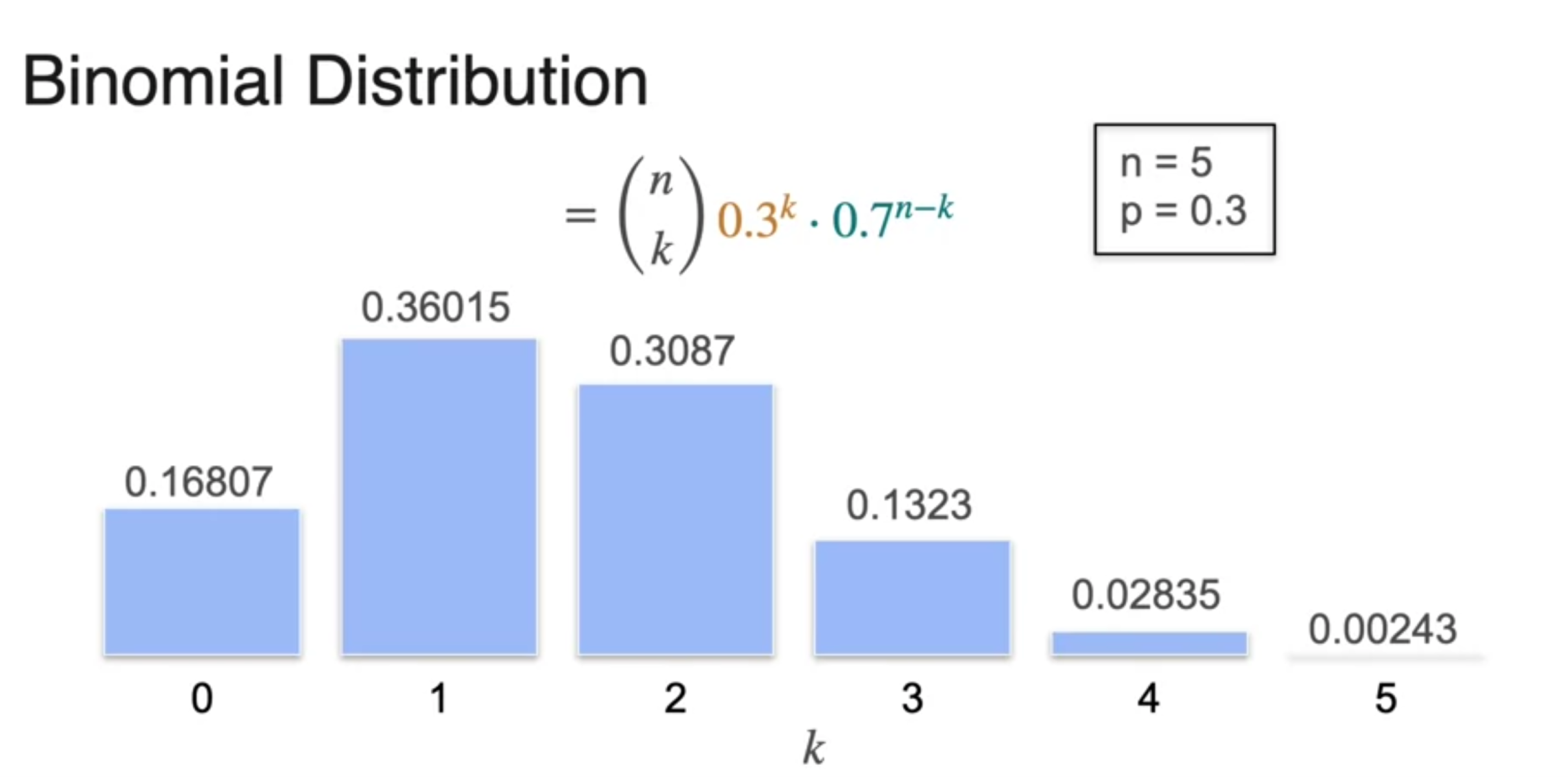
Binomial Distribution

- why PMF has symmetrical shape


- Binomial distribution 수식의 n, p를 파라미터로 본다
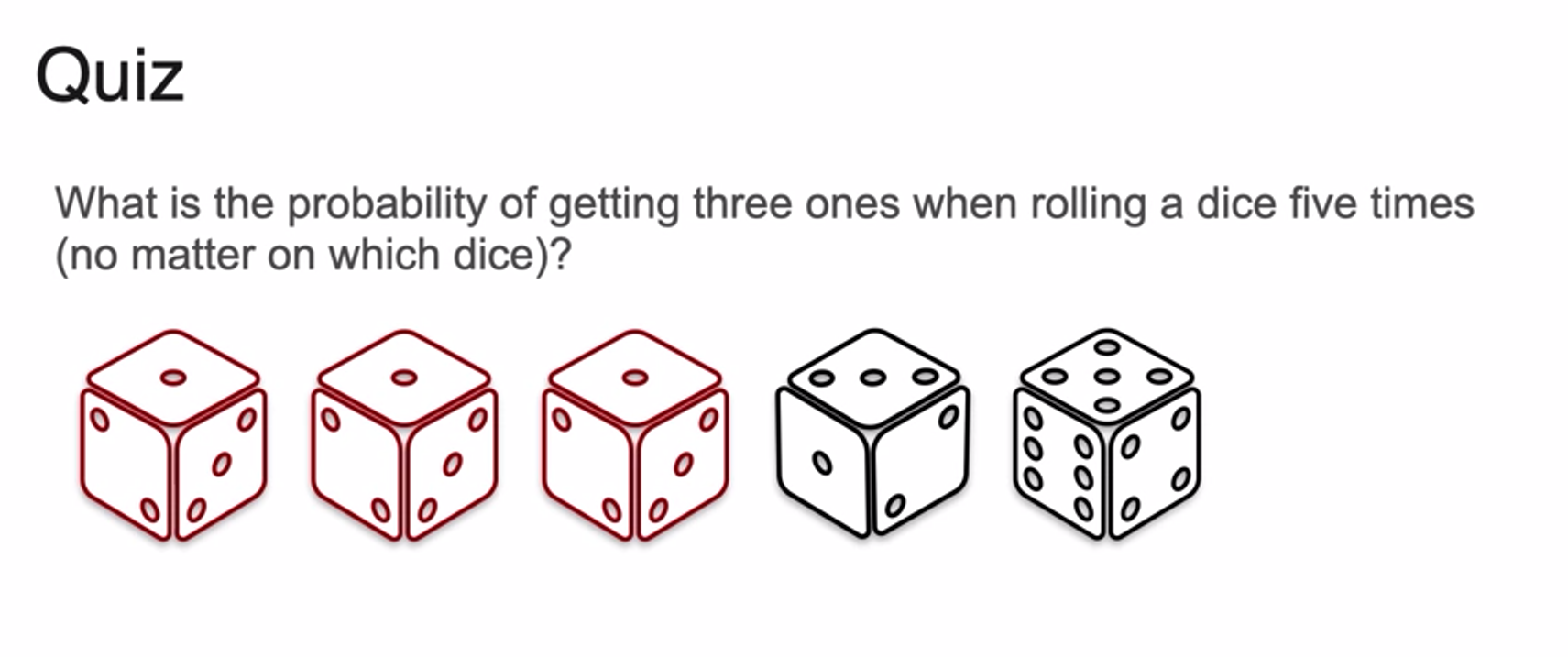
-
answer is
-
이항분포와 베르누이분포
- 시행횟수의 차이다
- 베르누이 분포는 이항분포의 특수한 경우이다
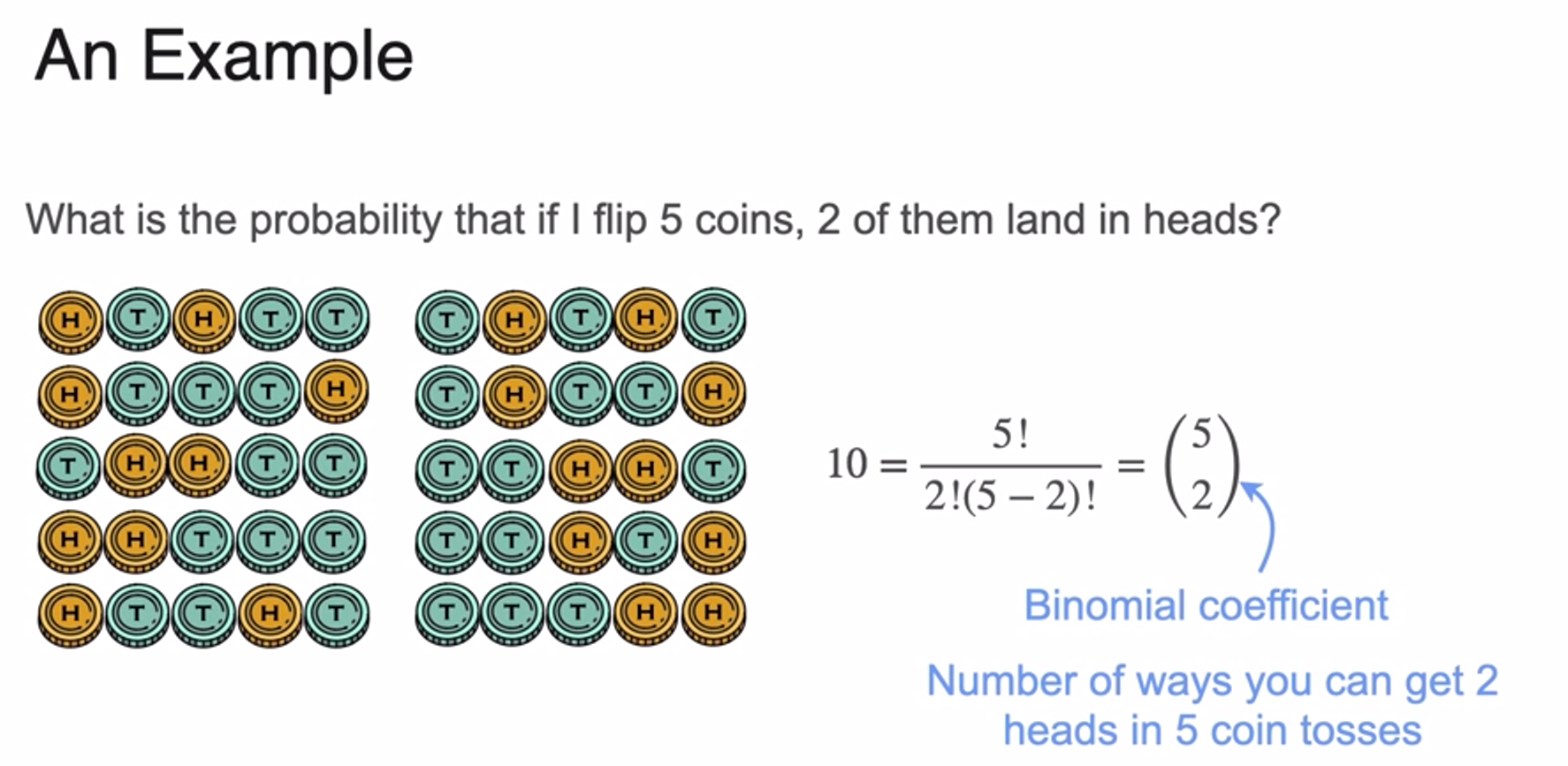
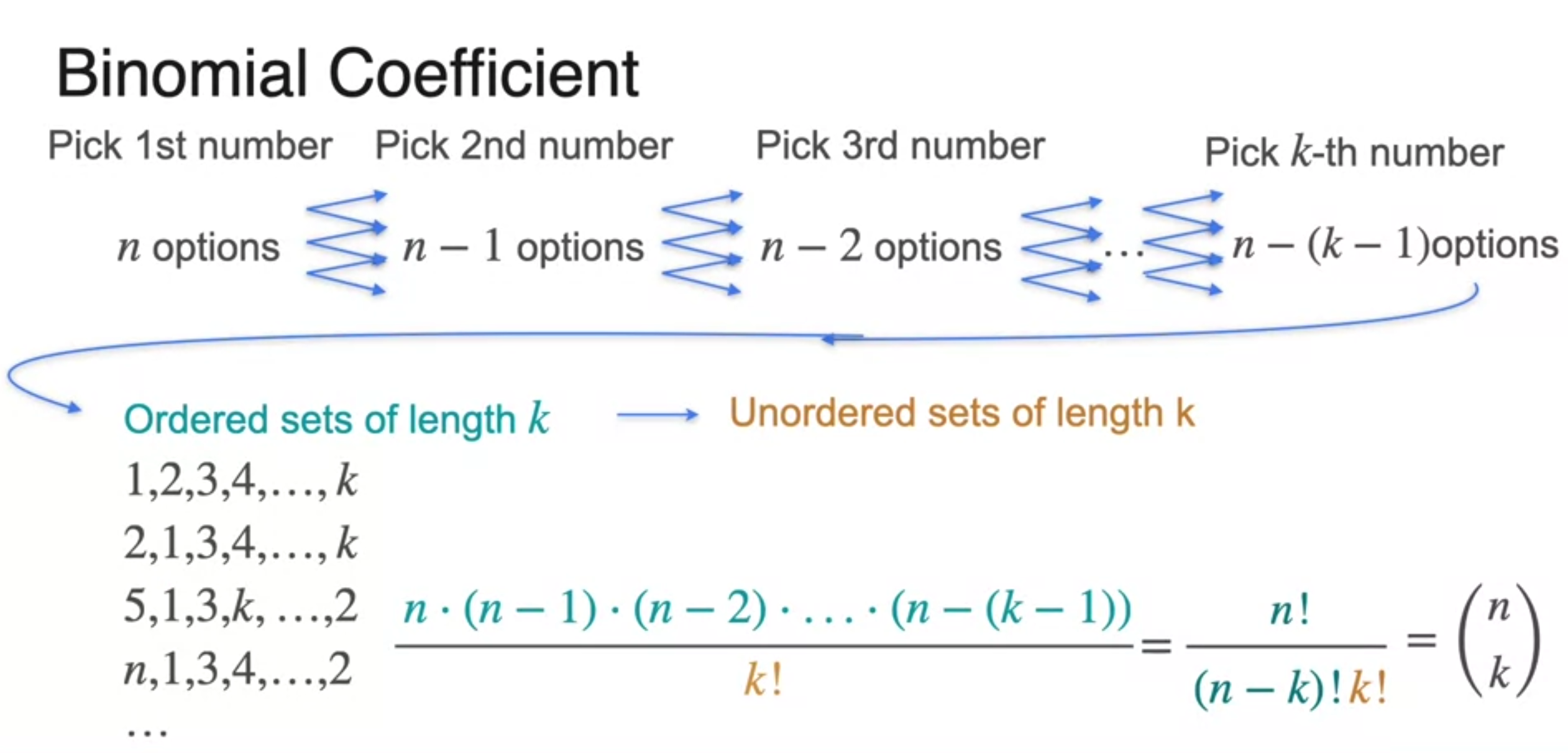
(Optional) Binomial Coefficient


Bernoulli Distribution
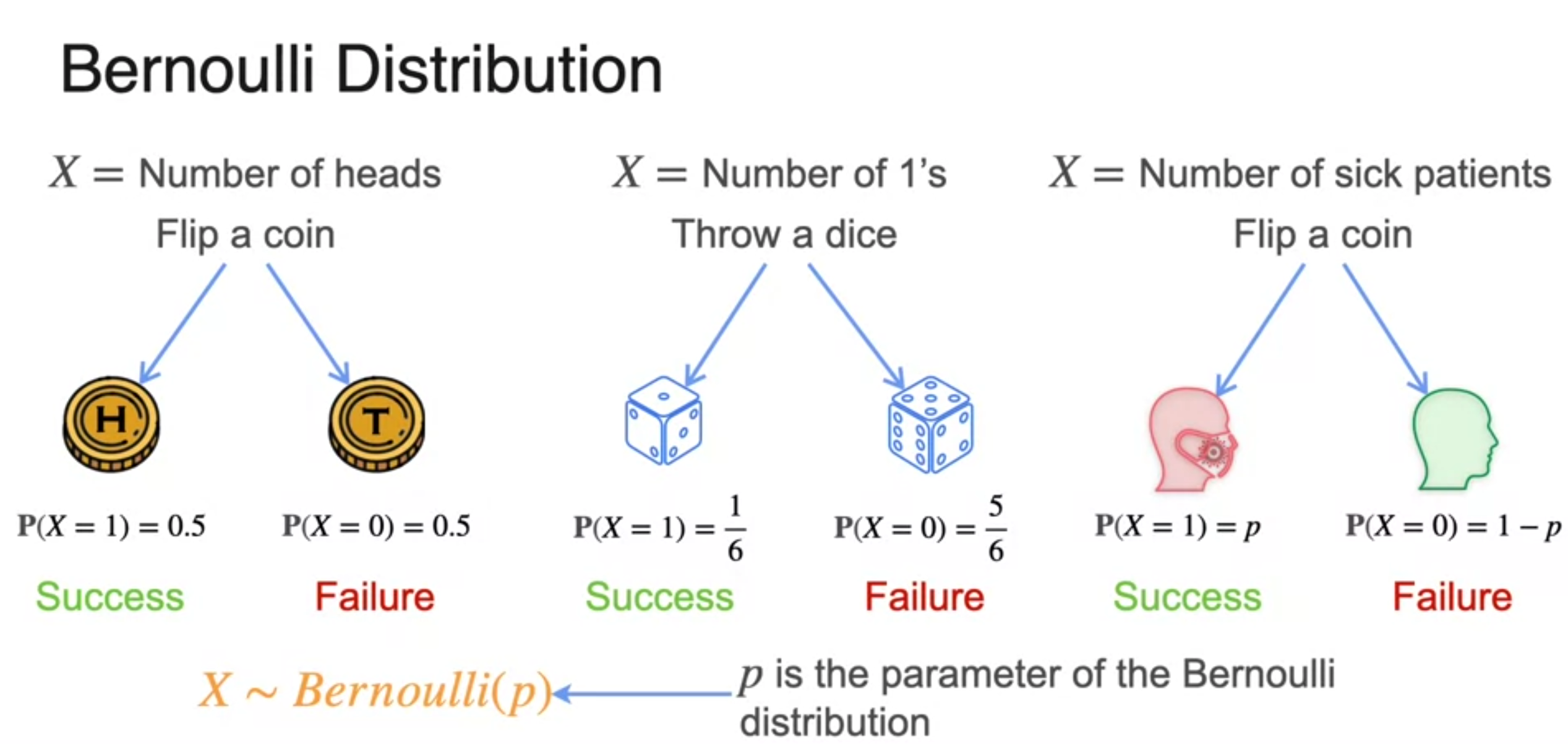
- 베르누이 분포는 한개의 파라미터만을 갖는다. 그것은 성공 확률인 p.
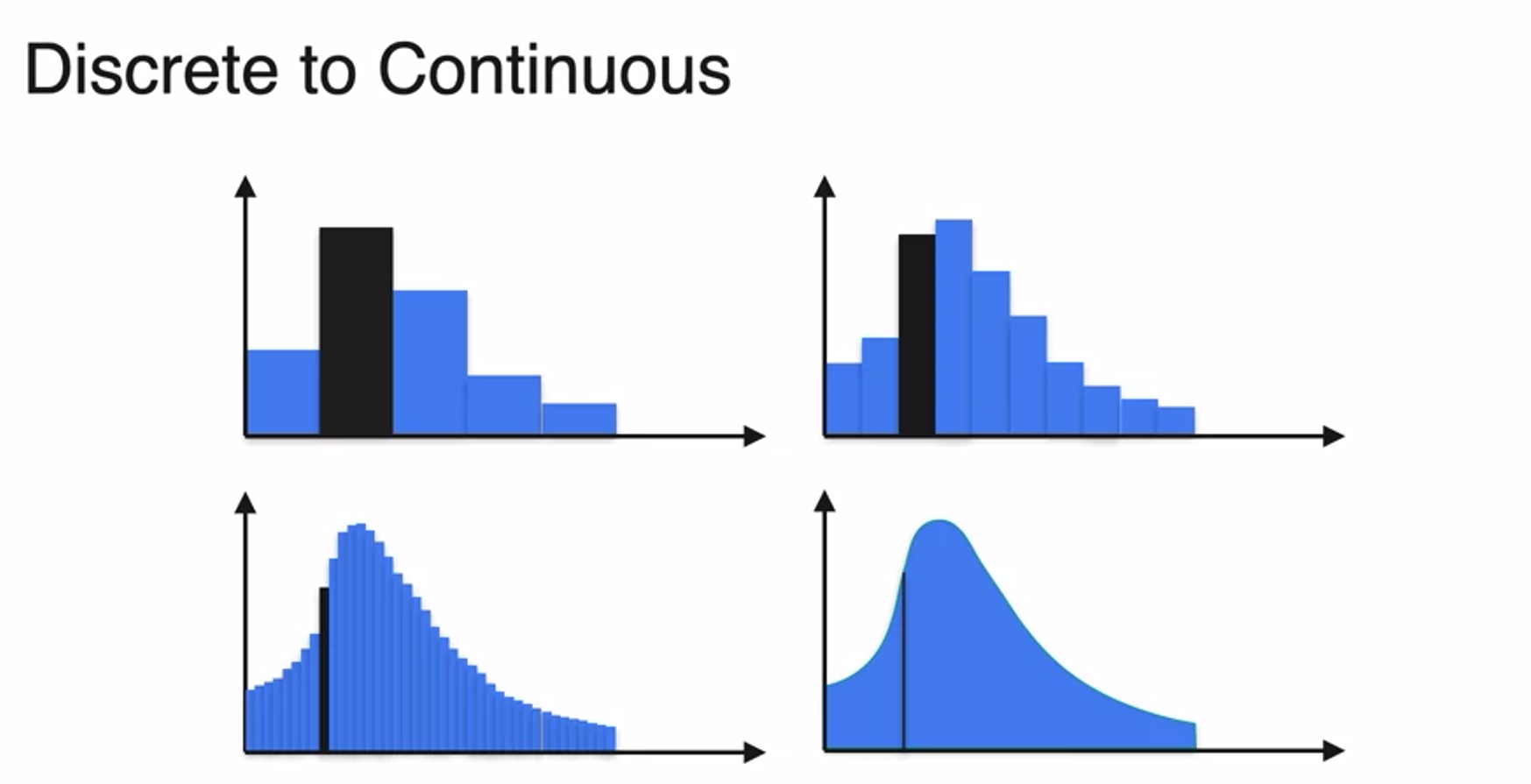
Probability Distributions (Continuous)
- we did discrete distribution 이산분포
- 불연속적인, 유한하고 셀 수 있는 확률분포
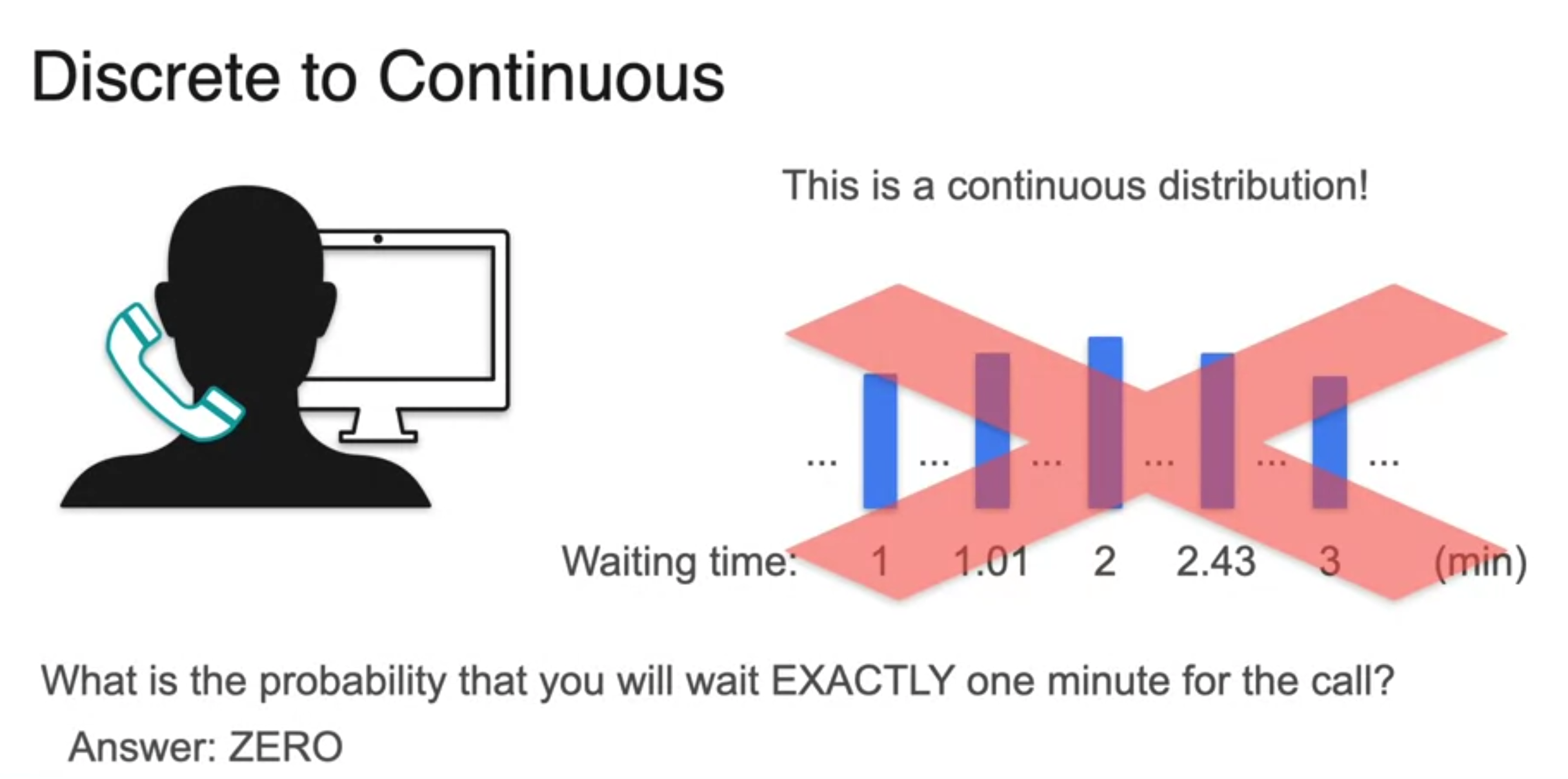
- near zero
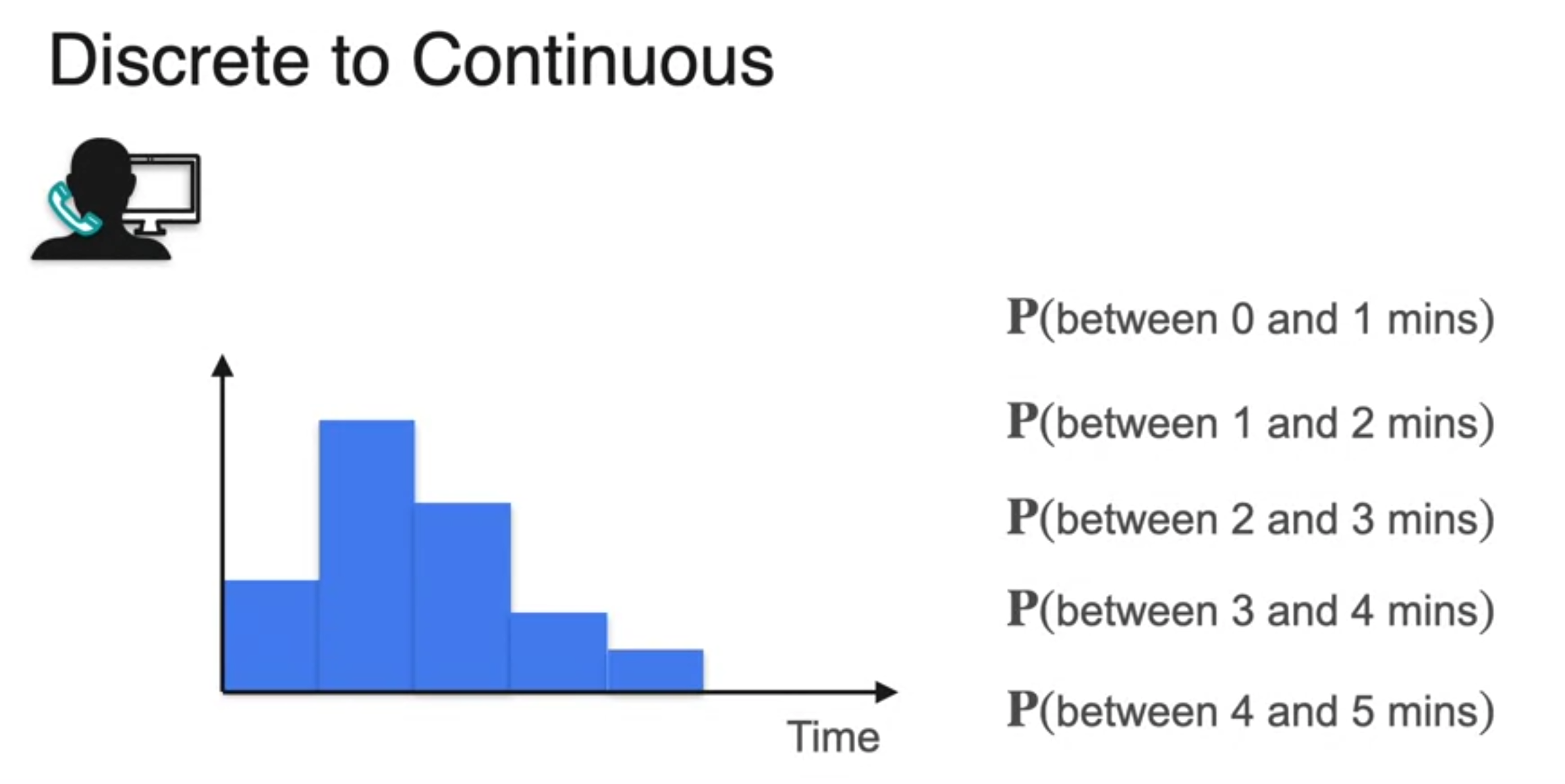
- 더 정밀하게! little more granular
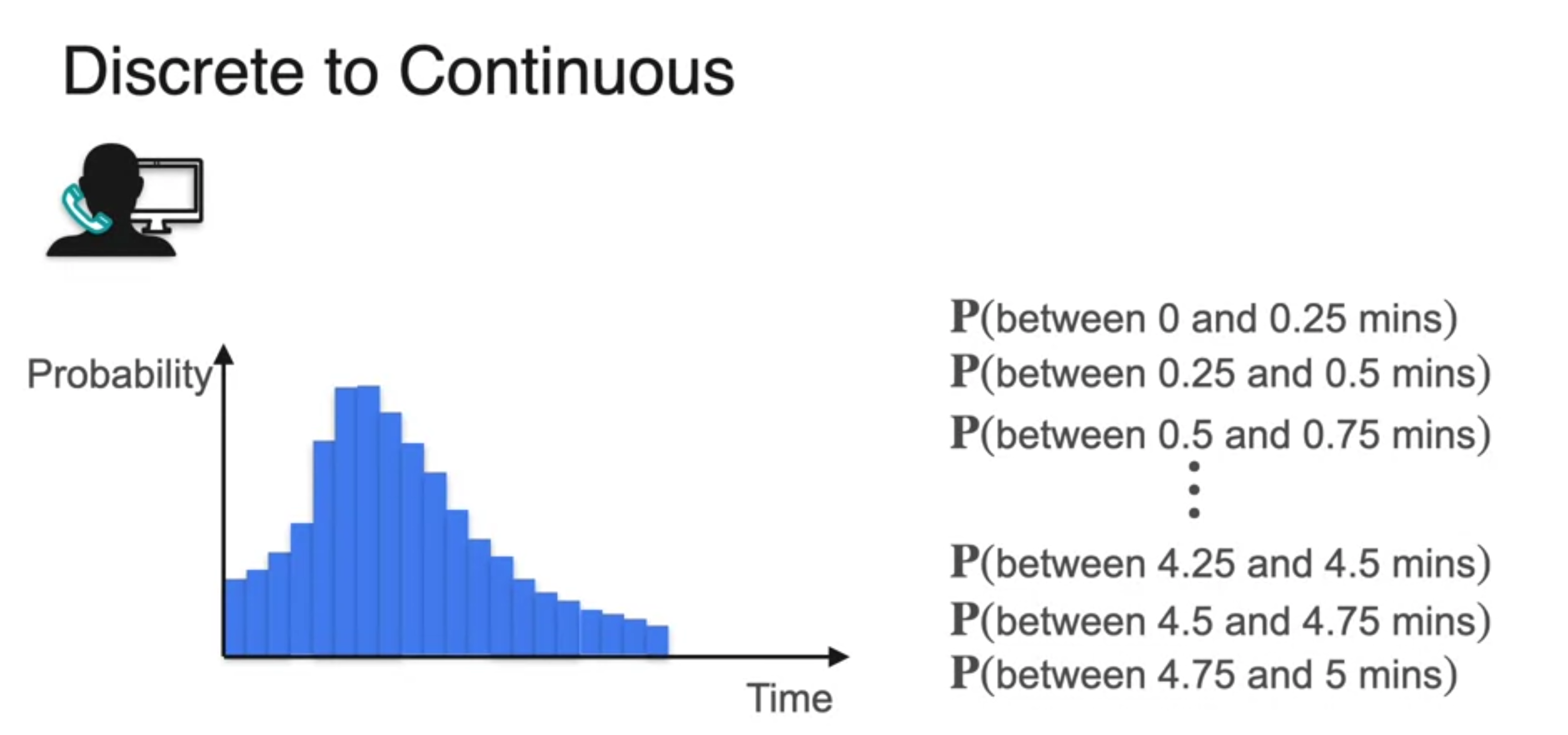
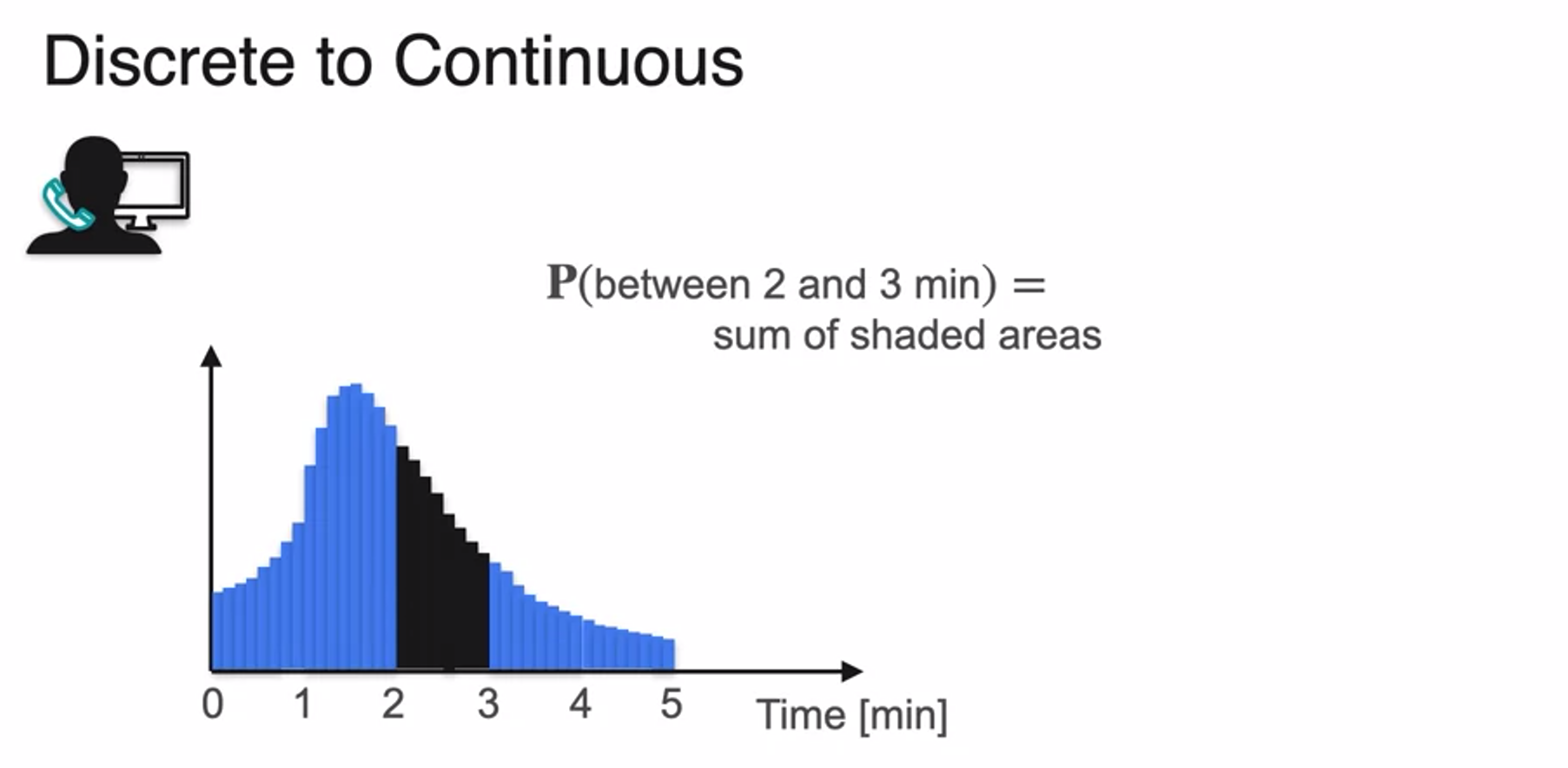
- 연속 확률 분포 continuous probability distribution
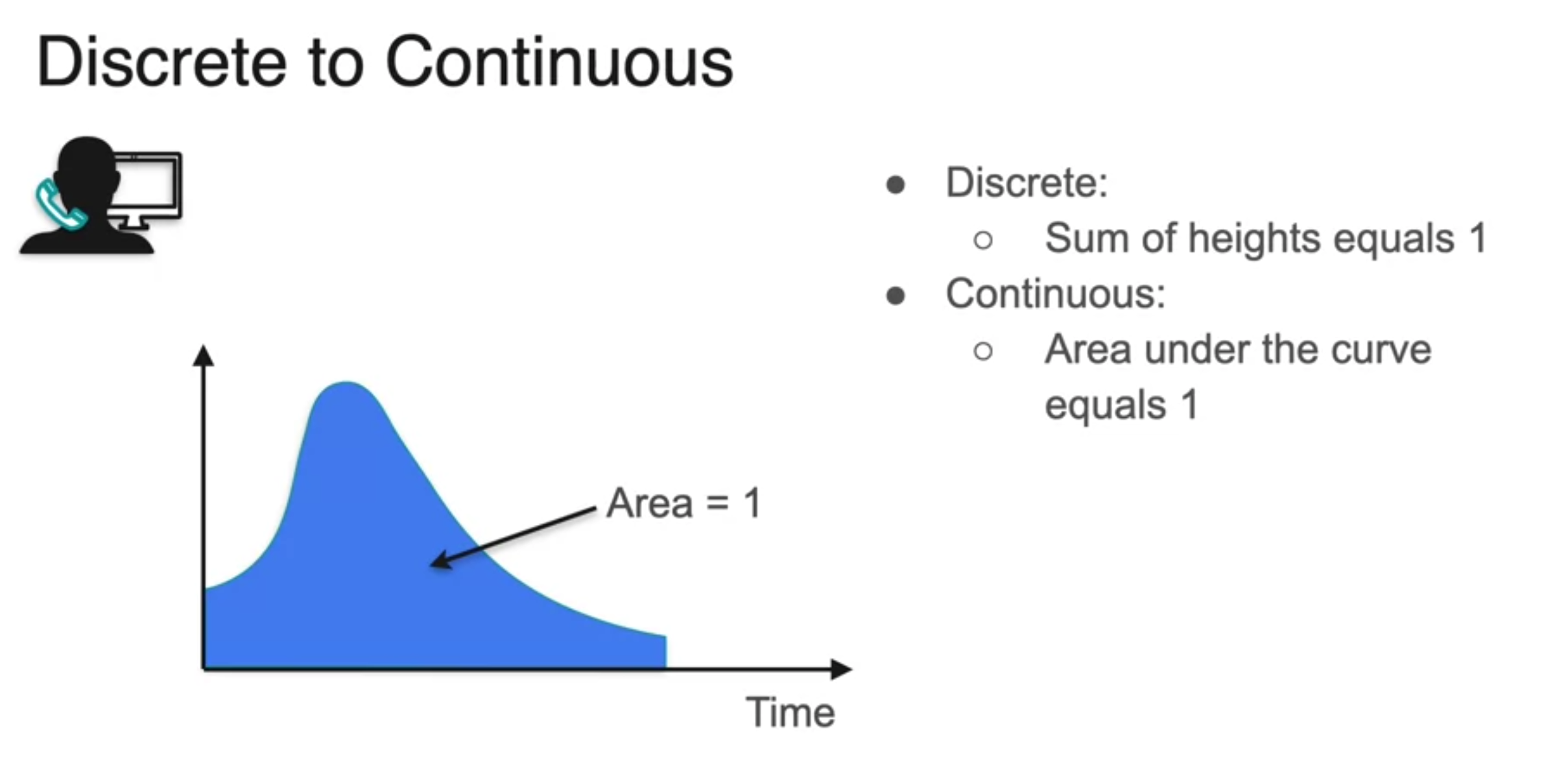
- infinite로 쪼개면 면적이 1이 되는 연속 확률 분포 형태가 됨
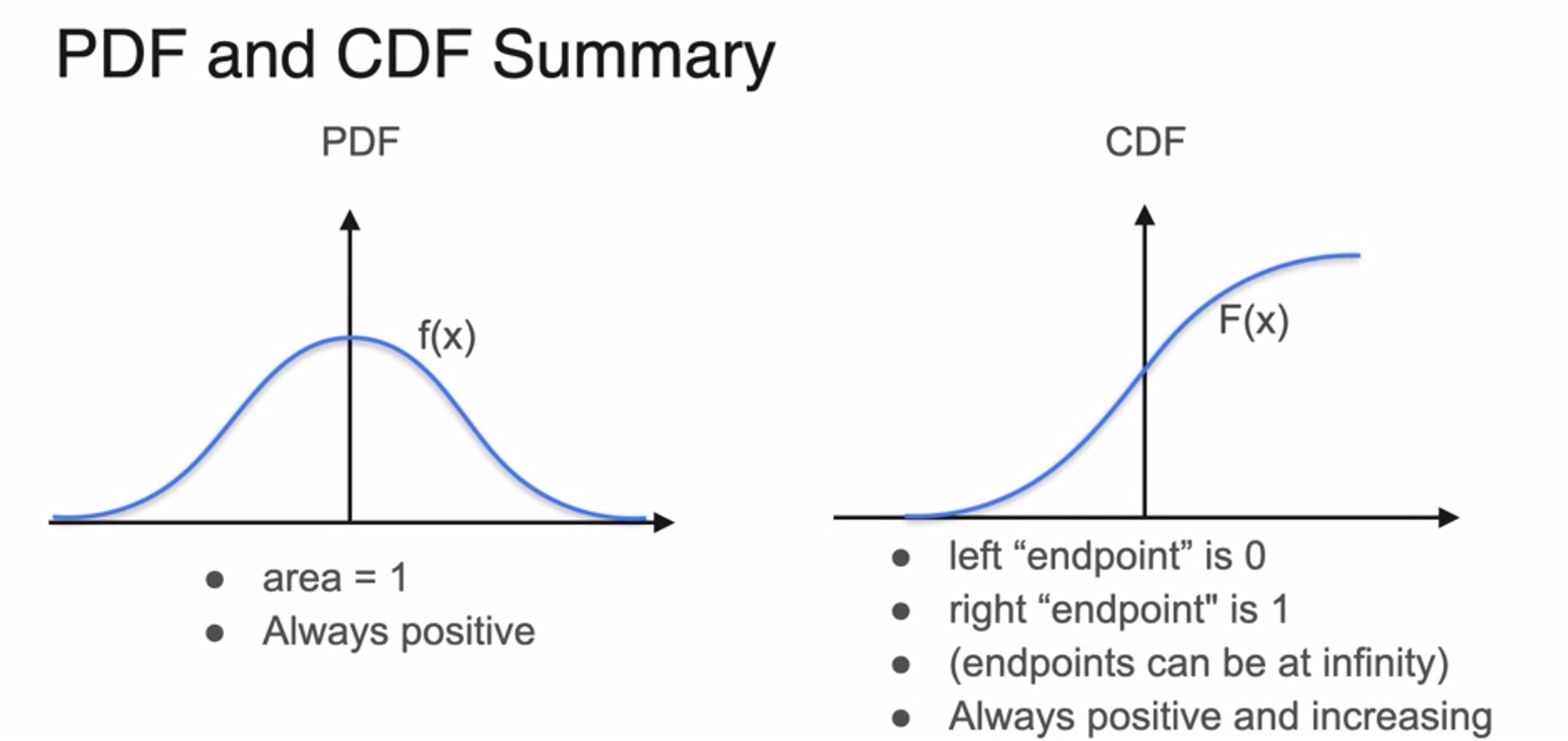
Probability Density Function
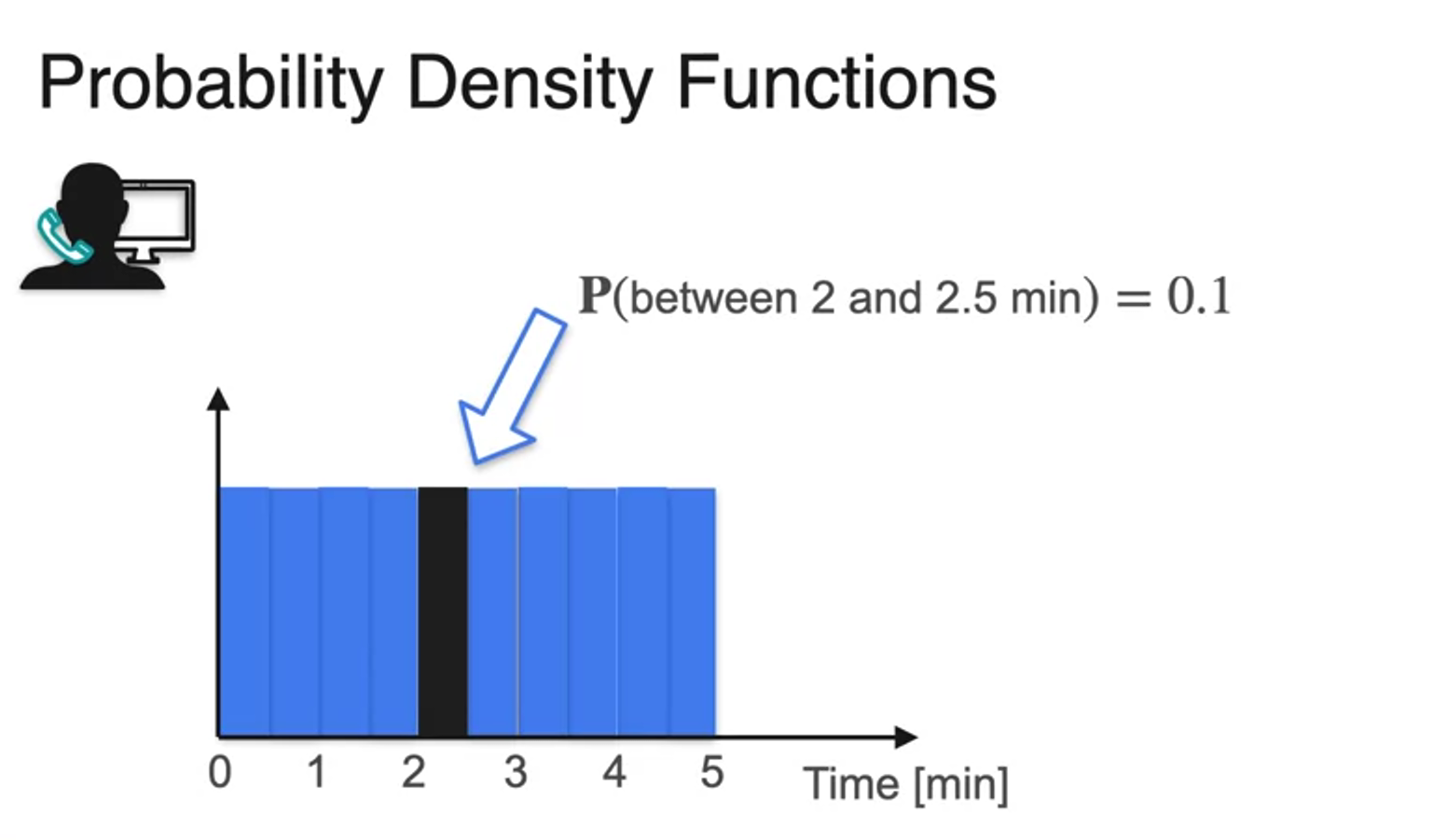
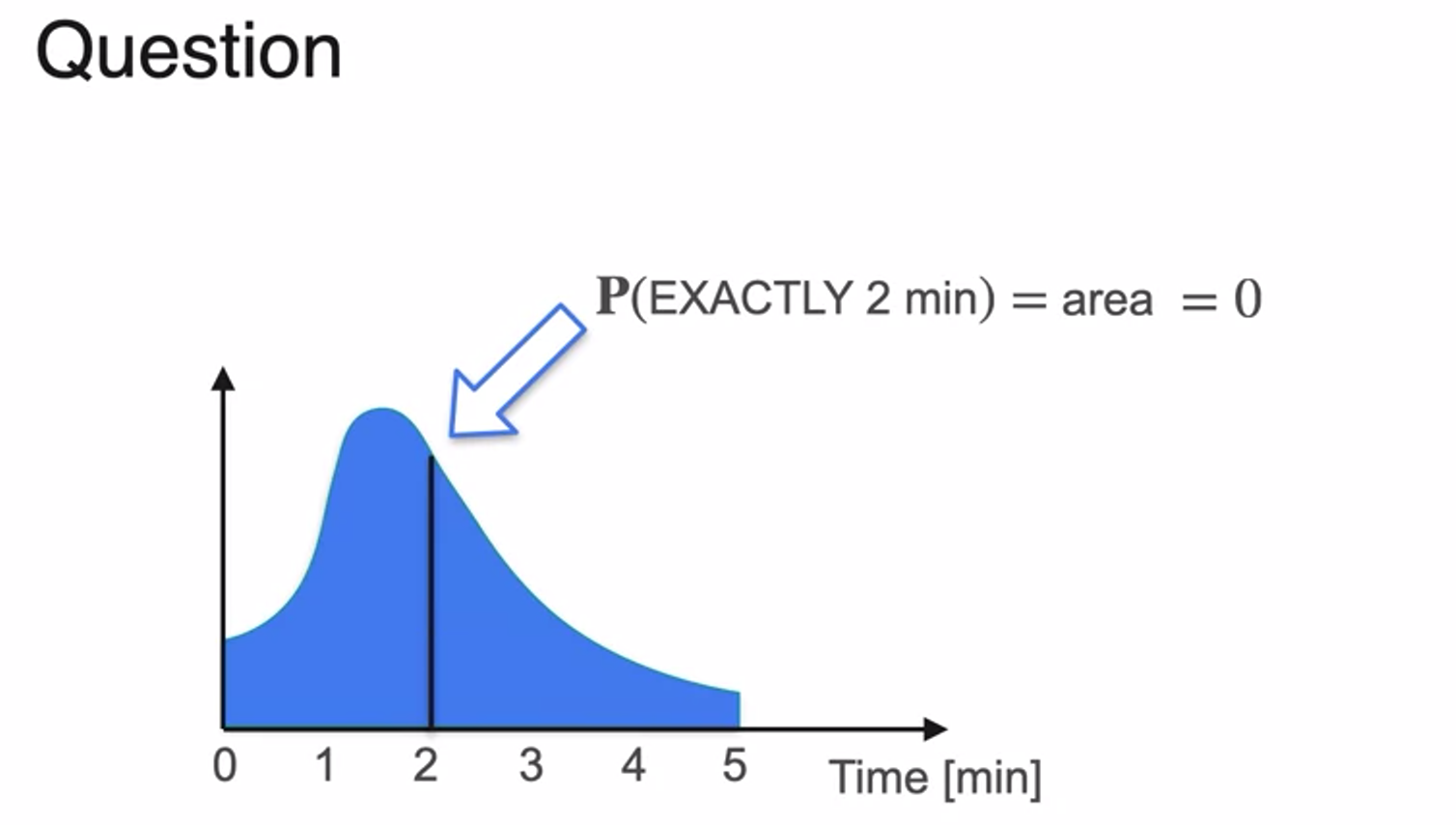


- PDF : When takes particular value, probability always 0
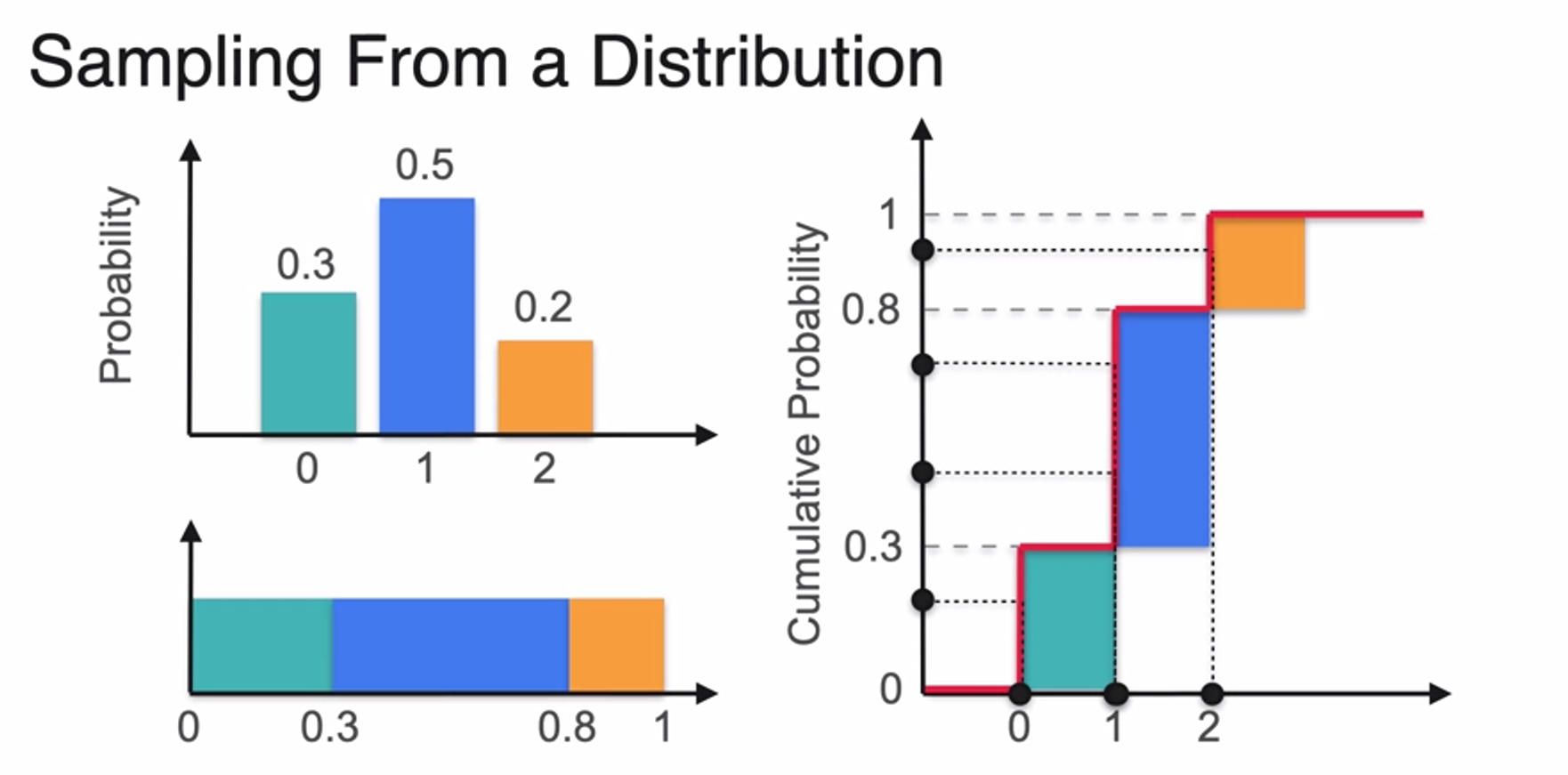
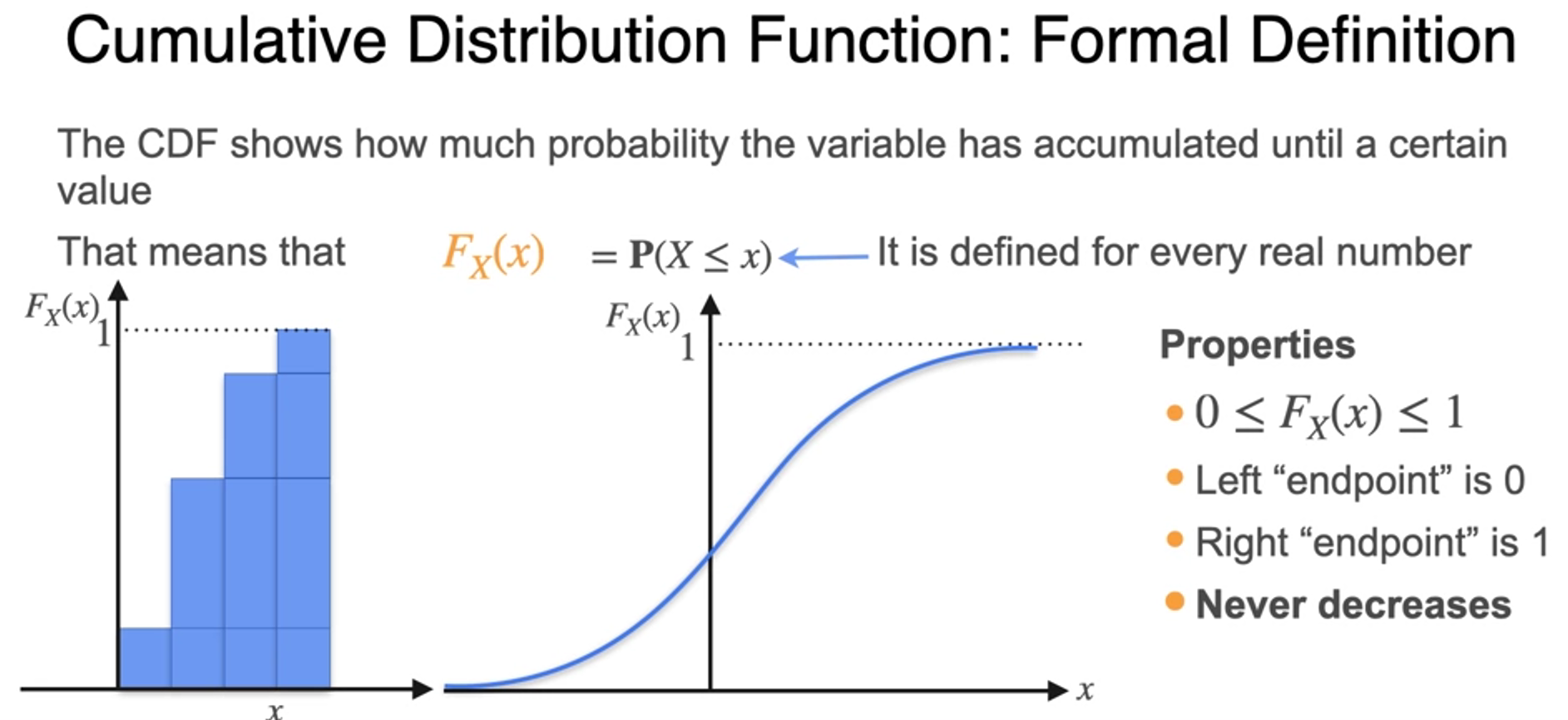
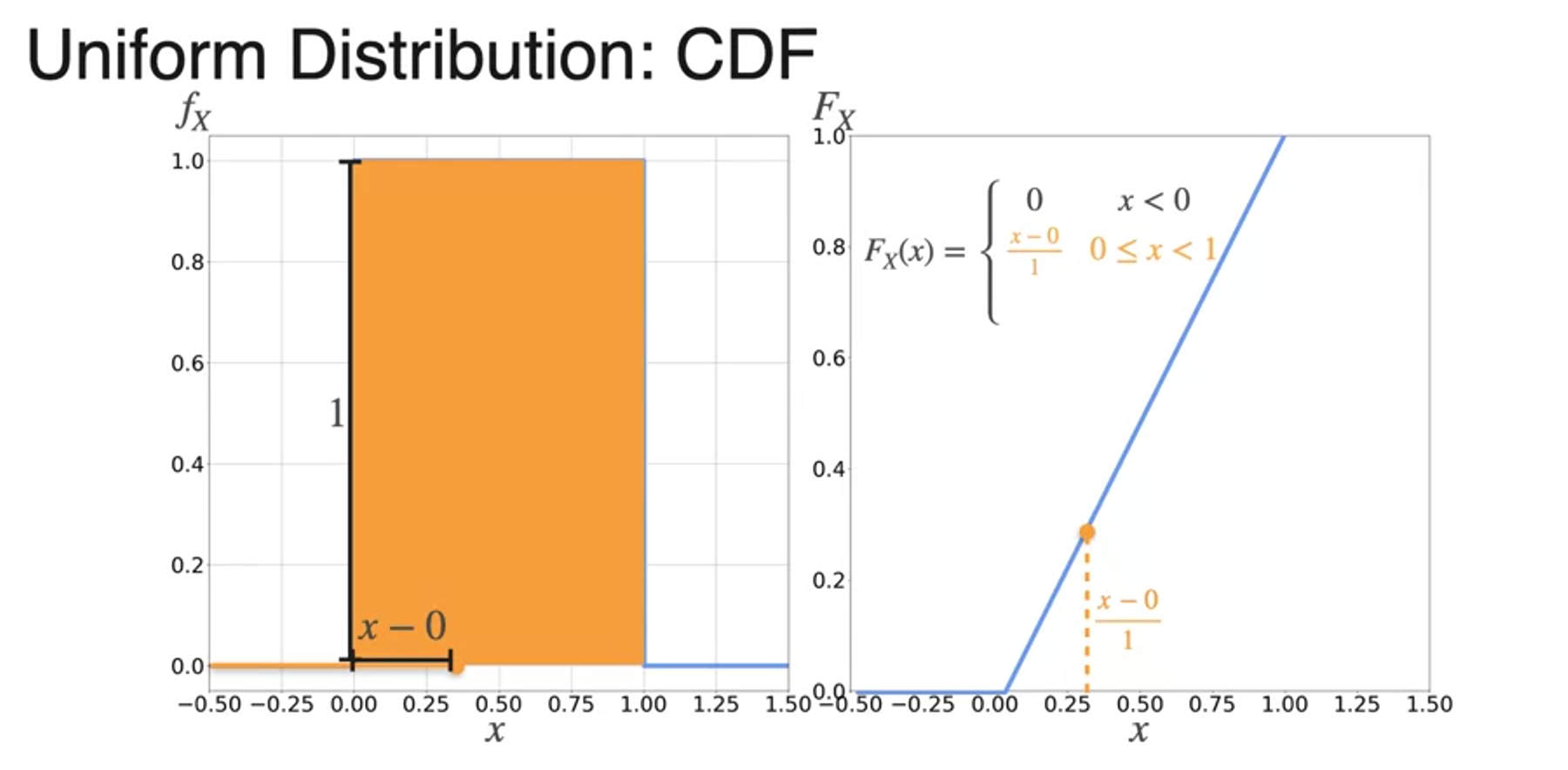
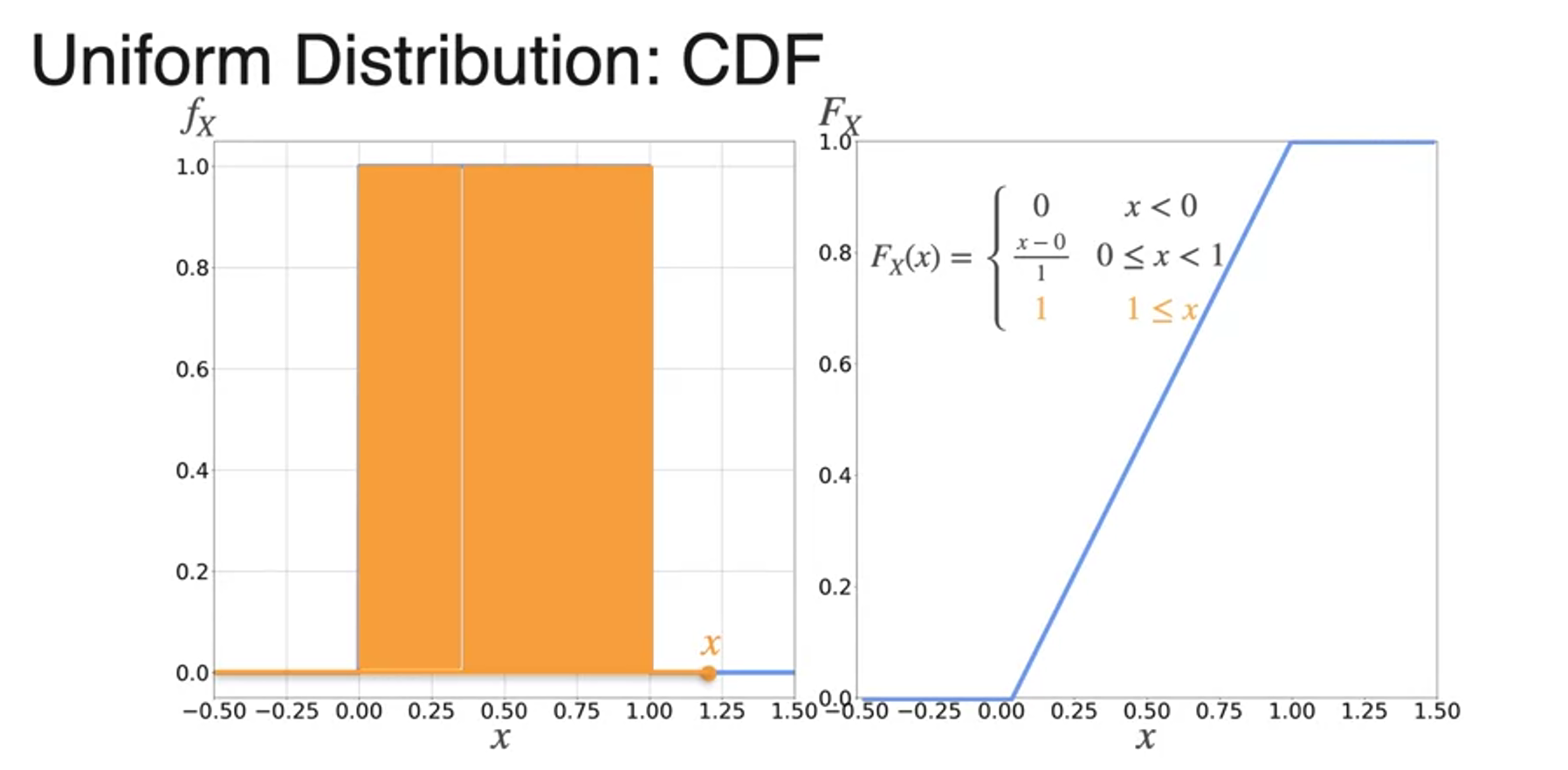
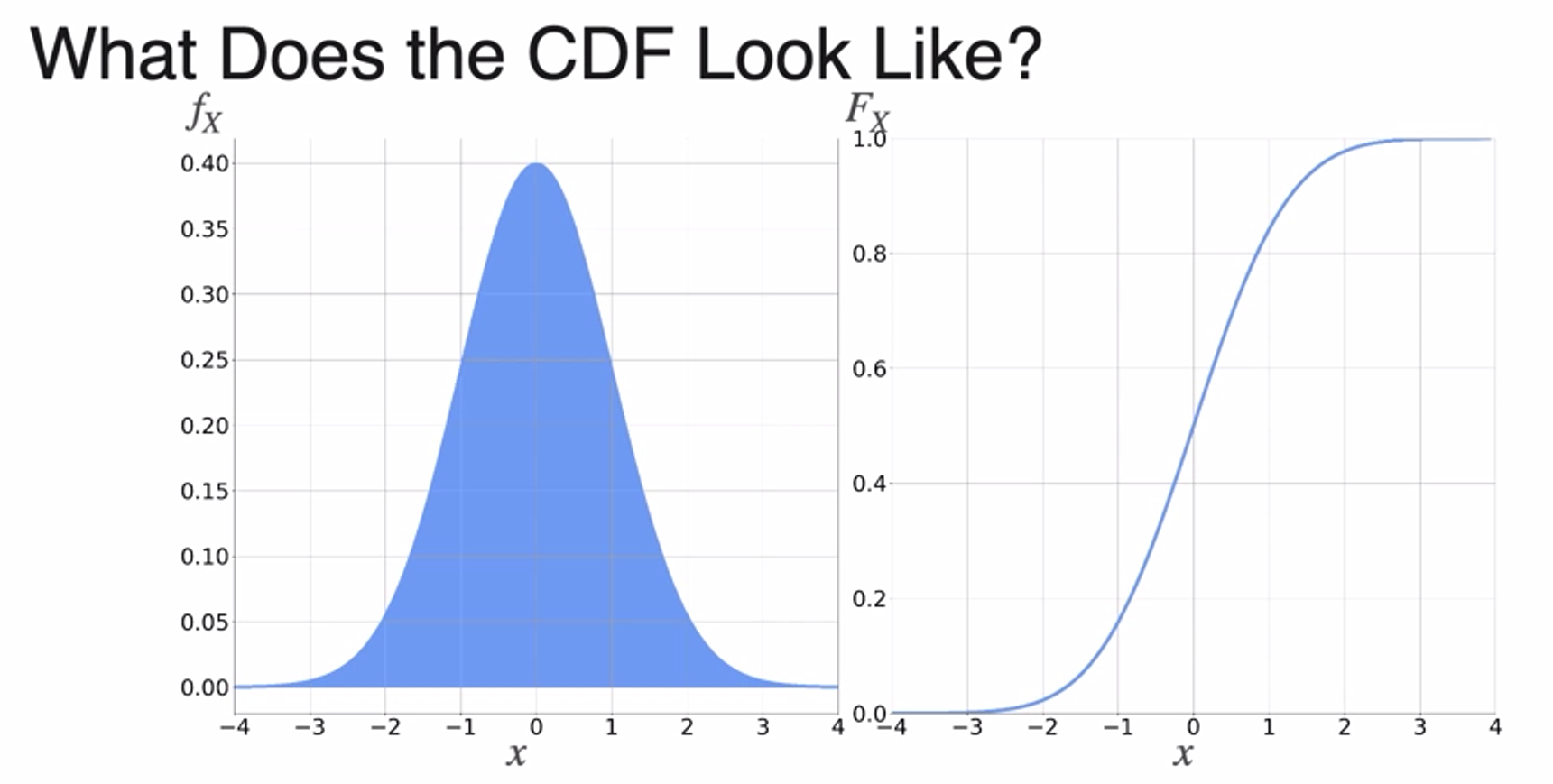
Cumulative Distribution Function
- 누적 분포 함수
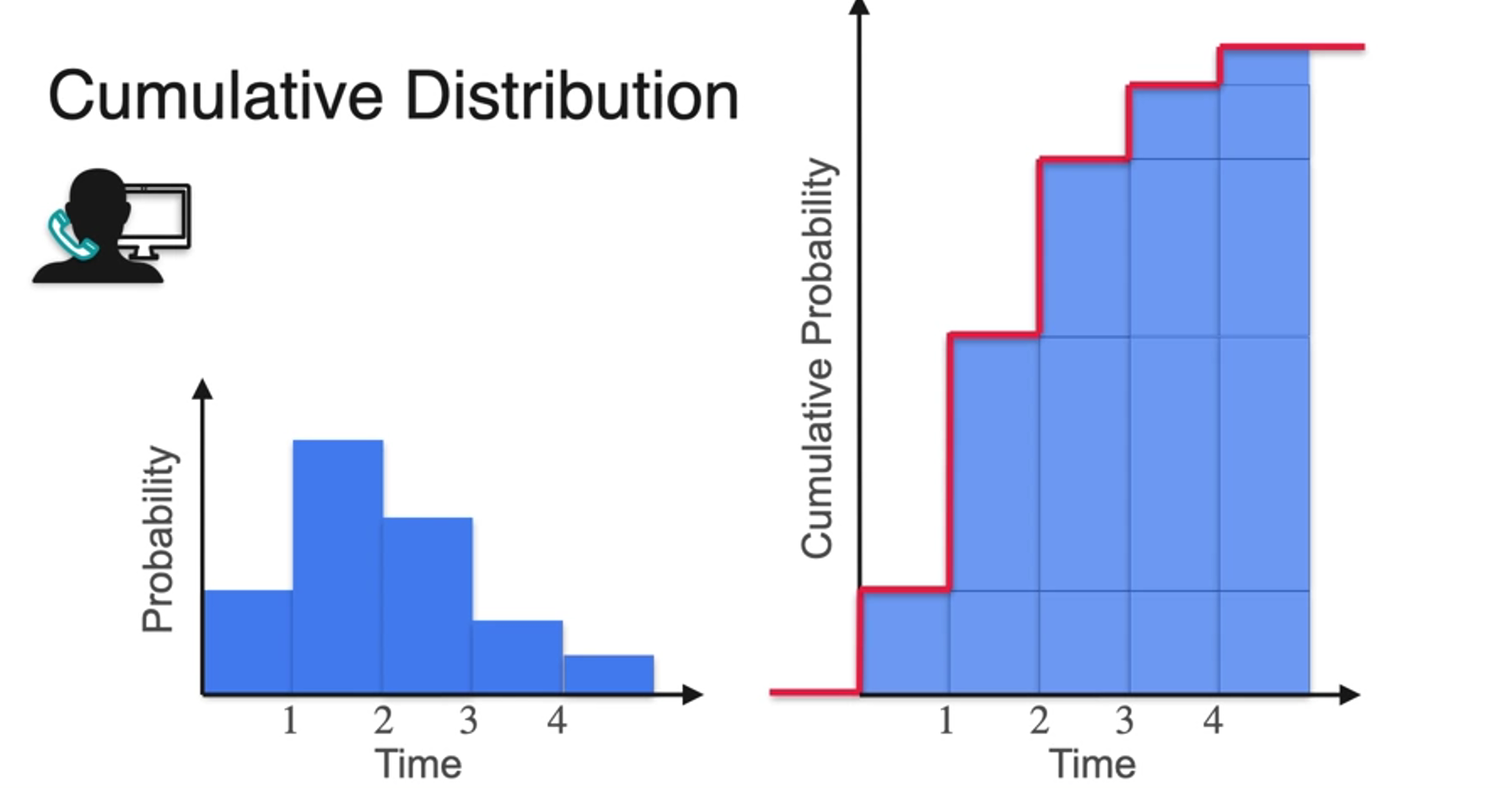
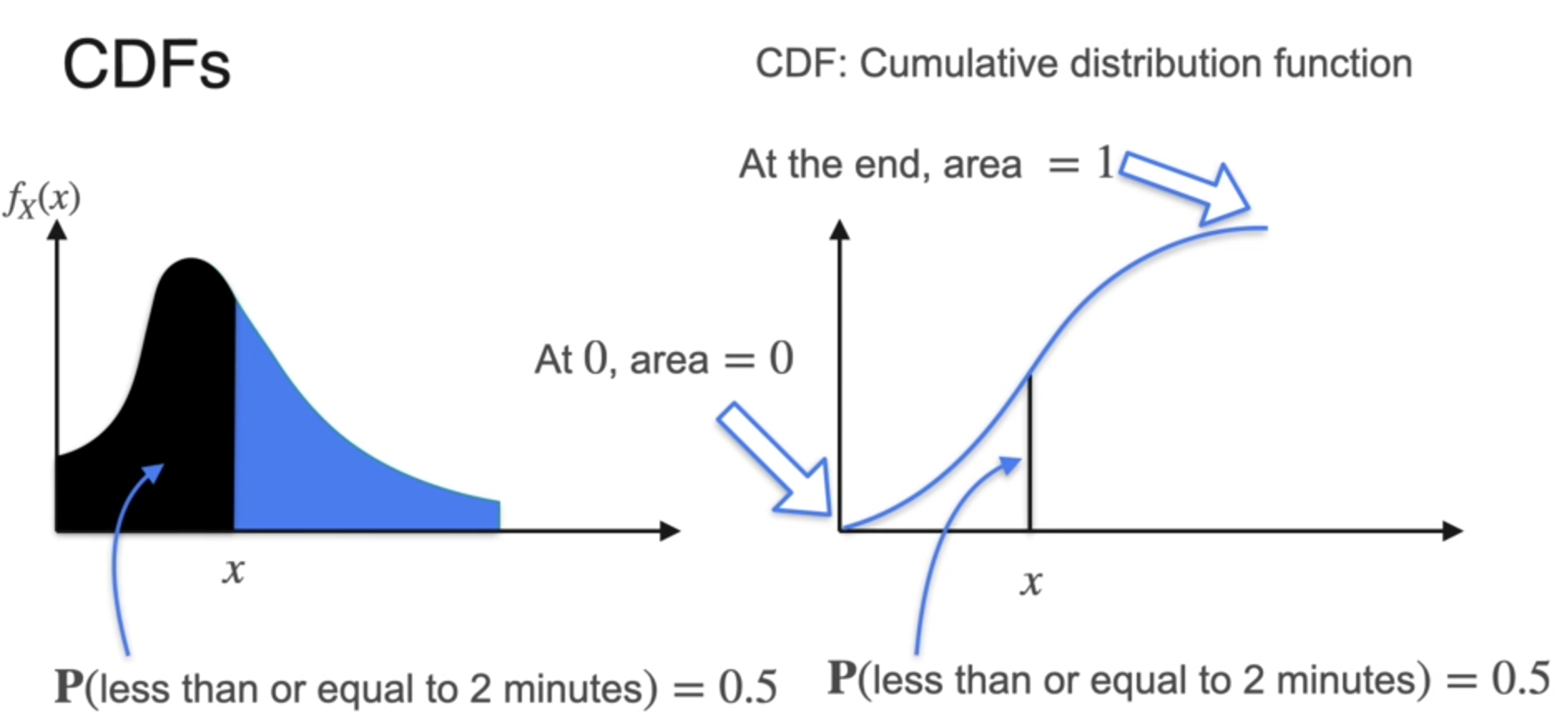
- CDF from PDF
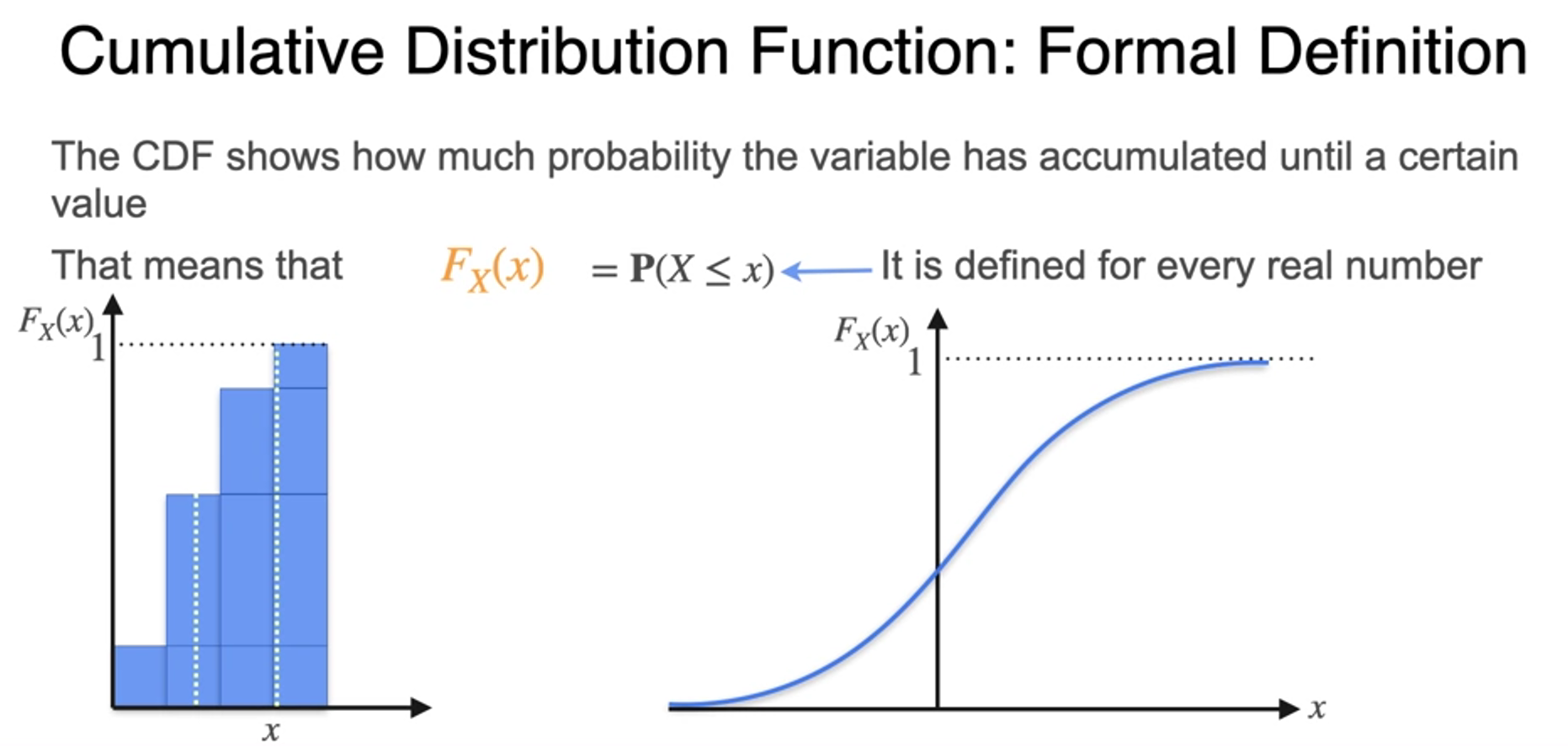
- uses capital F as formula
- for continuous variables, because there is no point of mass, you get continuous function
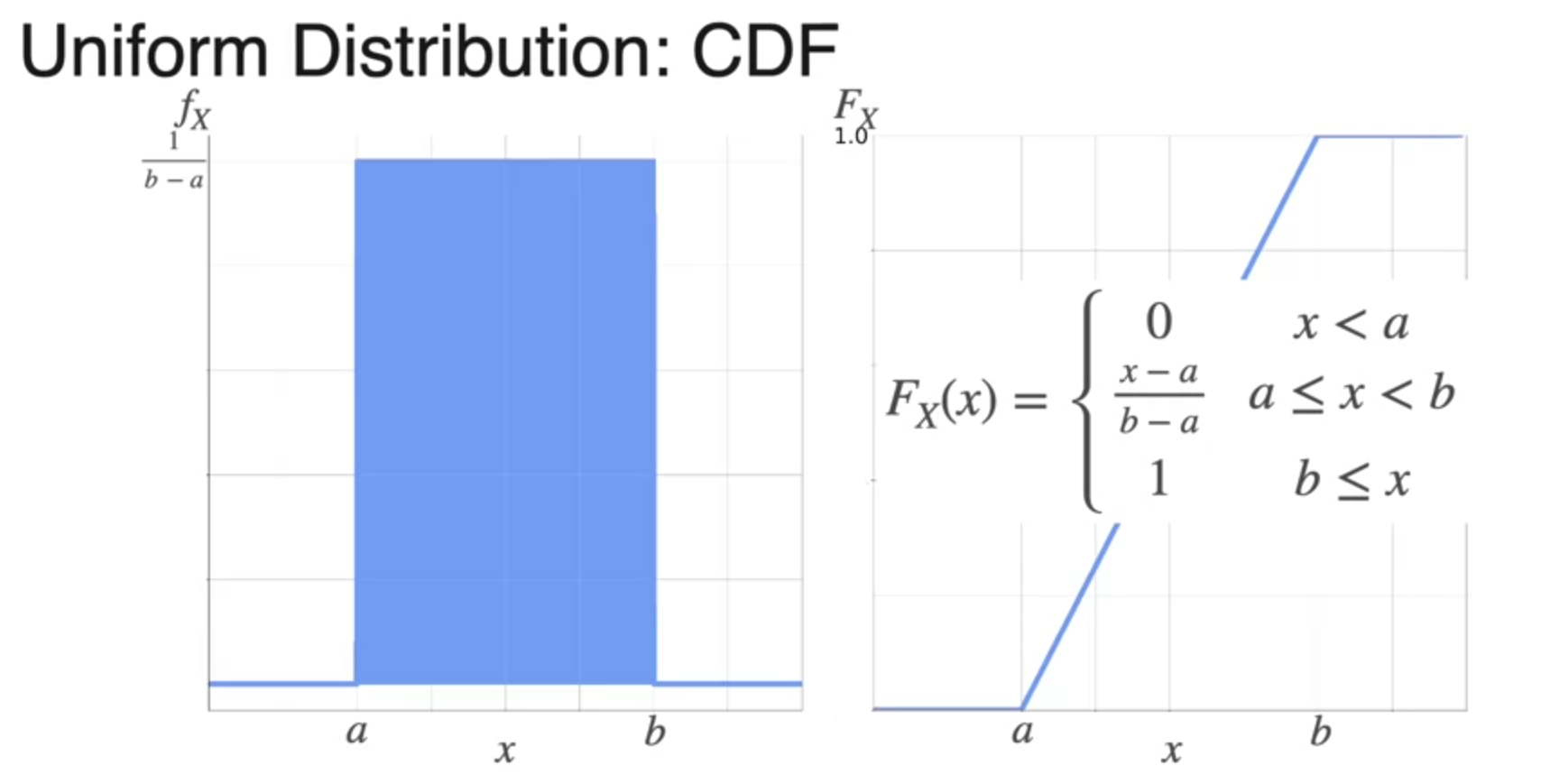
Uniform Distribution
- 균등 분포
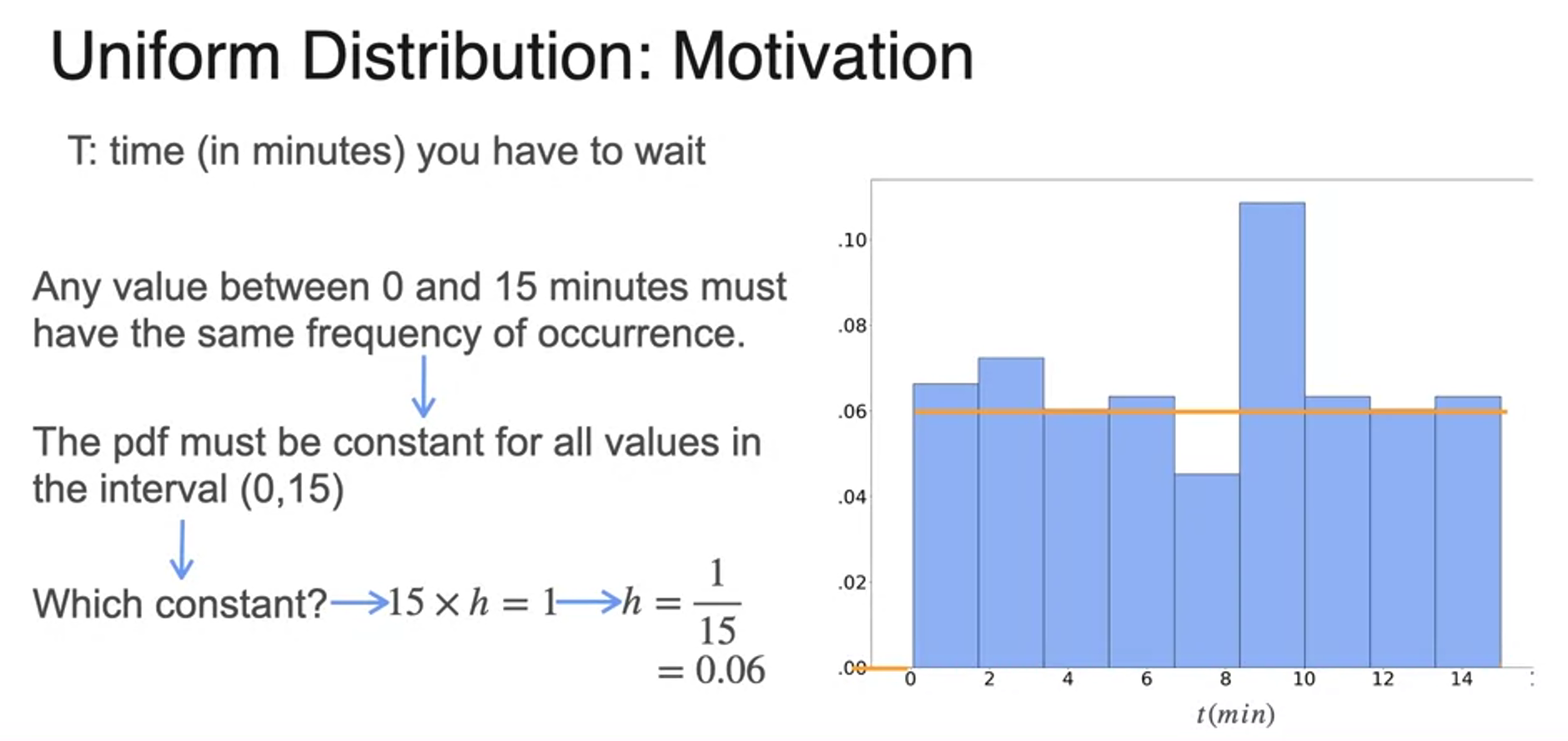
- 아래 면적의 합은 1이어야 하므로

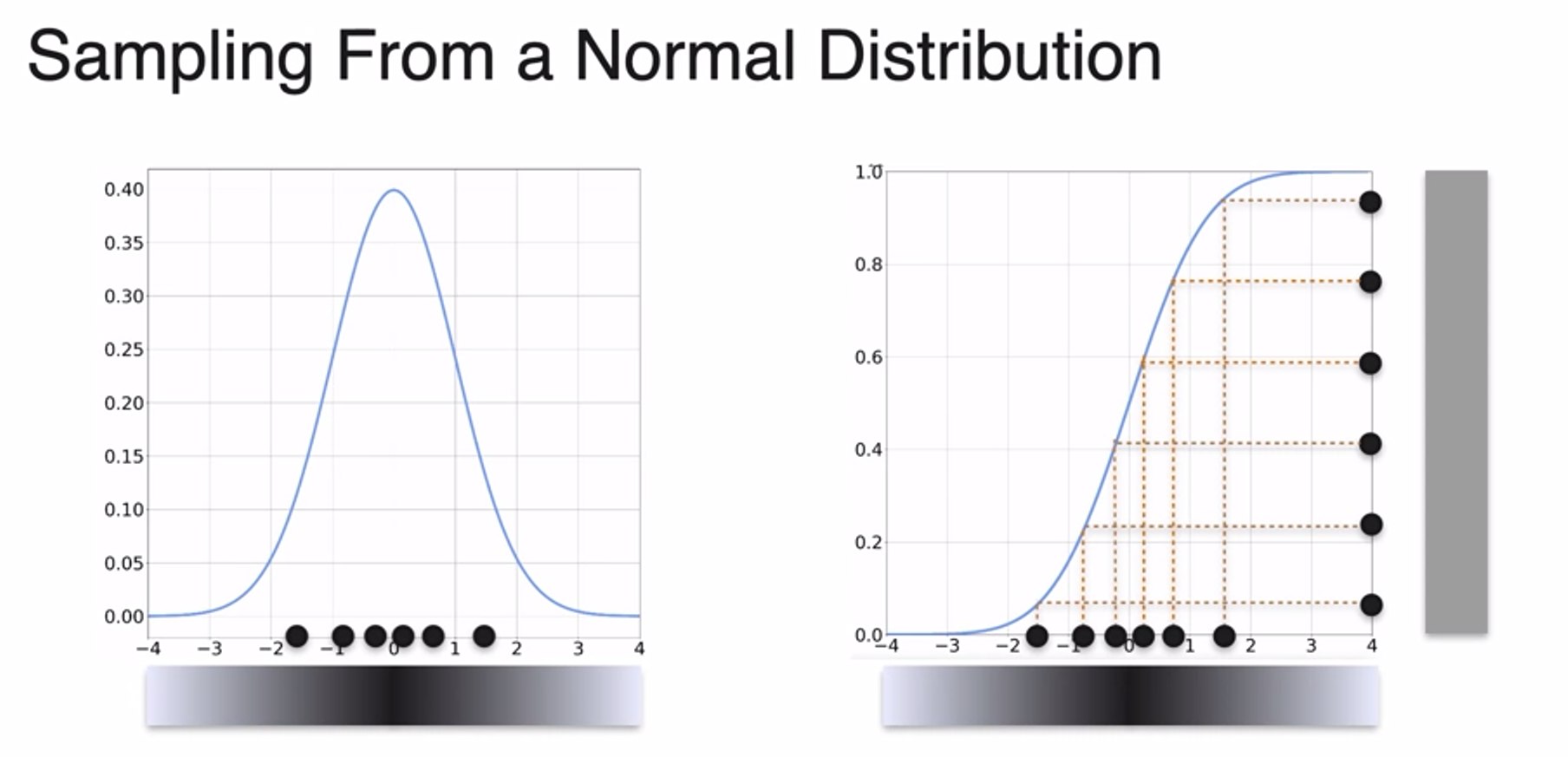
Normal Distribution
- 정규 분포;가우시안 분포
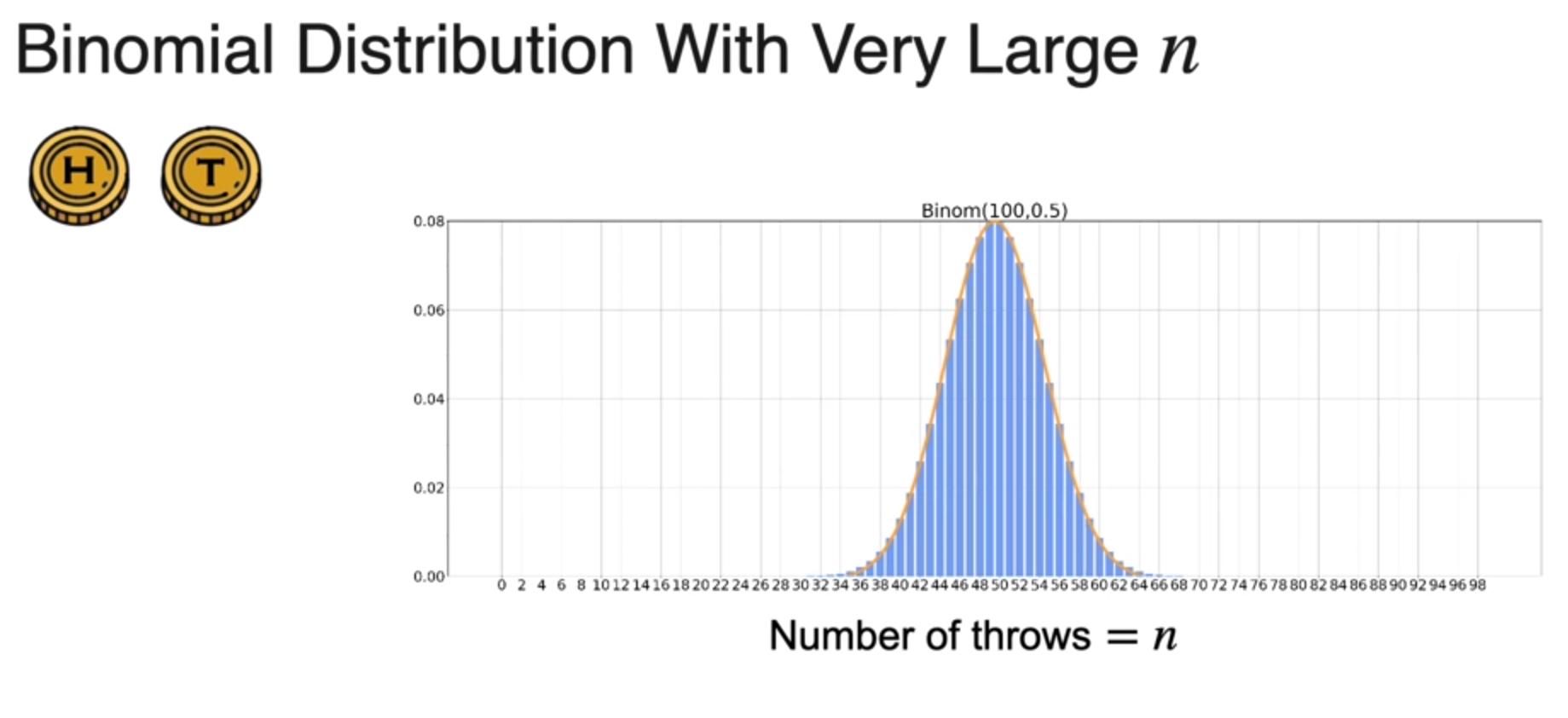
- n이 매우 클때 가우시안 분포로 이항 분포를 근사할approxmiate 수 있다.
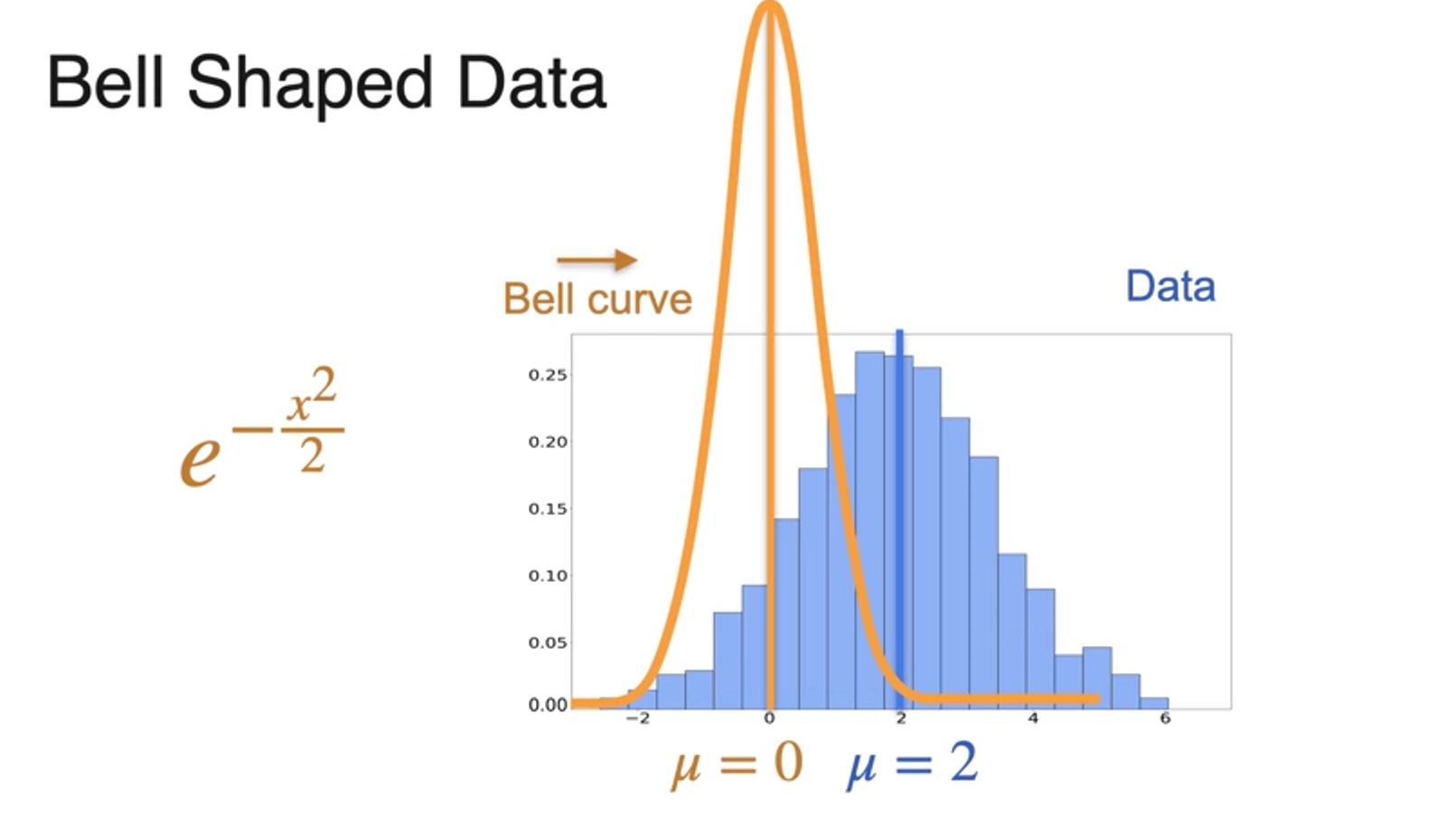
- move to right
- subtracting
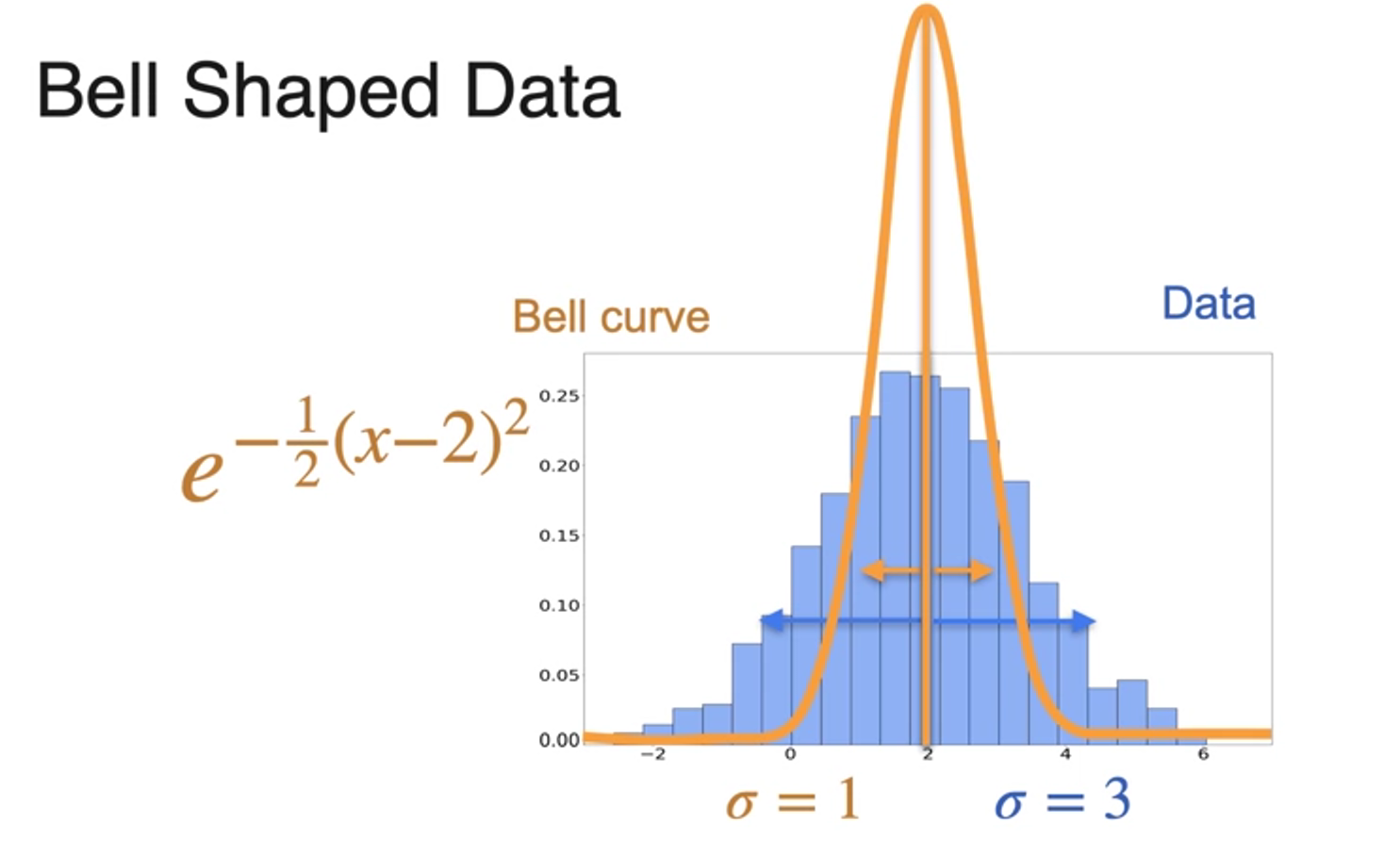
- thiken
- divide exponent
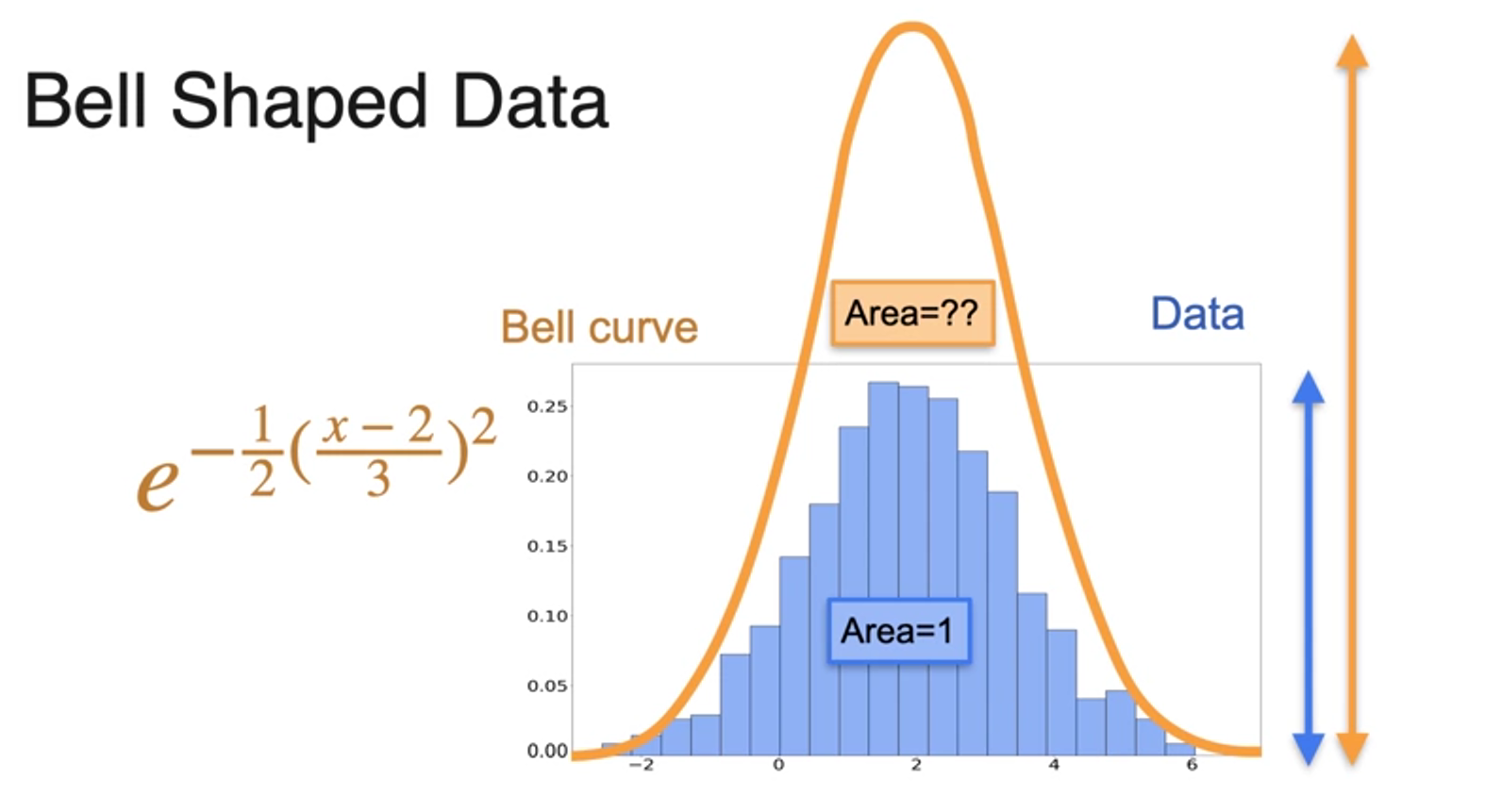
- area is not same
- divide by area
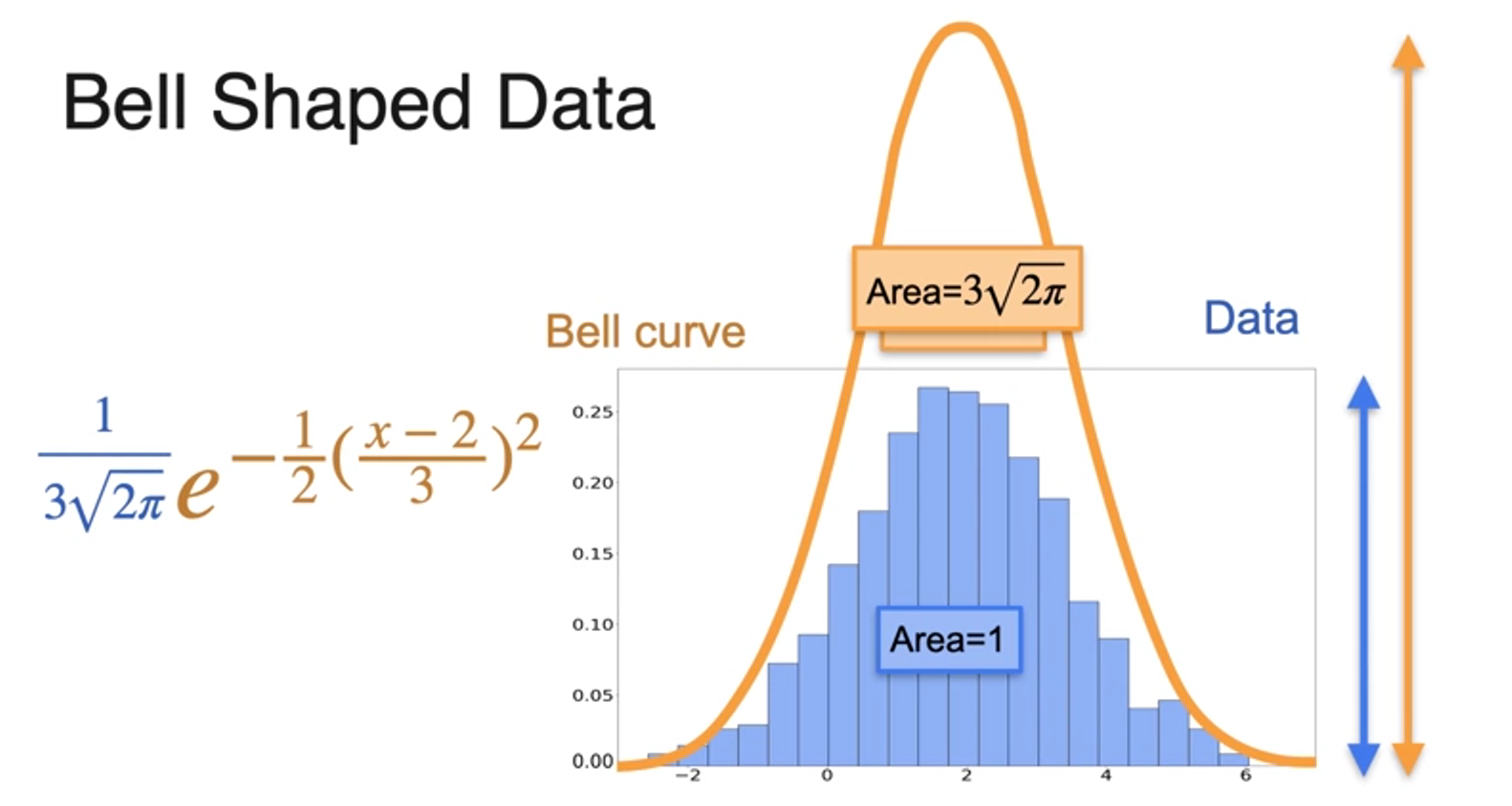
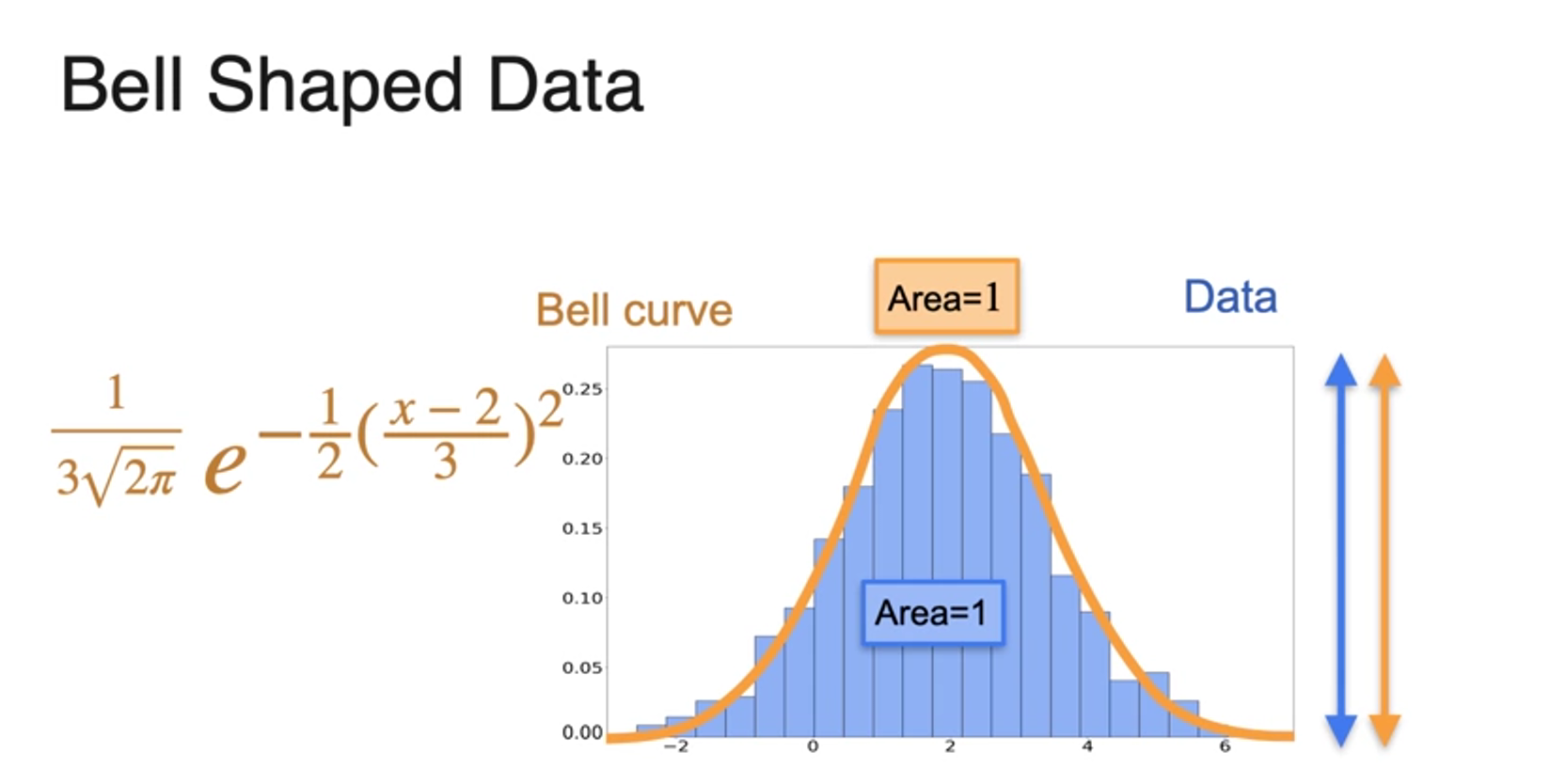
- = mean 데이터의 평균
- = standard deviation 표준편차
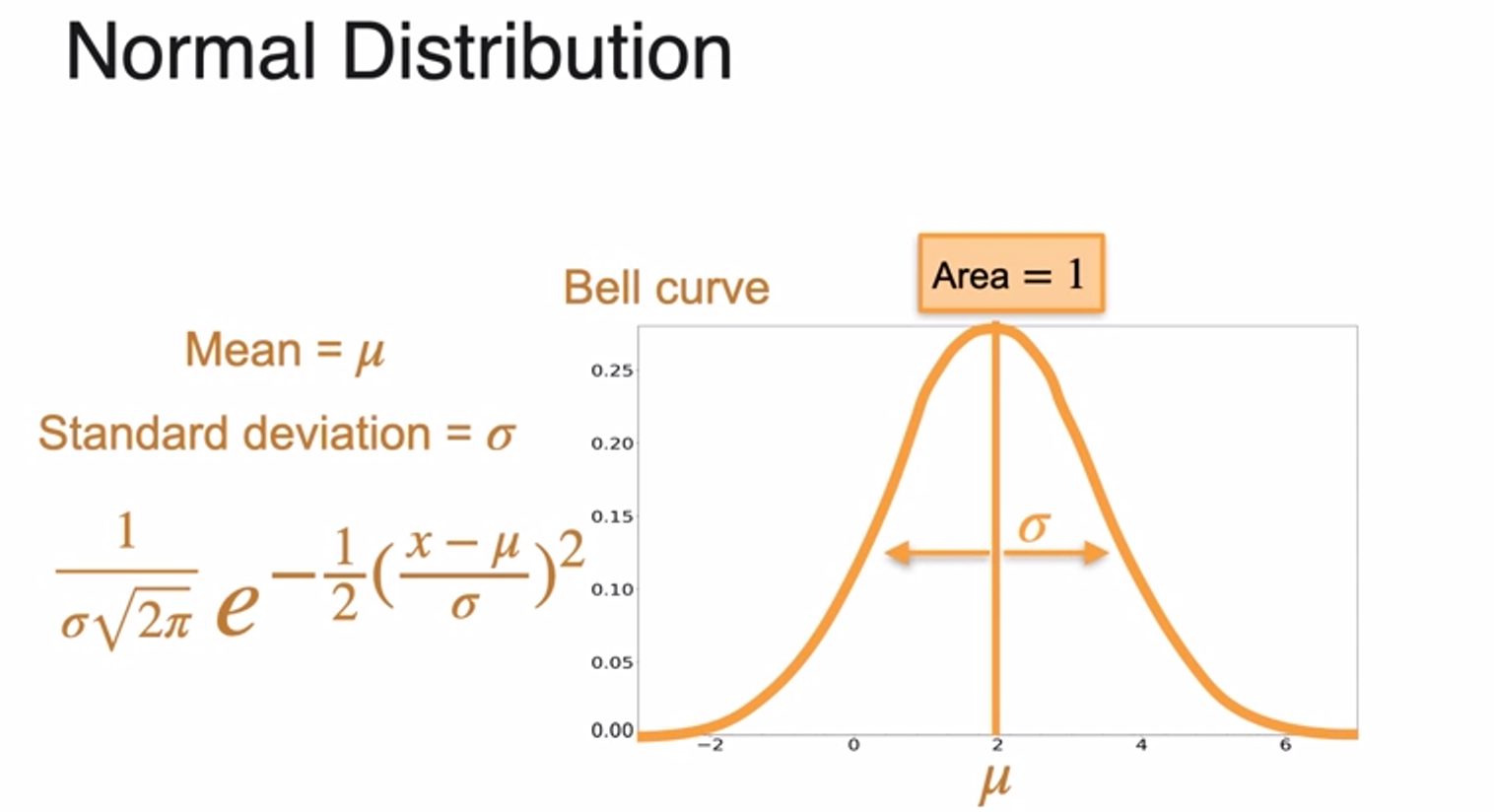
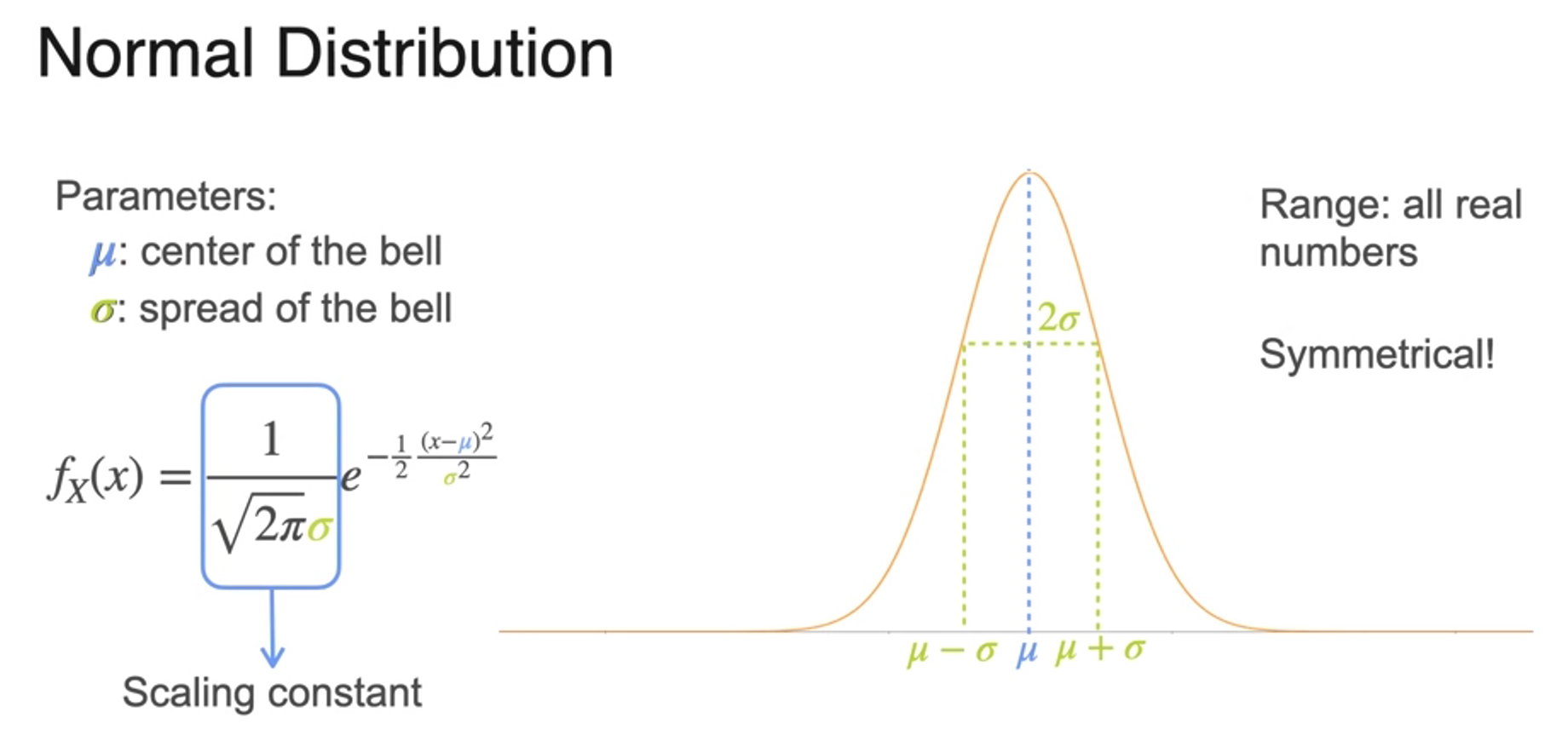
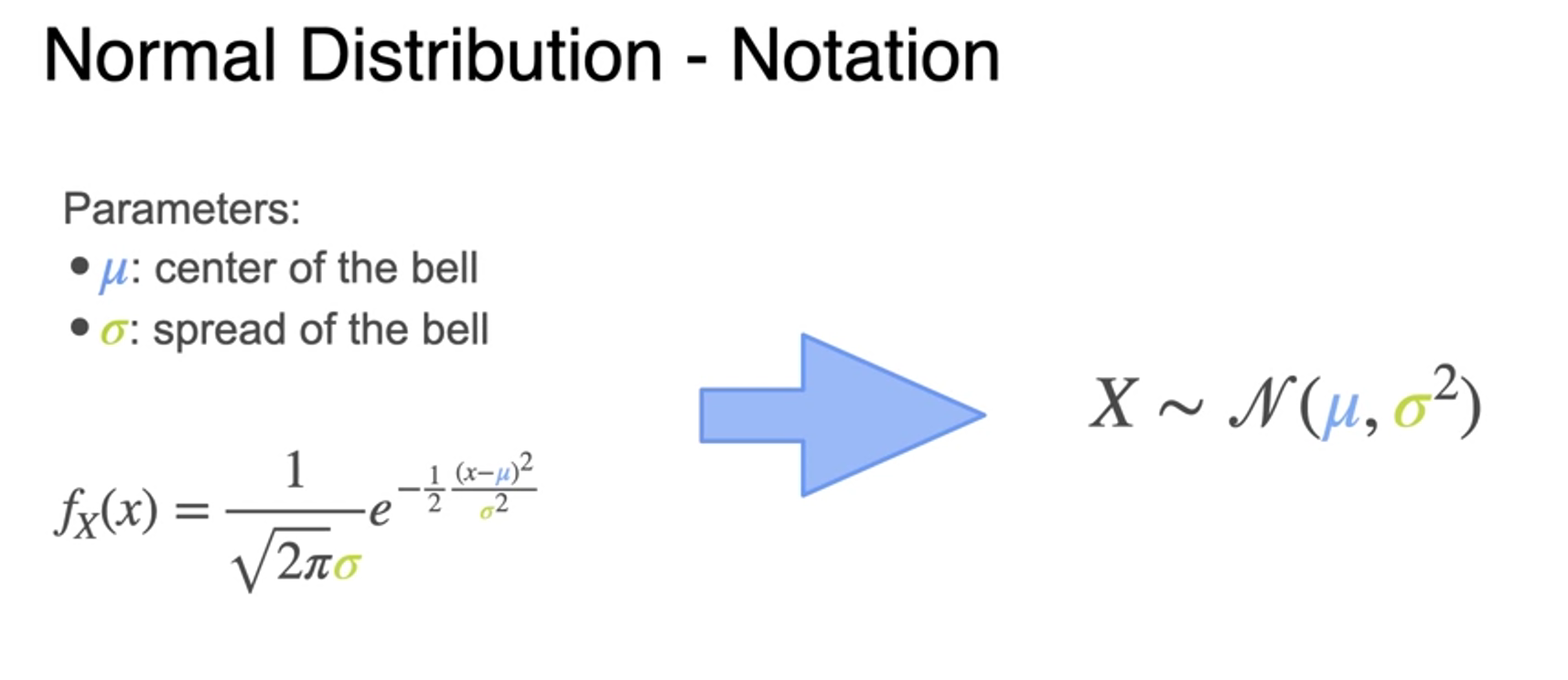
- is similar
- sigma squared called 분산variance
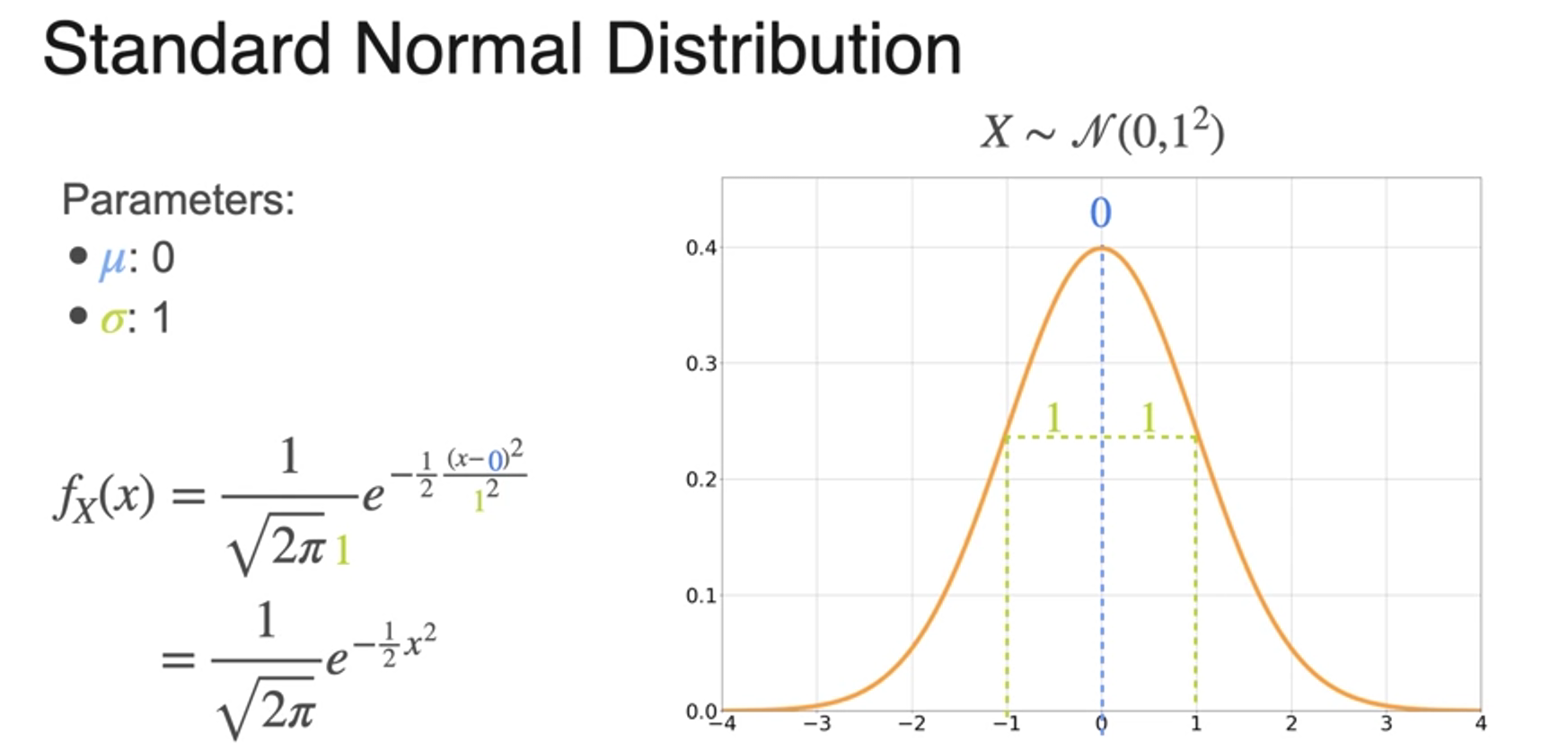
- 정규분포
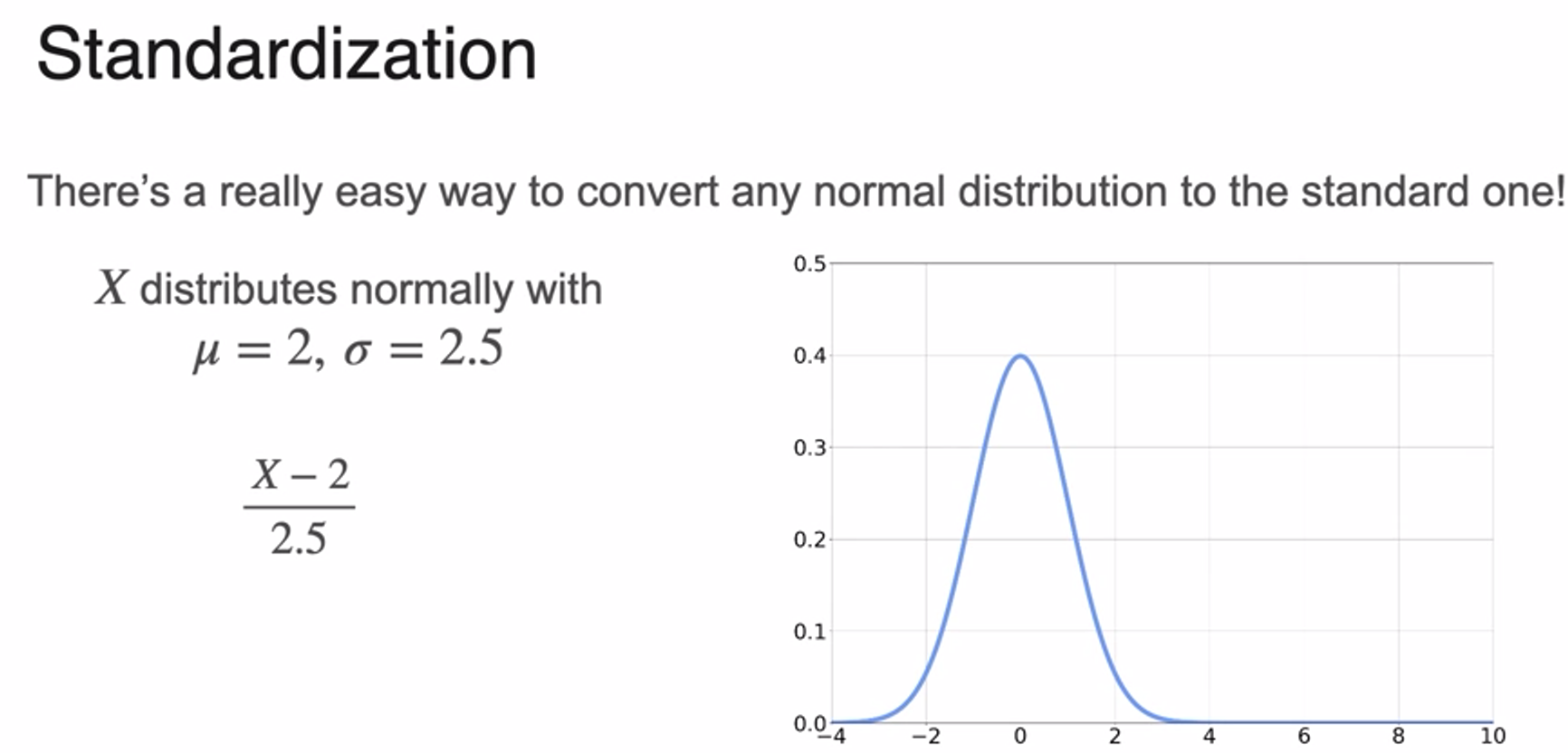
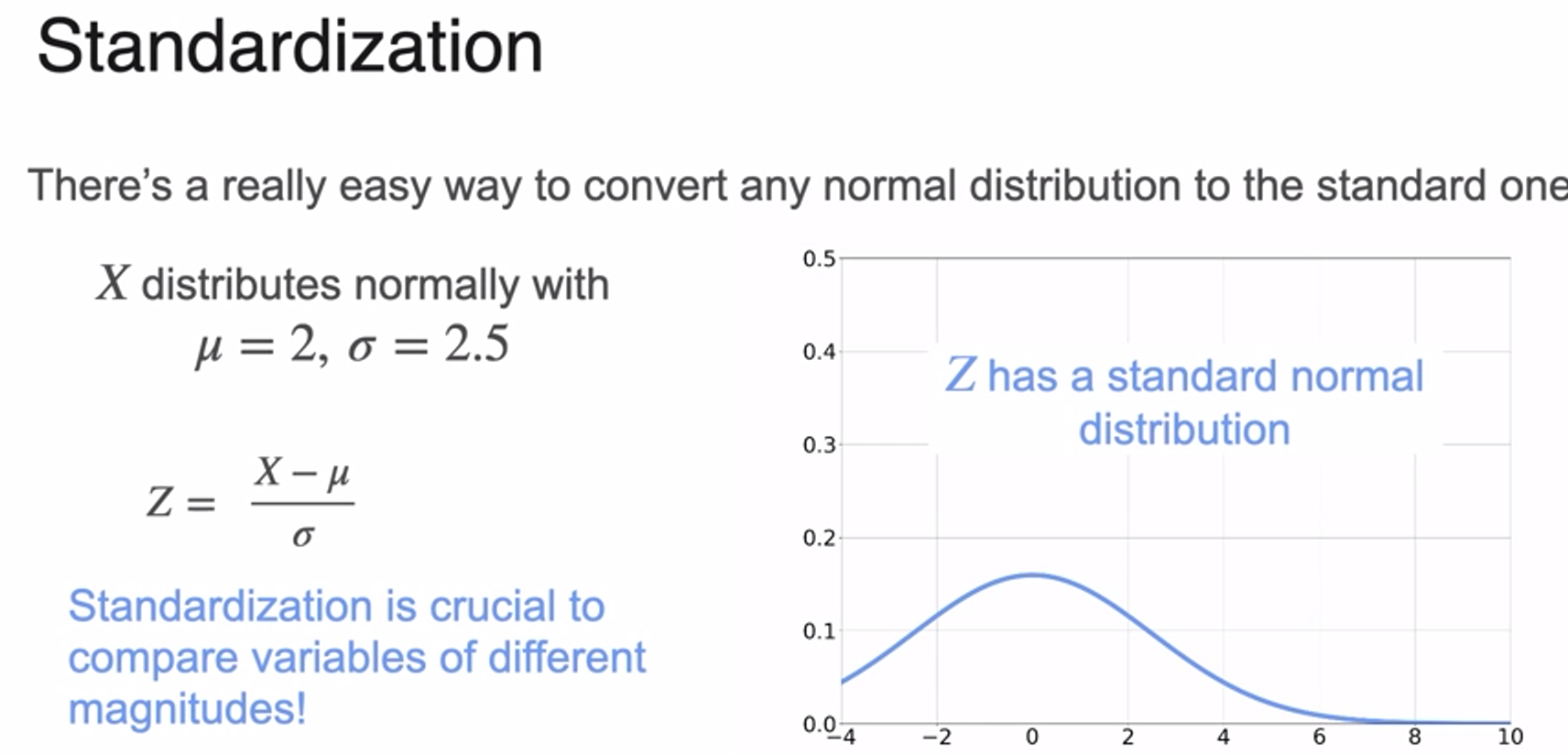
- 많은 ML에서는 변수가 정규분포를 따른다고 가정
(Optional) Chi-Squared Distribution
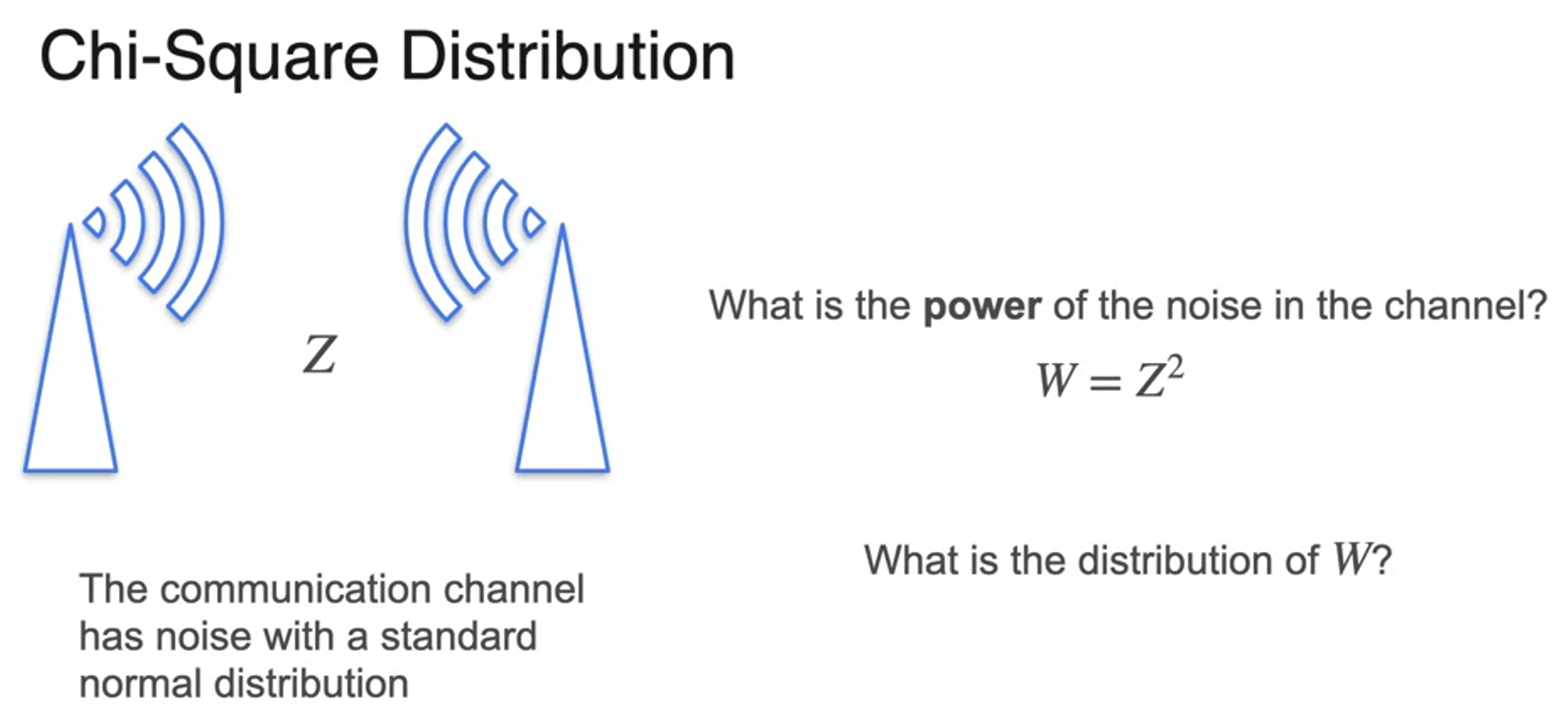
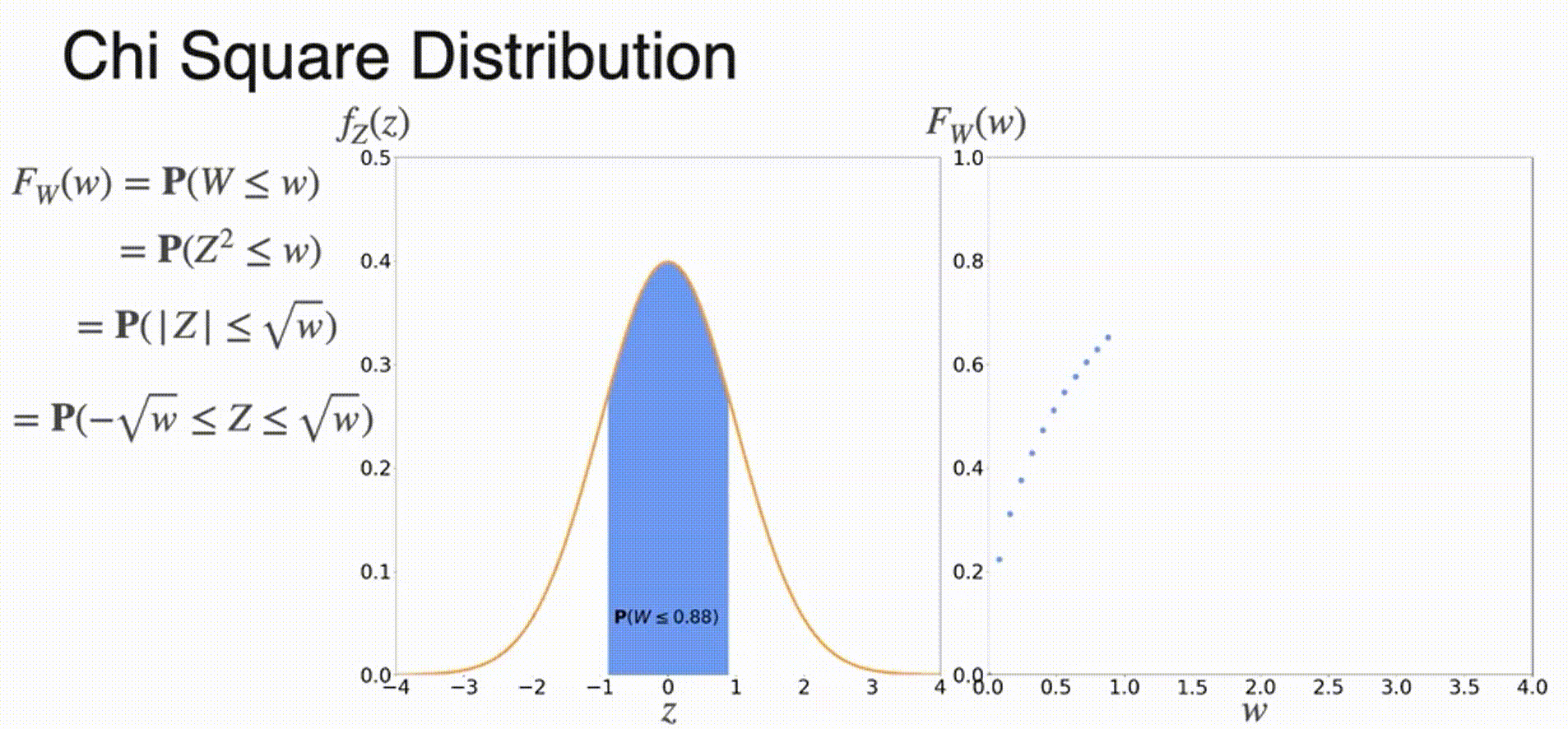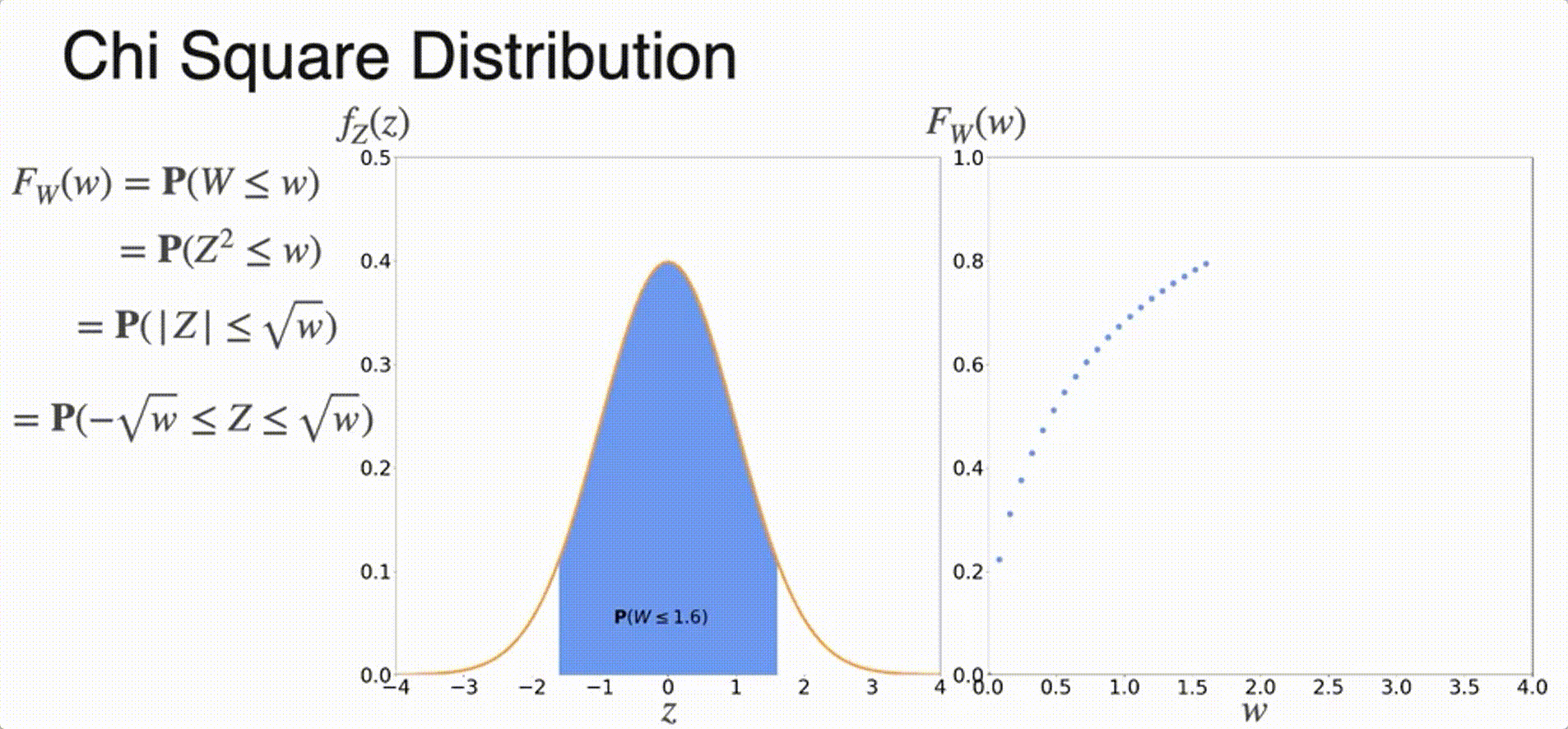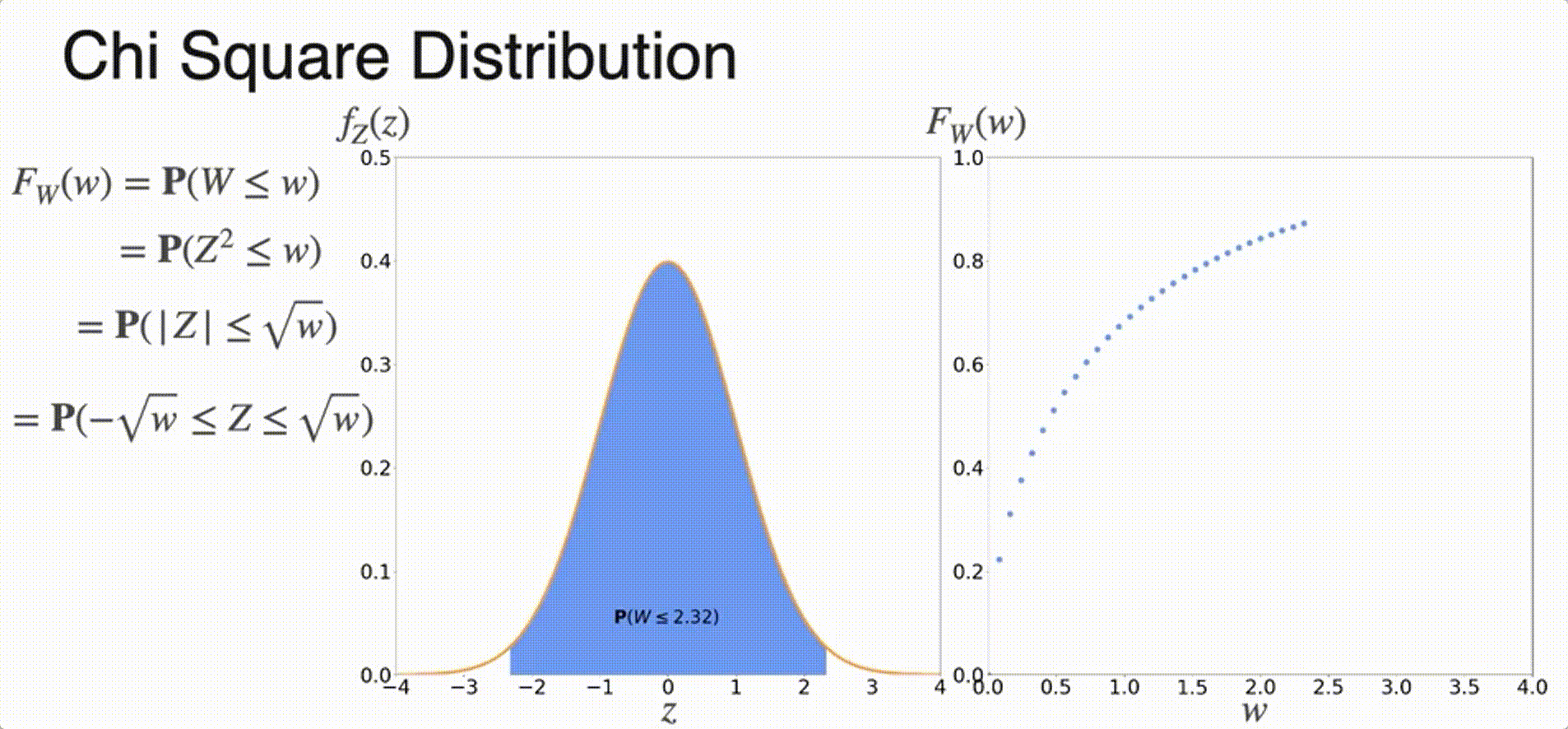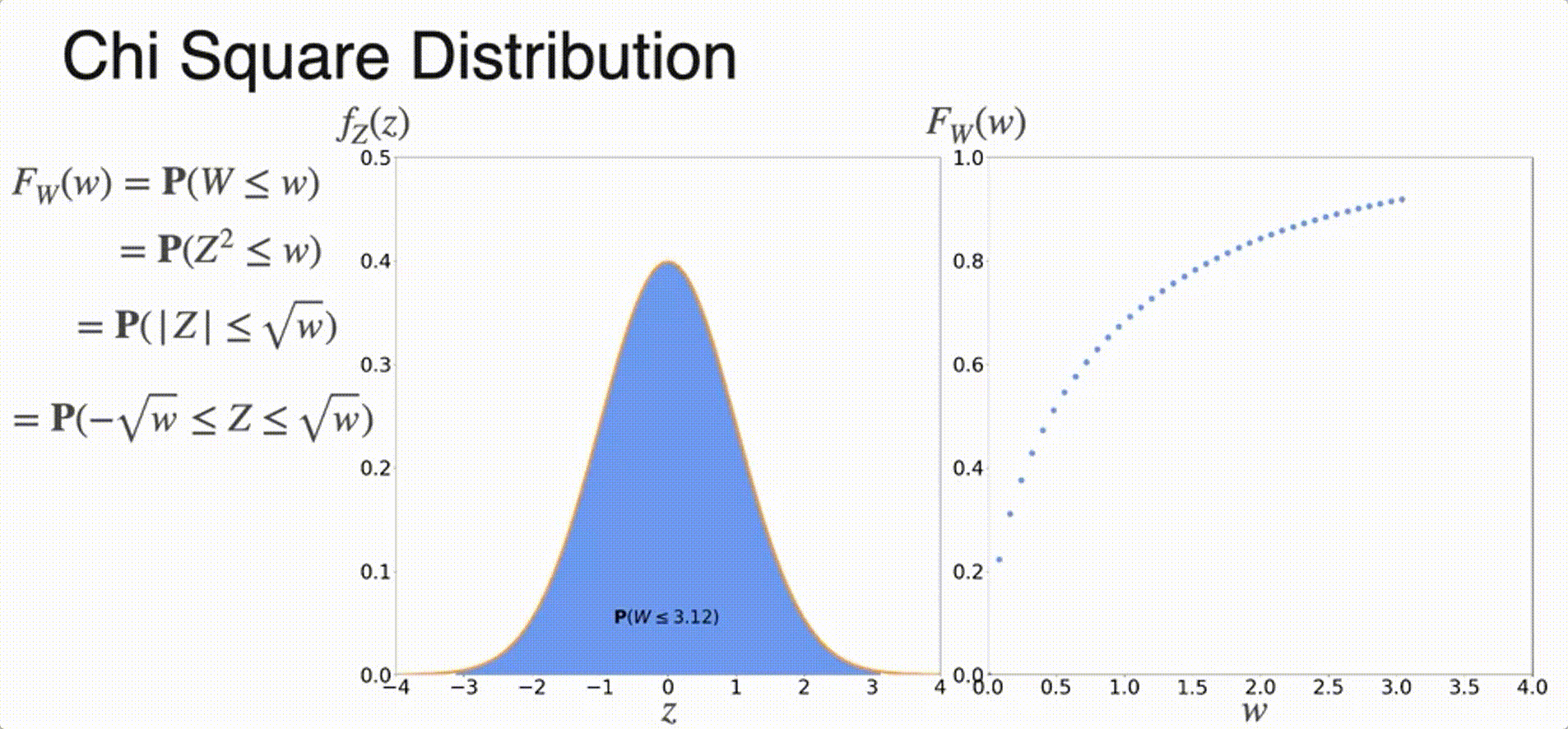
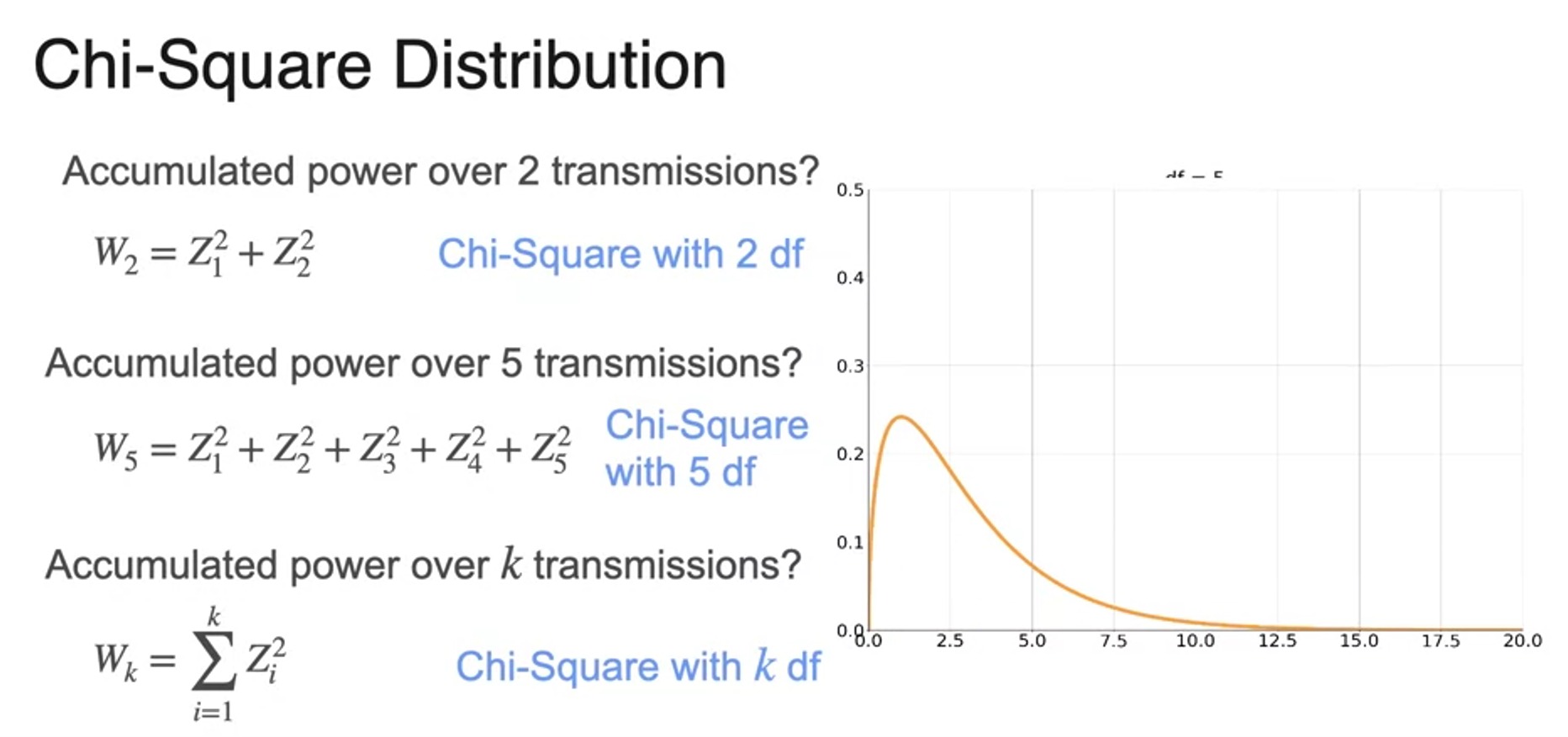
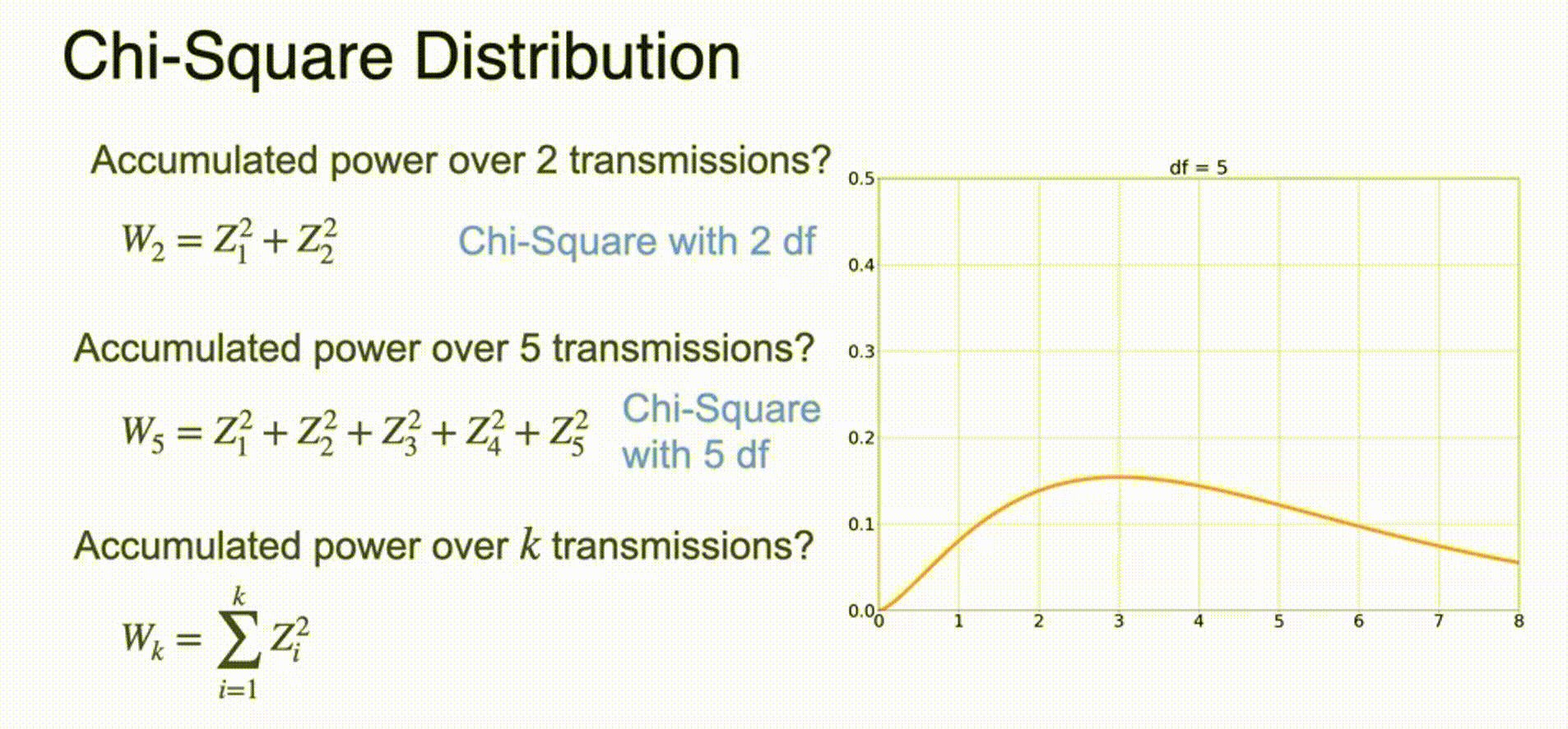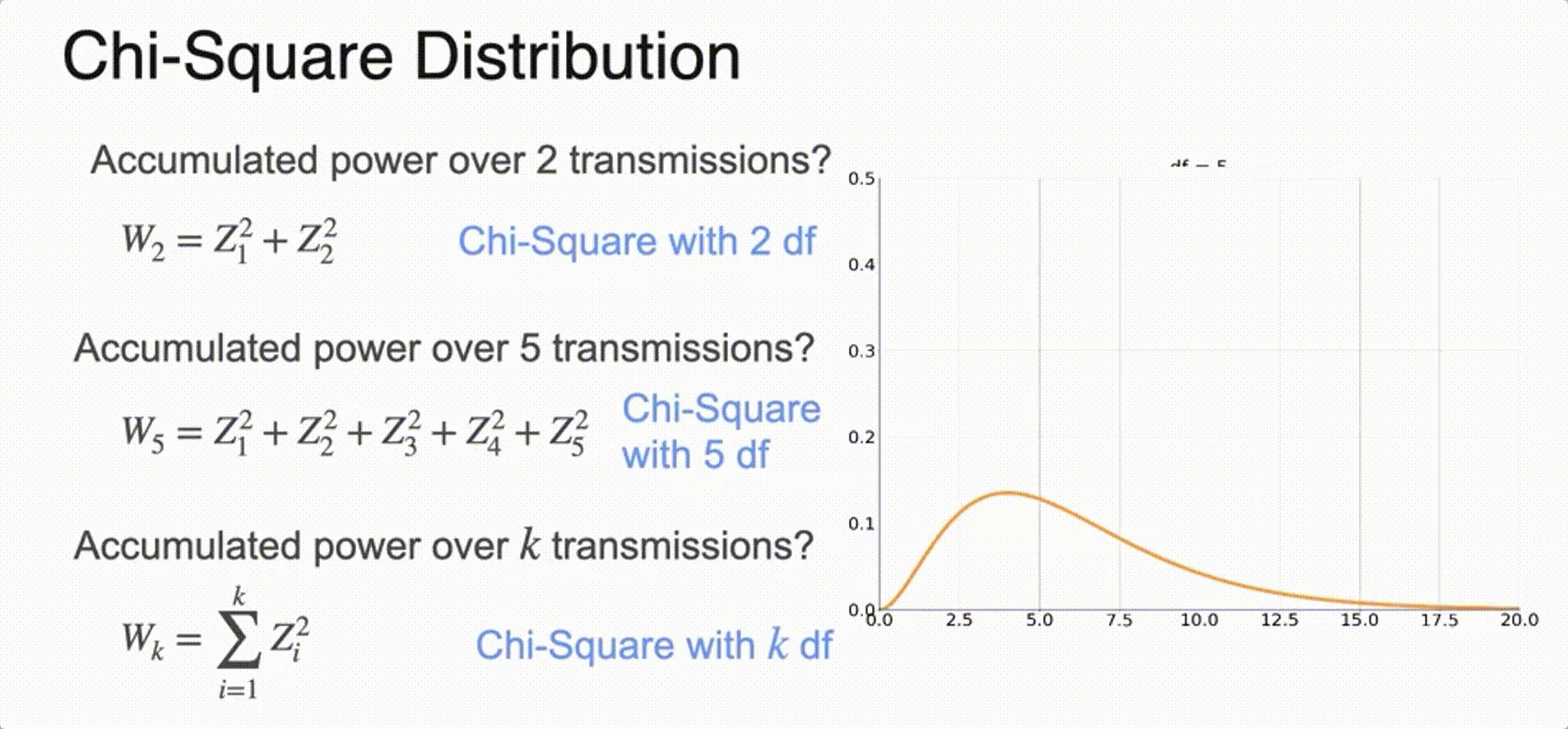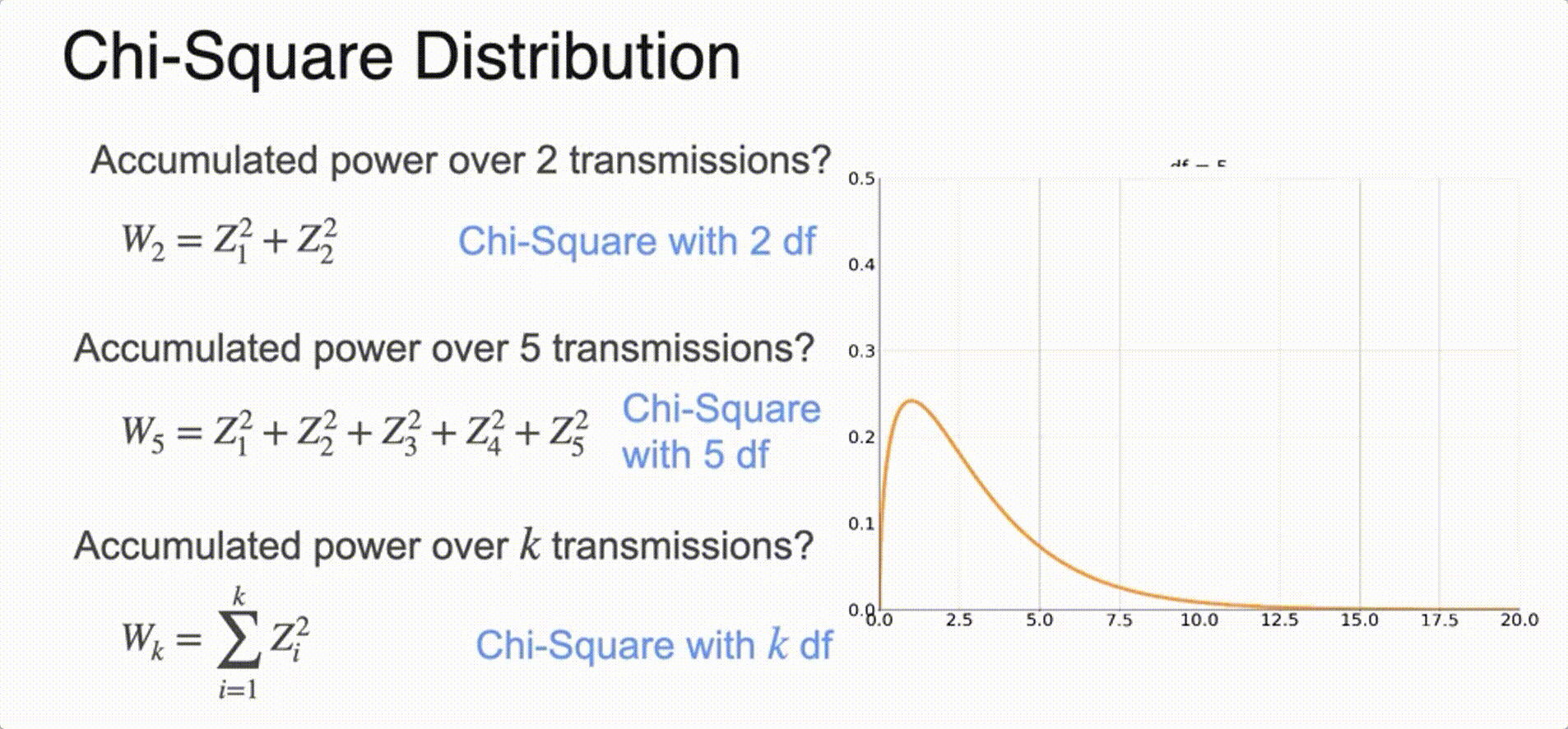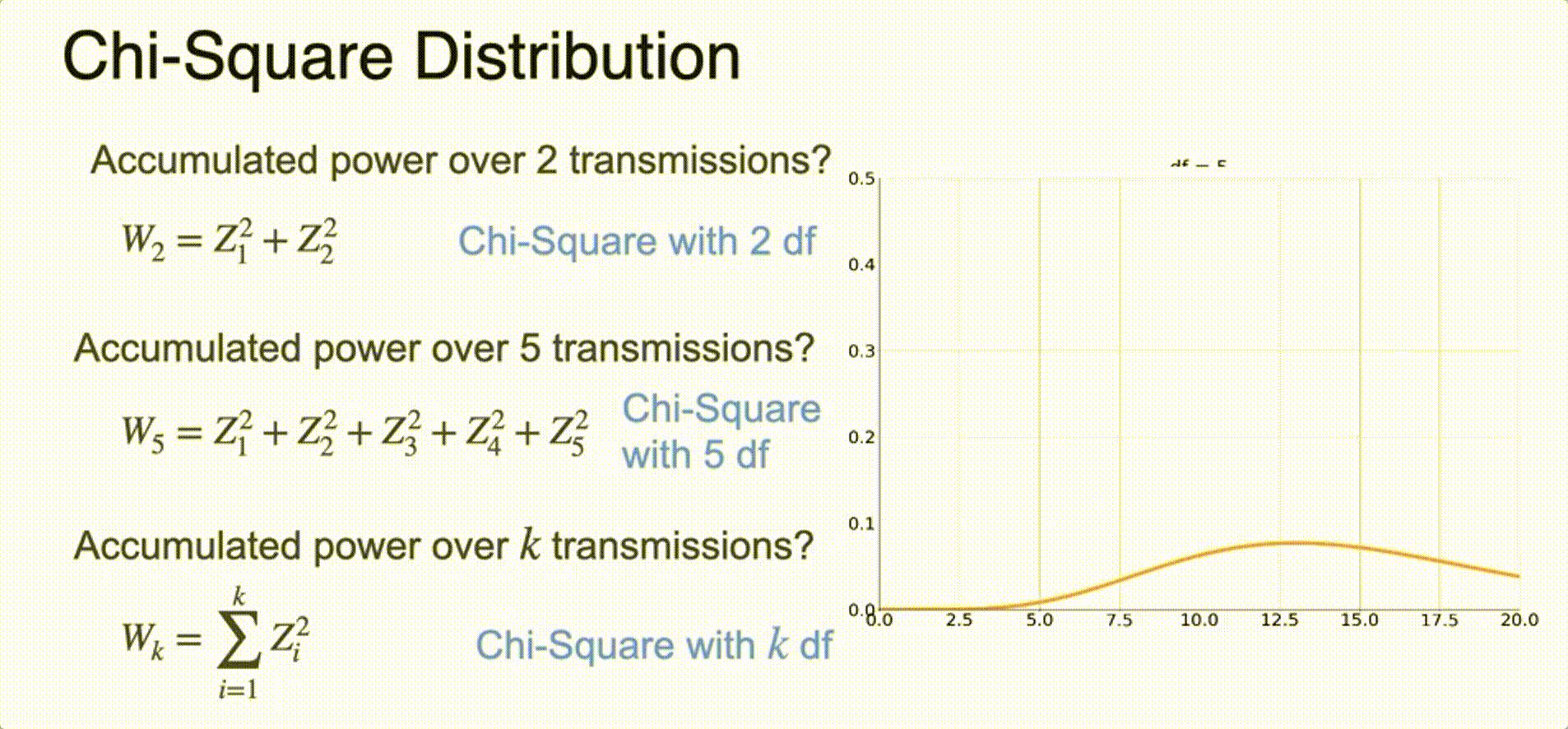
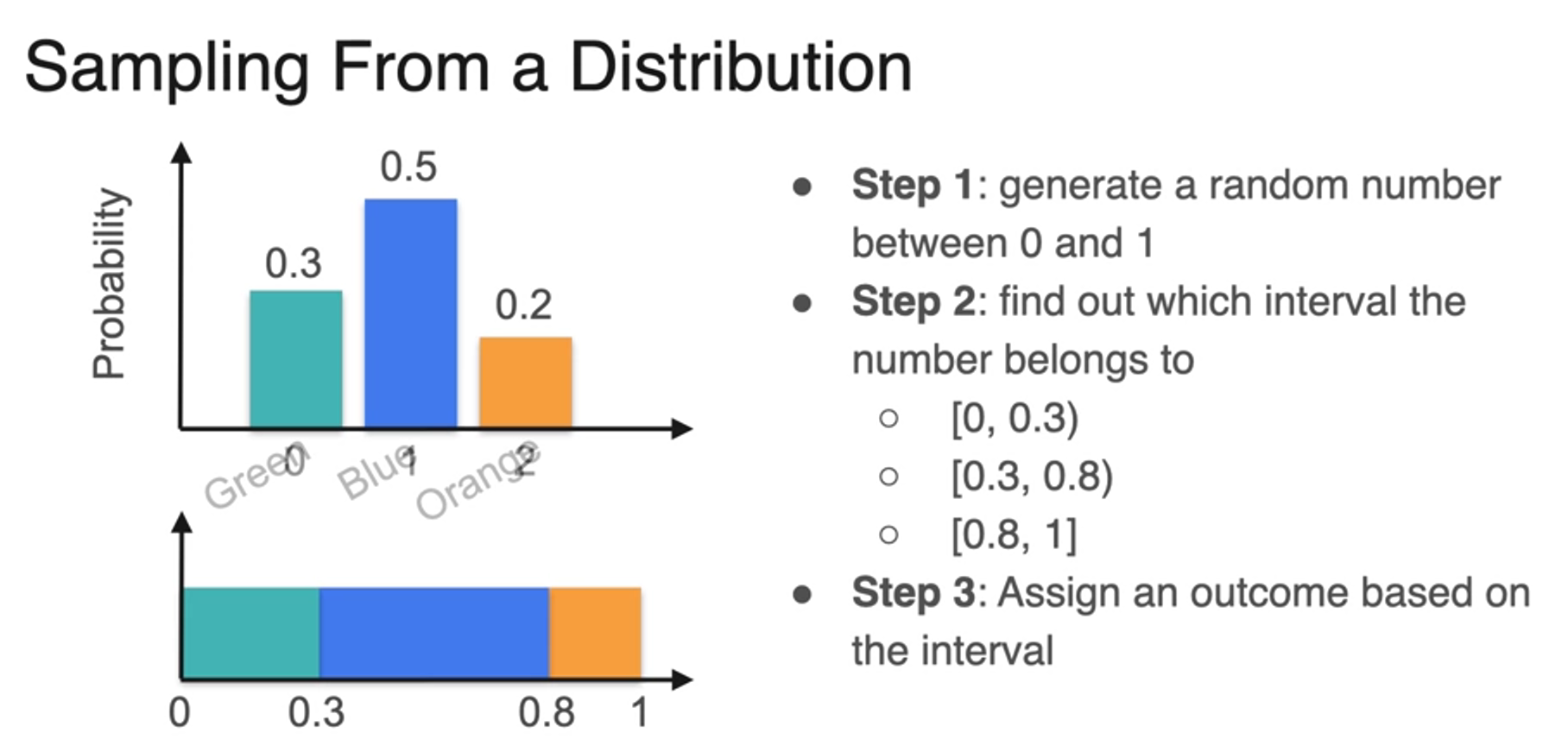
Sampling from a Distribution