RL Course by David Silver - Lecture 3: Planning by Dynamic Programming

• Breaking down overall problem to simpler pieces.
• subproblems occur many times - recursive
  • Bellman equation : how to recursive decomposition
  • VFS

-example of dynamic programming

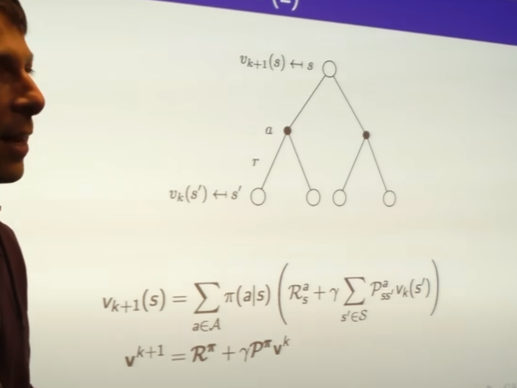
• review last lecture

Policy Evaluation

• how long it takes you to terminal state on average

• value function helps us figure out better policy

• just evaluating one policy we can use that to build new policy by acting greedily

• iterate Bellman equation and feed value back itself

Policy Iteration

• we evaluate fixed policy before

• iterate evaluate and improve until find optimal policy

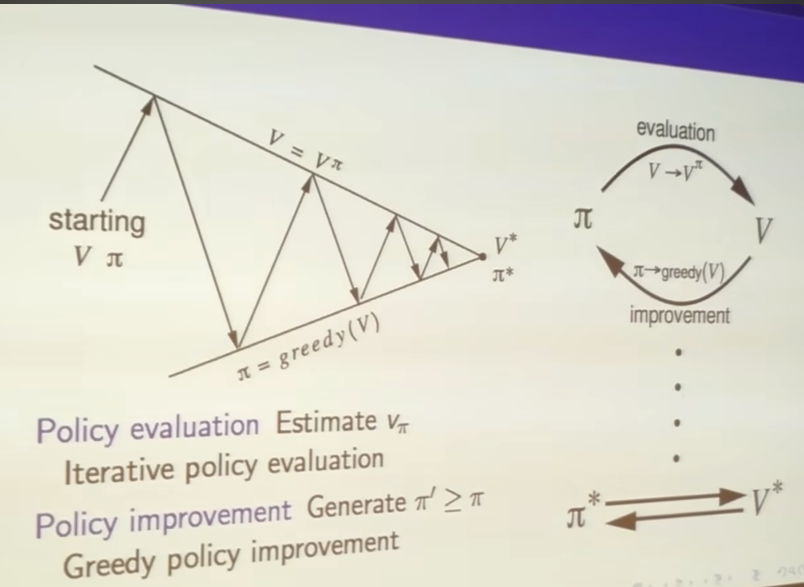
• policy evaluation up arrows, policy improvement down arrows

• no matter where you start any value function any policy
  you will always end up with
  the optimal value function, optimal policy

• contour map of policy
• number means cars we should move
• 420~612 is dollors your life time factor consider future revenue and discount factor
• even if you've got no cars in either location you'll still get money because eventually you will start getting cars coming into locations

• acting greedly always makes you deterministic

• Q : If there is no final state can we also apply dynamic PR?
  In practice the algorithm doesn't even know a final state exist. If you're in the mdp circle it goes on forever. dynamic programming still works.

• value iteration is iteration value function
  • policy iteration we constructed a value function for a particular policy; value iteration doesn't do that its more like modified policy iteration
  • value iteration doesn't build policy in the intermediate step

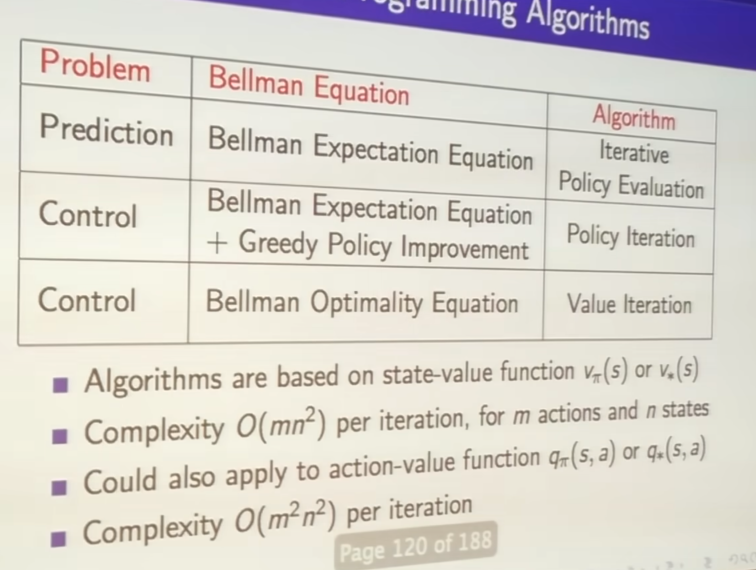
• just sweep over it

• how to reduce this too expensive procedure

• sample