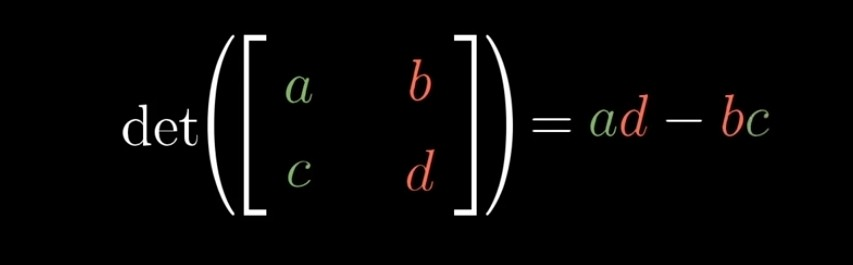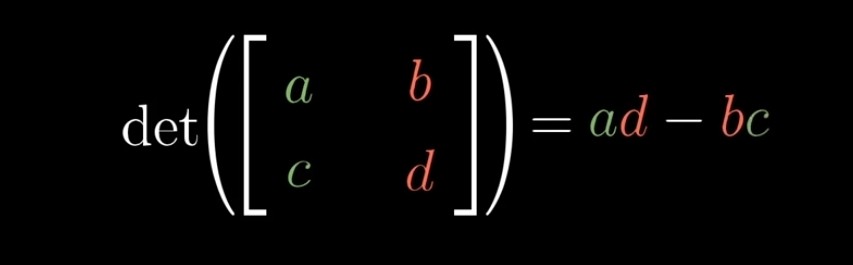
how much are areas scaled?
- 특정 지역의 크기를 증가하거나 감소시키는 팩터(factor) 값을 측정해보기
: 하나의 단위 정사각형의 영역이 얼마나 변하는지만 알면 공간 상 어떤 지역이 어떻게 별할지 예측할 수 있다.
- 크기와 상관없이 격자선이 평행하고 균등한 거리를 유지한 채 변화하기 때문이다.
determinant(행렬식)
: 정사각 행렬에 스칼라를 대응시키는 함수
the 'determinant' of a transformation
- 선형변환에 의한 영역의 변화를 나타내는 팩터
... 이해안됨
선형변환의 determinant 계산하는 방법
ex1. 한 변환의 행렬식 값이 3이라면, 특정 지역의 크기는 팩터 3만큼 증가함
ex2. 행렬식 값이 1/2라면, 영역크기를 1/2크기로 축소시키는 것을 의미함
ex3. 2차원 변환의 행렬식이 0이라면, 모든 공간이 찌부려뜨려져서 선이 될수 있음 or 한 점
→ important
how can you scale area by a negative number?
: 방향과 관계있음.
- feels like flipping space
= 변환이 마치 종이를 뒤집는 것과 같음
▶ 공간의 방향 뒤집기(orientation-flipping)
- i-hat, j-hat으로도 설명가능
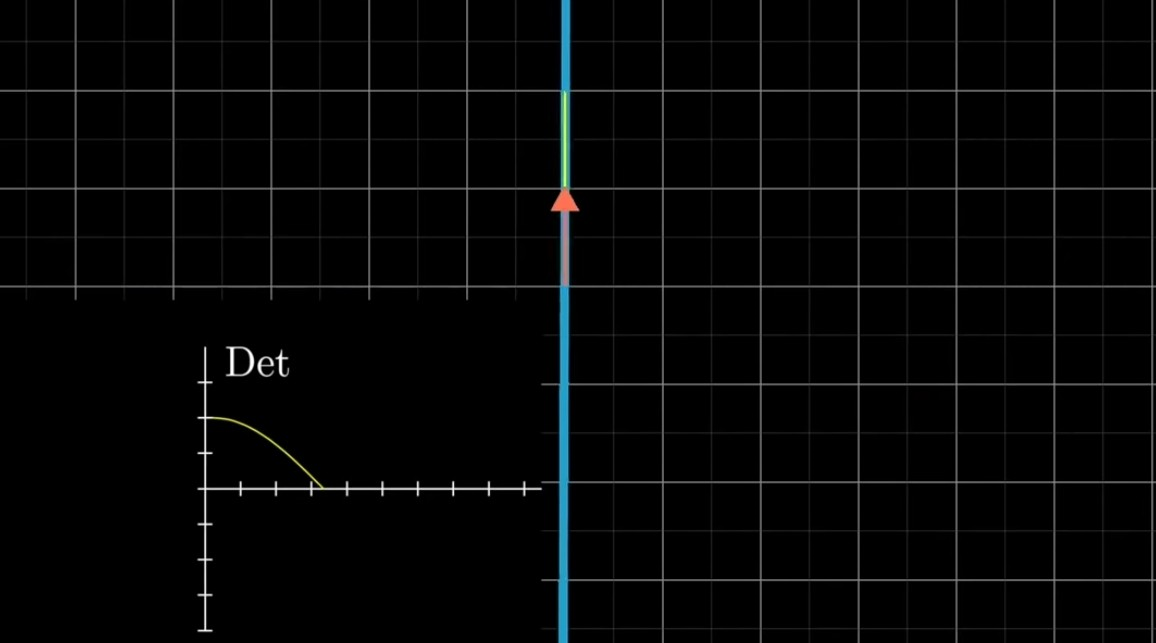
- 행렬식이 음수가 되도 여전히 영역 스케일링 관한 팩터로 볼 수 있음
: i-hat과 j-hat이 점점 가까워지면서 둘이 완전히 만나게 되면 행렬식을 0이 됨.
: 근데, i-hat이 계속 이동하게 되면 행렬식이 음수가 되는 것이 자연스럽게 됨.
3차원에서의 determinant
: 부피(volume)이 얼마나 스케일링 되는지 알려줌
- 2차원에서의 생각
- 영역크기1에 해당하는 한 정사각형을 떠올리기
- 3차원에서의 생각
- 1x1x1 정육면체 떠올리기(모서리에 각 단위벡터가 있음)
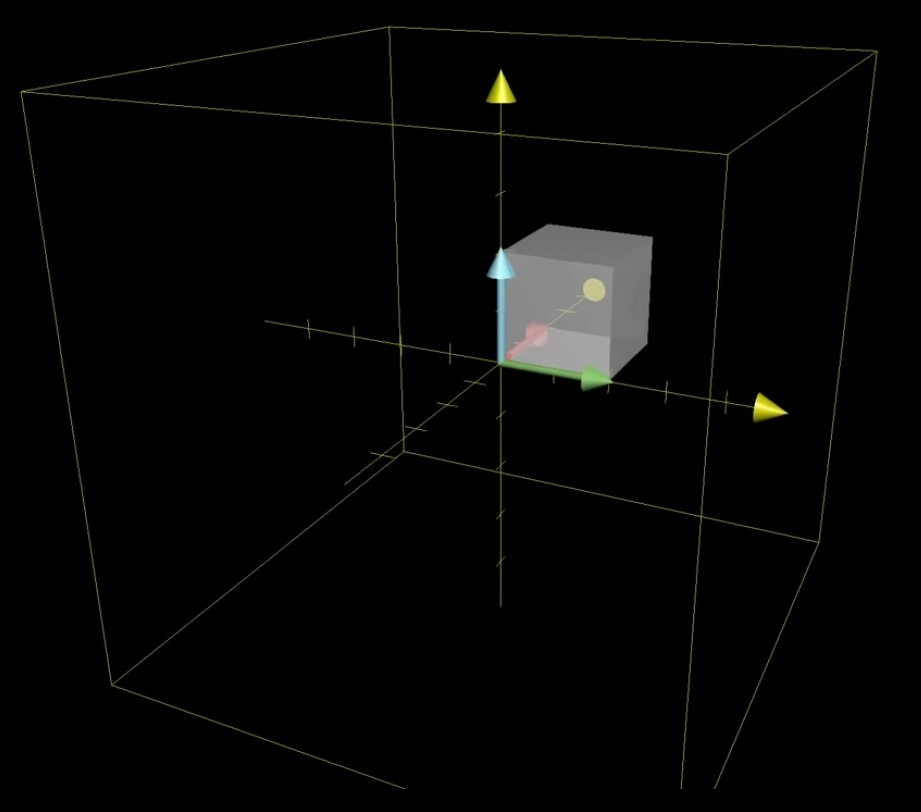
- parallelepiped: 기울어진 정육면체(평행육면체)
- 부피: 1
- 행렬식 값: 어떤 부피든지 스케일링 팩터를 알려줌
→ 평행육면체의 부피값으로 생각해도됨
- 1x1x1 정육면체 떠올리기(모서리에 각 단위벡터가 있음)
- 음수 행렬식 값의 의미
: 3차원에서의 orientation을 설명하는 방법으로 오른손 규칙 이용- 오른손 규칙이 그대로 유지될때: 양수방향
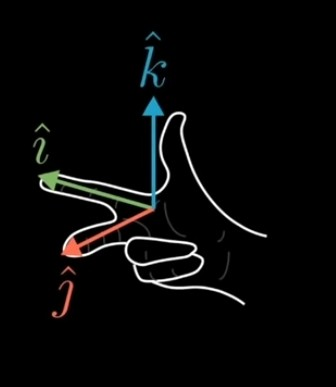
- 변환이후 왼손으로 바꿔야 하는 경우: orientation이 반전되는 경우임. 행렬식 값 음수
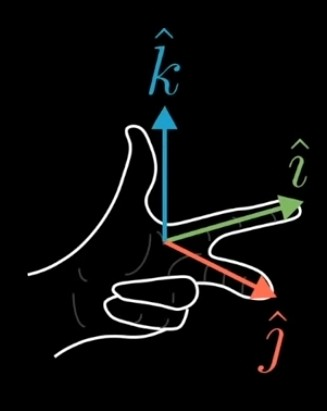
- 오른손 규칙이 그대로 유지될때: 양수방향
행렬식 계산 방법