목차
- DP란?
- 메모이제이션 (Memoization)
- 두 가지 접근법 : Top-Down, Bottom-Up
- DP를 활용하는 대표적인 문제
- 피보나치 수열
- 최적 경로 문제 - 최장 증가 부분 수열
- 최적 경로 문제 - 최장 공통 부분 수열
- 배낭 문제
DP란?
DP란 Dynamix Programming(동적 프로그래밍)의 줄임말로 복잡한 문제를 더 작은 하위 문제로 해결하는 알고리즘 설계 기법이다.
DP를 적용시키기 위해선 2가지 조건을 만족해야 한다.
최적 부분 구조(Optimal Substructure): 전체 문제의 최적해가 부분 문제의 최적해로부터 구해질 수 있어야 합니다.
예를 들어 최단 경로 문제에서 A → C의 최적 경로가 A → B → C라면, A → B까지의 최적 경로와 B → C까지의 최적 경로도 최적해여야 함.
중복되는 부분 문제(Overlapping Subproblems): 부분 문제가 중복되어 여러번 반복 계산되어야 합니다.
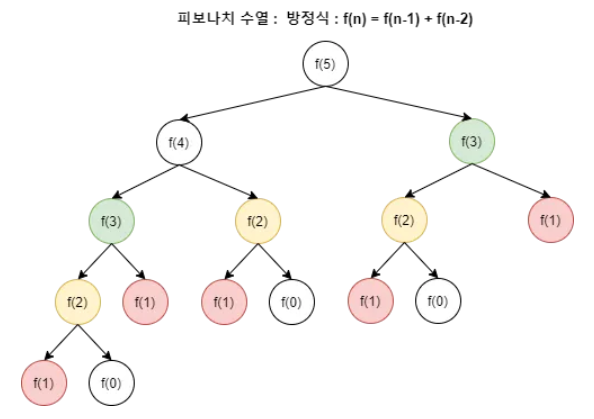
피보나치 수열에서 fib(5)를 구하려면 fib(4), fib(3)이 필요하고, fib(4)를 구하려면 fib(3), fib(2)가 필요하게 되는데, 여기서 fib(3)이 여러 번 계산된다.
메모이제이션 (Memoization)
메모이제이션은 DP의 기법 중 하나로, 이미 계산한 결과를 저장하여 중복 계산을 방지하는 기법이며, 주로 재귀(Top-Down) 방식의 DP에서 사용된다.
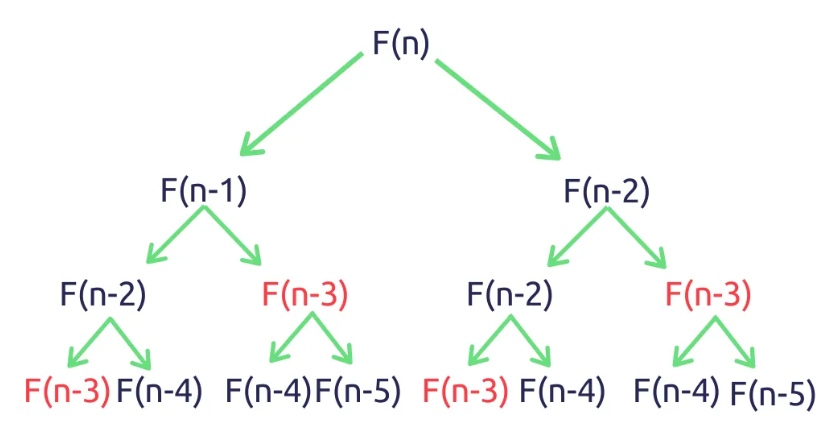
위에서 언급했던 중복되는 부분 문제(Overlapping Subproblems)를 해결하면서 속도를 개선할 수 있는 기법이다.
두 가지 접근법 : Top-Down, Bottom-Up
Top-Down
재귀 + Memoization
큰 문제를 해결할 때 작은 문제의 결과를 저장해서 다시 계산하지 않도록 하는 방식이다.
def fib_DP(n):
if n <= 0:
return -1 if n != 0 else 0
mem = [0 for _ in range(n+1)]
mem[1] = 1
for i in range(2, n+1):
mem[i] = mem[i-1] + mem[i-2]
return mem[n]Bottom-Up
반복문 사용
작은 문제부터 차근차근 해결해 나가는 방식이다.
def fib(n):
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]DP를 활용하는 대표적인 문제
피보나치 수열
n이 주어졌을 때, n번째 피보나치 수를 구하는 프로그램을 작성하시오.
위에서 언급했던 것처럼 대표적인 메모이제이션을 활용하기 좋은 문제이다.
코드는 위 Top-Down, Bottom-up 부분을 참고하면 된다.
개인적으로는 Top-Down의 형식을 선호한다.
def fib_DP(n):
if n <= 0:
return -1 if n != 0 else 0
mem = [0 for _ in range(n+1)]
mem[1] = 1
for i in range(2, n+1):
mem[i] = mem[i-1] + mem[i-2]
return mem[n]
res = fib_DP(int(input())
print(res)최적 경로 문제 - 최장 증가 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.
예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.
length라는 배열에 각 위치에서 LIS(최장 증가 부분 수열)의 길이를 저장한다.
뒤에서부터 앞으로 각 위치부터 시작하는 LIS를 구한다.
각 위치보다 뒤쪽에 있는 원소들을 하나씩 비교하면서 LIS 길이를 계산한다.
자신을 포함하는 LIS의 길이를 갱신한다.
import sys
input = sys.stdin.readline
N = int(input())
A = list(map(int, input().split()))
length = [0 for _ in range(N)]
length[N-1] = 1
for i in range(N-1,-1,-1):
for j in range(N-1, i, -1):
if A[i] < A[j]:
length[i] = max(length[i], length[j]+1)
if length[i] == 0:
length[i] = 1
print(max(length))해당 해결법은 이중 반복문을 써서 O(N^2) 가 된다.
최적 경로 문제 - 최장 공통 부분 수열
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
이 문제를 푸는 아이디어는 이렇다.
- A와 B 모두 인덱스 1부터 시작한다.
- 서로 비교했을 때 문자가 같다면 값을 1 더한 뒤 A+1, B+1을 조사한다
- 다르다면 A+1, B와 A, B+1을 조사한다.
- 이런식으로 재귀함수와 메모이제이션을 통해 최댓값을 구한다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**5)
def DF(depth, recent):
# 기저 조건: 문자열 A나 B 중 하나의 끝에 도달했을 때
if depth == len(A) or recent == len(B):
return 0
# 이미 계산한 값이 있다면 그 값을 바로 반환
if M[depth][recent] != -1:
return M[depth][recent]
# 두 문자가 같으면, 두 포인터를 모두 이동시키고 1을 더함
if A[depth] == B[recent]:
M[depth][recent] = 1 + DF(depth + 1, recent + 1)
else:
# 문자가 다르면, A에서 한 문자 넘기거나 B에서 한 문자 넘김
M[depth][recent] = max(DF(depth + 1, recent), DF(depth, recent + 1))
return M[depth][recent]
A = input().strip()
B = input().strip()
# 메모이제이션 테이블 초기화 (-1로 초기화)
M = [[-1 for _ in range(len(B))] for _ in range(len(A))]
# 재귀 함수 호출
print(DF(0, 0))배낭 문제
N개의 물건이 있다.
각 물건은 무게 W와 가치 V를 가지고, 최대 K만큼의 무게만을 넣을 수 있는 배낭이 있다.
배낭에 넣을 수 있는 물건들의 가치의 최댓값을 구하시오.
- 차례대로 물건을 조사한다.
- DP(메모이제이션 하는 배열)을 DP[i][w]라 할 때 w 부터 차근차근 채운다.
- 현재 물건 무게
L[i][0]가 배낭 용량w보다 크다면?- 넣을 수 없기 때문에 이전 상태 그대로 유지한다.
- 물건을 넣을 수 있다면?
- 아래 두 경우 중 최댓값을 선택해서 채운다
- 넣는 경우 →
DP[i-1][w - L[i][0]] + L[i][1] - 안 넣는 경우 →
DP[i-1][w]
import sys
input = sys.stdin.readline
N, K = map(int, input().split()); L = [[0,0]]; DP = [[0 for _ in range(K+1)] for i in range(N+1)]; res = 0
for i in range(N):
L.append(list(map(int, input().split())))
for i in range(1, N+1):
for w in range(K+1):
if L[i][0] > w:
DP[i][w] = DP[i-1][w]
else:
DP[i][w] = max(DP[i-1][w-L[i][0]] + L[i][1], DP[i-1][w])
print(DP[N][K])