Duke University : T-distribution

Review: What purpose does a large sample serve?

With independent observations and not extremely skewed population distribution, a large sample would ensure…

• A nearly normal sampling distribution of the mean
• A better s estimate for the population SD, sigma
• A reliable estimate of the Standard Error (s / route(n))
  • Standard Error is the standard deviation of the sampling distribution of a statistic.
  • The uncertainty of Standard Error estimate is addressed by using the T-distribution

T - distribution (1)

• Used for inference on a mean where sigma is unknown. (almost always)
• To address the uncertainty of the Standard Error estimate
• Unimodal, symmetric
• Bell shaped but thicker tails than the normal distribution
  • As s (sample standard deviation) is used instead of sigma (population standard deviation)

Normal distribution vs T – distribution

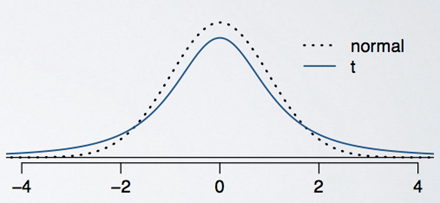
• Peek of the t-distribution is lower than that of the normal distribution, but has thicker tails
• Observations are more likely to fall beyond two standard deviations from the mean than under the normal distribution.
• Confidence intervals constructed using the t distribution will be wider, more conservative than those constructed with the normal distribution.
• Thicker tails are helpful for mitigating the effect of a less reliable estimate for the standard error of the sampling distribution

T-distribution over Standard Normal Distribution

1. Population Standard Deviation (σ) is Unknown

   • If σ is unknown, you must estimate it using the sample standard deviation (s). This introduces additional uncertainty, which the t-distribution accounts for.

2. Small Sample Size(n<30)

   • For small sample sizes (𝑛<30), the variability in the sampling distribution is greater, and the t-distribution's heavier tails adjust for this increased uncertainty.
   • The Z-distribution assumes the sample size is large enough for the Central Limit Theorem to smooth out these variations.

3. Heavier Tails in the t-Distribution

   • The t-distribution has heavier tails compared to the Z-distribution. This means it is more likely to account for extreme values or outliers, which are more impactful in small samples.

T - distribution (2)

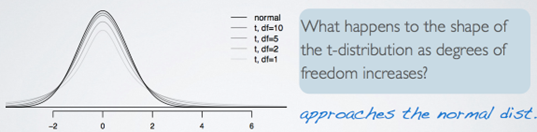
• Always centered at 0 (like the standard normal)
• Has one parameter: degrees of freedom(df) which determines the thickness of tails
  (the normal distribution has two parameters: mean and SD)
• As the degrees of freedom increases, it aproaches normal distribution.
• Degrees of freedom is tied to sample size

T Score for a Hypothesis Test

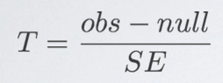
(Example)
Effect of degrees of freedom in t-distribution, significance level = 0.05

• P(|Z| > 2) = 0.0455 - reject
• P(|t df = 50| > 2) = 0.0509 – fail to reject ?
• P(|t df = 10| > 2) = 0.0734 – fail to reject

• More conservative with a t distribution with lower degrees of freedom, less likely to be able to reject the null hypothesis.
• Not as easy to reject the null hypothesis with a small sample size and stronger evidence is needed in order to be able to do so.
텍스트