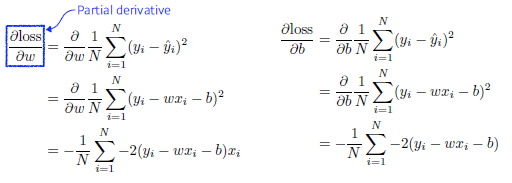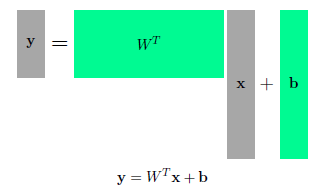Neural Networks & Multi-Layer Perceptron

공부 내용

• Neural Networks
• Linear Neural Networks
• Multi-Layer Perceptron

Neural Networks

• Neural Network는 동물의 뇌를 구성하는 생물학적 신경망에서 영감을 얻은 컴퓨팅 시스템이다.
  • 영감을 얻었을 뿐 완전히 같다고 보기는 힘들다. (ex. 비행기를 새랑 같게 만들지는 않는다.)
• Neural Network는 nonlinear transformations으로부터 발생하는 affine transformations을 쌓은 function approximator이다.

Linear Neural Networks

Gradient descent

• Data : $(x, y)$ 형태의 N개의 데이터
• Model : wx+b 식을 통한 yhat 계산
• Loss : MSE(mean square error)

• 최적화 변수 w와 b에 대해서 각각 편미분을 계산한다.

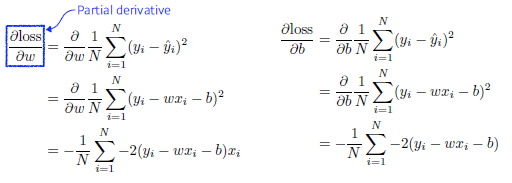
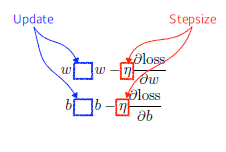
• 최적화 변수 w,b를 반복적으로 업데이트한다. (gradient descent)
  • 여기서 stepsize는 learning rate -> 적절히 조절해 줘야 한다.

다차원 input, output 다루는 법

• 다차원 input과 output 또한 다룰 수 있다.
  • 행렬 연산 활용(affine transform)

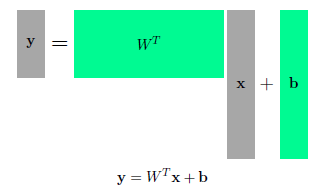
• 행렬을 두 벡터 공간 사이의 매핑으로 간주하여 행렬을 해석할 수 있다.

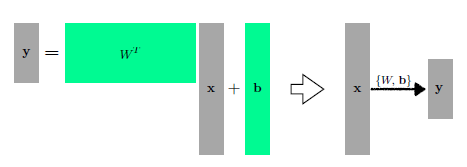
Neural Network 여러개 쌓으려면?

• 행렬을 여러 개 곱함으로서 Neural Networks를 쌓을 수 있다.

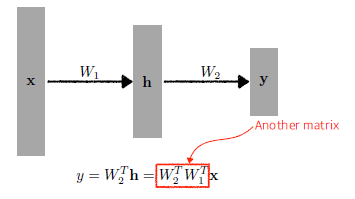
• 하지만 단순히 곱하기만 하면 1층을 쌓았을 때와 다를 게 없다.
  -> 중간에 nonlinear transform(activation function)을 넣어줘야 한다.

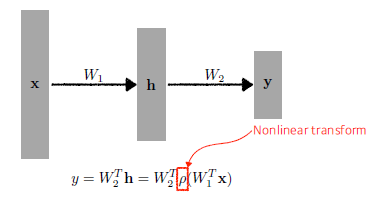
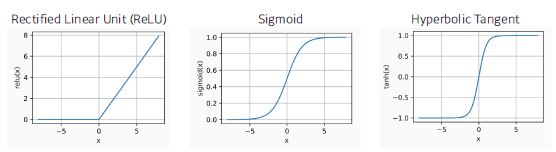
Activation Function

• ReLU
• Sigmoid
• Hyperbolic Tangent

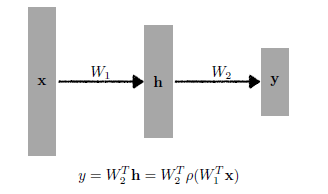
Multi-Layer Perceptron

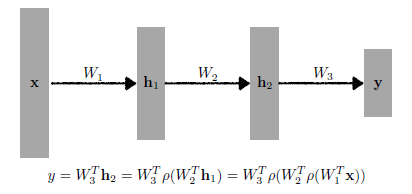
• 아래와 같이 여러 개의 Neural Layer 계층을 쌓은 구조를 다층 퍼셉트론(Multi-Layer Perceptron)이라고 한다.

• 다음과 같이 더 깊게 쌓을 수도 있다.

loss function

• Regression Task : MSE
  • True target과 Predicted output의 차이를 계산
• Classification Task : CE(Cross Entropy)
  • 해당 output의 값 중 제일 큰 숫자가 들어간 출력의 index만의 고려
    -> 다른 값들 대비 높기만 하면 된다.
• Probabilistic Task : MLE(Maximum Likelihood Estimation)
  • 단순히 output만 맞추는 게 아니라 uncertainty 정보까지 찾고 싶을 때 활용