What is the normal equaton?

• 정규 방정식(normal equation)은 최소제곱 문제(Least Squares Problem)에서 사용되는 방법으로, 선형 회귀에서 모델 파라미터를 추정하는데 사용되는 주요한 방법입니다.

-> 주어진 데이터 포인트들과 모델의 예측 값 사이의 오차를 최소화하여 모델의 파라미터를 추정하는 것이 목표입니다.
-> 정규 방정식은 최소제곱법(Ordinary Least Squares)을 수학적으로 해결하는 방법 중 하나라고 말할 수 있습니다.

간단하게 정리하자면, 정규 방정식은 다항 방정식을 행렬로 나타내고, 역행렬을 통해 최적의 값을 찾는 방법이라고 말할 수 있습니다.

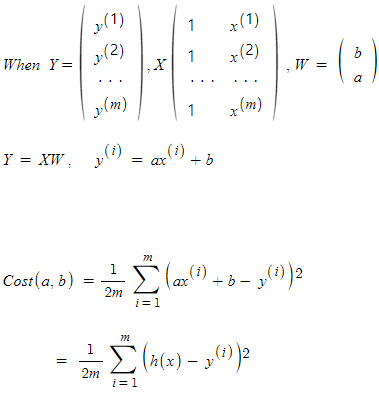
위와 같이 정규 방정식에서 비용 함수는 주로 평균 제곱 오차(Mean Squared Error, MSE)를 사용합니다.
위 수식의 비용 함수에서 제곱을 사용하는 이유는 오차의 크기와 오차의 제곱을 통한 평가 및 최적화를 효과적으로 수행하기 위함입니다. 1/2m을 곱해준 이유는 미분을 편라하게 하기 위한 목적으로 사용됩니다.

최솟값을 찾을 때, 주로 미분을 사용하는데 이처럼 정규 방정식에서도
a, b에 대한 최솟값을 찾기 위해 각 변수에 대해 편미분을 취해줍니다.

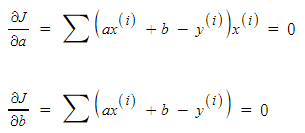
최적의 계수 a, b를 구하기 위해 아래와 같이 역행렬을 이용하여 값을 찾기 위한 식을 정리해볼 수 있습니다.

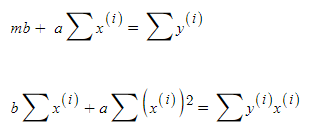
이를 행렬로 나타내면 아래와 같습니다.

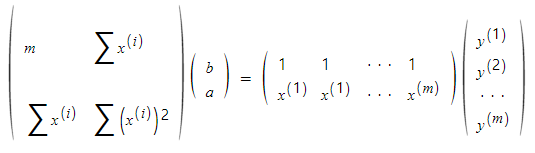
식을 간단히 나타내면 아래와 같고, cost값을 최소로 하는 a, b를 구할 수 있습니다.

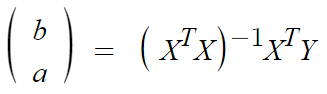
선형 회귀(Linear regression)

정규 방정식이 선형회귀에서 모델 파라미터를 추정하는데 쓰이는 방법이기 때문에 선형 회귀에 대해서도 알아보겠습니다.

먼저, x:[1, 2, 3]이라는 어떠한 입력이 있을 때, 그 예측값이 각각 y:[3, 5, 7]인 것을 아는 상황이라고 가정해보겠습니다.

이때, x=4라면 y가 어떤 값을 가질까요?

우리는 y를 x에 대한 함수로 나타낼 수 있습니다. 쉽게 f(x)=2x+1이라고 유추가 가능합니다. 만약, 데이터의 개수가 매우 많아지고 복잡해진다면 머리로 풀기에는 매우 어려운 문제가 됩니다. 이렇게 어려운 문제는 컴퓨터에게 대신 계산해달라고 할 수 있습니다.

컴퓨터는 문제를 어떻게 풀 수 있을까요?
이러한 문제를 선형 회귀(Linear regression)이라고 합니다.
선형 회귀 문제를 풀 수 있게 되면, 새로운 입력이 들어와도 y값을 유추해낼 수 있습니다.

선형회귀는 실제로 다양한 사례에서 매우 많이 관측되고 사용됩니다. 그렇기 때문에 굉장히 실용적인 모델이라고 할 수 있으며, 머신러닝과 통계에서 가장 기본이 되는 알고리즘이라고 할 수 있습니다.

이제, 컴퓨터가 선형 회귀 문제를 풀 수 있도록 해보겠습니다.

가장 먼저, 가설을 세워야 합니다.
가설함수는 H(W, b)=Wx+b라고 할 수 있고, 위 상황에서는 인간은 W는 2, b는 1이라고 유추할 수 있습니다.

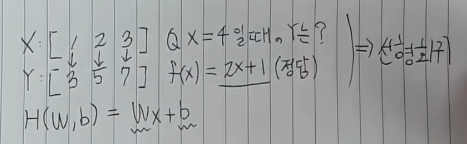
하지만, 컴퓨터는 인간처럼 유추를 할 수 없고 컴퓨터를 인간처럼 학습을 시켜줘야 하는 것 입니다.

다시 말해, 우리의 목표는 W값과 b값이 있을 때, W=2, b=1으로 만드는 것입니다.
컴퓨터는 이를 모르는 상황이기 때문에 가설을 초기화하여, 임의로 W=1, b=0이라고 가정해보겠습니다. 반복적인 연산을 통해서 현재 1인 W와 0인 b를 목표와 가깝게 학습을 시켜야 합니다. 이를 위해서는 현재 가설이 목표와 얼마나 잘못되었는지를 판단하기 위한 척도가 필요합니다.

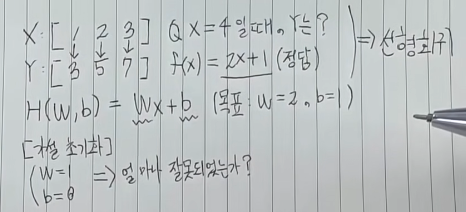
일반적으로, 이를 cost라고 합니다.->cost(W, b)
주로 최소제곱법을 이용하여 구합니다.

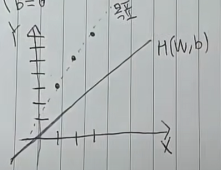
다시 돌아가서, 가지고 있는 x:[1, 2, 3], y:[3, 5, 7]을 그래프로 나타내보면 이와 같습니다.

이때 우리가 임의로 세운 가설인 W=1, b=0을 그래프에 그려보면 이와 같습니다.

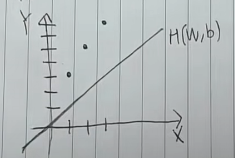
우리의 목표는 원래의 데이터와 가깝게 H(W, b)를 옮겨주는 것입니다.

원래의 데이터와 가깝게 옮겨주기 위해서 '얼마나 잘못되었는가'를 판단하기 위해 비용함수를 정의해준 것 입니다.

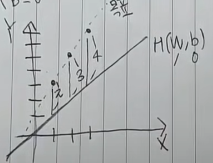
최소제곱법은 원래의 값과 차이나는 정도를 제곱하여 그 값을 더해준 뒤에 데이터의 개수로 나눠주는 것입니다.

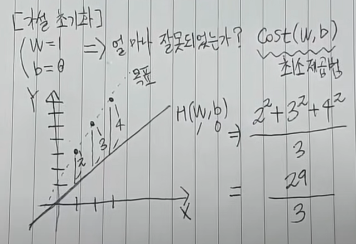
위 이미지에서의 비용은 현재 29/3로 원래의 값과 많이 차이난다는 것을 알 수 있습니다. 따라서, 현재의 값이 원래의 값에 근사하게 되면 이 비용은 0과 가까워지게 됩니다.

우리는 이 비용 함수를 정의할 수 있는데,

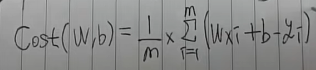
위 수식처럼 나타낼 수 있습니다.
여기서 Wxi+1은 우리가 설정한 가설 즉, 예측값이라고 할 수 있고 yi는 실제값이라고 할 수 있습니다.

예측값과 실제값의 차이는 항상 양수로 나와야하기 때문에 제곱을 사용하였습니다. 양수로 만들기 위해서는 제곱 외에도 절댓값으로도 나타낼 수 있는데 왜 하필 제곱을 사용했을까요?

이에 대해서는 두가지 이유가 있습니다.

-> 제곱을 이용하면 비용이 더 커지기 때문에 가설이 잘못되었을 때 그에대한 패널티를 더 크게 부여하기 위해서 입니다.
-> 컴퓨터가 절댓값을 계산하기 위해서는 조건문을 이용해야하기 때문에 연산속도가 더 느려질 수도 있기 때문입니다.

그렇다면, 우리는 이 비용을 어떻게 줄여나갈 수 있을까요?

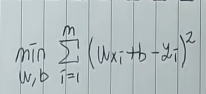
비용을 줄여나가기 위해서 값을 최소화하는 W, b값을 찾아야 합니다.

W는 식에서 기울기를 나타내는데, 만약 W를 잘못 설정하게 된다면 오차는 기하급수적으로 늘어나게 됩니다.
이를 표현하기 위해서, x축을 W로 y축을 cost로 설정하겠습니다.우리가 궁극적으로 찾고자하는 W의 값 즉, global optimum이 있다고 가정합니다.

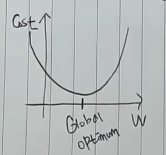
W의 값이 global optimum과 멀어지게 되면 비용은 증가하기 때문에 위처럼 이차함수 그래프로 나타낼 수 있습니다.

기울기가 0이 될 때, global optimum이기 때문에
기울기가 음수라면, 오른쪽으로 (+) 옮겨가고,
기울기가 양수라면, 왼쪽으로 (-) 옮겨가면 됩니다.
옮기는 과정을 반복해서 global optimum을 찾아 나가면 됩니다. 이러한 방법을 '경사하강법(Gradient Descent)라고 합니다.

쉽게 말해, 경사하강법은 cost를 줄이기 위해 반복적으로 기울기를 계산하여 변수의 값을 변경해나가는 과정이라고 할 수 있습니다.

b값은 위의 그래프에서 y절편을 말하고, W와 마찬가지로 이차함수로 나타낼 수 있습니다.

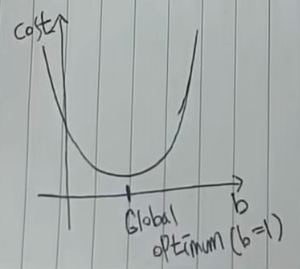
b도 같은 방식으로 위 이차함수의 기울기를 옮겨가며 최적의 값을 찾을 수 있습니다.
W와 b의 적절한 값을 찾아서 비용을 줄여나가는 과정을 선형회귀 문제를 풀어나가는 과정이라고 할 수 있습니다.

정규방정식? Gradient Descent?

정규방정식은 비용 함수를 최소화하기 위해 수학적인 방정식을 사용하는데, 이 방법은 작은 데이터셋에서 효과적이며, 계산적으로 비용이 크지 않은 경우에 사용됩니다. 하지만, 정규방정식은 역행렬이 존재해야 하는 제약이 있습니다.

경사하강법은 비용 함수를 최소화하기 위해서 비용 함수의 미분을 계산하고, 이를 이용하여 모델 파라미터를 업데이트합니다.

reference)
https://www.youtube.com/watch?v=ve6gtpZV83E