모델 선정
머신 러닝의 트리 기반 알고리즘과 딥러닝 기반의 시계열 예측 모델을 시도했다. 다음은 해커톤 기간 내에 시도했던 방법들이다.
1. 연도별 다른 데이터간의 패턴분석
모델
- Random Forest
데이터 전처리
데이터셋에서 NaN값의 분포를 분석한 결과, 데이터셋이 특정 일자를 기준으로 데이터가 채워져 있는 컬럼이 분명하게 나뉘었다. 데이터셋을 두개로 분리한 후 각각의 컬럼을 분석하니 다음과 같이 condition과 cost의 관계를 찾아낼 수 있었다.
- 2017 - 2019 : condition
- 2022 : cost
condition_df 와 cost_df 의 각각의 변수들로 '누적 생산량'의 최대화와 ‘에너지 비용’의 최소화를 추구를 목표로 했다.
- condition_df를 이용한 '누적 생산량' 예측 모델 학습:
condition_df를 입력 변수로, '누적 생산량'을 목표 변수로 하여 모델을 학습
- cost_df를 이용한 '누적 생산량' 예측 모델 학습:
cost_df를 입력 변수로, '누적 생산량'을 목표 변수로 하여 모델을 학습
- 트레이드오프 분석:
- 두 모델의 예측을 조합하여, 어떤 조건에서
condition_df와cost_df의 트레이드오프가 발생하는지 확인
- 두 모델의 예측을 조합하여, 어떤 조건에서
- ‘에너지 비용’ 최소화 & '누적 생산량' 최대화 모델:
condition_df와cost_df를 동시에 사용하여 '누적 생산량'을 최대화하면서 ‘에너지 비용’을 최소화하는 모델 구축
두 모델 간의 트레이드 오프를 분석하고 ‘에너지 비용’ 최소화와 '누적 생산량' 최대화를 위해 두 모델을 연결하는 부분에서 한계를 느껴 해당 방법을 쓰지 않기로 했다.
2. 딥러닝을 이용한 시계열 예측 모델 사용
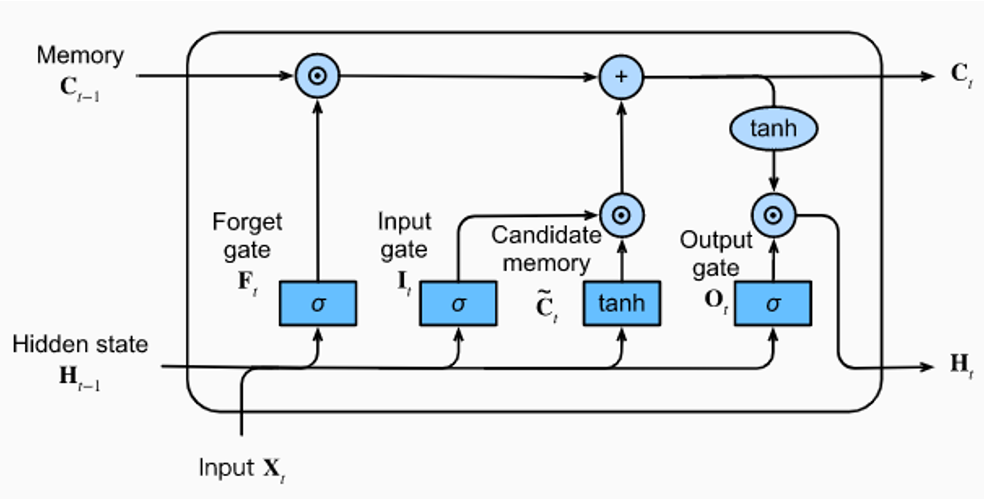
모델
- RNN
- LSTM
당시 참고했던 사이트
위 사이트는 주식 데이터를 시계열으로 예측하는데, 유사한 테스크라고 판단하여 많은 부분 참고했다.
데이터 전처리
정식일 이후 “16주” 동안 단위 면적당 최소 에너지 비용(누적 난방용 도시가스 사용량)으로 최대 수확량을 예측하는것이 목표이기 때문에, window size를 16주로 설정하고 window size 내부의 데이터별로 스케일링을 진행하는 방식으로 진행했다.
스케일링 이전에, 주어진 데이터셋에 NaN값은 없었지만, 0으로 구성된 데이터가 상당수를 차지했다.
- 실제로 0으로 측정된 경우
- NaN인 데이터가 0으로 표현되어있는 경우
두가지가 혼재하는 있는 경우, 모델의 학습에 혼란을 줄 수 있다고 생각해 위에서 언급한대로 데이터셋을 두개로 분리해서 데이터 전처리를 진행했다.
-
보간법
- 결측치 주위의 값들을 활용하여 결측치를 보간하는 방법이다.
- 정규분포를 따르지 않고 결측치 비율이 높을때 + 시계열적인 요소가 중요하다고 판단한 특성에 한해서 보간법을 적용했다.
# 특정 열들의 결측치를 주위 값들을 활용하여 보간 columns_to_interpolate = ['특정열1', '특정열2', '특정열3'] # 보간하려는 열들의 이름 리스트 # 모든 열에 대한 보간 수행 for column in columns_to_interpolate: interpolate_column = X_condition[column] X_condition[column] = interpolate_column.interpolate(method='linear', limit_direction='both')
-
K-최근접 이웃 대체 (K-Nearest Neighbors Imputation):
-
sklearn.impute.KNNImputer를 사용하여 NaN 값을 해당 데이터 포인트와 가장 가까운 이웃들의 값으로 대체했다. -
데이터가 정규분포를 따르고 결측치의 비율이 1/7 정도인 특성에 적용했다.
import numpy as np from sklearn.impute import KNNImputer # 0인 값을 NaN으로 대체 df.replace(0, np.nan, inplace=True) # K-최근접 이웃 대체 imputer = KNNImputer(n_neighbors=5) df_imputed = imputer.fit_transform(df)
최적의 K값을 찾기 위해 GridSearchCV를 사용했는데, 실행시간이 오래걸렸고 구해진 K값으로 변경해도 유의미한 결과가 나오지 않았다.
최종적으로 사용할 모델이 정해진 후에 성능 향상을 위해 진행해야 할 부분을 너무 앞서 진행한 것이 아닌가 하는 생각이 든다.
from sklearn.model_selection import GridSearchCV # KNN 모델과 탐색할 K 값 범위 설정 knn = KNNImputer() param_grid = {'n_neighbors': [1, 3, 5, 7, 9]} # 원하는 K 값 범위 설정 # GridSearchCV를 사용하여 최적의 K 값을 찾음 grid_search_condition = GridSearchCV(estimator=knn, param_grid=param_grid, scoring='neg_mean_squared_error', cv=5) grid_search_condition.fit(X_imputed_condition, y_condition) # 최적의 K 값 확인 best_k_condition = grid_search_condition.best_params_['n_neighbors'] print("Condition 모델에서 최적의 K 값:", best_k_condition) # Condition 모델에 최적의 K 값을 적용 imputer_condition = KNNImputer(n_neighbors=best_k_condition)
이렇게 결측치 제거를 완료한 후에, 윈도우 크기(16주)로 데이터를 분할하고 각 윈도우 내에서 스케일링 수행했다. 이와 같은 방식으로 0으로 표기되어있는 NaN 데이터의 영향을 최소화 시킨 채 데이터 스케일링을 완료했다. 이후 두 데이터셋은 합쳐 하나의 데이터셋으로 사용했다.
from sklearn.preprocessing import StandardScaler # 데이터 표준화 (Z-Score Normalization) scaler = StandardScaler() X_scaled = scaler.fit_transform(X) for i in range(0, len(time_series_data), window_size): window = time_series_data[i:i+window_size] # 스케일링을 위한 평균과 표준 편차 계산 mean = window.mean() std = window.std() # 윈도우 내 데이터 스케일링 scaled_window = (window - mean) / std scaled_data.extend(scaled_window)
-
이런 방식으로 데이터 전처리를 수행했는데, 0으로 채워진 값들이 특성마다 너무 많은 비율을 차지해서 전처리를 하면서도 이렇게 하는게 맞는 방법인지 계속 의문이 들었다.
✏️ 캐글에 참가해서 많이 시도해보자.
학습
시계열 데이터지만, 데이터의 양이 충분하지 않다고 생각되어 시계열 교차 검증을 지원하는 TimeSeriesSplit을 사용했다. 모델은 LSTM으로 train한 코드인데 결과는 처참했다..
import numpy as np
import pandas as pd
from sklearn.model_selection import TimeSeriesSplit
from tensorflow.keras.layers import LSTM
from sklearn.metrics import mean_squared_error, r2_score
# 시계열 교차 검증을 위한 TimeSeriesSplit 설정
n_splits = 5
tscv = TimeSeriesSplit(n_splits=n_splits)
# 결과 저장용 리스트
rmse_scores = []
r2_scores = []
# LSTM 모델 파라미터 설정
n_features = merged_df.shape[1]
n_steps = 16 * 7
# LSTM 모델 구축
model = Sequential()
model.add(LSTM(units=50, activation='relu', input_shape=(n_steps, n_features)))
model.add(Dense(1))
# 컴파일
model.compile(optimizer='adam', loss='mse')
# 교차 검증 및 모델 학습
for train_idx, val_idx in tscv.split(merged_df):
X_train, X_val = merged_df.iloc[train_idx], merged_df.iloc[val_idx]
y_train, y_val = merged_y.iloc[train_idx], merged_y.iloc[val_idx]
# 데이터 윈도우로 자르기
X_train = [X_train.iloc[i:i + n_steps].values for i in range(len(X_train) - n_steps + 1)]
y_train = [y_train.iloc[i + n_steps - 1].values for i in range(len(y_train) - n_steps + 1)]
X_val = [X_val.iloc[i:i + n_steps].values for i in range(len(X_val) - n_steps + 1)]
y_val = [y_val.iloc[i + n_steps - 1].values for i in range(len(y_val) - n_steps + 1)]
X_train = np.array(X_train)
y_train = np.array(y_train)
X_val = np.array(X_val)
y_val = np.array(y_val)
# 모델 학습
model.fit(X_train, y_train, epochs=20, verbose=0)
# 검증 데이터에 대한 예측
y_pred = model.predict(X_val)
# RMSE 계산
rmse = np.sqrt(mean_squared_error(y_val, y_pred))
rmse_scores.append(rmse)
print(f"Fold RMSE: {rmse}")
# R2 score 계산
r2 = r2_score(y_val, y_pred)
r2_scores.append(r2)
print(f"Fold R2_score: {r2}")
# 결과 출력
for i, (rmse, r2) in enumerate(zip(rmse_scores, r2_scores), start=1):
print(f"Fold {i}:")
print("RMSE:", rmse)
print("R2_score:", r2)
print()
# RMSE와 R2 점수의 평균 계산
avg_rmse = np.mean(rmse_scores)
avg_r2 = np.mean(r2_scores)
# 평균값 출력
print("RMSE:", avg_rmse)
print("R2_score:", avg_r2)
- RMSE: 288560.59766739194
- R2_score: -1.4706110330156714
r2값이 0.4라면 40%의 설명력을 가진다고 해석하면 된다. 분야와 연구자에 따라 결정계수의 수치가 어디부터 실질적으로 적용 가능한지는 다르지만 일반적으로 20%는 넘어야 한다.
만약 r2값이 음수라면 데이터가 arbitrarily한 경우이거나, 독립 변수의 일괄 평균으로 예측하는 것보다 성능이 떨어진다는 것을 의미한다.
https://aliencoder.tistory.com/34
RNN으로도 유사한 결과가 나왔다. 데이터 가공방식의 변경이나 모델 튜닝을 진행할지, 접근 방식을 변경할지 고민하던 와중에 팀원이 트리 기반의 앙상블 모델이 훨씬 좋은 성능을 보인다는 것을 발견했다. 따라서 시계열 기반 예측 모델을 사용하지 않기로 했다.
