Paper : https://arxiv.org/abs/2306.16788
Github : https://github.com/ZIB-IOL/SMS

Abstract

---

신경망은 가지치기를 통해 상당히 압축될 수 있으며, 저장 및 계산 요구를 줄이면서도 예측 성능을 유지할 수 있다. Model Soups는 여러 모델의 파라미터를 단일 모델로 평균화하여 일반화 및 분포 외(OOD) 성능을 향상시키며, 추론 시간은 증가하지 않는다. 하지만 임의의 희소 모델을 평균화하면 서로 다른 희소 연결성 때문에 전체 희소성이 감소하기 때문에 희소성과 파라미터 평균화를 동시에 달성하는 것은 어렵다.

이 연구는 배치 순서나 가중치 감소와 같은 다양한 하이퍼파라미터 설정으로 단일 Iterative Magnitude Pruning 재훈련 단계를 탐색하여 평균화에 적합한 모델을 생성하고, 이러한 모델이 설계상 동일한 희소 연결성을 공유한다는 것을 보여준다. 이러한 모델을 평균화하면 개별 모델보다 일반화 및 OOD 성능이 크게 향상된다.

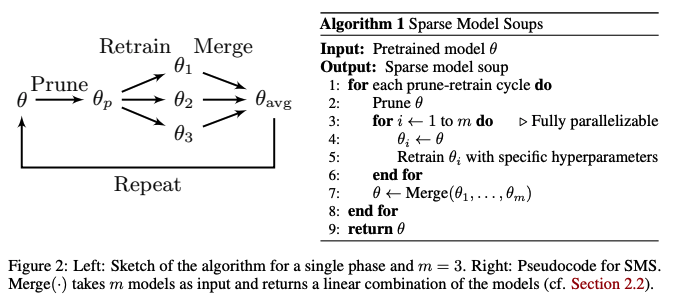
이를 바탕으로 SPARSE MODEL SOUPS(SMS)를 소개한다. SMS는 각 가지치기-재훈련 사이클을 이전 단계의 평균화된 모델로 시작하여 희소 모델을 병합하는 새로운 방법이다. SMS는 희소성을 유지하고, 희소 네트워크의 이점을 활용하며, 모듈화 및 완전 병렬화가 가능하며 IMP의 성능을 크게 향상시킨다. 또한 SMS는 최첨단 가지치기-훈련 중 접근 방식을 향상시키기 위해 적응될 수 있음을 보여준다.

1. Introduction

---

최첨단 신경망 아키텍처는 일반적으로 수백만 또는 수십억 개의 파라미터를 사용하는 과도한 매개변수 설정에 의존한다. 그 결과, 이러한 모델은 상당한 메모리 요구 사항을 가지며 훈련 및 추론 과정에서 계산 요구가 높다.

그러나 최근 연구는 Pruning, 즉 개별 파라미터나 그룹을 제거하여 이러한 자원 요구를 크게 줄일 수 있음을 보여주었다. 결과적으로 생성된 희소 모델은 저장 및 추론 중 부동 소수점 연산(FLOPs) 요구가 훨씬 적으면서도 밀집 모델과 유사한 성능을 유지한다.

다른 연구 분야에서는 여러 모델을 활용하여 예측기의 성능을 크게 향상시킬 수 있음을 보여주었다. 보류된 검증 데이터셋에서 가장 좋은 모델을 선택하고 나머지를 버리는 대신, 이러한 앙상블은 개별적으로 훈련된 여러 모델의 출력 예측을 평균화한다.

예측 앙상블은 예측 성능을 향상시키고, 보정, 분포 외 일반화, 모델 공정성 등 예측 불확실성 메트릭에 긍정적인 영향을 미치는 것으로 나타났다.

앙상블의 중요한 단점은 배포 중 모든 모델을 평가해야 한다는 점으로, 추론 비용이 m배로 증가한다는 것이다. 이 문제는 일부 희소화된, 더 효율적인 모델 앙상블을 활용하여 부분적으로 해결되었다.

여러 연구는 대신 파라미터를 평균화하여 추론을 위한 단일 모델을 구성할 것을 제안한다. 예측 앙상블과 달리, 이러한 모델 수프는 모델이 손실 풍경의 선형적으로 연결된 분지에 위치해야 한다. 그러나 서로 다른 랜덤 시드로 동일한 초기화로 모델을 처음부터 훈련하면 개별 모델보다 성능이 훨씬 떨어지는 파라미터 평균을 생성하는 경우가 많다.

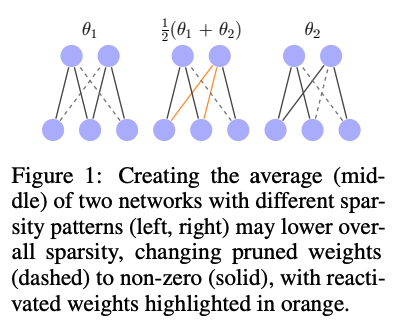
최근 연구는 단일 분지 내에서 정렬하기 위해 뉴런 순열을 조사하고 있다. 평균화에 적합한 네트워크를 식별하는 초기 과제 외에도 희소 네트워크의 계산적 이점을 활용하려 할 때 또 다른 문제가 발생한다. 서로 다른 희소 연결성을 가진 모델을 평균화하면 전체 희소성이 감소하고, 다시 가지치기가 필요할 수 있으며, 이는 성능 저하를 초래할 수 있다.

이 연구에서는 희소성을 활용하면서 여러 모델을 단일 모델로 결합하는 이점을 동시에 활용하는 문제에 도전한다.

전이 학습 분야의 최근 연구에서 영감을 받았다. pretrained model의 여러 복사본을 랜덤 시드만 다르게 하여 미세 조정하면, 평균화에 충분히 유사하고 일반화 개선을 위해 충분히 다양한 모델을 생성할 수 있음을 보여주었다.

본 논문의 핵심은 표준 학습 후 가지치기 전략, 예를 들어 IMP의 단일 prune-retrain 단계가 전이 학습 패러다임과 밀접하게 유사하다는 관찰에 있다. Pretrained model에서 시작하여, 최적화 목표는 가지치기에 의해 부과된 새로운 대상 도메인 또는 하위 공간 제약으로 인해 갑작스럽게 변하며, 이어서 pruning 후 회복을 위해 'retraining'과 상호 교환적으로 사용되는 'fine-tuning'이라는 훈련 과정이 따른다.

전이 학습의 fine-tuning 단계와 마찬가지로 pruning 후 retraining 단계에서 다양한 하이퍼파라미터 설정을 탐색하면 설계상 동일한 희소 연결성을 공유하면서 평균화에 적합한 모델을 생성할 수 있음을 발견했다.

이러한 희소 평균은 개별 모델과 m배 재훈련된 모델보다 우수한 성능을 보이며, 효과적으로 IMP의 실행 시간을 줄인다. 또한, 본 논문에서는 방금 얻은 평균화된 모델에서 다음 pruning-retraining 사이클을 시작하여, 개별 재훈련 실행의 성능도 향상시킨다.

본 논문에서 제안하는 Sparse Model Soups는 앞서 언급한 문제를 해결하고, m에 독립적인 추론 복잡성을 가능하게 하며, pretrained model을 활용하여 처음부터 훈련할 필요 없이 희소성 패턴을 유지하면서 희소성 이점을 활용하며, IMP의 일반화 및 OOD 성능을 크게 향상시킨다.

Contributions

1. 잘 훈련된 모델을 가지치기하고 배치 순서, 가중치 감소, 재훈련 기간 및 길이 등 다양한 하이퍼파라미터로 여러 복사본을 재훈련하면, 개별 구성 요소보다 우수한 일반화 및 OOD 성능을 보이는 평균화된 모델을 생성할 수 있음을 증명한다. 중요한 점은 이러한 모델들이 pruning된 부모 모델의 희소성 패턴을 유지하면서 파라미터 평균에서 보존된다는 것이다.

2. IMP의 각 prune-retrain 단계를 평균화된 모델에서 시작하는 아이디어를 활용하여 희소 모델을 단일 분류기로 병합하는 새로운 방법인 Sparse Model Soups(SMS)를 제안한다. SMS는 두 가지 방법으로 IMP의 성능을 크게 향상시킨다:

   • 평균화는 일반화 및 OOD 성능 측면에서 개별 모델을 능가한다.

   • 평균화된 모델에서 재훈련된 모델은 단일 모델에서 재훈련된 모델보다 더 나은 성능을 보인다.

3. 본 논문의 발견을 훈련 중 pruning 영역으로 확장하여, SMS의 다재다능성을 입증하며 이를 여러 다른 최첨단 접근 방식과 통합한다. 이는 성능을 크게 향상시키고, 훈련 중 희소화를 수행하는 다른 주요 방법들과의 경쟁력을 높인다.

2. Methodology: Sparse Model Soups

2.1 Preliminaries

---

앞서 소개한 IMP 접근 방식과 같이 개별 가중치를 제거하는 모델 가지치기에 중점을 둔다. IMP는 학습 후 가지치기 알고리즘으로, 세 단계 파이프라인을 따른다.

• Pretrained model을 시작으로
• 특정 임계값 이하의 가중치를 pruning하고
• retraining을 통해 예측 성능을 복원한다.

이 prune-retrain 사이클은 여러 번 반복되며, 각 pruning 단계의 임계값은 미리 정의된 단계 수 후 목표 희소성을 달성하기 위해 적절한 백분위수로 결정된다. 최근 연구는 magnitude pruning이 더 복잡한 알고리즘과 경쟁할 만한 성능을 가진 희소 모델을 생성함을 보여주었다.

m개의 희소 모델 f_θi가 가중치 θ_i ∈ R^n, i∈{1,...,m}를 가지는 경우, 예측 앙상블은 모델의 출력을 평균한 것과 동등한 기능을 하는 모델을 구성한다. 이 앙상블은 평가를 위해 m번의 순방향 패스가 필요하지만, 전체 희소성 수준을 유지한다.

반면, 본 논문은 다른 모델의 선형 결합인 단일 모델의 성능과 희소성에 중점을 둔다. 스칼라 λ_i ∈ R가 주어지면, 가중치가 주어진 예측 함수 f_thetā를 고려한다:

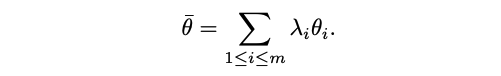
모든 i에 대해 λ_i =1/m인 경우, thetā는 모든 네트워크의 평균을 나타낸다.

임의의 희소 모델의 가중치를 평균화하면 전체 희소성이 감소할 수 있다. 이는 다른 네트워크가 서로 다른 희소 연결성을 가질 수 있어 평균화 과정에서 텐서의 0을 제거하기 때문이다.

이 문제를 해결하기 위해 thetā를 원래 네트워크의 희소성 수준에 맞추기 위해 다시 pruning한다. 그러나 이러한 접근 방식은 희소성 패턴이 크게 다를 경우 pruning 유발 성능 저하가 발생할 수 있다는 단점이 있다.

2.2 SPARSE MODEL SOUPS

---

전이 학습 분야의 최근 발전에서 영감을 받아, pretrained model에서 fine-tuning된 모델이 동일한 손실 분지에 위치할 수 있으며, 이를 결합하여 soup를 만들 수 있음을 보여준다. 본 논문은 동일한 pruning된 모델에서 재훈련하는 동안 유사한 행동을 달성할 수 있다고 가정한다.

본 논문의 동기는 전이 학습 패러다임과 IMP의 단일 단계 사이의 유사성에서 비롯된다. 소스 도메인에서 대상 도메인으로 전환할 때 최적화 목표가 갑작스럽게 변경되며, 새로운 목표를 최소화하기 위해 적응(즉, fine-tuning)이 필요하다. 유사하게, '강한' 가지치기는 손실을 갑작스럽게 변경하고, 새로 추가된 희소성 제약을 고려하여 적응(즉, retraining)이 필요하다.

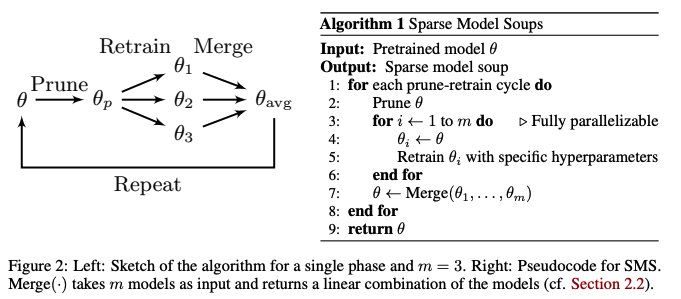
이 아이디어의 단일 단계는 그림 2의 왼쪽에 설명되어 있다.

• Pretrained model의 가중치 θ가 pruning되어 모델 θp 를 생성하고, 이를 m번 복제한다. 이 설정에서 pruning된 가중치는 영구적으로 훈련 불가능한 상태로 남는다.

• 이후, m개의 모델 각각은 다양한 하이퍼파라미터 설정(예: 랜덤 시드, 가중치 감소 요인, 재훈련 길이, 학습률 스케줄)을 사용하여 독립적으로 재훈련된다.

• 마지막으로, m개의 재훈련된 모델이 단일 모델로 병합된다.

이 과정은 모든 m개의 재훈련된 모델 θ1 ,...,θm 이 고정된 pruning 마스크를 가진 동일한 희소성 패턴을 공유하도록 보장한다. 그러나 여러 가지치기-재훈련 사이클 후 모델을 결합할 때 모든 모델 간 동일한 희소 연결성이 보장되지 않는다.

이를 해결하기 위해 각 단계 후 모델을 평균화하고, 이전에 평균화된 모델로 다음 단계를 시작한다. 이로 인해 SMS라는 방법이 도출되며, 그림 2의 오른쪽에 의사 코드로 제시된다.

SMS는 여러 이점을 제공하며 주요 과제를 해결한다.

1. 최종 모델의 추론 복잡성은 m에 독립적이다. 이 방법은 모듈화가 높아, 각 단계에서 다양한 하이퍼파라미터 설정과 서로 다른 m을 허용한다.

2. m 모델의 재훈련은 완전히 병렬화되어 효율성이 향상된다(3.2절 참조).

3. 각 단계를 이전 단계에서 병합된 모델로 시작함으로써 희소성 패턴이 유지되고, 희소 네트워크의 이점을 활용할 수 있다. 사이클 수가 증가함에 따라 네트워크가 더 희소해져 추가적인 효율성 향상이 가능해진다.

4. SMS는 처음부터 훈련할 필요 없이 대규모 pretrained model의 이점을 효과적으로 활용한다.

모델을 효과적으로 병합하여 일반화를 향상시키는 것은 도전적일 수 있다. 모델들이 멀리 떨어질 수 있기 때문이다. 본 논문에서는 주로 Wortsman et al. (2022a)에서 제안된 두 가지 볼록 조합 방법인 UniformSoup과 GreedySoup을 사용한다.

UniformSoup은 각 모델을 동일하게 가중치(λi = 1/m)한다. 반면, GreedySoup은 검증 정확도에 따라 모델을 정렬하고, 이전 하위 집합에 대한 검증 정확도를 개선하는 경우에만 모델을 순차적으로 포함한다.

4. Related Work

---

희소성과 관련된 연구 문헌을 검토한다. 희소화 접근법에 대한 포괄적인 리뷰는 Hoefler et al. (2021)을 참조.

모델 평균화

Stochastic Weight Averaging (Izmailov et al., 2018)은 SGD 경로를 따라 파라미터를 평균화하여 일반화를 향상시킨다.

Wortsman et al. (2022a)와 Rame et al. (2022)은 다양한 하이퍼파라미터로 미세 조정된 모델을 평균화하여 모델 수프의 일반화 및 OOD 성능이 향상된다고 보여준다.

섹션 3.3에서 본 논문의 접근 방식과 가장 유사한 것은 Late-phase learning (von Oswald et al., 2020)으로, 특정 파라미터를 독립적으로 훈련하고 평균화하지만 가지치기는 하지 않는다.

Gueta et al. (2023)은 언어 모델의 미세 조정을 탐구하며, 서로 가까운 모델 주위의 영역에 잠재적으로 우수한 모델이 포함될 수 있음을 밝혀냈다.

Croce et al. (2023)은 적대적 강건 모델의 수프를 탐구하고, Choshen et al. (2022)은 여러 미세 조정된 모델을 병합하여 기본 모델을 향상시킨다.

Wortsman et al. (2022b)은 제로샷과 미세 조정된 모델을 평균화하여 강건한 미세 조정을 도입한다.

SMS와 유사하게, Jolicoeur-Martineau et al. (2023)은 독립적으로 훈련된 모델을 정기적으로 평균화하지만 가지치기는 하지 않는다.

희소성과 파라미터 평균화를 결합하는 기존 연구와 본 논문의 작업 사이의 주요 차이점을 강조한다.

Yin et al. (2022b)는 dynamic sparse training을 사용하여 고정된 하이퍼파라미터로 단일 실행 내에서 모델을 평균화하는 반면, 본 논문의 방법은 다양한 하이퍼파라미터 설정을 가진 여러 실행에서 모델을 평균화하는 prune-after-training 방법이다.

그들의 prune-and-grow 접근법은 다양한 희소성 패턴을 탐구하고 희소성을 유지하기 위해 다시 pruning를 요구하는 반면, 본 논문의 방법은 일관된 희소성 패턴을 유지하여 다시 pruning을 의도적으로 피한다. 이 접근 방식이 re-pruning 접근 방식(IMP-RePrune)을 크게 개선함을 명확히 보여준다. 이는 재가지치기의 영향을 완화하기 위해 설계된 CIA나 CAA 같은 전략을 사용할 때도 마찬가지다.

마찬가지로, Yin et al. (2022a)는 weight rewinding을 사용한 IMP를 사용하여 단일 훈련 경로에서 다양한 prune-retrain 사이클의 IMP 서브 네트워크를 평균화하지만, 이 접근법도 re-pruning을 필요로 한다. 반면, 본 논문의 접근 방식은 병렬로 훈련된 모델을 평균화하는 것이다. 또한, 그들의 목표는 희소한 모델을 생성하는 것이 아니라 복권 티켓을 생성하는 것이다.

유사하게, Stripelis et al. (2022)는 다수결 투표를 통해 지역 클라이언트 마스크로 글로벌 마스크를 중앙 업데이트하는 Federated Learning 알고리즘인 FedSparsify를 소개한다.

또한, 본 논문의 작업은 Jaiswal et al. (2023)의 연구와도 다르다. 그들은 마스크 생성을 위한 초기 가지치기 마스크를 평균화하는 데 중점을 두는 반면, SMS는 희소 모델의 파라미터를 평균화하는 데 중점을 둔다.

모드 연결성

Neyshabur et al. (2020)는 처음부터 훈련된 모델들이 선형적으로 연결되지 않는 반면, 사전 훈련된 모델을 미세 조정한 모델들은 유사하며 동일한 손실 베이슨 내에 위치한다고 보여준다.

Entezari et al. (2022)는 다른 시드로 훈련된 모델들이 뉴런 순열에 대해 선형적으로 연결된다고 추측한다.

Ainsworth et al. (2023)은 모델을 공유된 손실 베이슨으로 변환하기 위한 순열 알고리즘을 제안하며, Singh & Jaggi (2020)는 뉴런 소프트 정렬을 위한 모델 퓨전을 적용해 밀집 모델을 희소 모델로 통합하면서 필터 pruning을 향상시킨다.

마찬가지로, Benzing et al. (2022)는 초기화 시점에서도 모델이 손실 계곡을 공유함을 보여주는 순열 알고리즘을 도입한다.

Jordan et al. (2022)는 딥 네트워크의 보간에서 '분산 붕괴'를 탐구하고 이를 완화하기 위한 전략을 제안한다.

여러 연구(Frankle et al., 2020; Evci et al., 2022; Paul et al., 2023)는 가중치 리와인딩(IMP-WR)과 함께 IMP의 무작위성에 대한 안정성을 연구한다.

Evci et al. (2022)는 훈련된 복권 티켓과 IMP-WR 솔루션이 동일한 분지로 수렴함을 보여주고, Paul et al. (2023)은 다양한 희소성에서 연속적인 IMP-WR 솔루션이 선형 모드로 연결되어 손실 안정성을 유지함을 발견한다.

예측 앙상블

여러 연구는 여러 모델의 출력을 평균화하는 예측 앙상블에 초점을 맞춘다(Lakshminarayanan et al., 2017; Huang et al., 2017; Garipov et al., 2018; Mehrtash et al., 2020; Chandak et al., 2023).

희소성 맥락에서 Liu et al. (2021)은 다양한 앙상블 후보의 효율적 생성을 위해 DST를 활용한다.

Whitaker & Whitley (2022)는 모델 복사본을 무작위로 pruning하고 retraining하여 앙상블을 구성하고, Kobayashi et al. (2022)는 사전 훈련된 모델의 하위 네트워크를 미세 조정한다.

앙상블에 대한 설문 조사는 Ganaie et al. (2021)을 참조.

5. Discussion

---

효율적이고 성능이 높은 희소 네트워크는 자원이 제한된 환경에서 매우 중요하다. 하지만 희소 모델은 파라미터 평균화의 이점을 쉽게 활용할 수 없다.

이 문제를 해결하기 위해 SMS라는 기술을 제안했다. 이 기술은 희소성을 유지하면서 모델을 병합하여 IMP를 크게 향상시키고 여러 기준을 능가한다.

SMS를 훈련 중의 크기 기반 가지치기 방법에 통합함으로써 성능과 경쟁력을 높였다.

비록 Pruning, 즉 네트워크 압축의 한 종류에 초점을 맞췄지만, 본 논문의 연구는 희소화 알고리즘을 이해하고 개선하는 중요한 단계로 작용할 것이라고 생각한다.

Average Models Code

---

def average_models(self, soup_list: list[Candidate], soup_weights: torch.Tensor = None,
                   device: torch.device = torch.device('cpu')):
    if soup_weights is None:
        soup_weights = torch.ones(len(soup_list)) / len(soup_list)
    ensemble_state_dict = OrderedDict()

• soup_list: 앙상블에 포함될 모델들의 리스트

• soup_weights: 각 모델에 할당된 가중치

• ensemble_state_dict: 앙상블 모델의 파라미터를 저장할 OrderedDict

for idx, candidate in enumerate(soup_list):
    candidate_id, candidate_file = candidate.id, candidate.file
    state_dict = torch.load(candidate_file, map_location=device)
    for key, val in state_dict.items():
        factor = soup_weights[idx].item()  # No need to use tensor here
        if '_mask' in key:
            # We dont want to average the masks, hence we skip them and add later
            continue
        if key not in ensemble_state_dict:
            ensemble_state_dict[key] = factor * val.detach().clone()  # Important: clone otherwise we modify the tensors
        else:
            ensemble_state_dict[key] += factor * val.detach().clone()  # Important: clone otherwise we modify the tensors

• 각 후보 모델에 대해, 모델 파일을 로드하고 state_dict로 파라미터를 가져온다.

• factor : 해당 모델의 가중치

• _mask로 끝나는 키 : 마스크 파라미터를 의미하며, 이들은 평균하지 않고 나중에 추가된다.

• ensemble_state_dict에 각 파라미터의 가중치를 적용하여 합산한다. 처음 등장하는 파라미터는 초기화하고, 이후 등장하는 동일한 파라미터는 합산한다.

# Add the masks from the last state_dict
for key, val in state_dict.items():
    if '_mask' in key:
        ensemble_state_dict[key] = val.detach().clone()

return ensemble_state_dict

• 마지막 모델의 마스크 파라미터를 ensemble_state_dict에 추가한다. 이는 마스크 파라미터가 가중치 평균에 포함되지 않도록 하기 위함이다.

• 최종적으로 완성된 ensemble_state_dict를 반환한다.