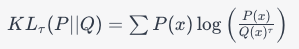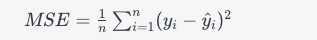[UROP #6] Understanding and Improving Knowledge Distillation for Quantization Aware Training of Large Transformer Encoders

Github : https://github.com/MarsJacobs/kd-qat-large-enc

Paper : https://aclanthology.org/2022.emnlp-main.450/

💡 로 표시된 부분은 제가 이해한 내용을 적은 부분입니다. 오류가 있다면 댓글로 남겨주세요 🙏🏻

---

Abstract

어떤 KD 접근 방식이 Transformers의 Quantization Aware Training에 가장 적합한지에 대해 알려진 것이 매우 적다. 이 연구에서는 양자화된 대형 Transformers의 어텐션 회복 메커니즘에 대한 분석을 제공한다.

특히, 이전에 채택된 "어텐션 스코어에 대한 MSE 손실"이 self-attention information을 회복하는 데 충분하지 않다는 것을 밝혀냈다.

따라서 두 가지 KD 방법을 제안한다 :

• attention-map 손실
• attention-output 손실
  
  

더 나아가 어텐션 맵과 출력 손실 간의 작업 의존적 선호도를 다루기 위해 두 손실을 통합한다.

다양한 Transformer 인코더 모델에 대한 실험 결과는 제안된 KD 방법이 하위 2비트 가중치 양자화를 사용한 QAT의 최신 정확도를 달성한다는 것을 보여준다.

---

Introduction

많은 경우, Kullback-Leibler Divergence은 선생님과 학생의 soft 레이블을 맞추기 위한 기본 증류 목표로 사용된다.

Kullback-Leibler Divergence (KL-Div)

두 확률 분포 간의 차이를 측정하는 데 사용된다. (자세한건 사이트 를 참고)

그러나 KD에 대한 추가적인 연구는 내부 표현이 선생님의 중간 지식을 전달한다는 것을 제안하며, 선생님과 학생 간의 레이어의 hidden state knowledge의 거리(평균 제곱 오차, MSE)를 최소화하는 것도 제안되었다.

KD는 대규모 Transformer 기반 언어 모델을 효율적으로 배치하기 위한 필수적인 모델 압축 기술이다. 인기 있는 Transformer 인코더 모델인 BERT는 수억 개의 매개변수를 포함하며 깊은 메모리 및 계산 부하를 유발하므로, 이러한 대규모 모델은 모델 풋프린트를 10에서 100배까지 줄이기 위해 극단적인 압축이 필요하다.

따라서 더 적은 매개변수를 달성하기 위한 다양한 학생 모델의 압축에 중점이 두어 왔지만, 그 초점은 제한적으로 적은 매개 변수를 달성하는 것에 국한된다.

Hard Label

: 레이블을 일반적인 레이블 형태로 표현하는 것을 의미한다.

• 클래스 중 하나의 정수 값으로 나타내며 해당 예제가 정확히 어떤 클래스에 속하는지를 명시한다.
  

Soft Label

: 레이블을 확률 분포 또는 연속적인 값으로 표현하는 것을 의미한다.

• 예제가 각 클래스에 속할 확률을 나타내는 확률값으로 표시된다.
• 다중 클래스 분류의 경우, 각 클래스에 대한 확률값을 포함하는 벡터로 볼 수 있다.

Quantization-aware training (QAT)은 최근에 Transformer 모델의 메모리 요구 사항 및 계산 복잡성을 줄이는 데 성공한 기법으로 주목받고 있다.

그러나 대규모 Transformer 모델과 관련하여 어떤 KD 접근 방식이 QAT에 가장 적합한지에 대한 이해가 부족하다.

실제로 이전 연구에서는 주로 모델 출력에 대한 기본적인 KL-Div 손실 외에도 어텐션 스코어와 Transformer 출력의 레이어별 지식 증류를 채택하였지만 이러한 KD 설정이 BERT-Large와 같은 대규모 Transformer 인코더에 대한 QAT에 가장 도움이 되는지에 대한 근거가 없다.

BERT-Base의 경우, KL-Div 기반의 어텐션 맵에 기반한 KD 기술이 어텐션 스코어의 MSE 손실을 사용하는 이전 KD 기술을 능가한다는 것을 발견했다.

그러나 양자화된 가중치가 많은 레이어가 있는 경우 특정 NLP 작업에 대한 어텐션 전파를 방해하므로 어텐션 맵 손실은 대규모 Transformer 인코더에는 충분하지 않다.

따라서 어텐션 출력에 대한 MSE 손실을 개발하여 다수의 레이어를 통해 어텐션 회복을 돕는 데 도움을 준다.

• 대규모 Transformer 인코더의 정확도를 향상시키기 위해 QAT에 대한 이전 KD 기술을 개선했다.

• 어텐션 맵 손실 (KL-Div 기반)이 기존의 어텐션 스코어 손실 (MSE 기반)을 능가한다는 것을 양적으로 보여준다. 특히 BERT-Base 모델에 특히 유용하다.

• BERT-Large에서 뚜렷하게 나타나는 작업에 종속적인 어텐션 특성을 발견했다. 특히 양자화된 가중치로 인해 큰 Transformer에서 어텐션 출력의 동질화가 발생한다. 이 문제를 해결하기 위해 새로운 KD 방법인 어텐션 출력 손실을 제안한다.

• 어텐션 맵 및 출력 손실을 통합하여 작업에 종속적인 어텐션 특성을 포괄적으로 처리하는 가능성을 탐구했다.

• 다양한 대규모 Transformer 인코더 및 NLP 작업에서 제안된 KD 방법을 평가하며, 하위 2비트 양자화에 대한 QAT의 최신 정확도를 달성했다.

---

Prior KD Techniques for QAT

QAT에 일반적으로 사용되는 KD 기술은 아래 두가지가 포함된다.

1) 전체 레이어 증류
2) SA-GEN에 대한 증류

All-Layer Distillation for QAT

일반적으로 교사의 내부 표현, 즉 레이어 출력과 같은 것은 모델 압축을 위한 지식 증류에 널리 사용된다. 그러나 전형적인 모델 압축과 양자화 간에 KD에서는 명확한 차이가 있다.

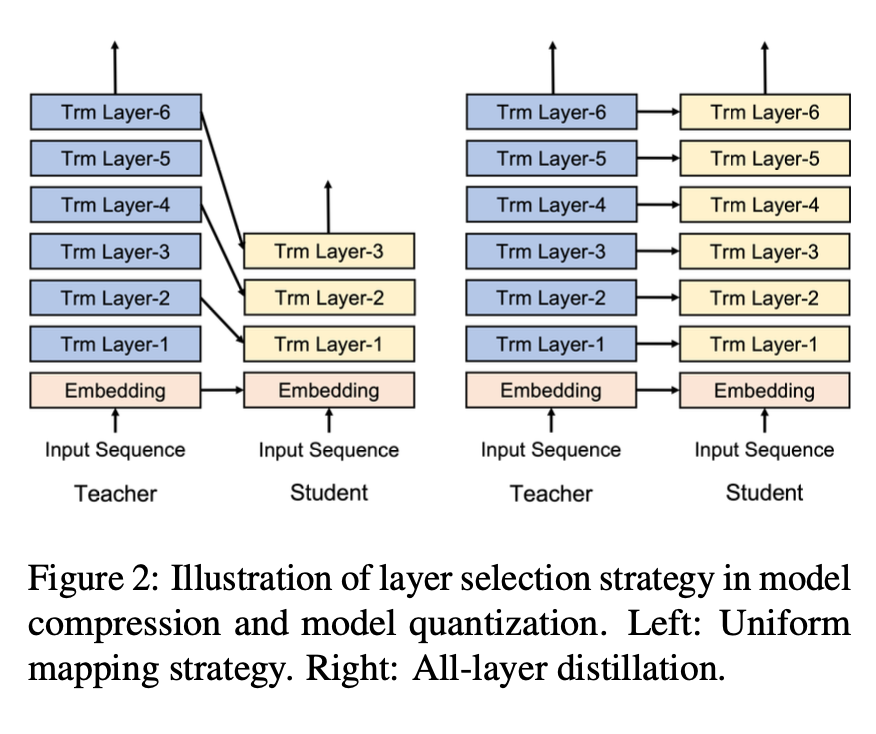
KD의 대표적인 레이어 간 매핑 두 가지를 보여준다. 모델 압축을 위한 선택된 레이어 증류 (왼쪽) 및 QAT를 위한 전체 레이어 증류 (오른쪽).

선택된 레이어 증류의 경우, 연구는 hidden state knowledge (HSK)을 더 많이 증류함에 따라 HSK의 한계적인 효용이 감소한다는 것을 보여주었다.

반면, 대부분의 이전 QAT 방법은 모든 레이어의 Transformer 출력에 KD를 적용했다. QAT 방법의 교사와 학생의 구조적 동등성은 이 선택을 자연스럽게 만들었지만, 그에 대한 정당성은 거의 없다.

따라서, 가중치 매개변수에 적용되는 양자화가 Transformer 레이어의 기능을 방해하며 레이어별 지도가 필요하다고 가설을 세웠다.

BERT-Base에서 선택된 레이어 증류와 전체 레이어 증류 간의 스펙트럼 비교

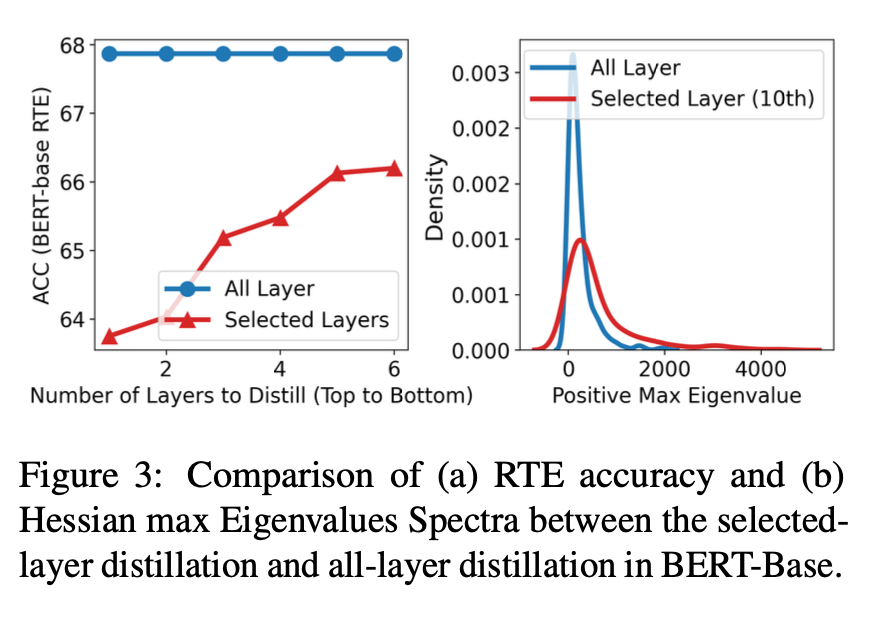
(a) RTE 정확도

(b) Hessian max Eigenvalues

1. 선택된 레이어 증류에서 증류된 레이어 수가 다른 경우의 정확도를 비교했다. (a)에서 볼 수 있듯이, RTE 정확도는 증류된 레이어 수와 함께 증가하며, 전체 레이어 증류가 선택된 레이어 증류보다 높은 성능을 보여준다.
   
   

2. (b)에서 Hessian max eigenvalues 관점에서 QAT 이후 선택적 레이어 증류 방식과 전체 레이어 증류 방식의 손실 표면을 비교했다.
   
   선택된 레이어 증류의 전략으로 단일 레이어 선택 증류를 채택했다. 특히, 단일 레이어 선택 증류로 성능이 가장 향상되었던 BERT-Base 모델의 10번째 레이어를 선택하는 방법을 사용했다.
   
   전체 레이어 증류는 Hessian 행렬의 고유값 대부분이 더 작은 크기를 가지는 것으로 보여 손실 표면이 더 "부드럽게" 변화함을 의미한다.
   
   따라서 layer-wise distillation이 양자화된 가중치 매개변수를 가진 학생 모델을 훈련하는 데 도움이 된다고 결론지을 수 있다.
   
   

Recognizing Textual Entailment (RTE)

주어진 두 문장 사이의 관계를 결정하는 작업이다. 보통 "entailment" (유추) 관계, "contradiction" (모순) 관계, "neutral" (중립) 관계 중 하나로 분류된다.

RTE 정확도는 이 작업에서 모델의 성능을 나타내는 지표로, 정확하게 올바른 관계를 예측한 경우의 비율이다. 예를 들어, 모델이 두 문장이 "entailment" 관계일 때 이를 정확하게 예측한 경우 RTE 정확도가 증가한다.

Hessian max eigenvalues

Hessian 행렬은 함수의 미분이 두 번째로 미분된 것을 나타내는 행렬로, 주어진 함수의 곡률 정보를 제공한다.

Hessian 행렬의 최대 고유값은 주어진 함수의 어떤 지점에서의 곡률이 얼마나 가팔라지는지를 나타내는 값이다.

최대 고유값이 큰 경우, 함수의 국부 최소값(local minimum) 또는 국부 최대값(local maximum) 주변에서 뾰족한 곡선이 형성되어 있음을 나타내며, 최소값 또는 최대값으로 수렴할 가능성이 높다.

최대 고유값이 작은 경우, 함수의 국부 최소값 또는 최대값 주변에서 곡선이 덜 가팔라지며, 수렴이 더 느릴 수 있다.

3.2 Improve KD on Self-Attention Generation

전체 레이어 지식 증류(KD)의 목표를 더 자세히 조사했다.

attention-score loss :

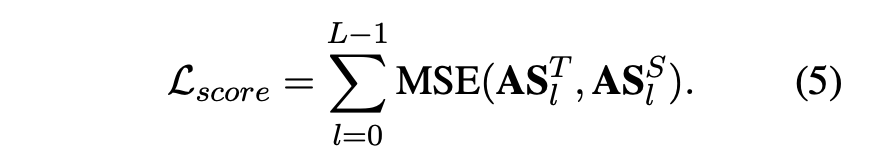
이전의 양자화-지식 증류(QAT) 방법은 전체 레이어 KD에 대해 주로 attention 스코어 대한 평균 제곱 오차(MSE) 손실을 사용했다.

그러나 attention 스코어 손실은 토큰 간의 상대적 중요성을 유지하기에 적합한 목표가 아니다.

💡 Attention Score는 디코더의 time step t에서 새로운 단어를 예측하기 위해, decoder의 hidden state st와 encoder의 hidden states h1~hN들이 얼마나 유사한지를 판단하는 점수이기 때문에, 토큰 간의 상대적 중요성을 유지하기에 적합하지 않다고 볼 수 있다.

attention-map loss:

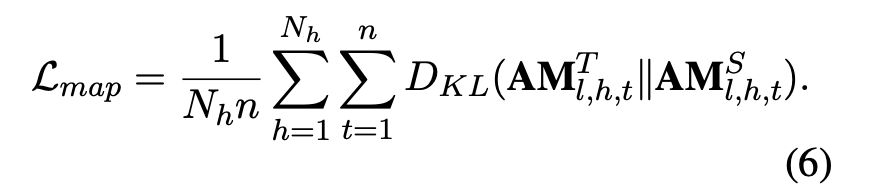
따라서, 본 연구에서는 KL-Div 손실을 사용한 attention 맵에 대한 손실을 제안했다.

이 손실은 토큰 간의 attention의 상대적 중요성을 더 잘 유지할 수 있도록 도와준다. attention-map loss는 이전에 모델 압축에 사용되었지만, QAT 맥락에서 attention-map loss의 이점을 최초로 양적으로 입증했다.

제안된 KD 손실을 양적으로 평가하기 위해 attention 맵을 특성화하는 두 가지 메트릭스를 소개했다.

• cover length ratio
  학생의 attention 맵이 교사의 attention 맵과 얼마나 다른지를 측정한다. 이를 위해 상위 K개의 토큰 커버리지를 기반으로 한다.

• ranking loss
  교사와 학생의 attention 순위 간의 유사성을 보여준다.

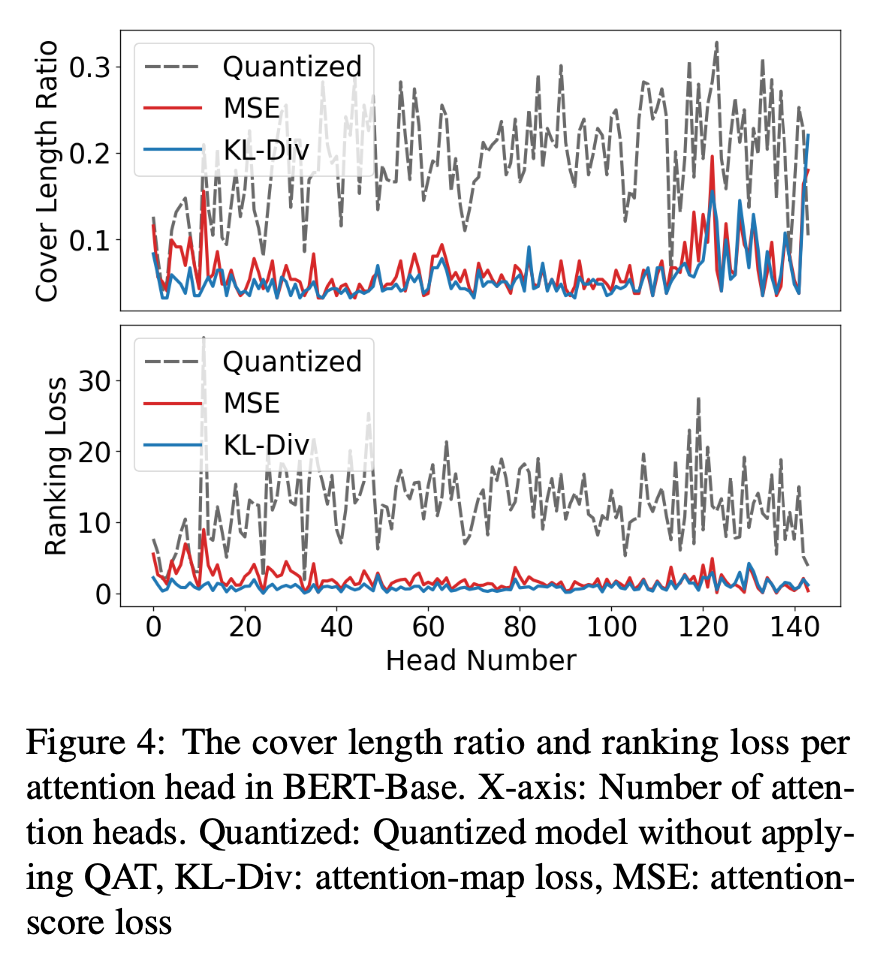
SST-2 작업에서 BERT-Base의 각 attention head의 cover length ratio와 ranking loss를 비교한다(다른 레이어와 작업에 대해서도 전반적인 경향은 동일하다).

Stanford Sentiment Treebank (SST-2)

자연어 처리 분야에서 사용되는 감정 분류 작업 중 하나로, SST-2 작업은 문장 또는 구문의 긍정적인 또는 부정적인 감정을 분류하는 작업이다.

그림에서 양자화는 cover length ratio와 ranking loss을 크게 증가시키며, attention의 상대적인 순위가 심각하게 왜곡되었다는 것을 나타낸다.

attention-score loss는 이러한 왜곡을 줄이는 데 도움이 되지만 여전히 스파이크가 존재하는 반면, attention-map loss는 스파이크를 성공적으로 억제하고 attention 맵의 상대적 중요성을 유지한다.

또한, KD의 목표가 QAT 정확도에 미치는 영향을 더 잘 이해하기 위해 KL-Div의 온도 변화 실험을 수행했다.

KL-Div 손실의 그래디언트는 온도가 충분히 큰 경우 MSE 손실의 그래디언트로 단순화될 수 있기 때문에 온도 값을 (τ) 스윕하여 KL-Div 손실의 행동을 관리할 수 있다.

KL-Divergence (KL-Div) 손실: KL-Div 손실은 두 확률 분포 간의 차이를 측정하는 데 사용된다.

MSE (Mean Squared Error) 손실: MSE 손실은 예측 값과 실제 값 사이의 제곱 오차를 측정하는데 사용된다.

💡 τ = 1

• KL-Div 손실에서 t = 1일때, 기존의 KL-Div 손실과 동일하다. KL-Div는 두 분포의 차이를 강조하며, 각 분포의 개별 특성을 중요시한다.
• attention-map 손실을 이용하여 각 레이어에서 중요시 하는 부분 대한 정보를 전달하는 데 두 분포간의 차이를 고려해야하므로, attention-map 손실과 유사하다고 할 수 있다.

💡 τ = inf

• KL-Div 손실에서 t = inf이면, KL-Div 손실은 두 분포의 차이를 거의 고려하지 않고, 결과값에 집중하게 된다.
• attention-score란 현재 디코더의 시점 t에서 단어를 예측하기 위해, 인코더의 모든 은닉 상태 각각이 디코더의 현 시점의 은닉 상태 st와 얼마나 유사한지를 판단하는 스코어값이다.
  출처 : https://wikidocs.net/22893
• attention-map 손실처럼 두 분포의 차이에 집중하는 것이 아니라 MSE처럼 전체를 고려해서 최종적인 값에 대한 손실을 고려하므로, attention-score 손실과 유사하다고 볼 수 있다.

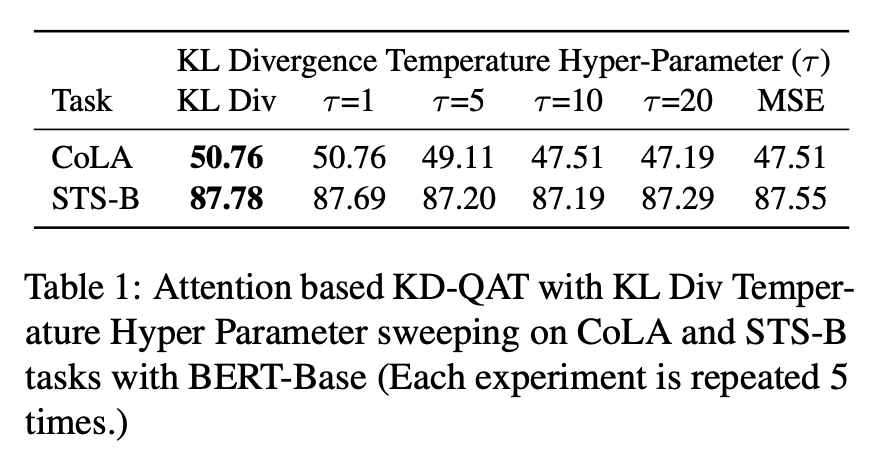
표 1은 다양한 τ에 대한 CoLA 및 STS-B에서의 BERT-Base의 QAT 정확도를 보여준다.

표에서 볼 수 있듯이, 손실 항이 attention-map loss와 유사해질수록 양자화된 모델의 정확도가 증가한다. 이러한 성능 향상에서 다음과 같은 정보를 알 수 있다.

1) 레이블 매칭은 SA-GEN에서의 QAT를 보상하는 데 중요하다.
2) attention-map loss는 레이블 매칭에 더 효과적이다.

즉, attention-map loss가 학습 중에 레이블 매칭을 더 잘 지원하여 양자화된 모델의 정확도를 높이는 데 도움이 되는 것으로 나타났다.

---

KD for QAT on Large Transformers

1. task-dependent 특성으로 인한 attention-map 손실의 한계를 밝힌다.

2. 도전 과제를 해결하기 위해 새로운 KD 손실인 attention-output loss를 제안한다.

3. 두 가지 손실의 결합을 제안하여 task-dependent 특성을 다루는 방법을 제시한다.

Task-Dependent Characteristics

하위 미세 조정에 동일한 사전 훈련된 모델을 사용하지만 task에 따라 attention의 특성이 다양하게 변한다.

residual connections 즉, SA-PROP 활성화의 이상치가 특정 attention 패턴을 형성한다는 연구 결과가 있었다.

따라서, 양자화에 대한 task-dependent 특성을 이해하기 위해 attention 출력의 min-max 곡선을 통해 이상치를 조사했다.

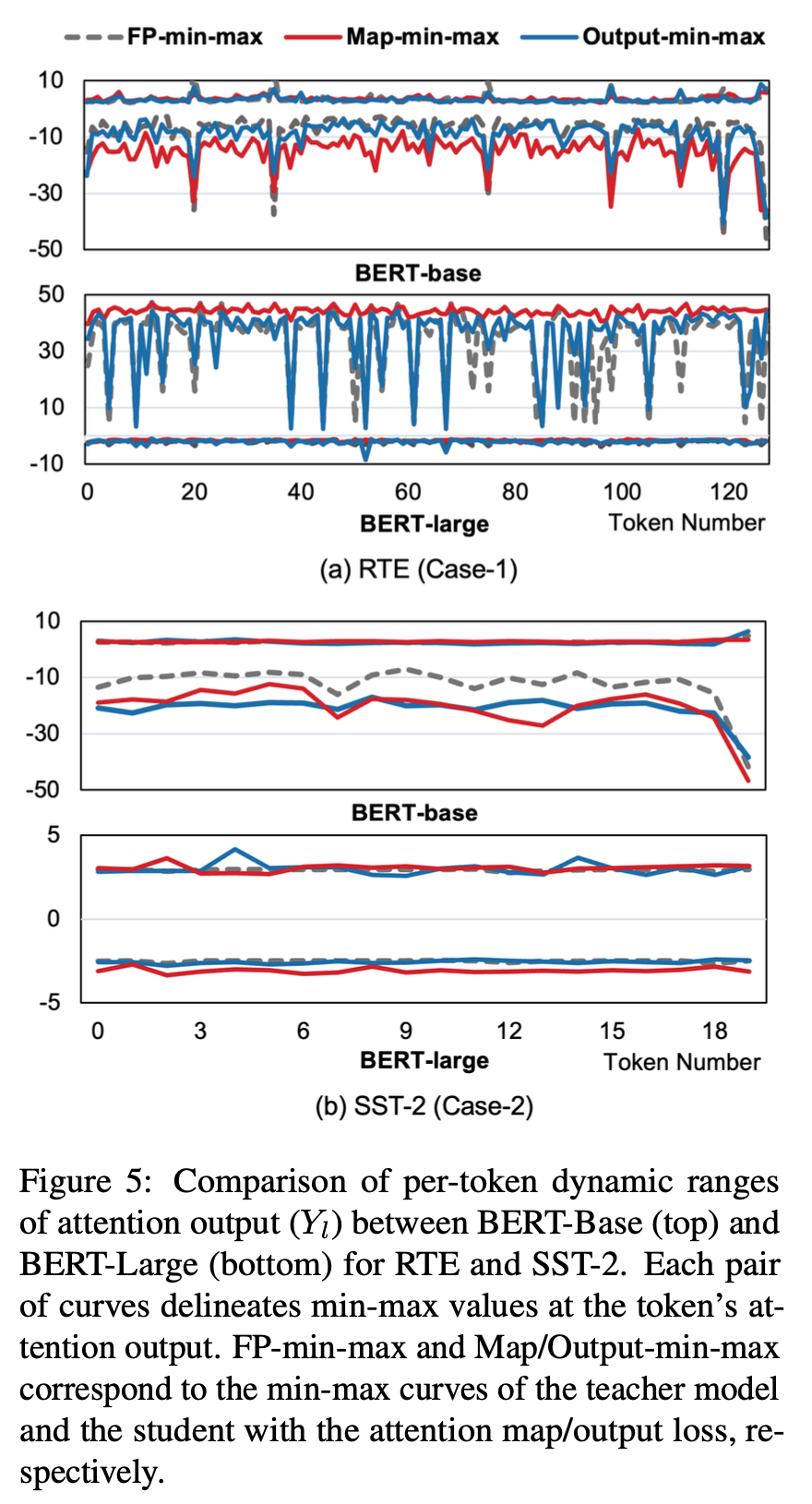
그림 5는 입력 토큰 간의 attention 출력(Yl)의 동적 범위를 나타낸다.

• ( Case - 1 ) RTE와 같이 task에서 특히 특별한 attention 값(특히 토큰에 대한)이 명확한 경우
• ( Case - 2 ) SST-2와 task에서 attention 값이 균일한 경우

모델 크기가 증가함에 따라 각 case의 attention 특성이 더 강조되는 것을 확인할 수 있다.

Recognizing Textual Entailment (RTE)

텍스트 간의 함의(Entailment)를 인식하는 자연어 처리 과제를 가리킨다.

RTE 과제는 두 개의 텍스트 문장이 주어지고, 하나의 문장이 다른 문장을 함의하거나 함의하지 않는지를 판별하는 작업을 다룬다.

주어진 두 문장 간의 관계는 "함의(Entailment)," "모순(Contradiction)," 또는 "중립(Neutral)"으로 분류된다.


함의(Entailment)

두 개의 문장이 주어진 경우, 하나의 문장이 다른 문장의 내용을 반드시 포함하거나 포함하지 않는 관계를 나타낸다.

양자화가 값을 고정하고 굵게 표현하기 때문에 Case-1의 과제에 대한 고유한 attention을 유지하는 것은 어려운 과제다.

• (a) - 상단 : BERT-Base의 경우 attention-map loss는 attention의 차이를 회복하는 데 성공했다.

• (a) - 하단 : BERT-Large의 경우 attention-map loss는 attention을 조절하는 데 실패했다.

attention-map loss가 BERT-Large의 레이어 수가 증가함에 따라 고유한 attention 유지에 실패하는 것으로 추정한다.

SA-GEN 및 SA-PROP의 레이어별 동작을 따로 분석한다.

SA-GEN : self attention probability - a

각 입력 토큰이 자신과 다른 모든 토큰 간의 어텐션 확률을 나타낸다. 이것은 트랜스포머 모델에서 특정 토큰이 다른 토큰에 얼마나 "주의(attention)"를 기울이는지를 나타낸다.

SA-PROP : self attention propagation - f(x)

어텐션 결과가 다음 레이어로 전파되는 과정을 나타낸다. 트랜스포머에서는 어텐션 결과가 여러 레이어를 거쳐 업데이트되며, SA-PROP은 이러한 어텐션 결과의 전파 및 변화를 측정하는 것과 관련이 있다.


BERT-Large의 RTE (Case-1) 및 SST-2 (Case-2)에 대한 특수 토큰 [SEP]의 SA-GEN 및 SA-PROP의 평균 거리를 나타낸다.

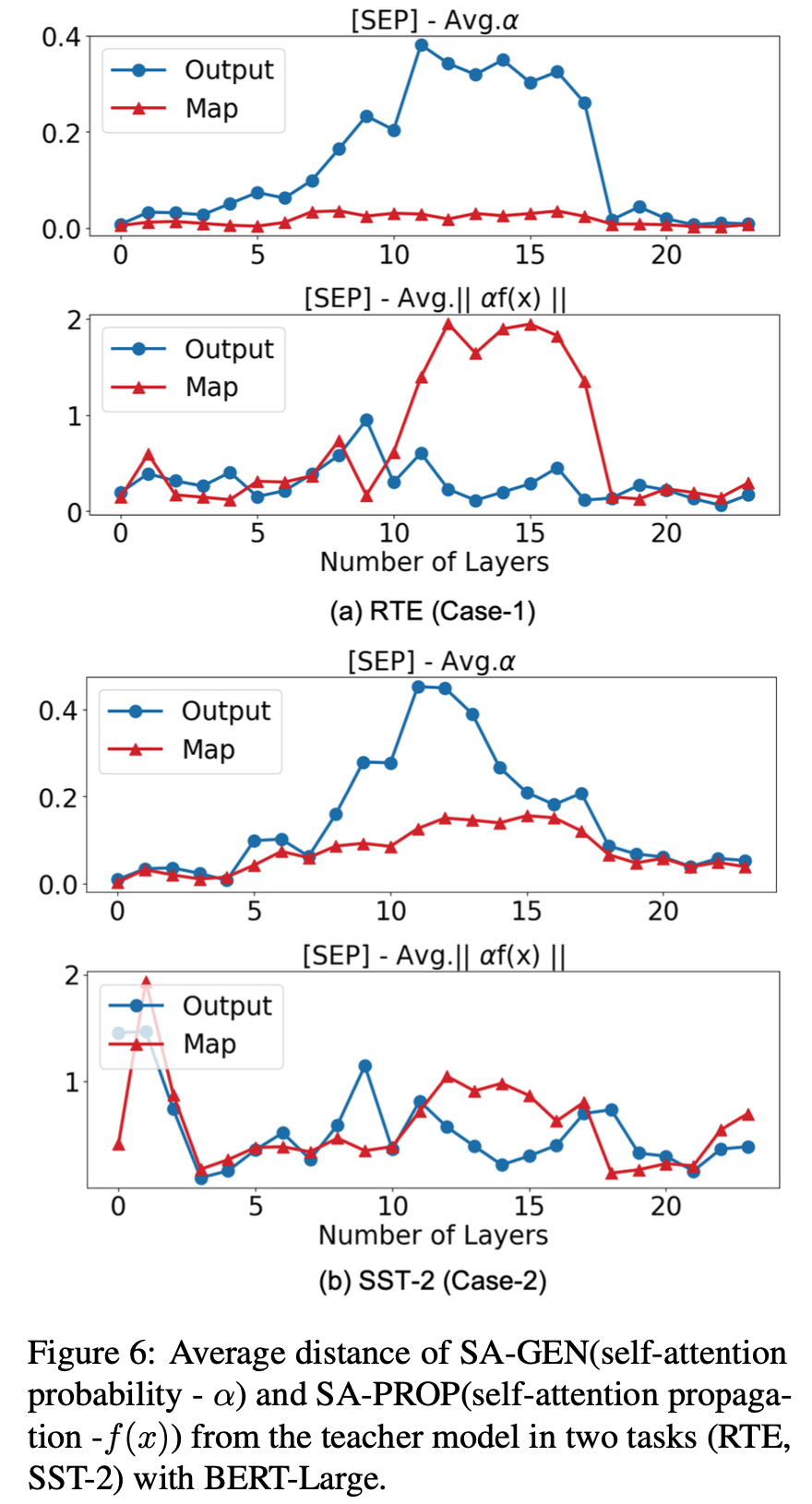
attention-map loss는 SA-GEN의 거리를 억제한다. 이러한 SA-GEN(어텐션 확률)의 억제는 attention 출력을 악화시킨다.

• SST-2의 경우 attention-map loss가 효과적이다.

많은 레이어로 인해 SA-PROP(어텐션 전파)에서의 양자화는 attention-map loss를 통한 KD가 특별한 attention 값을 복구하기에 실패한다.

따라서 SA-PROP(어텐션 전파)에서의 방해를 처리하기 위한 새로운 KD 손실이 필요하다.

Attention Output Loss

SA-PROP의 양자화 오류를 억제하는 한 가지 방법으로 SA-PROP에 직접 KD를 적용할 수 있다. 따라서 새로운 KD 손실인 attention-output loss를 다음과 같이 고안했다.

Fig. 5 (a)에서 볼 수 있듯이 attention-output loss를 사용한 attention 출력은 교사 모델의 고유한 attention을 정밀하게 따른다.

Fig. 6을 통해 attention-output loss의 메커니즘을 이해할 수 있다. attention-output loss는 SA-GEN(어텐션 확률)을 수정하여 결과적인 attention 출력이 교사 모델과 더 잘 일치하도록 조정하게 한다.

SA-GEN의 변경은 Transformer 모델의 상단 레이어에서 발생하므로 attention-output loss는 대형 Transformer 모델에 더 유익하다.

attention-output

어텐션 가중치와 값(value)의 가중 평균이다. 어텐션 가중치는 어텐션 스코어를 정규화한 결과로, 어텐션 출력은 해당 가중치를 기반으로 정보를 종합한 결과다.

💡 attention-score간의 비교가 성능이 좋지 않은 이유는 양자화된 모델에서 어텐션 스코어가 상대적인 중요성을 유지하기 어렵기 때문일 수 있다. 양자화는 가중치 매개변수를 근사화하는 과정으로, 이렇게 근사화된 가중치로 계산된 어텐션 스코어는 정확도를 유지하기 어렵게 만들 수 있다. 따라서 어텐션 스코어를 비교하는 것은 성능에 부정적인 영향을 미칠 수 있다.

💡 그러나, attention-output에 대한 비교는 교사 모델과 학생 모델의 최종적인 예측 결과의 차이를 줄여주며, attention-score에 비해 양자화에 대한 민감도가 낮다고 볼 수 있다.

💡 따라서, attention-output과 attention-score 모두 attention-map처럼 개별적인 대상에 대한 비교가 아닌 합을 통한 최종 결과에 대한 비교이기 때문에 MSE를 사용하지만 attention-output은 성능을 향상시키는 데 도움을 줄 수 있다.

과제 종속적 특성을 더 잘 이해하기 위해 attention-output loss가 attention map의 self-attention 확률에 미치는 영향을 경험적으로 관찰한다.

attention map의 수정을 정량화하기 위해 각 헤드별로 개별 토큰의 attention 확률 순위를 정규화한 Ranking ratio를 도입했다.

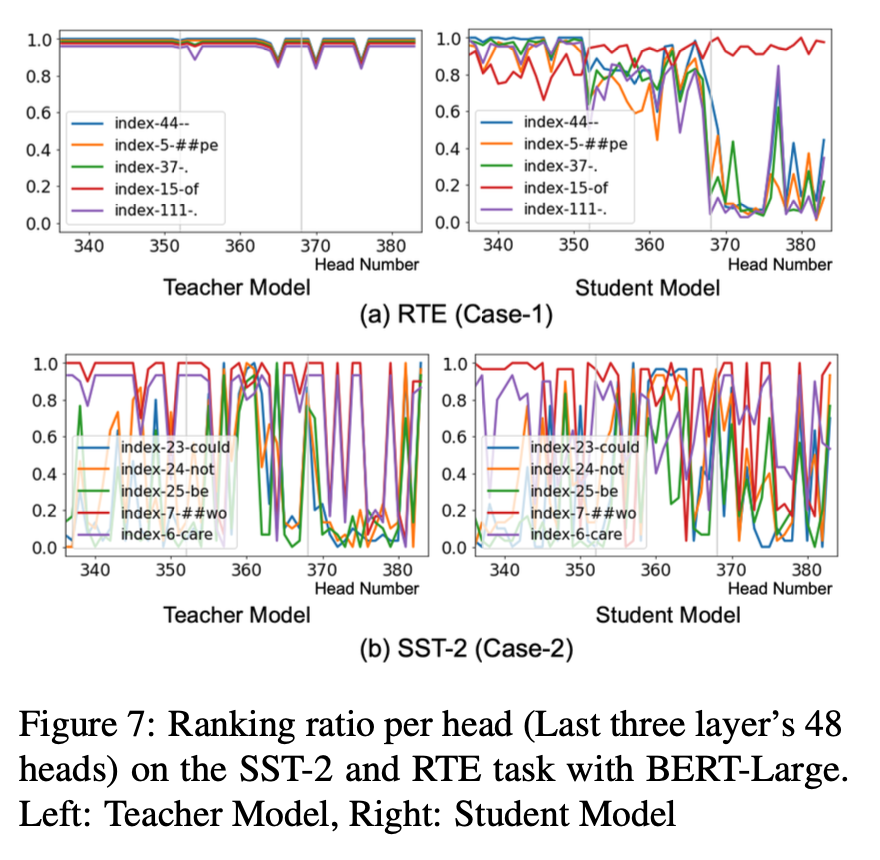
Fig. 7은 선택된 토큰의 Ranking ratio를 전체 정밀도를 가진 교사 모델과 양자화된 학생 모델 각각의 헤드별로 비교한다.

• ( Case - 1 ) RTE의 경우 : attention-output loss를 사용한 QAT는 loss가 감소하는 특정 방향으로 랭킹을 빠르게 변경한다.

• ( Case - 2 ) SST-2의 경우 : 선택한 토큰의 순위는 QAT에 관계없이 크게 변경된다. 따라서 attention 출력에 대한 KD는 의미 있는 방향으로 순위를 조절할 수 없다는 것을 확인했다.

Unified Attention-Map and Output Loss

BERT-Large의 task-dependent 어텐션 특성을 고려하여 QAT에 대한 어텐션 맵 및 출력 손실을 통합한다.

어텐션 맵과 출력 손실 사이의 선호도는 모델 크기 및 과제에 따라 다양하다.

탐구를 위해 다음과 같이 혼합 매개변수인 γ를 사용하여 통합 어텐션 맵 및 출력 손실을 고안한다.

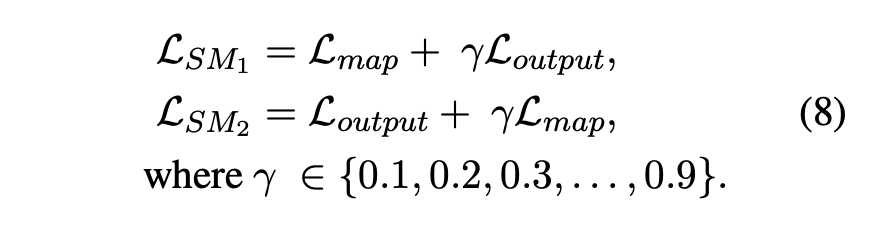
통합 손실은 최적의 성능을 내는 KD 손실 (어텐션 맵 또는 출력 손실)의 정확도를 향상시킬 수 있다.

---

Conclusion

이 연구에서는 대규모 트랜스포머에 대한 QAT의 KD 메커니즘을 조사했다.

attention-map 및 attention-output 손실이라는 두 가지 KD 방법을 제안하여 self-attention 정보를 더 잘 복원하도록 했다.

다양한 트랜스포머 인코더 모델에서의 실험 결과는 제안된 KD 방법과 그들의 결합이 sub-2-bit 가중치 양자화에 대한 최고 수준의 정확도를 달성한다는 것을 보여준다.

---

Limitation

이 연구는 KD가 Transformer 인코더에 대한 QAT에 어떻게 작용하는지를 조사했다.

이 작업에서 사용된 분석 기술은 많은 흥미로운 통찰력을 나타내지만, KD 하에서 양자화의 영향을 이론적으로 더 분석하는 것이 높이 평가될 것이다.

또한, 두 가지 제안된 KD 기술을 통합하는 가능성을 탐색하였으며, 두 개 이상의 KD 손실을 자동으로 균형있게 통합하는 것은 흥미로운 향후 연구 방향이 될 수 있다.