손실함수(loss function)
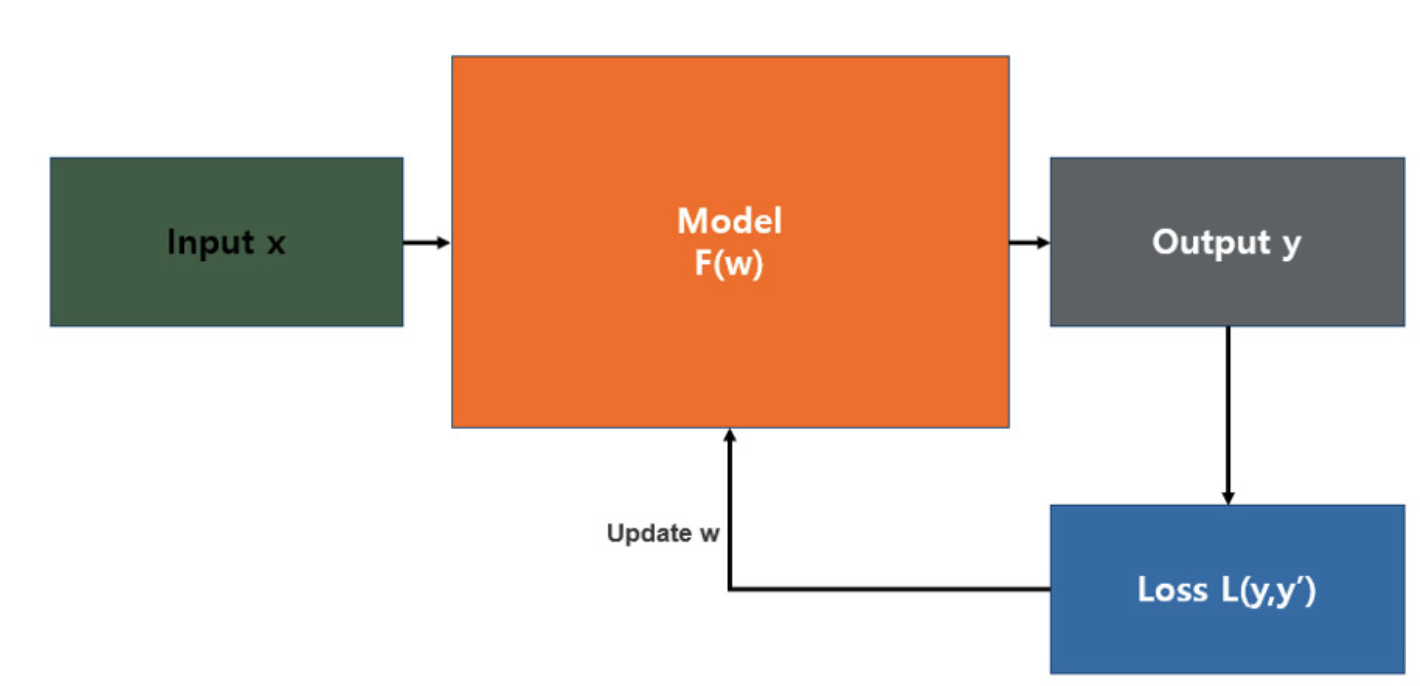
손실함수 혹은 비용함수(cost function)는 같은 용어로 통계학, 경제학 등에서 널리 쓰이는 함수로 머신러닝에서도 손실함수는 예측값과 실제값에 대한 오차를 줄이는 데에 유용하게 사용된다.
위의 그림은 일반적인 통계학의 모델로, 입력값(x)를 함수 (F(w))에 넣었을 때 결과값(y)가 나오는 것을 그림으로 그린 것이다. 그렇다면 예측값으로 나온 y와 실제의 y값(y')이 유사할수록 모델이 좋다고 할 수 있을 것이다. 이 때, 예측값과 실제값의 차이를 확인하는 함수가 바로 손실함수이다.
손실함수는 측정한 데이터를 토대로 산출한 모델의 예측값과 실제값의 차이를 표현하는 지표이다. 즉, 모델이 데이터를 얼마나 잘 표현하지 못하는가를 나타내는 지표라고 할 수 있다. 따라서 얼마나 잘 표현하지 못하는가를 어떤 방식으로 표현하느냐에 따라 다양한 손실함수가 존재한다
손실함수의 종류
인공지능은 인간의 사고하는 방식을 모방하는 것보다 인간이 해결하고자 하는 문제를 효율, 효과적으로 해결하는 데에 초점을 맞춘다. 즉 어떠한 문제를 해결하고자 하는가에 따라 적합한 손실함수를 설정해야 좋은 결과를 얻을 수 있다는 것이다. 손실함수에는 다양한 종류들이있지만 이중 몇 가지를 선정하여 간략하게 정리해보고자 한다.
회귀 모델에 쓰이는 손실함수에는 MSE, MAE, RMES 등이 있으며
분류 모델에 쓰이는 손실함수에는 Binary cross-entropy, Categorical cross-entropy 등이 있다.
일반적으로 신경망 학습에서는 평균제곱오차(MSE)와 교차 엔트로피 오차(cross entropy error)를 사용한다고 한다.
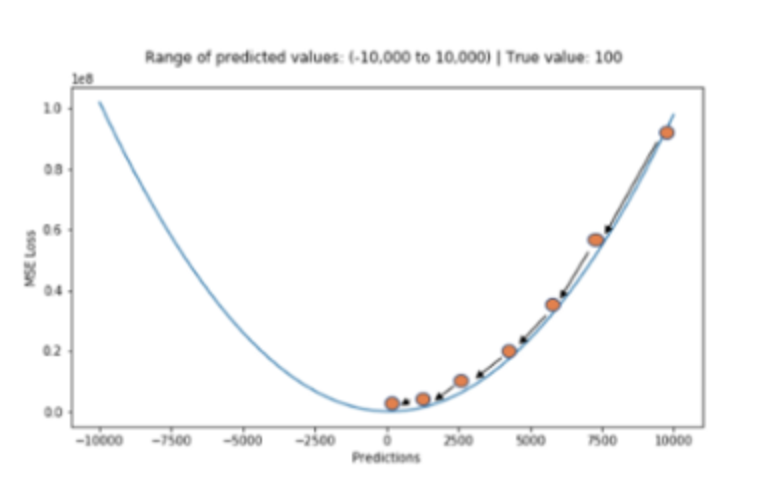
MSE(Mean Square Error)

-
장점:
실제 정답에 대한 정답률의 오차뿐만 아니라 다른 오답에 대한 정답률의 오차도 포함하여 계산해준다.
MAE와 달리 최적값에 가까워질수록 이동값이 다르게 변화하기 때문에 최적값에 수렴하기 용이하다. -
단점:
값을 제곱하기 때문에 절댓값이 1미만인 값은 더 작아지고, 1보다 큰 값은 더 커지는 왜곡이 발생할 수 있다.
제곱하기 때문에 특이값의 영향을 많이 받는다.
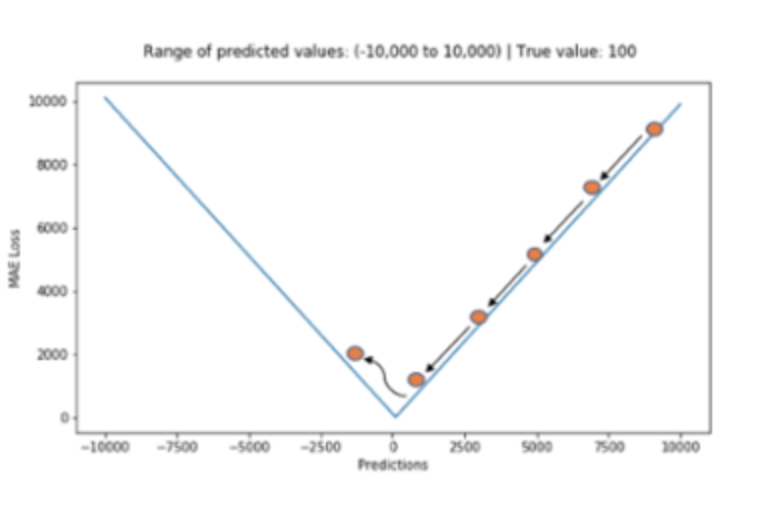
MAE(Mean Absolute Error)
-
장점:
전체 데이터의 학습된 정도를 쉽게 파악할 수 있다. -
단점:
어떤 식으로 오차가 발생했거나 음수인지 양수인지 알 수 없다.
위의 그림에서처럼 최적값에 가까워졌다고 하더라도 이동거리가 일정하기 때문에 최적값에 수렴하기 어렵다.
entropy
엔트로피는 불확실성의 척도이다.
본래 물리학에서 분자들의 무질서도 혹은 에너지의 분산 정도를 나타내는 용어인데 여기에서 착안하여 정보학에서 엔트로피는 정보의 양으로서 신호를 인식하는 데에 쓰인다고 한다.
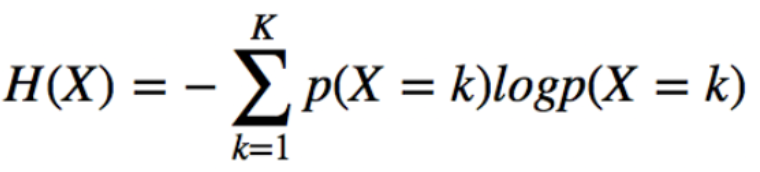
엔트로피가 정보(information)학에서 쓰이게 되면 정보량의 기댓값을 의미한다고 할 수 있다. 즉, 어던 확률분포로 일어나는 사건을 표현하는 데에 필요한 정보량을 의미한다. 여기에서 말하는 엔트로피는 확률 분포의 무질서도나 불확실성, 혹은 정보 표현의 부담 정도를 나타내는 것이다.
정보는 신호에 존재하는 정보의 양으로 비교할 수 있는데 정보의 양은 누구나 알만한 정보가 아닌 새롭고 특이해서 사람들을 놀라게 만드는 정도가 클수록 많다라고 볼 수 있다고 한다.
내일 친구가 밥을 먹는다는 것은 충분히 예상할 수 있지만 내일 친구가 놀이동산을 간다고한다면 예상하지 못해 내게 놀라움을 주니 정보량이 더 크다고 할 수 있다.
P(x)는 x라는 사건이 발생할 확률, I(x)는 x의 정보량을 의미한다고 한다면 아래와 같은 특성을 가지고 있다.
- 불확실성이 클수록 정보의 양은 크다. 이라면
- 두 개의 별개의 정보량은 각 정보량의 합과 같다.
두 개의 독립적인 사건의 발생확률은 로 표현되는데 정보량은 합산이기 때문에 이를 만족시키기 위해 log를 씌워주어 주는 것이다. 즉, 가 된다. - 정보량은 bit로 표현된다. (로그가 2인 이유를 생각해봐야할 듯.)
Cross entropy 교차엔트로피
정보 엔트로피는 하나의 확률분포가 갖는 불확실성(놀람의 정도) 혹은 정보량을 정량적으로 계산할 수 있도록 하는 개념이다.
교차 엔트로피는 두 가지 확률 분포가 얼마나 비슷한지를 수리적으로 나타내는 개념이다.
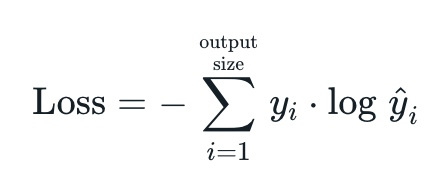
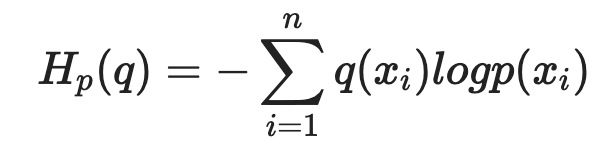
크로스엔트로피는 실제 분포 q에 대해서 알지 못하는 상태에서 모델링을 통해 구한 분포인 p를 통해 q를 예측하는 것이다. q와 p가 모두 들어가기 때문에 교차 엔트로피라고 불린다고 한다.
q는 딥러닝 모델의 추정 확률분포를, p는 딥러닝 모델이 추구해야할 미지의 확률분포를 의미한다.
이 q와 p를 활용하여 교차 엔트로피를 계산하여 이 교차 엔트로피가 낮아지는 쪽으로 모델의 추정 확률분포 q를 꾸준히 개선하여 확률분포 q를 확률분포 p에 가깝게 접근시켜나갈 수 있다. (이 특성이 이진분류에서 신경망을 학습시킬 수 있는 원리가 된다고 한다.)
크로스엔트로피에서는 실제값과 예측값이 맞는 경우에는 0으로 수렴하고 값이 틀릴 경우에는 값이 커지기 때문에 두 확률분포가 서로 얼마나 다른지를 나타내주는 정량적인 지표 역할을 한다.
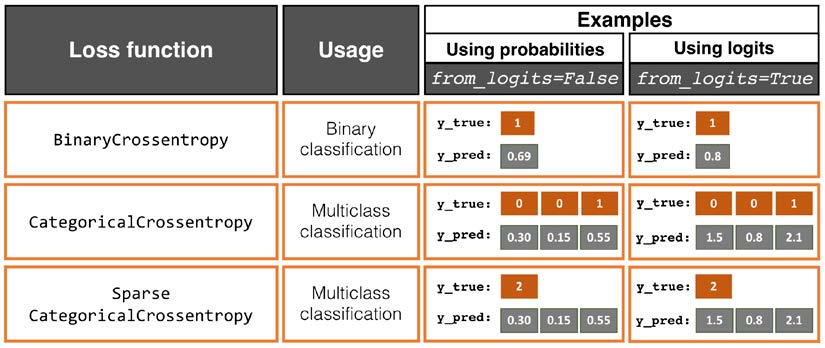
Binary Crossentropy
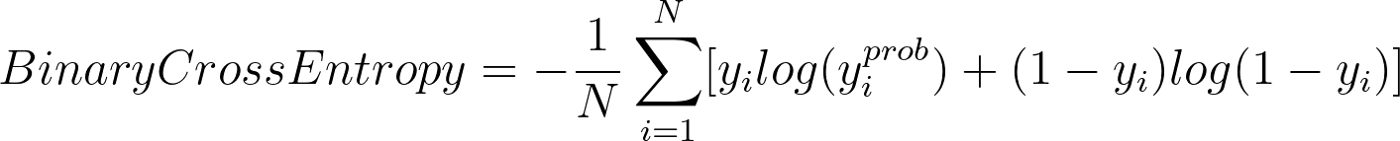
만약 이진 분류기를 훈련한다면 binary crossentropy 손실함수를 사용하는 것이 적절하다.
이진 분류기는 true/false, 양성/음성처럼 2개의 클래스로 분류할 수 있는 분류기를 의미한다.
(0과 1만 가지는 확률변수는 베르누이라고도 불린다.)
손실함수는 예측값과 실제값이 같으면 0이 되는 특성을 갖고 있어야 한다.
이진분류기의 경우 예측값이 0과 1 사이의 확률값으로 나온다. 0에 가까울수록, 1에 가까울수록 둘 중 한 클래스에 가깝다는 것이다.
(logistic regression에서 보는 cost function은 cross entropy의 시그마를 풀어쓴 것과 같다..)
Categorical Crossentropy

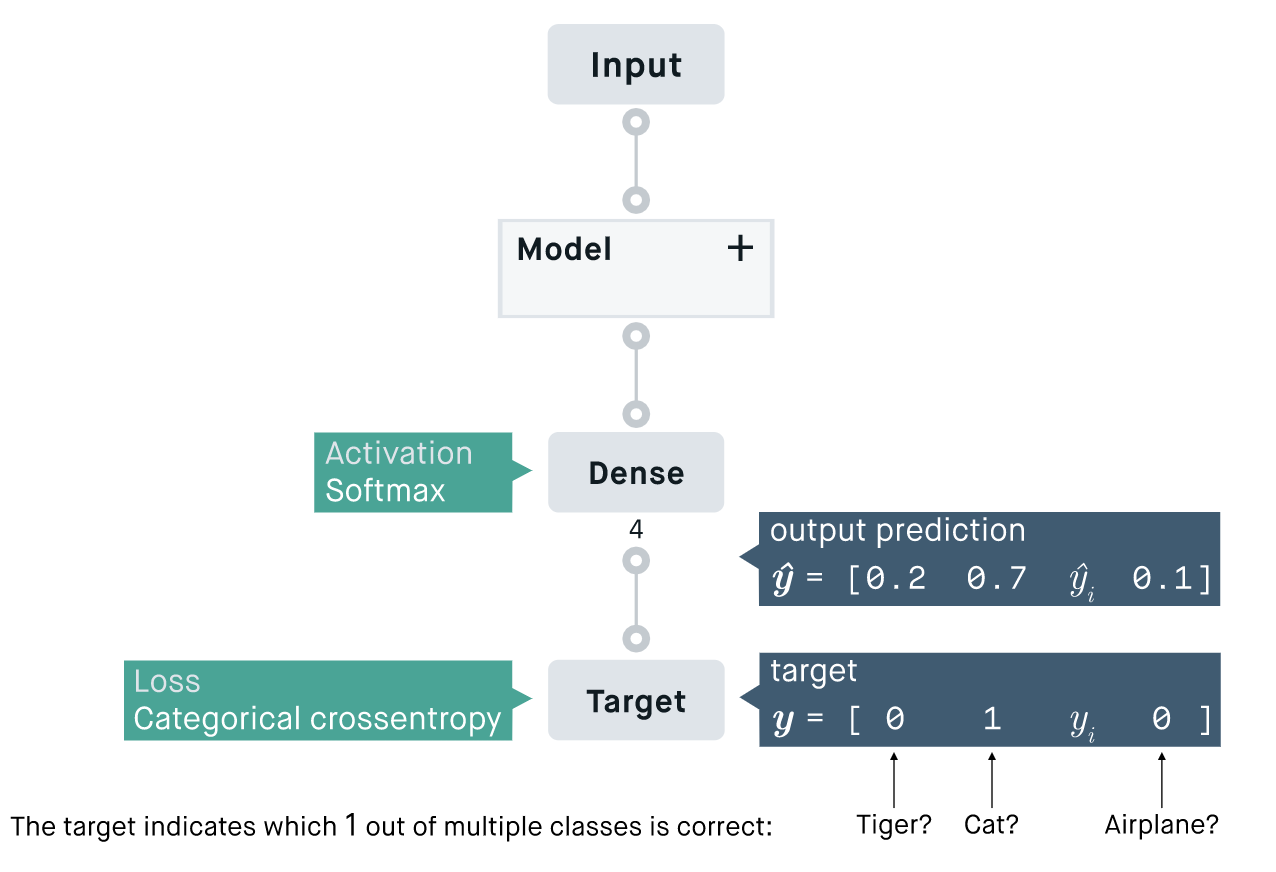
Categorical Crossentropy는 분류해야할 클래스가 3개 이상인 경우에 사용된다. (멀티클래스 분류라고도 하는 것 같다.)
라벨이 one-hot encoding의 형태로 제공될 때 사용되는 것으로 보인다.
softmax 활성함수와 함께 쓰이는 경우가 많아 softmax activation function이라고도 불린다.
Sparse Categorical Crossentropy
Sparse Categorical Crossentropy는 분류해야할 클래스가 3개 이상이며 라벨이 0, 1, 2처럼 정수의 형태로 제공될 때 주로 사용된다.
참고 블로그 1
참고 블로그 2_ 엔트포리와 교차 엔트로피
Categorical Crossentropy
다양한 손실함수들
표
