ANN(Artificial Neural Networks)

ANN, 즉 인공 신경망은 실제 신경계의 특징을 모사하여 만들어진 계산모델이다.
인공 신경망의 기본 구조인 퍼셉트론은 인간의 뇌 신경망의 기본 구조인 뉴런을 모사하여 제작되었는데 최근에는 ANN과 뉴런을 줄여서 Neural-net(뉴럴넷)으로 많이 불리고 있다고 한다.

뉴런의 구조

아무래도 뉴런의 구조를 모사하여 퍼셉트론, 더 나아가 ANN을 만들었다보니 뉴런의 구조를 조금이나마 파악하면 이해가 더 쉬울 것이다.

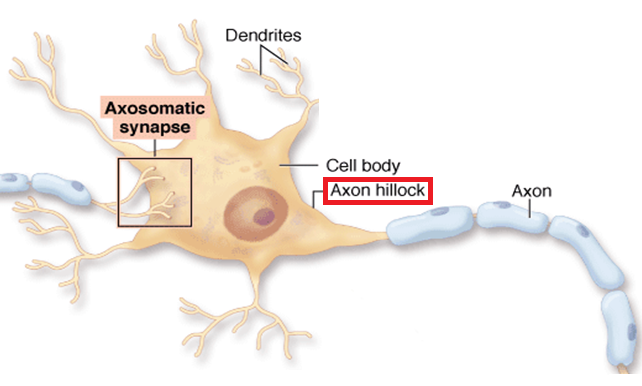
위의 사진이 신경세포(Neuron)이다.
수상돌기라고 불리는 dendrites에서 입력신호를 다른 뉴런으로부터 받아들인 뒤 그 신호를 신경세포 내에서 통합한다. 이 때 임계값을 넘어서는 전류가 생기면 Axon Hillock이 축삭돌기(Axon)로 최종 출력 신호를 전송하여 다음 뉴런으로 전파한다고 한다.

이러한 구조를 바탕으로 퍼셉트론이 만들어졌고 이러한 퍼셉트론이 모여 신경망이 만들어진다.

신경망의 기본 형태: 가중치, 편향 연산

인공 신경망은 생물의 신경 세포를 모사하여 만들어졌다.
이러한 인공 신경망의 목표는 생물의 신경망과 유사한 인공 신경망을 만드는 것이 아니라 복잡한 데이터 속에서 패턴을 발견할 수 있는 알고리즘으로서의 인공 신경망을 만드는 것이다.

뉴런을 모사한 퍼셉트론으로 이루어진 신경망의 기본 형태를 도식화하면 아래와 같다.

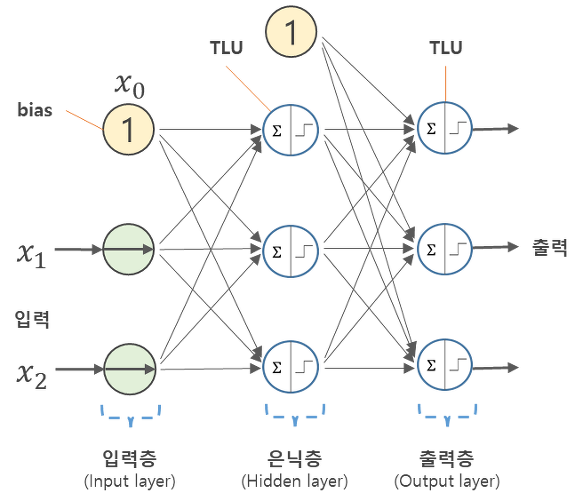
위 그림에서 원으로 표현된 부분은 뉴런 혹은 노드라고 불린다.
노드는 입력되는 벡터 중 하나를 의미하며 각각 하나씩을 지칭할 때 노드라는 이름을 쓴다.

노드의 역할

노드의 역할은 세 단계로 구성된다고 할 수 있다.
1. 입력 신호($x_0,x_1,...,x_n$)가 입력되면 각각 고유한 가중치($w_0, w_1,...,w_n$)가 곱해진다.
2. 다음 노드에서 입력되는 모든 신호를 더해준다. ($\sum$)
3. 각 노드에서의 연산값이 정해진 임계값(Threshold Logic Unit)을 넘을 경우에만 다음 노드들이 있는 층(layer)으로 신호를 전달한다.

🍎 활성화 함수(Activation Function)

3번에서 연산값이 정해진 임계값을 넘을 경우에만 다음 노드들이 있는 층으로 신호를 전달한다고 한다. 이렇나 역할을 하는 것이 바로 활성화 함수이다.
가장 간단한 활성화 함수인 3개 (Step, Sigmoid, ReLu)를 정리해보도록 한다.

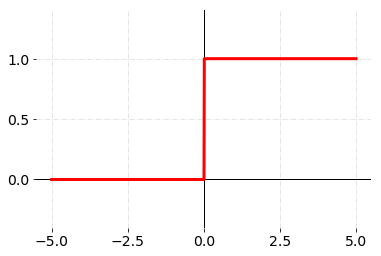
계단 함수(Step function)

계단 함수는 입력 값이 임계값(여기서는 0)을 넘기면 1을 출력하고, 그렇지 않으며 0을 출력하는 함수이다.
계단 함수의 그래프는 아래의 그림과 같다.

시그모이드 함수(Sigmoid function)

신경망이 경사 하강법을 통해 학습을 진행하기 위해서는 미분을 해야한다.
하지만 계단함수는 임계값지점에서 미분이 불가능하고 나머지 지점에서는 미분값이 0이 나온다.
따라서 실제 계단함수를 활성화함수로 사용하면 학습이 제대로 이루어지지 않는다.
시그모이드 함수는 이러한 계단함수의 단점을 해결하기 위해 사용된 함수이다.

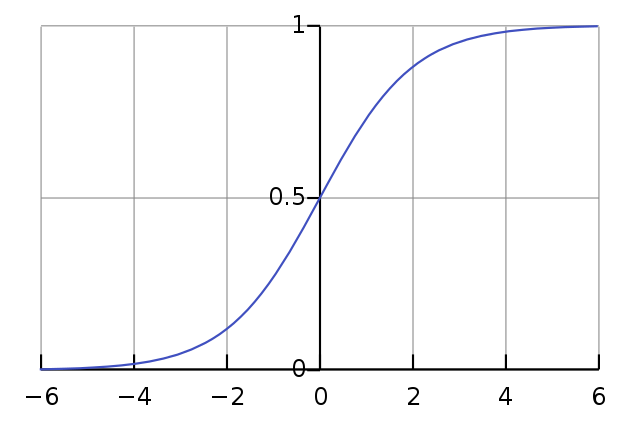
계단함수처럼 임계값(0)보다 작은 부분은 0에 가까워지고 큰 부분은 1에 가까워진다.
하지만 조금 더 부드럽게 연결되어 있기 때문에 모든 지점에서 미분 가능하며 미분값도 0이 아니다.

ReLU 함수

ReLU함수는 실제로 많이 사용되는 활성화 함수이다.

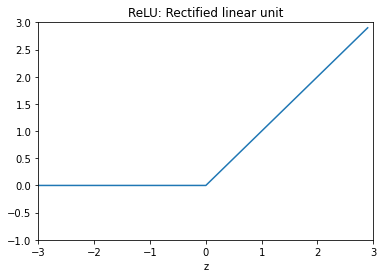
신경망의 각 층

THE NEURAL NETWORK ZOO

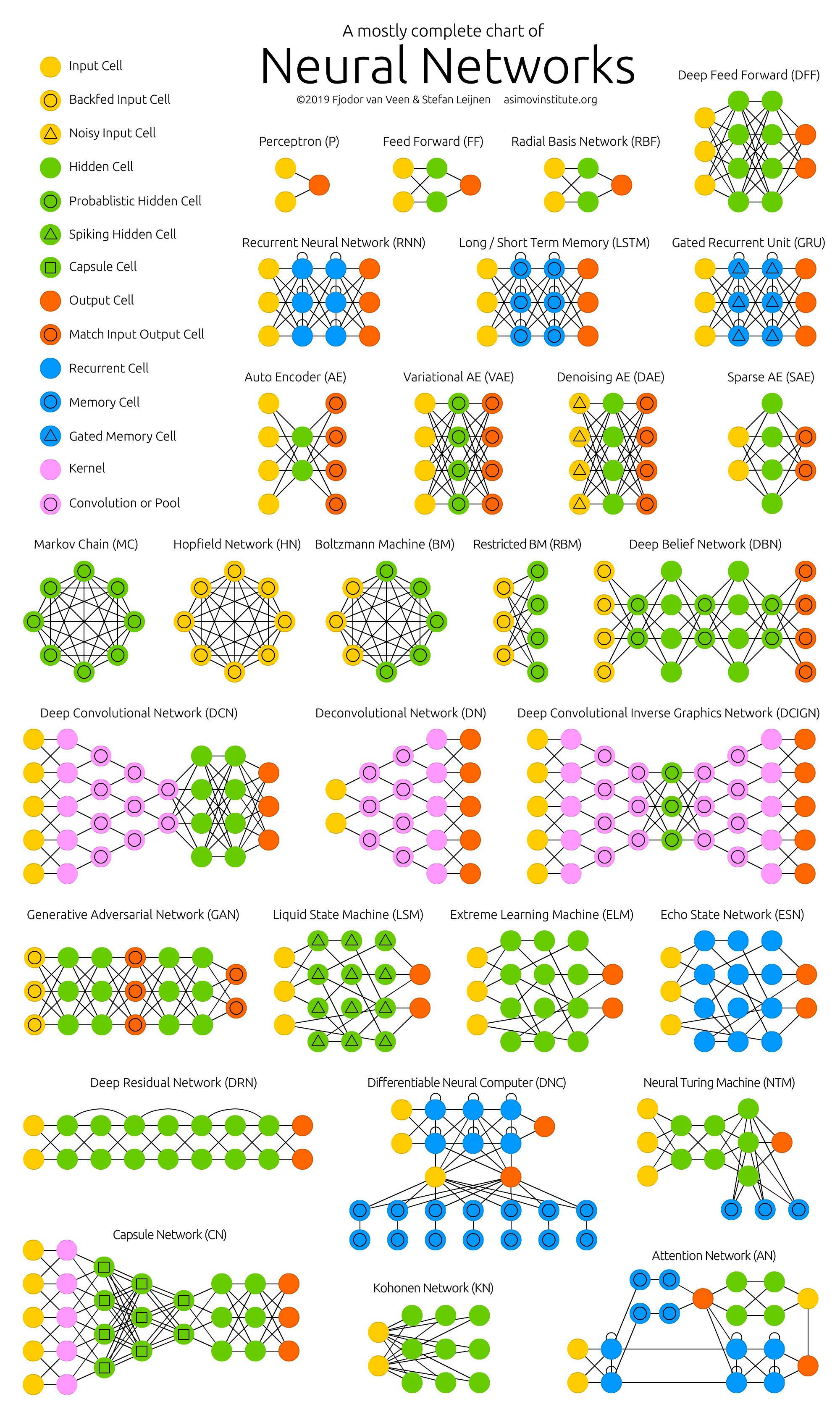
실무에서는 위와 같이 매우 다양한 신경망들이 쓰인다. 복잡하게 생긴 신경망들의 각각의 장단점도 있지만 공통적인 구조도 가지고 있다.

신경망은 크게 세 가지 층으로 나눌 수 있다.
아래이 그림처럼 입력층, 은닉층, 출력층으로 나뉜다고 한다.

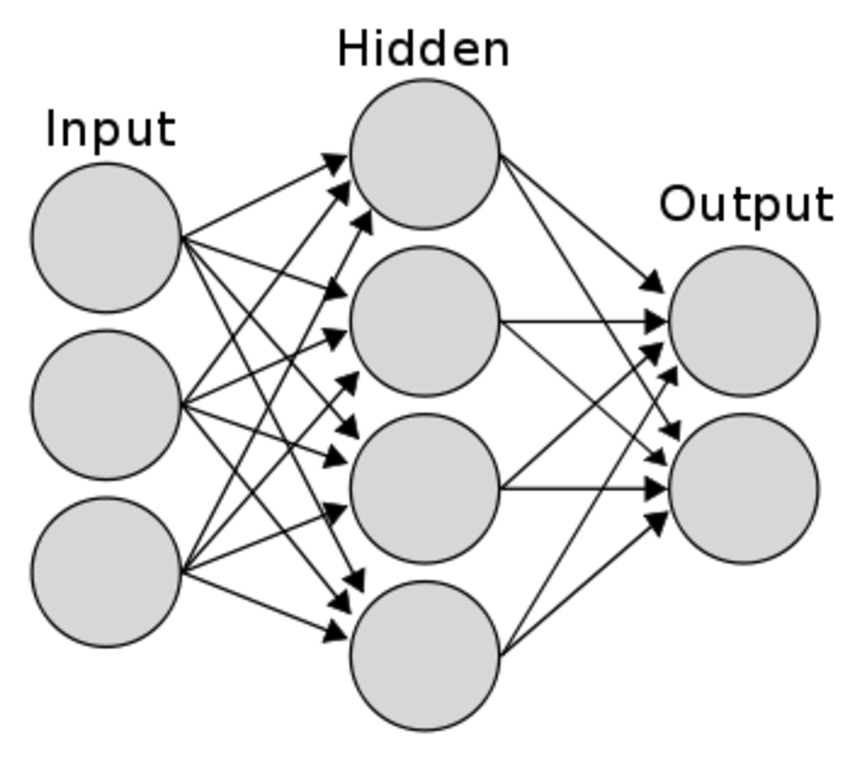
💛 입력층(input layer)

입력층은 데이터셋이 입력되는 층이다.
입력층은 입력되는 데이터셋의 특성(feature)에 따라 노드의 수가 결정된다.
보통 입력층은 어떠한 계산을 수행하지 않고 그냥 값들을 전달하기만하면 된다.
그렇기 때문에 신경망의 층수(깊이, depth)를 셀 때 입력층은 포함하지 않는다.

💛 은닉층(Hidden layer)

은닉층은 입력층으로부터 입력된 신호가 가중치, 편향과 연산되는 층이다.
일반적으로 입력층과 출력층 사이에 있는 층을 은닉층이라고 한다.
은닉층은 블랙박스모델처럼 사용자가 은닉층 내에서 일어나는 계산의 결과를 볼 수 없기 때문에 은닉층이라는 이름으로 불린다. 은닉층은 입력 데이터셋의 특성 수와 상관없이 노드 수를 구성할 수 있다.

일반적으로 딥러닝(deep learning)이라고 하면 2개 이상의 은닉층을 가진 신경망을 의미한다.
은닉층의 수가 늘어나고 더 좋은 학습 방법이 개발되면서 복잡한 데이터의 구조를 학습할 수 있게 되었는데 이렇게 복잡한 신경망이 다른 알고리즘이 세웠던 성능을 갱신하면서 딥러닝이 지금의 주목을 받았다.

💛 출력층(Output layer)

출력층은 가장 마지막에 위치한 층으로 은닉층 연산을 마친 값이 출력되는 층이다.
신경망 모델에서 출력값을 의미하며 이 출력층의 노드 개수, 모양에 따라 모델의 정의가 달라질 수 있다.
사용자가 해결해야할 문제에 따라서 출력층을 잘 설계하는 것이 중요하다.
출력층은 아래처럼 구성될 수 있다.

⭐️ 이진분류(binary classification)

활성화 함수로는 시그모이드 함수를 사용하며 출력층의 노드 수는 1로 설정한다.
출력되는 값은 0과 1 사이의 확률값이 되도록 한다.

⭐️ 다중분류(Multi-class Classification)

활성화 함수로는 소프트맥스(Softmax) 함수를 사용하며 출력층의 노드 수는 레이블의 클래스(Class) 수와 동일하게 설정한다.

⭐️ 회귀(Regression)

일반적으로는 활성화 함수를 지정해주지 않으며 출력층의 노드 수는 출력값의 특성(Feature) 수와 동일하게 설정한다. 만약 특정한 하나의 값을 예측하는 문제라면 1로 설정해주면 된다.

신경망 구현하기

아주 간단한 신경망을 구현해보고자 한다.
구현하고자 하는 신경망은 아래와 같다.

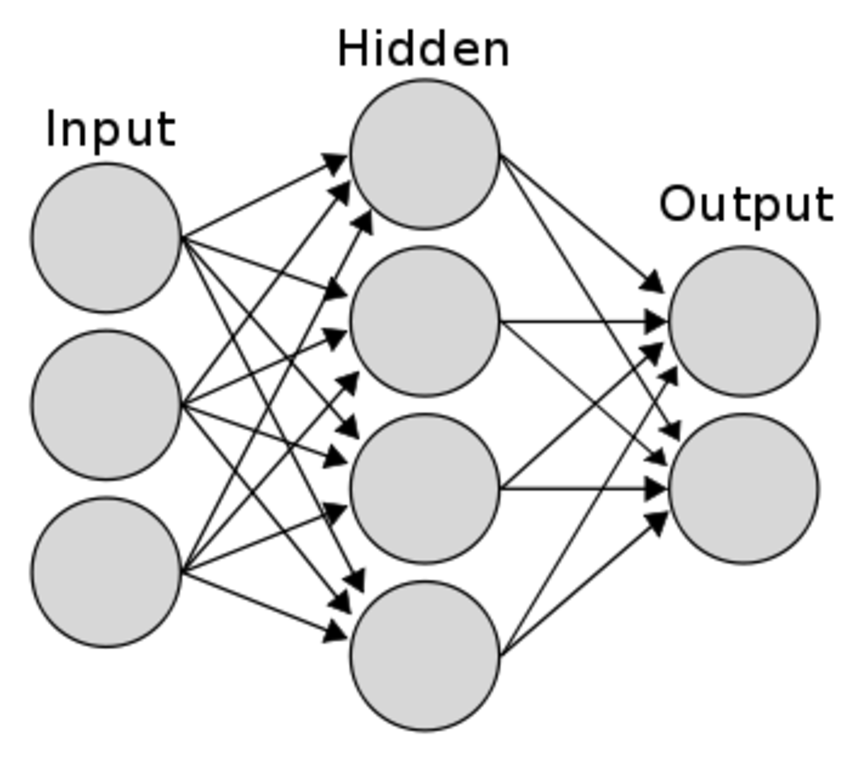
1️⃣ 초기 상태 설정하기

shape을 주의깊게 살펴본다.
행렬곱의 원리를 생각하면서 어떤 shape을 가진 값들을 받는지 확인해야한다.
아래는 네트워크 구조를 생성하는 함수를 정의하는 함수이다.
가중치와 편향의 임의의 값이다.

#네트워크 구조 생성 함수 정의
def init_network():
    network = {}
    network['W1'] = np.array([[0.1,0.3,0.5, 0.7],[0.2,0.4,0.6,0.8],[0.9,0.8,0.7,0.6]]) ##3x4행렬
    network['B1'] = np.array([0.11,0.12,0.13,0.14])
    network['W2'] = np.array([[0.1,0.5],[0.2,0.8],[0.3,0.9],[0.4,0.8]]) ##4x2행렬
    
    return network

2️⃣ 순전파(Feed Forward) 함수를 정의한다.

순전파는 가중치(W)와 편향(B)의 연산을 반복하며 입력값을 받아 출력값으로 반환하는 과정이다.

#순전파 함수 예시
def forward(network, x):
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['B1'], network['B2']
    
    a1 = np.dot(x, W1)+b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2)+b2
    
    return a2

forward 함수에서 network는 가중치와 편향이므로 위 함수는 가중치와 편향의 연산을 반복하기 위한 함수이다.

🍏 np.dot()
딥러닝 신경망에서 행렬의 곱으로 신경망 연산을 할 때 np.dot() 함수를 쓰곤 한다.
이 함수는 두 행렬의 내적합, 즉 행렬의 곱셈식을 계산할 대 사용한다.(실수 등을 곱해도 된다.)

#np.dot 예제
import numpy as np

a=np.array([3,4])
b=np.array([4,5])
np.dot(a,b)

3️⃣ 정의한 함수와 입력 데이터를 바탕으로 계산한 값을 출력하기

#네트워크 제작
network = init_network()

#샘플 입력 데이터
x = np.array([1, 0.5, 0.7])

#순전파 실행
y = forward(network, x)

print(y)

위의 과정은 학습없이 입력 값에 가중치를 연산하여 출력을 내는 것으로 한 번의 순전파가 일어나는 간단한 신경망이다. 위와 같은 신경망에서 가중치 행렬과 입력 신호의 연산이 어떻게 일어나는지 도식을 통해 살펴볼 수 있다.

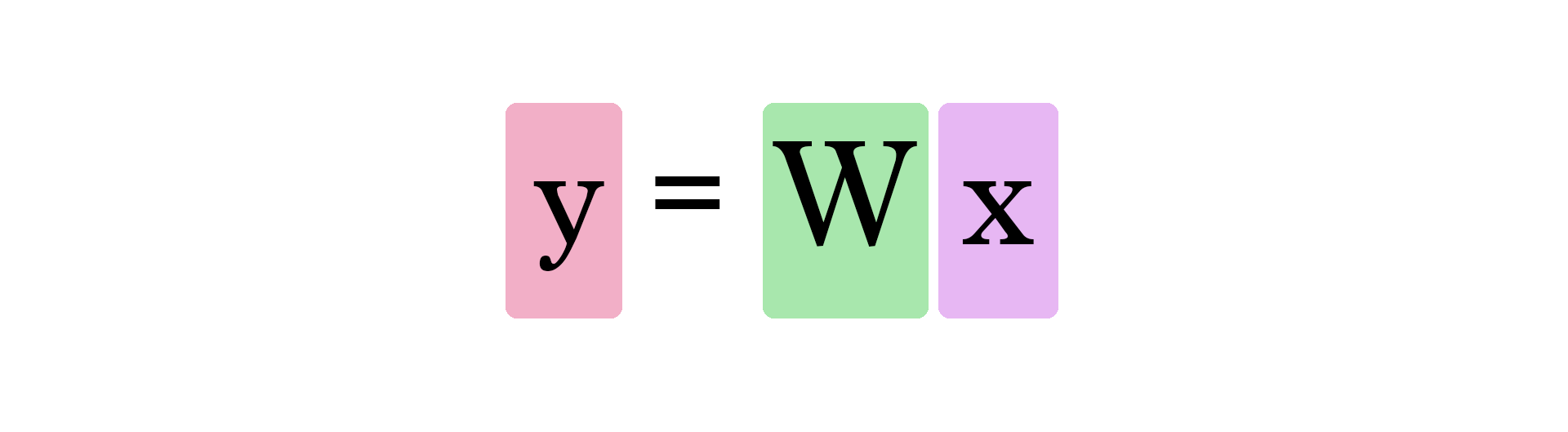
x는 입력된 값 혹은 벡터, W는 가중치, y는 가중치가 연산된 x로 순전파가 일어난 결과값이다.

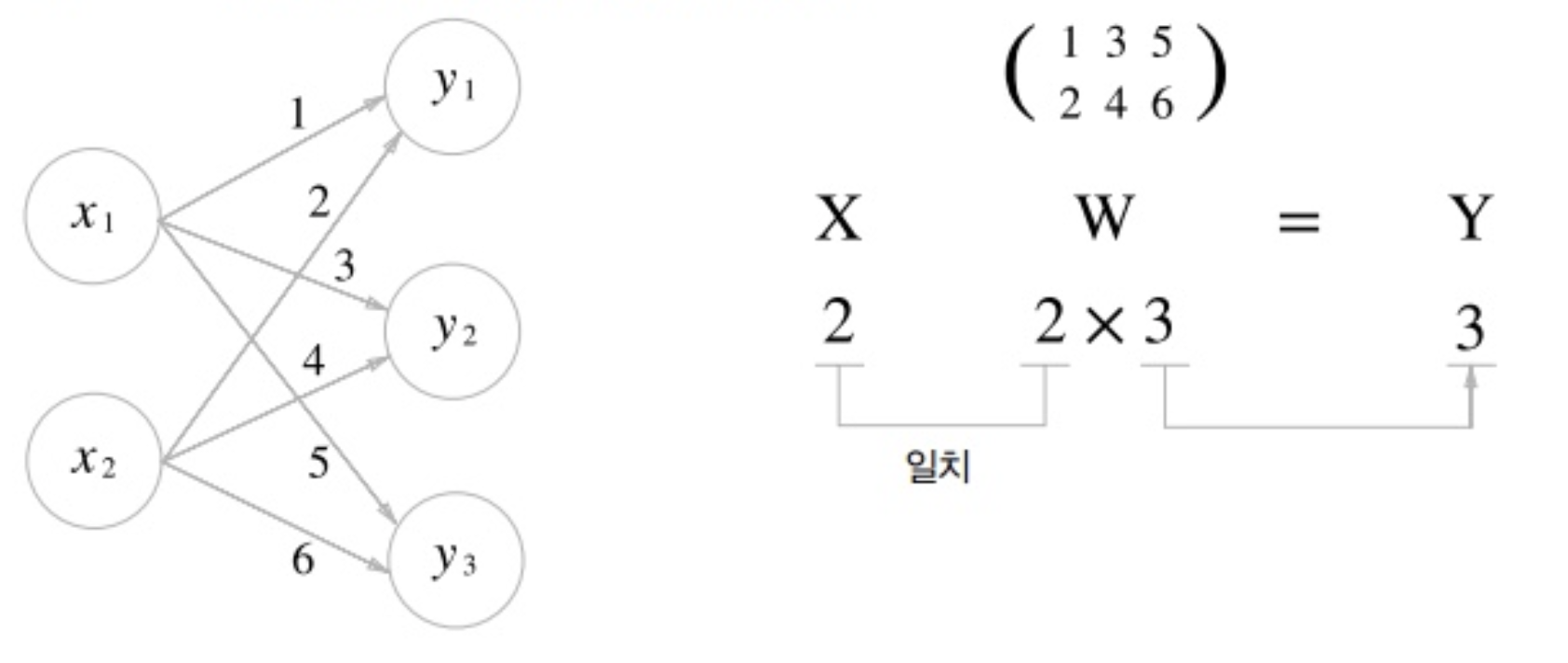
위처럼 신경망은 노드가 가중치로 연결되어 입력신호와 연산된 뒤 출력값으로 내보내는 함수라고 할 수 있다.
가중치를 지속하여 수정하면서 적절한 가중치를 찾는 과정을 학습(Training, Learning)이라고 한다.

❓ 각 레이어의 노드 개수는 어떻게 정해지는가?
❓ 가중치의 초기값을 어떻게 설정하는가?
가중치는 학습을 시작하기 전 초기값은 모두 같은 값으로 설정한다.