DuoGuard: A Two-Player RL-Driven Framework for Multilingual LLM Guardrails

Introduction

• 영어 외 언어에 대해서는 공개된 안전 데이터가 많지 않아 다국어 가드레일 모델의 종류 및 성능 또한 제한됨
• 생성자와 가드레일 모델 간 적대적 훈련을 통해 고품질의 합성 데이터를 생성하는 2-Player 강화 학습 프레임워크 DuoGuard 제안

Methodnology

1. 가드레일 모델
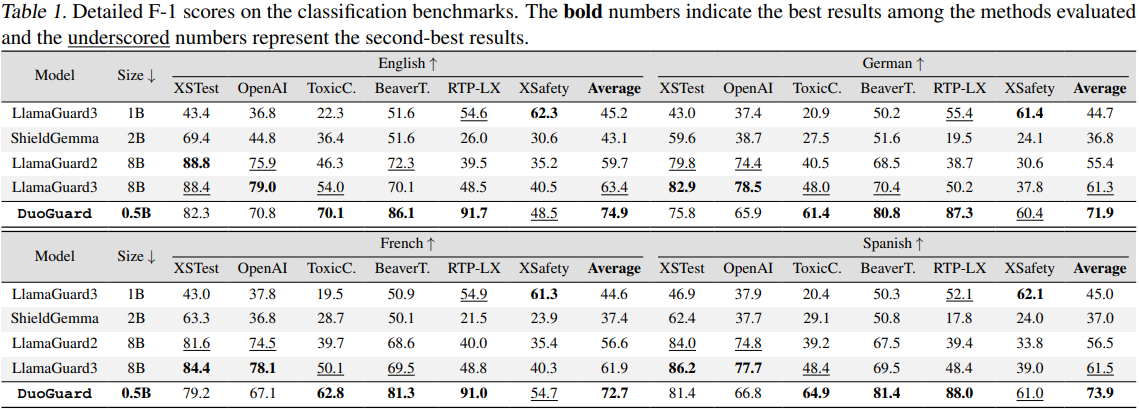
   • 생성자에 의한 LLM의 입력 또는 출력 사례 중 가드레일 모델이 오분류한 사례를 최소화
     → 훈련 시 현재 생성된 데이터 분포 $p_{\phi_t}(e_x|x,y)$에 대해 실제 레이블의 negative log-likelihood를 최소화하도록 함
     $\theta_{t+1} = \underset{\theta}{\operatorname{argmax}} \mathcal{L}_t^C(\theta), \quad \mathcal{L}_t^C(\theta) = \mathbb{E}_{e_x \sim p_{\phi_t}(e_x|x,y)} [-\log p_\theta(y|e_x)]$
   • 구현 시에는 binary cross-entropy loss를 사용한 다중 레이블 분류를 통해 12가지 유해 클래스에 대한 각 손실을 최소화하도록 함
     $\mathcal{L}_C^{(t)}(\theta) = - \frac{1}{|\mathcal{S}^{(t)}|}\sum_{(e_x,\{y_c\})\in\mathcal{S}^{(t)}} \sum_{c=1}^{12} [y_c \log p_\theta(y_c|e_x) + (1-y_c) \log(1-p_\theta(y_c|e_x))]$
2. 생성자
   • 생성자에 의한 LLM의 입력 또는 출력 사례 중 가드레일 모델이 오분류한 사례를 최대화
     • 훈련 시 오분류를 야기하는 샘플의 가능성을 높이도록 하는 DPO 적용
     • 리워드는 가드레일 모델의 실제 레이블에 대한 negative log-likelihood $r_t((x,y), e_x) = -\log p_{\theta_t}(y|e_x)$로 정의
       $\phi_{t+1} = \underset{\phi}{\operatorname{argmax}} \mathcal{L}_t^G(\phi, \phi_{\text{ref}}) \\ \mathcal{L}_G(\phi, \phi_{\text{ref}}) = \mathbb{E}_{e_x^w,e_x^l \sim p_{\phi_t}(e_x|x,y)} \left[ \beta \log \frac{p_\phi(e_x^w|x,y)}{p_{\phi_{\text{ref}}}(e_x^w|x,y)} - \beta \log \frac{p_\phi(e_x^l|x,y)}{p_{\phi_{\text{ref}}}(e_x^l|x,y)} \right]$
       여기서 $\phi_{\text{ref}}$는 레퍼런스 생성자 모델이고 $\beta$는 정규화 파라미터임

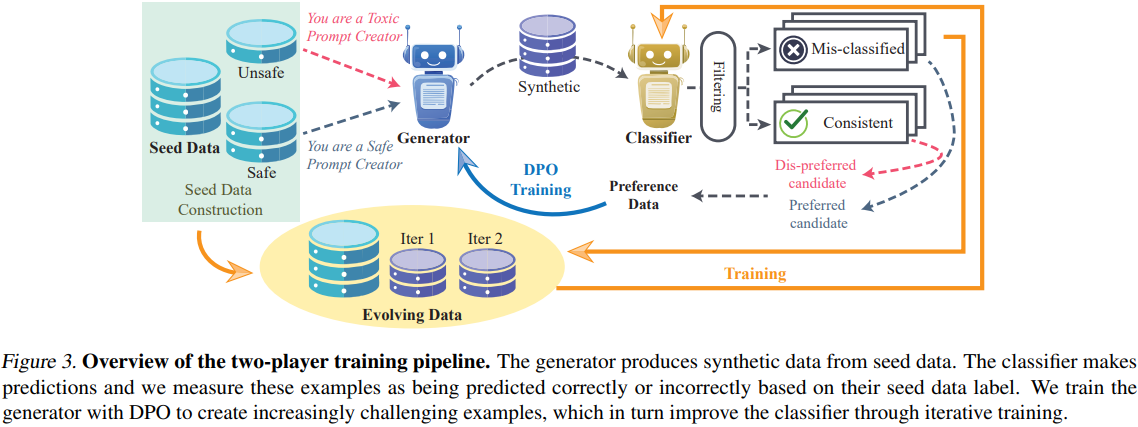
Experimental Result