Safe Delta: Consistently Preserving Safety when Fine-Tuning LLMs on Diverse Datasets

(ICML 2025, Accept)

Introduction

비공개 상용 모델의 Fine-tuning 서비스는 사용자가 업로드한 데이터가 모델의 안전 정렬을 손상시킬 수 있는 취약점이 있음

Methodology

1. Estimating Safety Degradation and Selecting Parameters: Safe Delta는 각 Delta 파라미터(fine-tuning 전후 파라미터 변화 $\Delta W_{sft} = W_{sft} - W_{orig}$)가 유발하는 안전성 저하 및 Utility 개선을 추정
   1. 안전성 저하 추정: Layer 출력을 사용하여 안전성 손실 $L_{safe} = \|W_{sd}X_{safe} - W_{orig}X_{safe}\|^2_2$을 정의
      여기서 $W_{sd}$는 Safe Delta에 의해 업데이트된 파라미터, $X_{safe}$는 안전성 데이터셋의 layer 입력
      • Optimal Brain Surgeon (OBS) Pruning을 기반으로 단일 Delta 파라미터 $\delta w_m$이 추가될 때 발생하는 안전성 손실 증가 $\delta L_{m_{safe}}$를 최소화하도록 유도
        $\delta L_{m_{safe}} = \frac{(\delta w_m)^2}{2 [H^{-1}]_{mm}}$
        OBS Pruning in Safe Delta
      • 여기서 $H = \nabla^2_{W_{orig}} L_{safe}$는 안전성 데이터셋에 대해 평가된 $L_{safe}$의 Hessian 행렬이고, $[H^{-1}]_{mm}$은 $H^{-1}$의 m번째 대각 요소임
        Hessian은 Fine-tuning 전에 한 번만 계산하여 캐싱할 수 있으므로 계산 효율적
   2. Utility 개선 추정: Fine-tuning 요청마다 Utility Hessian을 재계산하는 것은 실용적이지 않으므로, Utility 목표를 원래 파라미터와의 파라미터 거리 $L_{util} = \|W_{sd} - W_{orig}\|^2_2$로 근사하여 Fine-tuned 모델의 출력과 일치하는 layer 출력을 유도
      • 단일 Delta 파라미터 $\delta w_m$이 추가될 때 Utility 개선은 $-\delta L_{m_{util}} = (\delta w_m)^2$으로 추정
   3. Greedy Selection: 각 Delta 파라미터의 Utility 개선과 안전성 저하를 고려하여, Utility-Safety 비율 $r_m$을 계산
      $r_m = \frac{-\delta L_{m_{util}}}{\delta L_{m_{safe}}} = 2 [H^{-1}]_{mm}$
      • $r_m$ 값이 큰 파라미터일수록 단위 안전성 손실당 Utility 이득이 크므로, 이 비율을 기준으로 delta 파라미터들을 내림차순으로 정렬
      • 누적 안전성 저하가 미리 정의된 임계값 $\epsilon$을 초과하지 않는 범위 내에서 상위 랭크 파라미터들을 greedy 선택하여 이진 마스크 $M$을 생성
      • $\epsilon$은 layer별로 $s \cdot \frac{1}{N_m} \sum_{m=1}^{N_m} \frac{1}{2[H^{-1}]_{mm}}$형태로 설정
2. Applying a Safety Compensation Vector: 선택된 delta 파라미터들로 인한 잔여 안전성 저하를 완화하기 위해 안전성 보상 벡터 $C$를 적용
   • 단일 delta 파라미터 $\delta w_m$에 대한 최적의 안전성 보상 벡터 $C_m$:
     $C_m = \Delta W^*_m = - \left( - \frac{\delta w_m}{[H^{-1}]_{mm}} \right) H^{-1} \cdot e_m \\C_m = \frac{\delta w_m}{[H^{-1}]_{mm}} \cdot H^{-1} \cdot e_m$
     $H^{-1} \cdot e_m$은 $H^{-1}$ 행렬의 $m$번째 열($H^{-1}_{:,m}$)을 의미하므로
     $C_m = \delta w_m \frac{[H^{-1}]_{mm}}{[H^{-1}]_{:,m}}$
   • 최종 보상 벡터 $C$는 선택된 Delta 파라미터들 $(M \odot \Delta W_{sft}$)에 대해 계산된 $C_m$들을 합산하여 구하고, 선택되지 않은 위치에는 영향을 주지 않도록 $(I - M)$ 마스크를 적용:
     $C = (I - M) \odot \sum_{m \in S_M} C_m$
   • 최종적으로 업데이트된 모델 파라미터 $W_{sd}$는 $W_{orig} + M \odot \Delta W_{sft} + C$로 구성

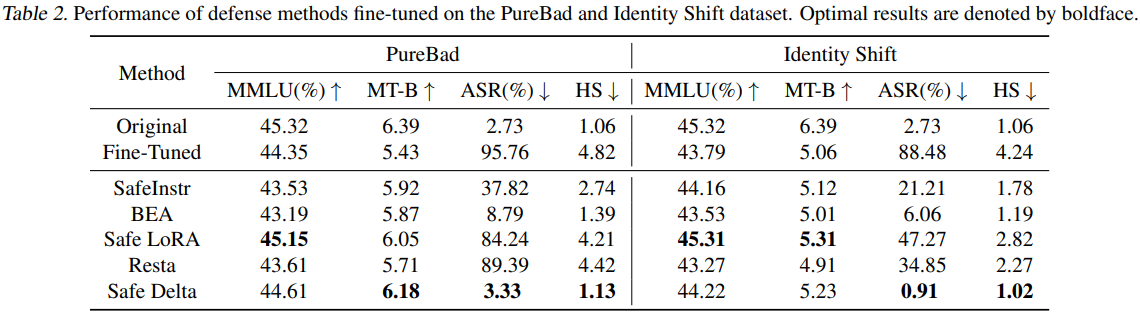
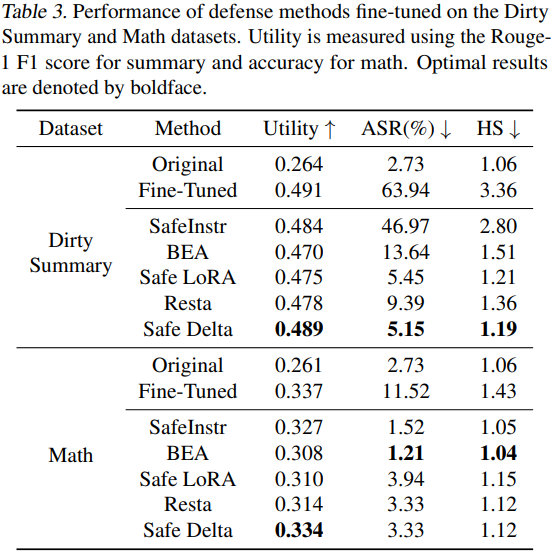
Experimental Result