Safety Alignment Should be Made More Than Just a Few Tokens Deep

(ICLR 2025, Accept Oral)

Introduction

기존의 안전 정렬은 '얕은 안전 정렬(shallow safety alignment)'이라는 공통된 문제, 즉 정렬이 모델의 생성 분포를 주로 처음 몇 개의 출력 토큰에만 적응시키는 문제가 있음

Methonology

1. 얕은 안전 정렬의 특징:

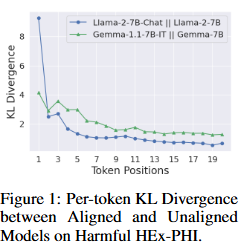
   정렬된 모델($\pi_{aligned}$)과 정렬되지 않은 모델($\pi_{base}$) 간의 토큰별 KL Divergence를 보면 초기 몇 개의 토큰에서 현저히 높게 나타남. 즉 $\pi_{base}$조차도 'I cannot'과 같은 거부 접두어를 강제로 채워 넣으면 유해성 비율이 크게 감소할 정도로 초기 접두어 토큰을 정렬하는 것은 Safety Shortcut이라 할 수 있음
   

2. 얕은 안전 정렬의 취약점:

   1. 추론 단계 취약점
      1. Prefilling Attacks: 얕은 안전 정렬된 모델의 후속 토큰 생성 분포는 정렬되지 않은 모델과 크게 다르지 않기 때문에, 유해한 답변의 첫 몇 토큰을 모델에 미리 제공하면 정렬된 모델도 유해한 콘텐츠를 생성할 가능성이 크게 증가
      2. Optimization Based Jailbreak Attacks (Adversarial Suffix Attacks): 'Sure, here is...'와 같은 긍정 접두어의 생성 확률을 최대화하는 대리 목표(surrogate objective)를 사용하여 초기 거부 토큰을 우회
      3. Jailbreak via Mere Random Sampling: 디코딩 매개변수(temperature, top-k, top-p)를 변경하여 무작위 샘플링을 통해 하면 초기 거부 토큰에서 벗어나 얕은 안전 정렬을 우회
   2. Fine-tuning 공격
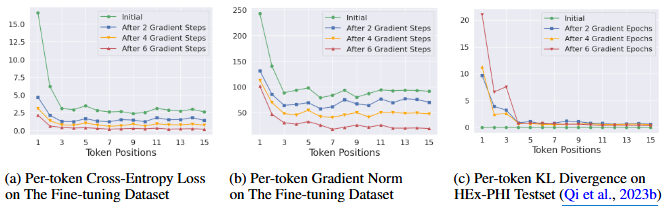
      유해한 Fine-tuning 데이터로 모델을 학습시키면, 초기 토큰 위치에서 cross-entropy loss가 현저히 높아지고 해당 gradient norm도 훨씬 커짐 → 수번의 반복만으로 ASR 급증
      
      

3. 얕은 안전 정렬의 개선:
   안전 정렬의 효과가 처음 몇 토큰 이상으로 깊어진다면 취약점에 대해 더 강력한 견고성을 가질 것

   1. Data Augmentation with Safety Recovery Examples:
      1. 유해한 지시 $x$, 그에 대한 유해한 응답 $h$, 그리고 거부 응답 $r$에서 $\pi_{\theta}(r|x, h_{\le k})$의 안전 정렬을 강화
         여기서 $k$는 유해한 접두어의 길이이며, $k=0$일 확률 50%, $k \sim Uniform[1, 100]$일 확률 50%인 Uniform 분포 $P_k$에서 샘플링됨
      2. 손실 함수 ($D_H$는 안전 데이터셋, $D_B$는 유틸리티 데이터셋이며, $\alpha=0.2$)
         $\min_{\theta} \alpha \times \left\{ \mathbb{E}{\substack{(x,h,r)\sim D_H, \\ k\sim\mathcal{P}k}} -\log \pi{\theta}(r|x, h{\leq k}) \right\} + (1 - \alpha) \times \left\{ \mathbb{E}{(x',y')\sim D_B} -\log \pi{\theta}(y'|x') \right\}$
      3. 상기 데이터 및 손실 함수에 의한 Fine-tuning은 유해한 쿼리의 중후반 토큰 생성에 대한 거부 답변의 KL Divergence를 높여 안전 정렬의 효과를 더 깊이 확장시키며, 모델 성능 저하를 억제

4. Fine-tuning 시 초기 토큰 보호:
   Fine-tuning 모델($\pi_\theta$)의 초기 토큰 logits 분포가 $\pi_{aligned}$를 크게 벗어나지 않도록 제약하는 손실 도출

   $\nabla \left( \frac{2}{\beta_t} S(\beta_t \Delta_t(\mathbf{x}, y_{<t}, y_t)) \right) = -2\sigma(\beta_t \Delta_t(\mathbf{x}, y_{<t}, y_t)) \nabla \log \pi_\theta(y_t | \mathbf{x}, y_{<t})$

   • $\sigma(z) := \frac{1}{1+e^{-z}}$는 sigmoid function이고, $S(z) := \log(1+e^z)$는 softplus function이며, $\beta_t$는 각 토큰 위치에서의 제약 강도를 조절하는 상수 매개변수
   • $\Delta_t(x, y{<t}, y_t):=\log \pi_{\text{aligned}}(y_t | x, y_{<t}) - \log \pi_{\theta}(y_t | x, y_{<t})$
   • 만약 $\Delta_t$가 크고 양수($\pi_{aligned}$이 더 높음): $\sigma(\beta_t\Delta_t)\approx1 → w_t\approx2$ (강하게 $-\nabla\log\pi_\theta$를 적용하여 $\pi_\theta$를 $\pi_{aligned}$ 쪽으로 끌어당김)
   • 만약 $\Delta_t$가 음수($\pi_\theta$이 이미 $\pi_{aligned}$보다 높음): $\sigma(\beta_t\Delta_t)\approx0$ → 기여 거의 없음 (더 이상 밀어붙이지 않음)
   • $\beta_t$가 작아 $\beta_t\Delta_t$가 작으면 $\sigma(\beta_t\Delta_t)\approx 1/2$ 이므로 $w_t\approx1$. 결과적으로 기울기가 일반 cross-entropy와 거의 동일해짐

   $\beta_t$는 초기 토큰($t$가 작을 때)에 더 큰 값을 부여하여, 해당 토큰 위치에서 $\pi_{\theta}$의 생성 분포가 $\pi_{\text{aligned}}$로부터 크게 벗어나지 않도록 제약
   반대로, 후반부 토큰($t$가 클 때)에는 더 작은 $\beta_t$ 값을 적용하여 모델이 주어진 미세 조정 데이터에 더 자유롭게 적응할 수 있도록 함
   

Experimental Result