최소신장트리

신장 트리 : 그래프의 모든 정점과 간선의 부분 집합으로 구성되는 트리
간선의 갯수는 노드 갯수 - 1 이 된다.

최소 신장 트리

• 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 트리
• 무 방향 가중치 그래프
• N개의 정점을 가지는 그래프에 대해서 반드시 (N - 1)개의 간선을 사용
• 사이클을 포함하지 않는다. (사이클이 사용되면, 트리의 조건도 벗어나게 된다)

• 도로망, 통신망, 유통망 등등 여러 분야에서 비용을 최소로 하여 이익을 볼 수 있는 것
• 크루스칼, 프림 알고리즘 등 ...

크루스칼 알고리즘

1. 최초, 모든 간선을 가중치에 따라 간선을 오름차순으로 정렬한다.
2. 가중치가 가장 낮은 간선부터 선택하면서, 트리를 증가 시킨다.
   → 사이클이 존재하면 다음으로 가중치가 낮은 간선을 선택 (find 연산으로 찾는다)
3. N-1개의 간선이 선택될 때까지 2번을 반복한다.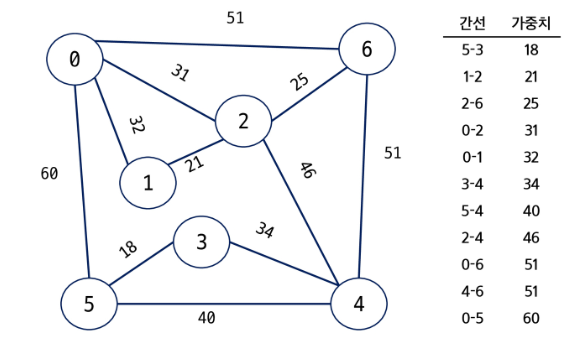

• 그리디 알고리즘 (가장 적합하다고 생각되는 것을 반복적으로 증명하는 것)의 일부

• 예시
  

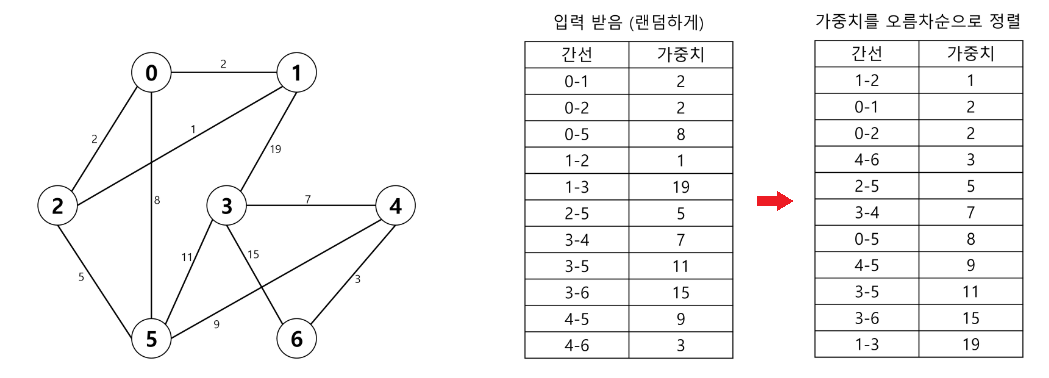
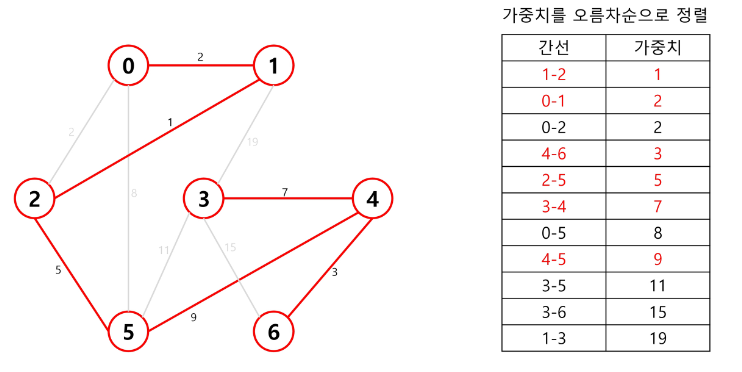
• union 이라고 생각을 하면 된다.

새로운 문제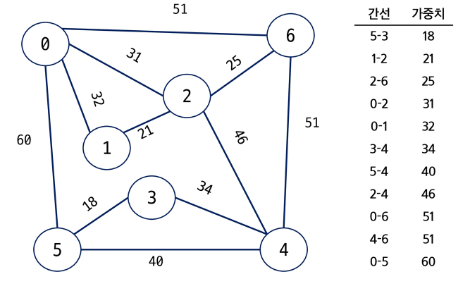

import java.util.Arrays;
import java.util.Comparator;
import java.util.Scanner;

public class 크루스칼 {
	static class Edge   {
		int A, B, W;
		
		public Edge(int a, int b, int w) {
			this.A = a;
			this.B = b;
			this.W = w;
		}

//		implements Comparable<Edge> 를 사용하는 경우 
//		@Override
//		public int compareTo(크루스칼.Edge o) {
//			return this.W - o.W;
//		}
	}
	
	static int[] p; // 대표자를 저장할 배열 
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(input);
		
		int V = sc.nextInt(); // 정점의 개수
		int E = sc.nextInt(); // 간선의 개수 
		
		Edge[] edges = new Edge[E];
		int[][] edge = new int[E][3]; // 2차원 배열로 생성하여 작성해도 된다. 
		
		for(int i = 0; i <E ; i++ ) {
			int A = sc.nextInt();
			int B = sc.nextInt();
			int W = sc.nextInt();
			
			edges[i] = new Edge(A, B, W);
		}
		
		
		// 크루스칼 1 : 가중치 순으로 정렬 
		// 만든 class 에서 정렬을 하거나, comparator를 작성해 주면 된다. 
		Arrays.sort(edges, new Comparator<Edge>() {

			@Override
			public int compare(크루스칼.Edge o1, 크루스칼.Edge o2) {
				return o1.W - o2.W;
			}
		});
		
		
		// 크루스칼 2 : V-1개의 간선을 뽑는 것이 필요 
		// 단, 사이클 생성되지 않게. union find 사용 
		p = new int[V]; // 입력 값이 0번부터 시작하기 때문에, v개로 만들면 된다. 
		
		// make-set을 통해서, 전체 자신을 대표로 만드는 작업 
		for(int i = 0; i < V ; i++) {
			p[i] = i;
		}
		
		int result = 0;		// 최소 비용을 저장 
		int pick = 0; 		// 뽑은 간선의 개수를 출력 
		
		for(int i = 0; i < E; i++) {
			int x = edges[i].A;
			int y = edges[i].B; 
			
			
			// 사이클 발생 여부 검사
			// 해당 블록에 들어가면 사이클이 아니라는 뜻이다. 
			if (findSet(x) != findSet(y)) {
				union(x,y);
				result += edges[i].W;
				pick++;
			}
			
			if (pick == (V-1)) break; // 크루스칼 3 : 간선의 총 개수가 돌면서 뽑은 수량이라면 종료
		}
		
		System.out.println(result);
		
		
	}
	
	static int findSet(int x) {
		if(p[x] != x) p[x] = findSet(p[x]);
		return p[x];
	}
	
	static void union(int x, int y) {
		// x와 y가 대표자여야 한다. 
		// rank를 고려하지 않기 때문에 상호배타집합을 넣어주기만 하면 된다. 
		p[findSet(y)] = findSet(x);
	}