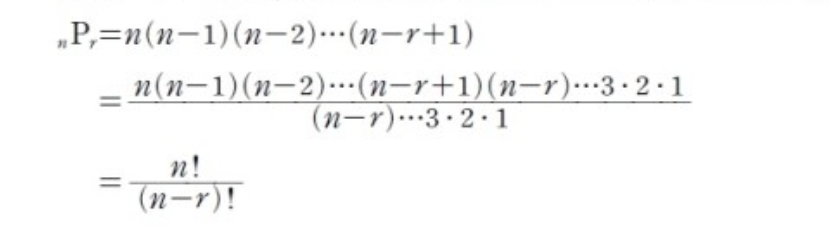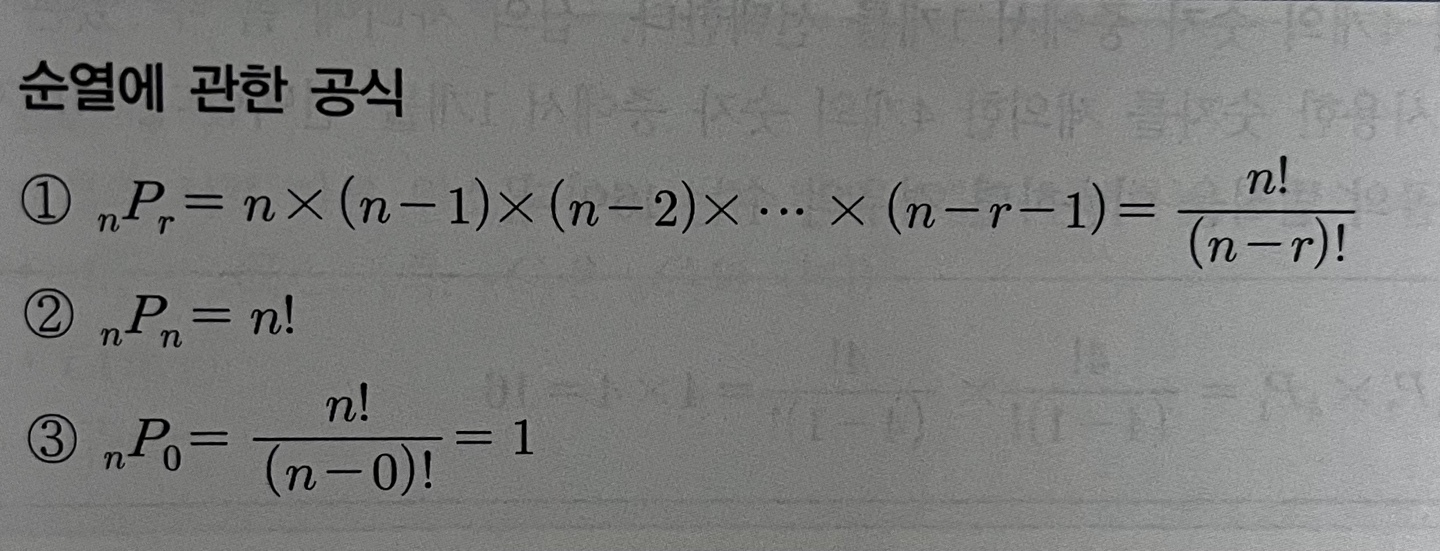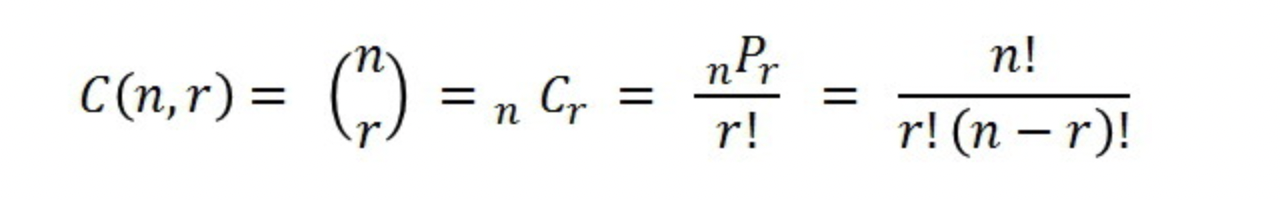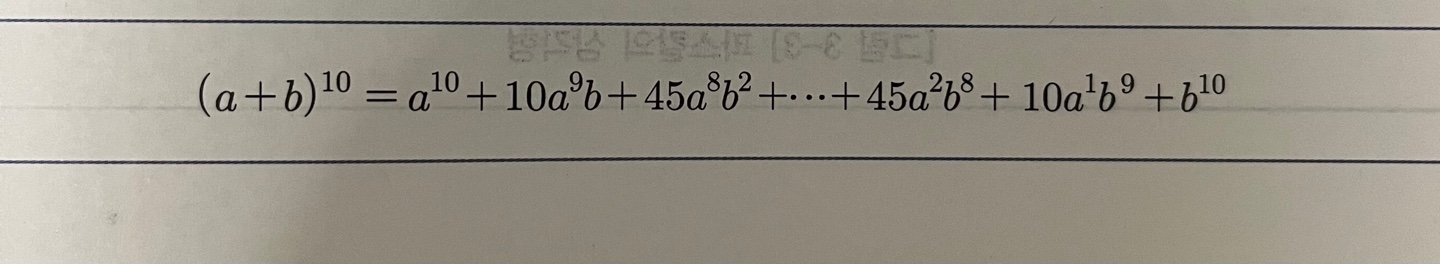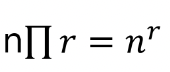이산수학 : 순열과 조합

김지원·2023년 4월 17일

목록 보기

6/11

사건 : 어떤 실험이나 관찰에서 주어진 조건을 만족하는 집합
경우의 수 : 사건의 발생 건수. 트리나 표를 이용해 구한다.

ex) 주사위를 던져서 홀수가 나오는 경우 집합 표현
사건 : {1,3,5}
경우의 수 : 3

계수의 법칙

❗️ 어떤 사건이 발생할 경우의 수를 구할 때 일정한 기준을 정하고 그 기준에 의하여 누락되지 않고 중복되지 않게 구해야한다.

여러 사건에 대한 기본적인 계수의 법칙 2가지

합의 법칙

rule of sum

: 합의 법칙의 기본은 전체 작업의 수를 구할 떄 각 작업의 수를 더하여 계산한다.
1) 두 사건이 서로 독립일 때 (A ∩ B = ∅)
각각의 경우의 수가 |A| = m, |B| = n 이라면
사건 A 또는 사건 B가 일어날 경우의 수 : m + n
2) 두 사건이 서로 독립이 아닐 때 (A ∩ B ≠ ∅, 교집합 존재할 때)
동시에 일어나는 경우의 수 l
사건 A 또는 사건 B가 일어날 경우의 수 : m + n - l
예시)
ex) 한 개의 주사위를 던져서 짝수 또는 소수의 눈이 나올 경우의 수
짝수 {2,4,6} / 소수 {2,3,5} 3개씩 존재하고 
짝수이면서 소수 즉 교집합이 생기는 부분은 {2} 1개가 존재한다. 
따라서 3+3-1임으로 경우의 수는 5가 된다.

곱의 법칙

rule of poroduct

: 여러 개의 독립적인 작업들로 하나의 과정을 구성할 때 사용한다.

각각의 경우의 수가 |A| = m, |B| = n 이라면
사건 A와 사건 B가 동시에 일어날 경우의 수 : m * n

예시)

ex) 서울에서 대전을 들렀다가 부산으로 가는 방법
서울 → 대전 : 2(버스, 기차)
대전 → 부산 : 2(버스, 기차)
2 * 2 임으로 경우의 수는 4가 된다.

1에서 5까지 숫자를 이용해 3자리 난수를 생성할 때 경우의 수
각 자리를 A,B,C라고 할 때 |A|,|B|,|C| = 5가 된다. 
곱의 법칙을 이용해 5 * 5 * 5 = 125가지가 나오게 된다.

순열과 조합

일반적으로 어떤 사건이 발생하는 경우의 수를 셀 때 순열과 조합을 사용한다.

사건의 순서에 의미를 두는 경우 : 순열

사건의 순서에 의미를 두지 않는 경우 : 조합

사건들을 모아놓은 어떤 집합에서 일정 계수를 선택할 때

선택만 할 때 : 조합문제

순서도 고려 할 때 : 순열문제

중복 허용 여부에 따라서 또 나눠지게 된다.

중복을 허용하지 않는 순열과 조합

순열

Permutation

: 서로 다른 원소들을 순서를 고려하여 일렬로 배열하는 것

서로 다른 n개의 원소를 한 줄로 배열하는 순열의 개수 n부터 1까지 하나씩 감소한 수를 곱하여 구할 수 있다.
이것을 n팩토리얼(factorial) 또는 n의 계승이라고 한다.
n! = n X (n-1) X (n-2) X ... X 2 X 1
<팩토리얼의 일반적인 규칙>
0! = 1 / 1! = 1 
예시)
30명 학급에서 반장, 부반장, 총무를 각 1명씩 선출하는 경우
30명 중 반장 1명을 뽑으면 부반장은 29명 중에서 1명을 뽑게 되고 총무는 28명 중에서 1명을 뽑게 된다. 
이와 같이 서로 다른 n개의 원소 중 특별히 r개만을 선택하여 순서대로 나열하는 경우가 발생하는데 이러한 경우를 r-순열 이라고 한다.
r-순열의 개수는 r-순열수 라고 하며 P(n,r) 또는 nPr 로 표기한다.
수식 : n X (n-1) X (n-2) X ... X (n-r+1)
r-순열수를 팩토리얼을 이용해 나타내면 다음과 같다.

조합

Combination

: 순서가 없는 순열
조합의 수 = 선택된 원소에 대한 순열의 수 / 동일하게 여겨지는 나열의 수
n개의 서로 다른 원소들 중에서 r개의 원소를 순서를 고려하지 않고 추출하는 것을 r-조합이라고 한다.
예시1)
{x,y,z}의 조합
=> ∅, {x}, {y}, {z}, {x,y}, {y,z}, {x,z}, {x,y,z} 
이 중에서 2-조합을 뽑으면 {x,y}, {y,z}, {x,z} 이다.

임의의 집합 A에서 r개의 원소로 이루어진 부분집합 : A의 r-부분집합
이러한 집합의 조합은 곧 그 집합의 부분집합이므로 r-조합은 r-부분집합이라 할 수 있다.
<r-조합의수>

조합은 5개에서 2개를 선택하는 거나 5개에서 3개를 선택하는 것은 같은 의미임으로 5C3 = 5C2 가 된다. 따라서 nCr = nCn-r 이 성립한다.

조합 기호 표현 : C(n,r) C n,r
예시2)
위와 같이 차수가 큰 이항식이 조합으로 해석을 하게 되면
a와 b 두 개의 문자 10개를 선택해서 나열하는 조합이 된다.
첫 번째 항 a10은 문자 a만 10개 선택해 나열한 것으로 경우의 수는 10C10 = 1 이 된다.
두 번째 항 : 10C9 = 10C1 = 10
이 조합의 경우의 수는 각 항의 계수가 된다.
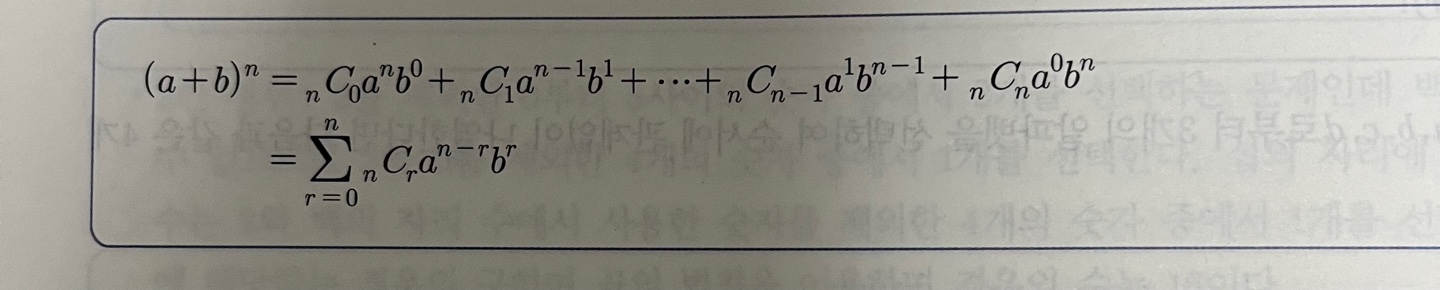
(a+b)^n 을 전개하게 되면 이와 같은 식이 된다.
이와 같은 식의 전개를 이항 정리(binomial theorem) 이라고 하고
이때 nCr 을 이항 계수(binomial coefficient) 라고 한다.

이항 계수와 관련하여 중요한 항등식으로 파스칼의 삼각형(pascal's triangle)이 있다.
파스칼의 항등식 (= 파스칼의 삼각형)
n>=2, 1<=r<=n 인 모든 양의 정수 n,r에 대해 다음이 성립한다. 
nCr = n-1Cr-1 + n-1Cr

중복을 허용하는 순열과 조합

중복 순열 (일반 순열)

permutation with repetition

: 서로 다른 n개의 원소 중 r개를 중복 허용하며 선택하여 순서대로 나열한 것.
"모든 원소들이 서로 다르다" 는 조건에서 같은 원소의 중복을 허용하는 순열이다.

예시)
네 개의 숫자 1,2,3,4 중에서 세 개의 숫자를 나열하여 세 자리의 숫자를 만드는 경우
'서로 다른' 이라는 전제 없이 세 개의 숫자를 나열하므로 
백의 자리, 십의 자리, 일의 자리 모두 같은 숫자가 올 수 있다.
4 X 4 X 4 =  64 가지가 된다.

같은 원소를 반복하여 쓰는 집합을 다중집합(multiset) 이라고 한다.
예시)
주머니에 흰색 바둑돌 5개 검은색 바둑돌이 4개가 있을 때 
흰색돌 = a / 검은색돌 = b 라고 하면 
다중집합 {5 x a, 4 x b} 로 표현할 수 있다.
❗️ => 반복하는 원소가 있는 순열 : 곱의 법칙 이용