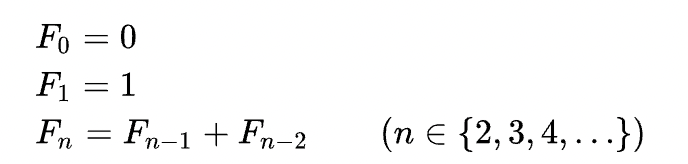수열 : 어떤 규칙에 따라서 원소들을 나열해 놓은 것

점화식

recurrence relation

: 어떤 수열의 각각의 항들의 관계를 나타낸 식, 재귀적 관계
점화식의 해 : 점화식을 만족하는 수열
점화식의 해를 찾는 것 = "점화식을 푼다" 라고 한다.
예시)

1부터 시작하여 앞의 항에 3을 곱하여
다음 항을 만드는 수열 1,3,9,27,...이 있을 때 n번째 항의 표현
=> xn = xn-1 X 3

즉, 점화식은 이전의 항(xn-1, xn-2)에 의하여 n번째 항 xn을 표현하는 식이라 할 수 있다.

• 초기조건(=점화식은 처음 항 몇 개)이 적절하게 주어지면 수열의 모든 항을 구할 수 있다.

재귀적 정의 (recursive definition)

수학적 귀납법에서와 같이 첫 번째 항이 정의되고 n+1번째 항은 바로 앞의 항인 n번째와 그 이전의 항들과의 관계로써 정의될 경우.

• 점화식으로 표현한다.

점화식을 이용한 문제 해결

단계1) 주어진 문제를 원래의 문제와 같은 형태의 더 작은 문제들로 분할한다.
단계2) 가장 작은 문제로 불할된 문제들의 해를 구한 후, 최종적으로 이 해들을 결합해 주어진 문제의 해를 구한다.

점화식에 의해 나타나는 현상 Ex

프랙탈(Fractals) : 일부 작은 조각이 전체와 비슷한 기하학적 형태

점화식 대표적인 예

피보나치수

Fibonacci numbers

: 첫째, 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열.

1,1,2,3,5,8,13....

피보나치수 점화식 ↓

하노이 탑

Tower of Honoi

: 퍼즐의 한 종류이며 서로 다른 크기의 원반들이 판 위에 세워진 세 개의 막대로 구성되어있다.
다음 조건을 만족 시키면서 한 막대에 꽂힌 원판들을 그 순서 그대로 다른 막대로 옮겨서 쌓는 것이다.

1. 한 번에 한개의 원판만 옮길 수 있다.
2. 가장 위에 있는 원판만 이동할 수 있다.
3. 큰 원판이 작은 원판 위에 있어서는 안 된다.

원판이 n개 일 때 2^n-1번 의 이동으로 원판을 모두 옮길 수 있다.

점화식의 해

반복법

Iteration method

: 앞의 항을 반복적으로 나타내 해를 구하는 방법.
예시)

점화식이 an = 2an-1, a0 = 1, 일 때 반복법을 이용해 해를 구해보자
an = 2 X an-1 = 2 X (2 X an-2) = 2^2an-2 = ... = 2^na0 = 2^n

상수계수의 선형동차점화식

: 점화식의 계수가 모두 상수인 선형 점화식.
점화식을 구하는 방법으로 상수계수의 선형동차점화식을 이용해 특성방정식을 구하고 이를 이용해 점화식의 근을 구한다.
상수계수의 선형동차점화식 공식
음이 아닌 정수 = k
cn, cn-1, ... cn-k = 실수인 상수
cn != 0, cn-k != 0 이고 an은 n의 함수라고 가정할 때, 차수가 k인 상수계수의 선형점화식은 다음과 같다.