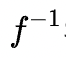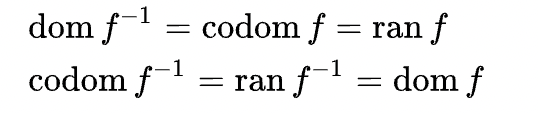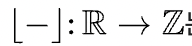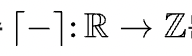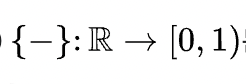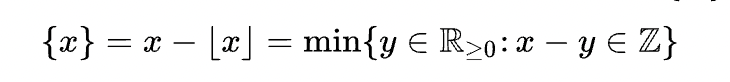반 순서
: 반 순서 관계(partial order relation, 부분 순서 관계)
집합 A에 대한 관계 R이 반사 관계, 반 대칭 관계, 추이 관계 성립되어야함.
- 반 순서 관계가 성립되면 순서가 있다는게 확실해진다.
반 순서 집합
partially ordered set
: 반 순서를 갖춘 집합
cf) 반순서(부분 순서) : 순서 및 나열 등의 개념을 추상화한 이항 관계
- 전순서 집합과 달리 모든 원소가 비교 가능할 필요는 없다.
- 원순서 집합과 달리 순서가 같은 여러 원소는 존재하지 않아야한다.
전순서(선형 순서) 집합 : 임의의 원소끼리 순서가 주어진 경우 원순서 : 반사 관계, 추이 관계만 성립하는 경우
선형 순서 집합
linearly ordered set
: 집합 A의 모든 두 원소가 비교 가능하면 A를 선형 순서 집합이라고 함.
완전 순서 집합
total order set
: 완전 순서인 관계가 있는 집합 A
- 완전 순서 : 집합 A에서의 관계 R이 반 순서 관계이고 집합 A모든 원소들을 그 관계에서 비교할 수 있는 관계 R
- 비교 불가능한 관계가 하나라도 있으면 성립될 수 없음.
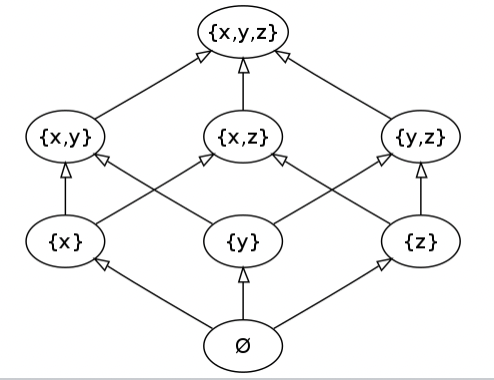
하세 도형 (하세 도표)
: 반 순서 집합을 그래프로 나타냄
방향 그래프의 한 종류이지만 화살표 없이 모든 연결선을 트리와 같이 위에서 아래로 향하게 그린다.1) 모든 순환은 표시하지 않음(반사 관계 성립하기 때문에 생략함) 2) 반 대칭 관계가 성립하기 때문에 비교하여 우선적으로 오는 원소를 아래쪽에 그림. 3) 집합 A의 원소 x,y,z에서 x<=y이고 y<=z를 만족하는 y가 존재하지 않을 경우에만 x에서 y로의 연결을 그림.
반 순서 관계에서 원소 간 비교가 가능할 때, 그 원소의 위치를 판별하는 방법
극대원소
: 반 순서 집합 A의 원소 a에 대해 a<b인 원소 b가 집합 A에 존재하지 않는 경우의 원소 a
즉, a다음에 오는 원소가 없다는 것이다.
- 하세도표로 나타내었을 때 가장 상위에 위치하는 하나 이상의 원소들(여러개 존재 가능)
- 극대 원소들 간의 우선순위는 동일함.
극대원소
: 반 순서 집합 A의 원소 a에 대해 b<a인 원소 b가 집합 A에 존재하지 않는 경우의 원소 a
즉, a보다 선행하는 원소가 없다는 것이다.
- 하세도표로 나타내었을 때 가장 하위에 위치하는 하나 이상의 원소들(여러개 존재 가능)
- 극소 원소들 간의 우선순위는 동일함.
최대원소
: 반 순서 집합 A의 모든 원소 a에 대해 a<=b인 A의 원소 a,
- 하세도표로 나타내었을 때 가장 상위에 위치하는 단 하나의 원소
- 집합에 속하는 원소들 중 우선순위가 가장 높은 원소 = 최대원소보다 우선 순위가 높거나 같은 원소는 존재하지 않는다.
최소원소
: 반 순서 집합 A의 모든 원소 a에 대해 b<=a인 A의 원소 b,
- 하세도표로 나타내었을 때 가장 하위에 위치하는 단 하나의 원소
- 집합에 속하는 원소들 중 우선순위가 가장 낮은 원소 = 최대원소보다 우선 순위가 낮거나 같은 원소는 존재하지 않는다.
동치 관계
equivalencerelation
: 관계 R에서 반사 관계, 대칭 관계, 추이 관계가 모두 성립하는 관계
집합의 원소들이 '같다'라는 것을 의미함.동치 관계 R에서 순서쌍 원소(a,b)에 대해 a와 b가 같다 라고 할 수 있다.
동치류 / 동치 클래스
equivalence calsses
: 이러한 같은 의미를 갖는 원소들을 모아놓은 집합
[x] = {y|(x,y) ∈ R} ([x] 는 그 원소와 동치인 원소들의 집합)
몫집합
quotient set
: 집합 A의 동치류의 모임
표현 : A/R = {[x] | x ∈ A}
- 집합 A의 동치관계 R에 대해 몫집합(A/R)은 A의 분할(partition)이다.
분할 : x,y ∈ A 에 대해 xRy 이면 [x] = [y] 이다. (x,y) ∉ R (R의 원소가 아니면) [x] ∩ [y] = ∅ 이다.
- 집합과 분할 사이에는 자연적인 일대일 대응이 존재함.
분할
공집합이 아닌 집합 A의 분할은 다음 조건을 만족시키는 A의 부분 집합의 모임을 의미함.
1) 집합 A의 모든 분할 집합은 공집합이 아님.
2) A안에 있는 모든 원소는 임의의 Ai에 속함
3) {Ai}의 집합의 서로 교차하지 않는다. (공통되는 데이터가 없어야함){1,2,3,4} {1,29}, {3,4} 이런식으로만 분할이 가능 한 것.
mod 합동
congruence
: x와 y를 m으로 각각 나누었을 때 나머지가 같은 것. 동치 관계이다.
x = y(mod m)
- 반사 관계 성립 : A = A(mod C)
- 대칭 관계 성립 : A = B(mod C) 이면 B = A(mod C) 이다.
- 추이 관계 성립 : A = B(mod C) 이고 B = D(mod C) 이면 A = D(mod C) 이다.
함수 : function
: 관계의 특수한 형태, 첫 번째 원소가 모두 다른 순서쌍들의 집합
A 집합에 있는 모든 x에 대하여 유일한 y가 존재한다면 u에서의 관계는 함수 관계라고 한다.
- 집합 A의 모든 원소가 반드시 집합 B의 원소 하나와 대응해야한다.
- 두 집합 A와 B에서 함수 f는 집합 A에서 B로의 관계의 뿐 집합
- 정의역의 각 원소를 정확히 하나의 공변역 원소에 대응시킨다.
f : A → B A : f의 정의역(domain) B : f의 공변역(codomain) f : 사상(mapping) ex) 함수 f는 A에서 B로 사상한다f : X → Y는 f(x) = y로 표현 가능 y => 함수 f에 의한 x의 상(image) 또는 함수값 x => 원상(preimage) y의 집합 : 치역(range) => 공변역의 부분집합, 공변역보다 작을 수 있음공함수(empty function) : 원소가 하나도 없는 빈 집합
공집합 ∅에 대해 임의 Y가 f : ∅ → Y 만족하는 함수. 공변역이 공집합이 됨.같다(equal) : 두 함수 f와 g에 대해 정의역 = 공변역, 모든 원소 x가 f(x) = g(x) 이면 함수 f와 g는 같다 라고 함.
함수 그래프
function graph
f : A → B에 대해 x ∈ A 이고 y = f(x) 인 순서쌍 (x,y)의 집합을 나타내는 그래프
G = {(x,y)|x ∈ A, y ∈ B, y = f(x)}그래프의 기하학적 표현 : 그래프 G 원소들을 좌표 평면상에 점으로 표시하는 것.
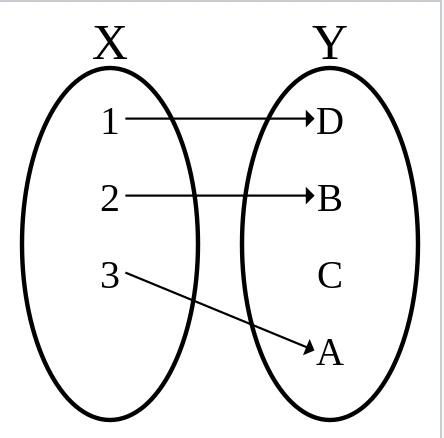
단사함수
injection function
: 정의역의 서로 다른 원소를 공변역의 서로 다른 원소로 대응시키는 함수, 일대일 함수(one-to-one function) 이라고 함.
- 단사함수의 치역은 공변역의 부분 집합이 된다.
∀aiaj ∈ A, f(ai) = f(aj) => ai = aj f : A → B ran(f) ⊆ B
- 집합 A와 B의 원소 개수 비교 :
|A| <= |B||dom(f)| <= |codom(f)| |ran(f)| <= |codom(f)| 정의역 원소 개수 <= 공변역 원소 개수 치역 원소 개수 = 공변역 원소 개수
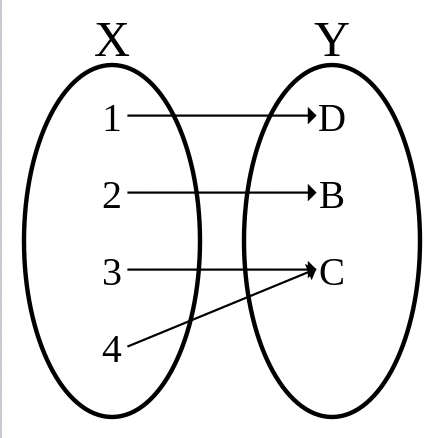
전사함수
surjective function
: 공변역과 치역이 같은 함수, 위로의 함수라고도함.
∀b ∈ B, ∃a ∈ A, f(a) = b f : A → B ran(f) = B
- 모든 함수의 관계가 집합 B의 모든 원소에 반영됨으로 반영 함수(onto function)라고도 한다.
|dom(f)| >= |codom(f)| |ran(f)| <= |codom(f)| 정의역 원소 개수 >= 공변역 원소 개수 치역 원소 개수 = 공변역 원소 개수
전단사함수
bijective function
: 단사함수를 만족하며 전사함수를 만족하는 함수, 일대일 대응 함수라고도 함.
|dom(f)| = |codom(f)| |ran(f)| = |codom(f)| 정의역 원소 개수 = 공변역 원소 개수 치역 원소 개수 = 공변역 원소 개수
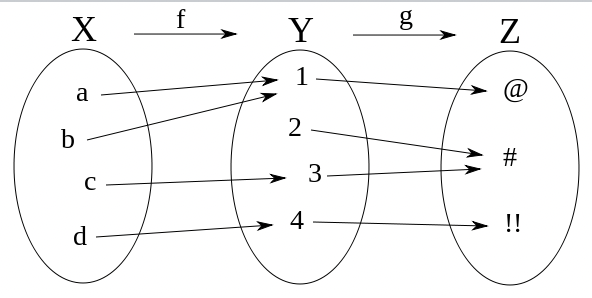
합성함수
composition function
: 한 함수의 공역이 다른 함수의 정의역과 일치하는 경우, 두 함수를 이어 하나의 함수로 만드는 연산
g ∘ f = {(a,c)|a ∈ A, b ∈ B, c ∈ C, f(a)=b, g(b)=c}
- f함수의 공변역 B와 g함수의 정의역 B가 같아야한다.
1) 함수 f, g가 단사, 전사, 전단사 → g ∘ f 단사, 전사, 전단사함수이다. 2) g ∘ f 가 단사함수 → f는 단사함수이다. 3) g ∘ f 가 전사함수 → g는 전사함수이다. 4) g ∘ f 가 전단사함수 → f는 단사함수이고 g는 전사함수이다.
항등함수
identify function
: 정의역과 공변역이 같은 집합이며 공변역과 치역도 같아야한다.
즉, 항등함수는 전단사 함수이다.어떤 함수 f의 항등함수의 합성 f : A → B이고 집합 A에 대한 항등함수가 IA, 집합 B에 대한 항등함수가 IB 일 떄 합성함수 f ∘ IA= IB ∘ f = f
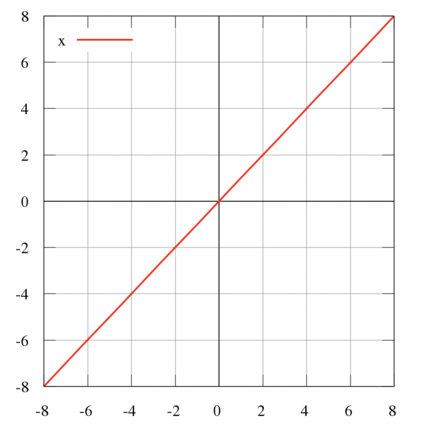
실수 항등 함수의 그래프
- 행렬로 표현하면 대각행렬이 1이고 나머지는 0인 모양을 가진다.
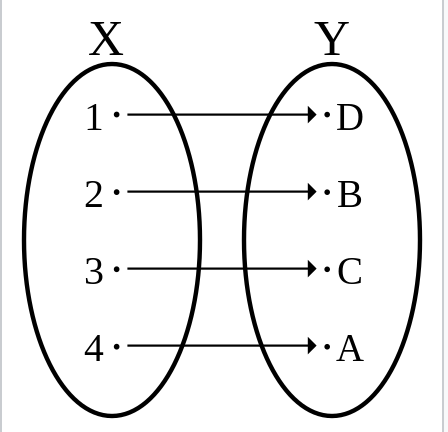
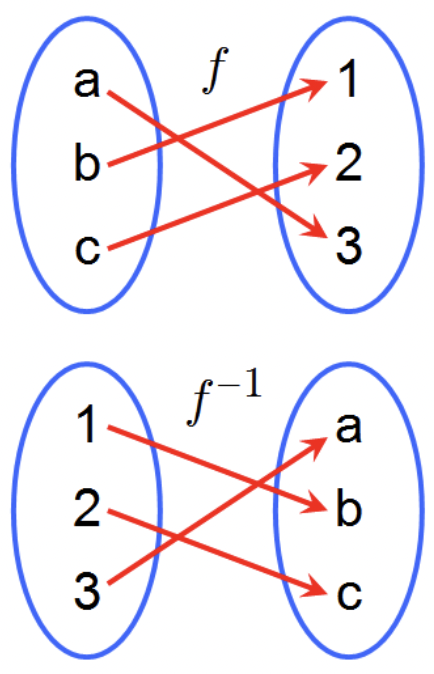
역함수
inverse function
: 정의역과 치역(함숫값)을 서로 뒤바꾸어 얻는 함수
역함수는 전단사함수의 경우에만 구할 수 있고 전단사함수는 가역함수가 된다.
즉, 역함수를 가질 필요 충분 조건은 전단사함수이다.
cf) 가역함수(invertible function) : 역이 존재하는 함수임의의 b ∈ B에 대해, b = f(a) 인 a ∈ A 가 유일하게 존재함
상수함수
constant function
: 정의역의 값에 관계없이 항상 같은 값을 갖는 함수
f(x) = 3
특성함수
characteristic function
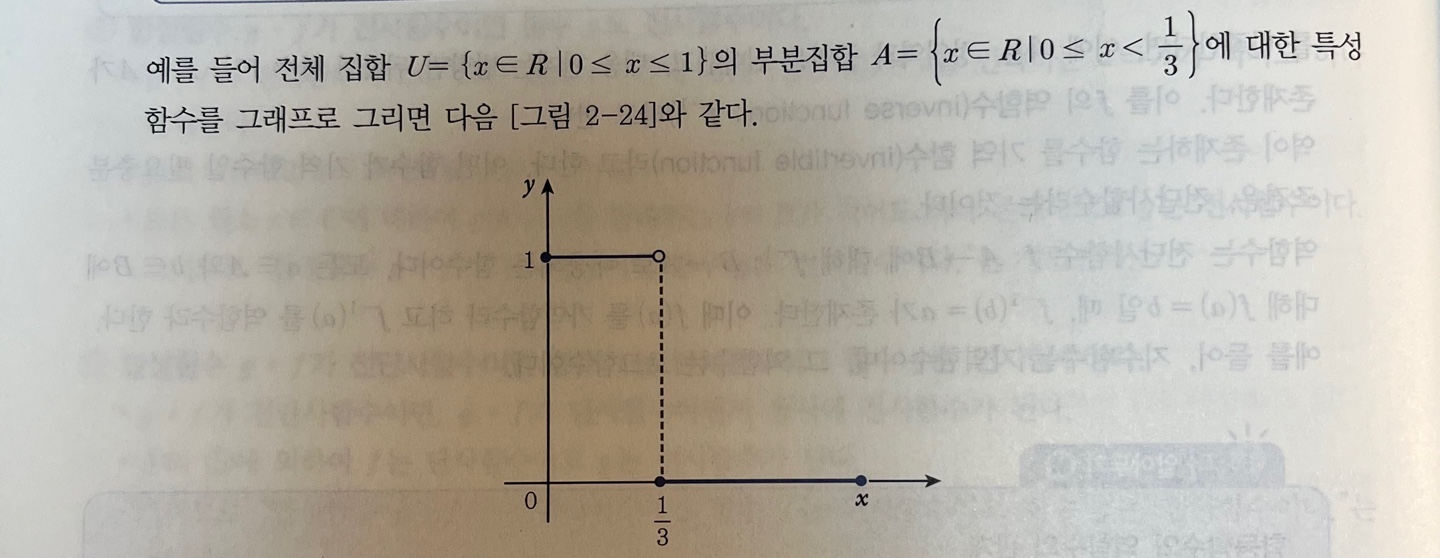
: 어떤 조건에 의해 만들어진 전체집합에 한 부분집합
전체 집합을 U라고 할 때 U의 부분집합 A의 특성함수 fa : U → {0,1}은 다음과 같이 정의된다.fa(x) = {0, x ∉ A // A집합의 원소가 아니면 A ⊂ U 1, x ∈ A'
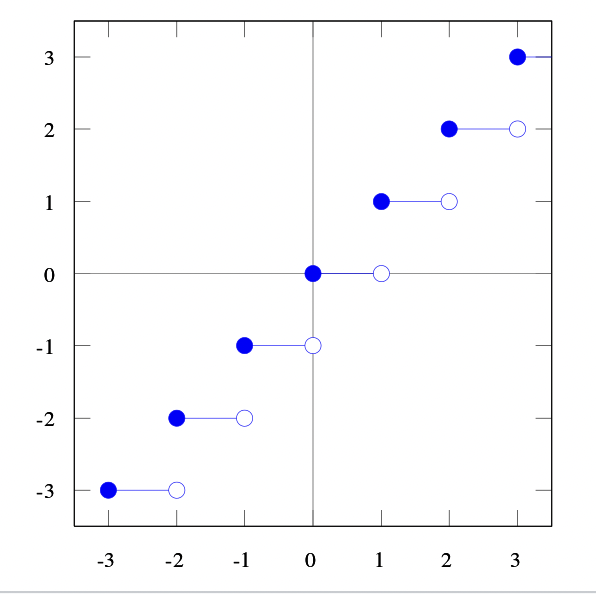
바닥함수(최대 정수 함수)
floor function
: 각 실수 이하의 최대 정수를 구하는 함수
내림함수, 버림함수라고도 한다.
R : 실수, Z : 정수 [x] = max{n ∈ Z : n <= x} 실수 x의 바닥 함수 값 : x와 같거나 그보다 작은 정수 가운데 가장 큰 하나의 정수 ex) [5.2] = 5, [-5.2] = -6
천정함수(최소 정수 함수)
ceiling function
: 각 실수 이하의 최소 정수를 구하는 함수
올림함수라고도 한다.
R : 실수, Z : 정수 [x] = min{n ∈ Z : n >= x} 실수 x의 바닥 함수 값 : x와 같거나 그보다 작은 정수 가운데 가장 작은 하나의 정수 ex) [5.2] = 6, [-5.2] = -5
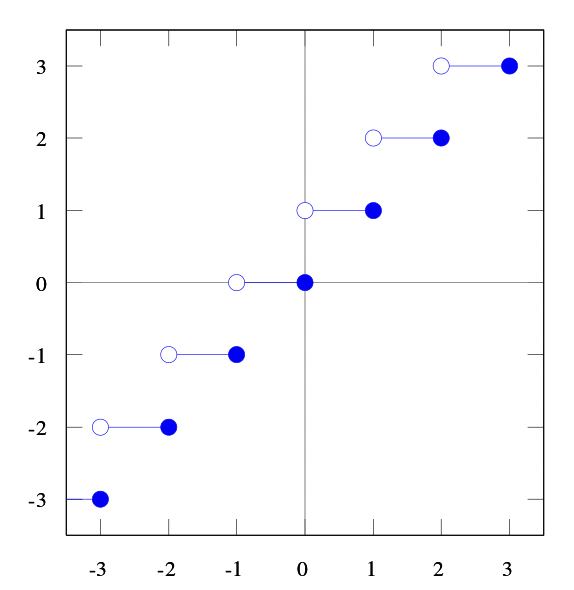
분수 부분 함수
fractional function
: 주어진 실수에서 최대 정수를 뺸 나머지 부분인 1보다 작은 실수를 구하는 함수
표기 : {x} or frac(x) ex) {5.25} = 0.25, {-5.25} = -0.75, {5} = 0
바닥함수, 천장함수,분수 부분 함수 관계
cf) 삼각 부등식 : 임의의 삼각형의 두 변의 길이의 합은 나머지 한 변의 길이보다 크다는 것.
멱등 법칙
: 연산을 여러번 적용하더라도 결과가 달라지지 않는 성질
바닥함수, 천장함수, 분수 부분 함수 모두 멱등 함수A의 모든 원소 x에 대해 f(f(x)) = f(x) 인 성질