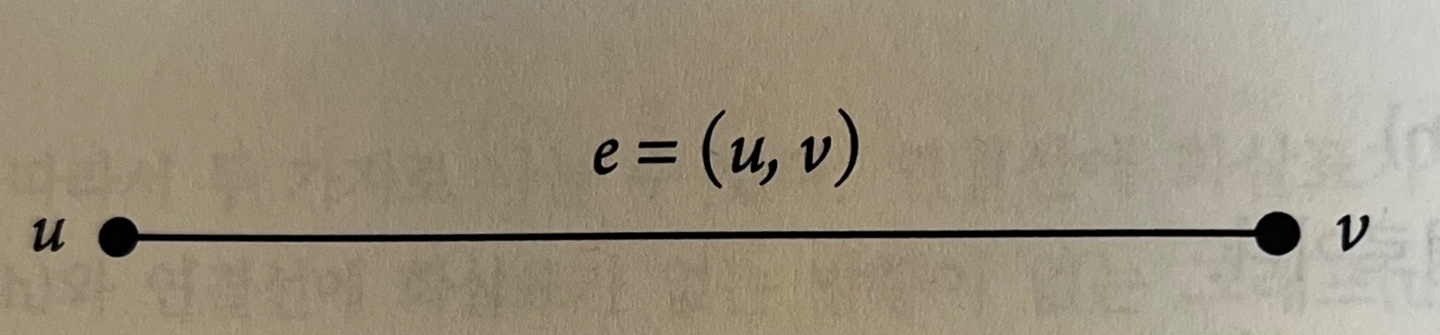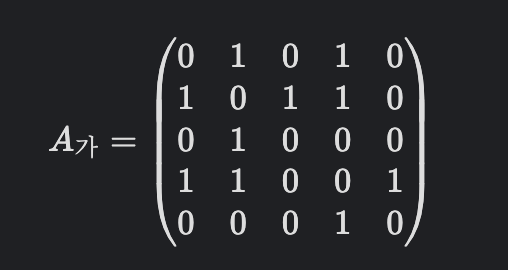이산수학 : 그래프 이론

김지원·2023년 4월 19일

목록 보기

8/11

그래프 이론

Graph theory

18세기 스위스 출신의 수학자 오일러에 의해 시작됨.

초기 : 수학이나 기하학의 영역으로 출발

확대 : 컴퓨터 공학 분야

장점 : 여러 자원들이나 도시들 간의 연결 상태를 추상화하여 나타낼 수 있다.
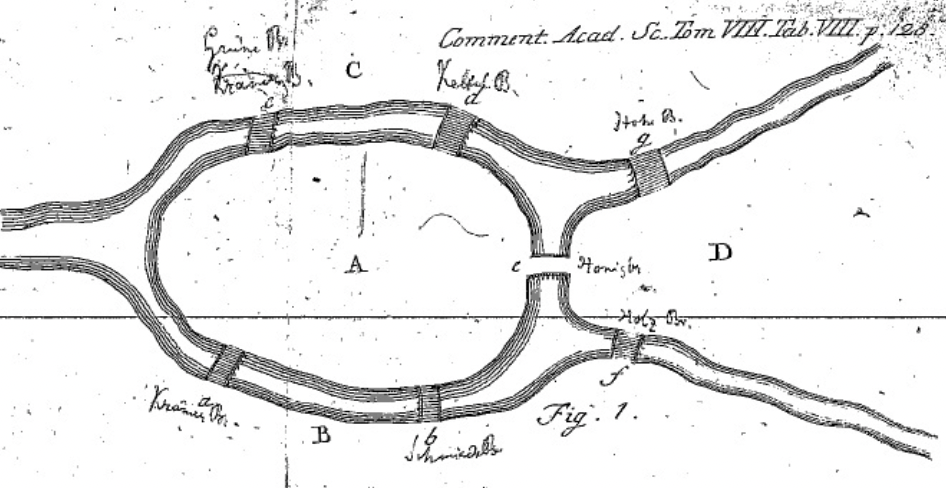
ex) 전기회로망이나 분자 구조식을 표현하는 영역에서 사용
예시) 쾨니히스베르크 다리 문제
: 임의의 지점에서 출발해 일곱 개의 다리를 한 번씩만 건너서 원래 위치로 돌아오는 방법
한붓그리기(traversable) 에서 유명한 문제이다.
- 그래프에서 연필을 떼지 않고 모든 연ㅇ결선을 오직 한번만 지나가게 그리는 것.
- 연결된 그래프에서 한붓그리기가 가능하려면 시작하는 정점과 끝나는 정점을 제외한 모든 정점의 차수가 짝수여야 한다.
cf) 차수 : 어떤 정점에 인접하는 연결선들의 개수 s
많은 사람들이 이 문제의 답을 찾기 위해 노력하였고 결국 오일러가 그래프를 이용해 이것이 불가능하다는 것을 증명했다.

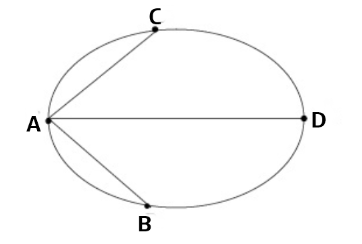
A,B,C,D를 정점(vertex) 라 하고 정점을 연결하는 선을 연결선(edge) 라고 한다.

방향 그래프(directed graph) : 연결선에 화살표가 있어 진행 방향이 있는 그래프
그래프(undirected graph) : 방향이 없는 그래프

그래프의 용어

그래프 G는 정점(vertex) = 노드(node) 들과
이들을 연결하는 연결선(edge) = 간선들로 이루어짐
G = (V,E)
V : 정점들의 집합
E : 연결선들의 집합, 두 정점의 순서쌍으로 표현
같은 간선을 한번만 지나는 길 : 경로(Path)
→ 길(Length) : 경로 또는 사이클(Cycle)을 구성하는 간선의 수

1) 경로(Path)

: 그래프에서의 경로는 정점들을 나열한 열 v1,v2,...vn 에서 모든 1 <= k <= n 에 대해 간선 (vk, vk+1) ∈ E 이 존재하는 경우.
→ 경로의 길이 = n - 1

두 개의 정점 사이를 잇는 간선들을 순서대로 나열.

2) 단순 경로(simple path)

: 간선이 겹치지 않는 경로

3) 기본 경로(elemnetary path)

: 정점이 겹치지 않는 경로

4) 사이클(cycle) 또는 순환(circuit)

: 경로v1,v2,...vn 에서 시점 v1과 종점 vn이 일치하는 경우

5) 단순 사이클(simple cycle)

: 같은 간선을 반복해 방문하지 않는 사이클

6) 기본 사이클(elementary cycle)

: 시작 정점을 제외한 어떠한 정점도 반복하여 방문하지 않는 사이클

루프(loop)

: 단 하나의 정점만을 연결하는 연결선
그래프 : (v,v), 방향그래프 : <v,v> 형태의 연결선

인접 adjacent 근접 incident
차수 degree

정점 u와 v를 연결한 간선 e = (u,v) 가 있을 때
정점 u와 v는 서로 인접하고 간선 e는 두 정점에 근접한다.

정점 u의 차수(degree) : u에 인접한 간선들의 개수
차수 = d(u) 혹은 deg(u) 로 표시
차수가 같다면 "동일차수"라고 한다.

그래프에서 정점들 간의 연결 여부에 따라 다르게 정의된다.

연결 그래프(connected graph)
: 그래프의 모든 정점들이 연결되어 있을 때

강한 연결 그래프(strongly connected graph)
: 두 정점 v와 u에 대해 v → u의 경로와 u → v의 경로들이 존재할때의 그래프
특히 방향 그래프에서만 의미가 있다.

연결 요소(connectivity component)
: 모든 정점들이 연결되어 있는 부분

연결수(connectivity number)
: 그래프 G에서 연결 요수의 개수

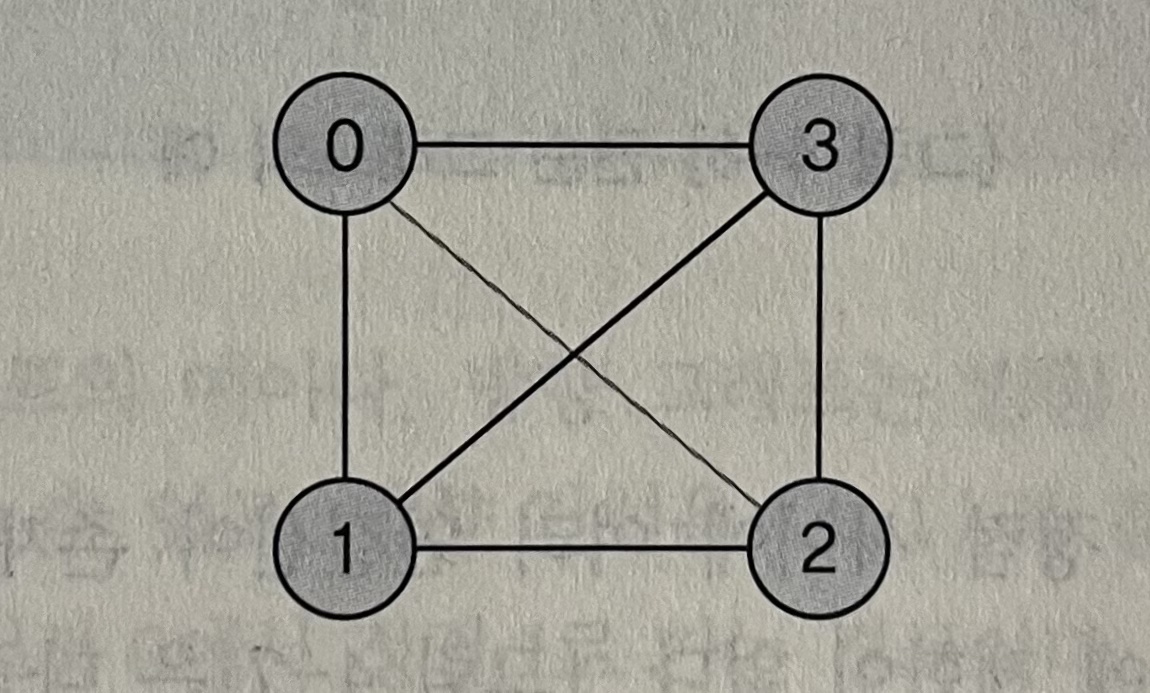
방향그래프

G = <V,E> 
V = {0,1,2,3}
E = {<0,1>, <0,3>, <2,3>, <3,1>}
	  ↑ 선행자   ↑ 후행자
방향 간선(undirected edge) 만 사용한다.

방향 그래프는 간선을 통해 한쪽 방향으로만 갈 수 있다.
<v,w> v → w
정점 v를 정점 w의 선행자(predecessor) 라 하며
정점 w를 정점 v의 후속자(successor) 라고 한다.

진입 차수(In degree) : 정점 v를 머리로 하는 간선의 수

진출 차수(Out degree) : 정점 v를 Rh리로 하는 간선의 수

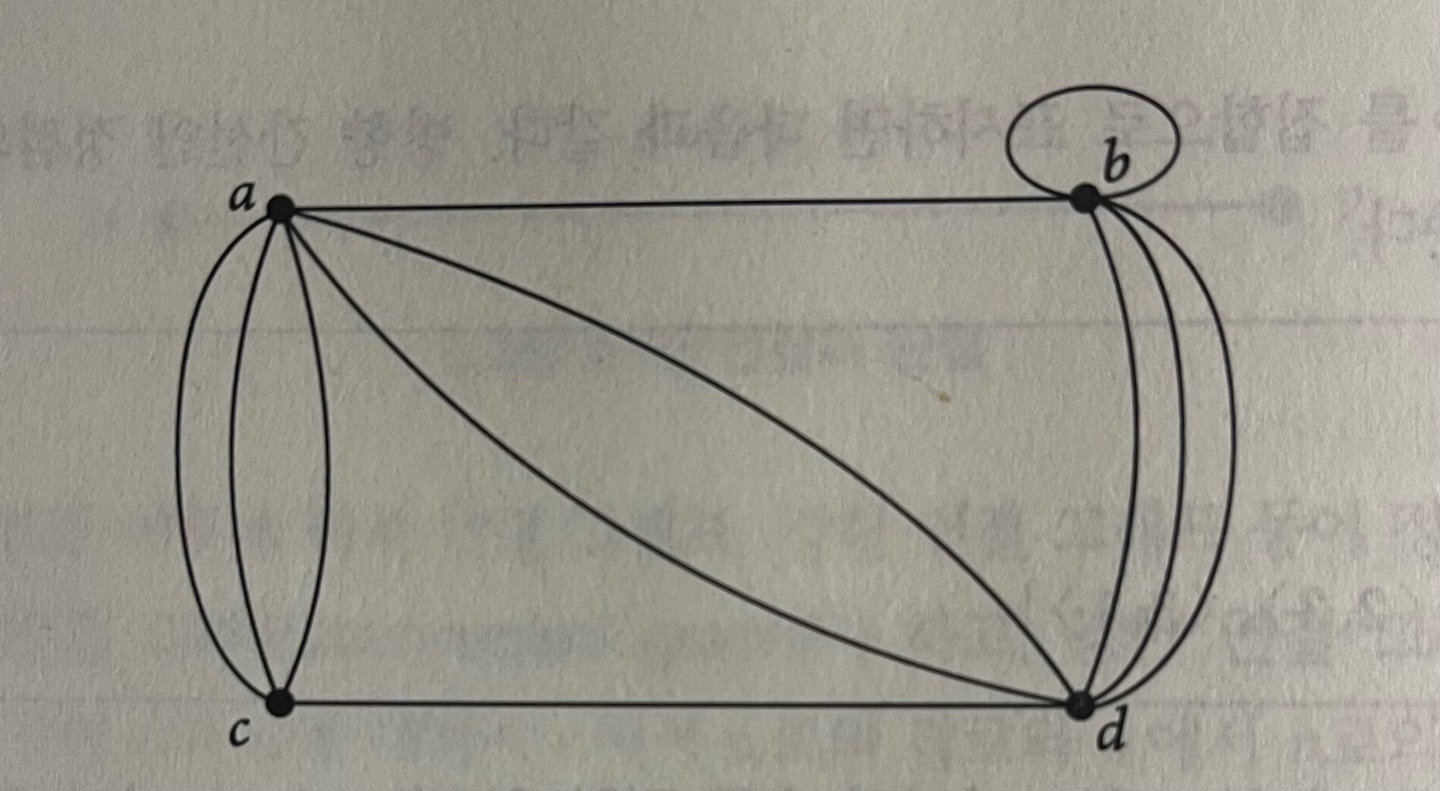
단순 그래프

simple graph

: 두 정점 사이에 연결이 하나 이하로 존재하는 그래프

하나의 정점이 자기 자신으로 연결되는 선(=loop)이 존재하지 않는다.

다중 그래프

multi graph

: 두 정점 사이에 여러 연결선이 존재할 수 있는 그래프의 일반화

연결선 개수(간선의 개수)는 제한이 없다.

가중치 그래프

weighted graph

: 간선에 비용이나 가중치가 할당된 그래프, 네트워크(network)라고도 한다.

간선에 값을 가진다.

최소 비용 신장 트리, 최단 경로 문제, 위상 순서, 임계 경로 등에 활용된다.

완전 그래프

complete graph

: n개의 정점으로 구성된 그래프에서 간선 수가 최대인 그래프

최대 간선의 수 : n(n-1)/2 개

방향 그래프에서 최대 간선 수 : n(n-1) 개

n개의 정점으로 구성된 완전 그래프는 Kn으로 표기함.

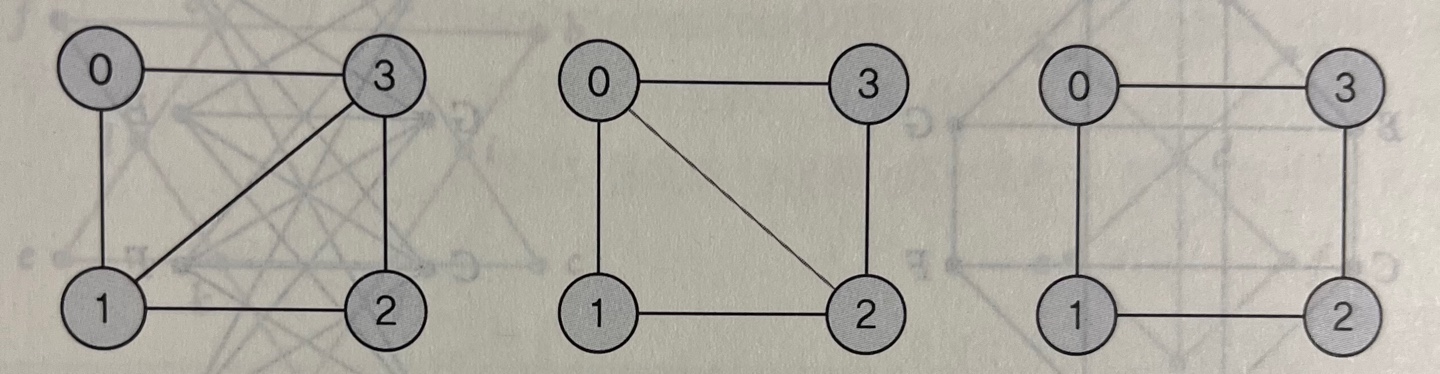
부분 그래프

sub graph

: 그래프 G를 구성하는 정점 일부와 간선들 중 일부를 그린 그래프
G의 부분 그래프 => V(G') ⊆ V(G), E(G') ⊆ E(G) 인 그래프 G'

부분신장 그래프

spanning graph

: 그래프 G의 정점은 모두 포함하지만 간선의 일부가 없는 그래프
G의 부분신장 그래프 => G = (V,E)에서 V' = V 이고 E' ⊆ E인 그래프 G'

정규 그래프

regular graph

: 모든 정점의 차수가 같은 그래프

각 정점의 차수가 모두 k인 경우 k-정규 그래프로 표기한다.

이분 그래프

bipartite graph

: G = (V,E)에서 정점 집합 V가 V = V1 ∪ V2 와 V1 ∩ V2 = ∅ 을
만족하는 두 집합 V1, V2로 분리되고
그래프의 모든 간선이 V1의 한 정점에서 V2의 한 정점으로 연결되는 그래프

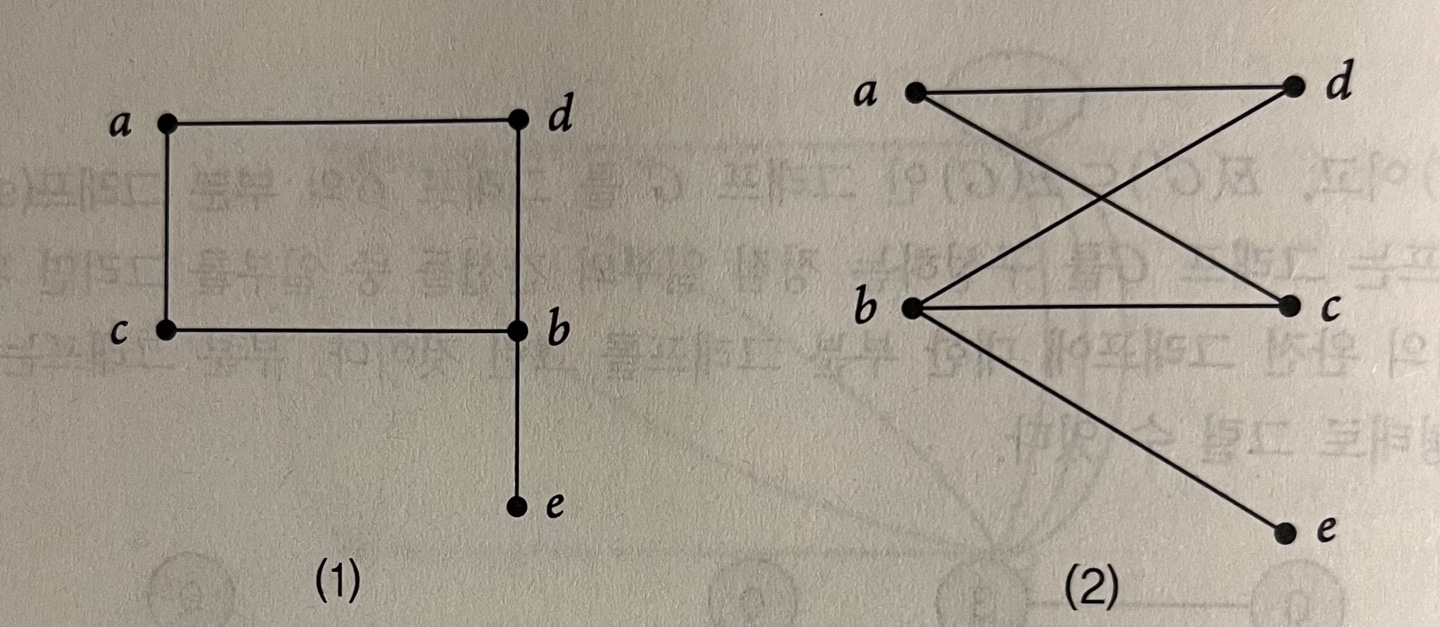
v1, v2 각 그룹내에선 간선이 존재하지 않음.
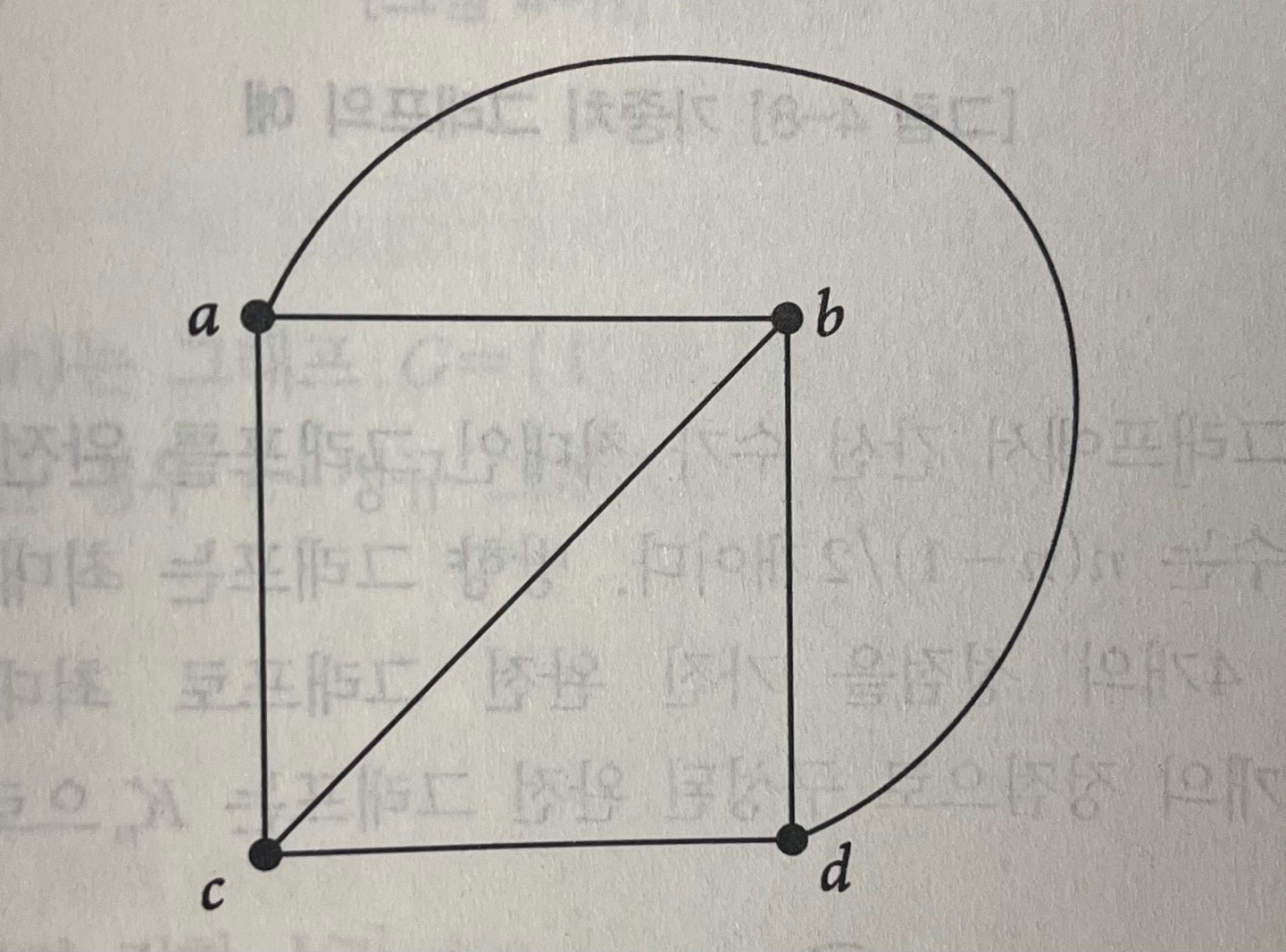
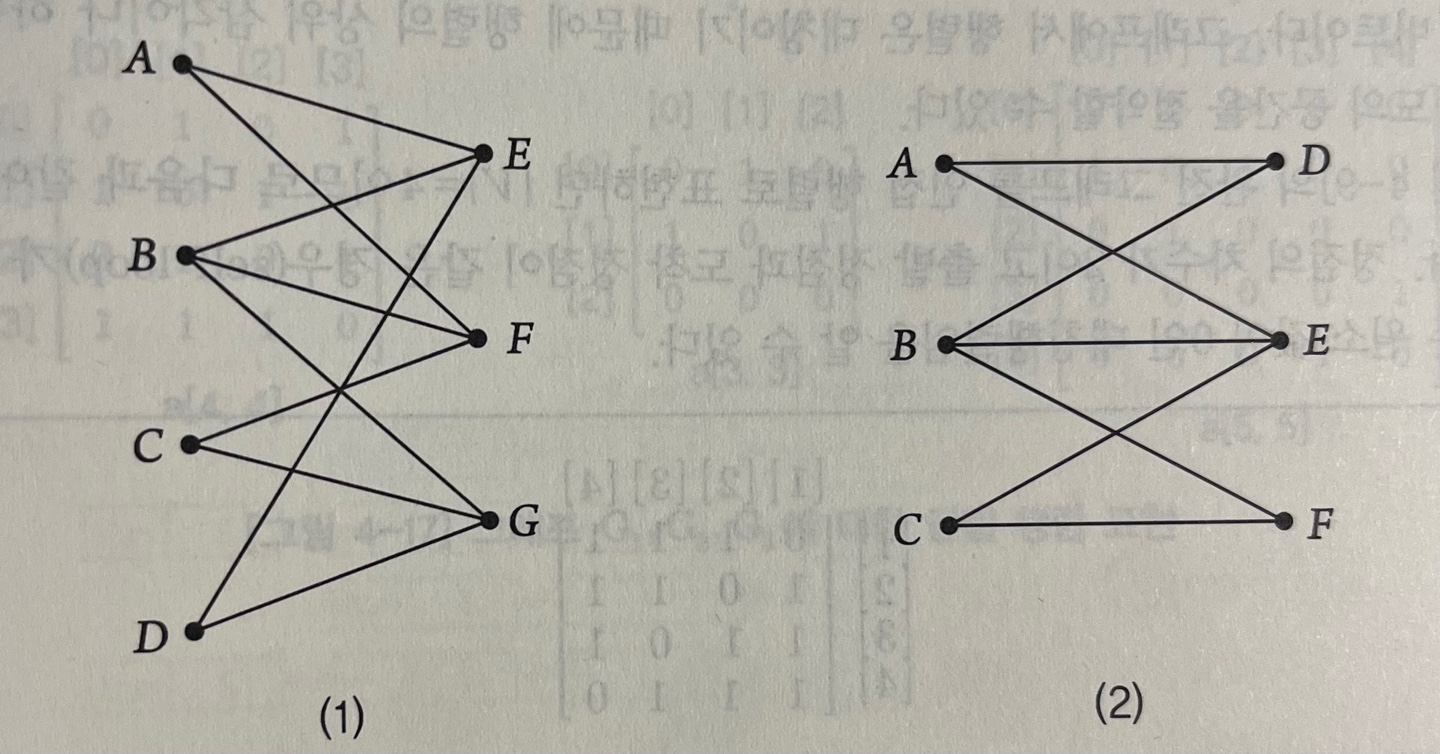
(1)에서는 V1 = {a,b} 와 V2 = {c,d,e} 로 나누어 질 수 있음으로
(2)처럼 이분 그래프로 그릴 수 있다. 

완전이분 그래프

Complete bipartite graph

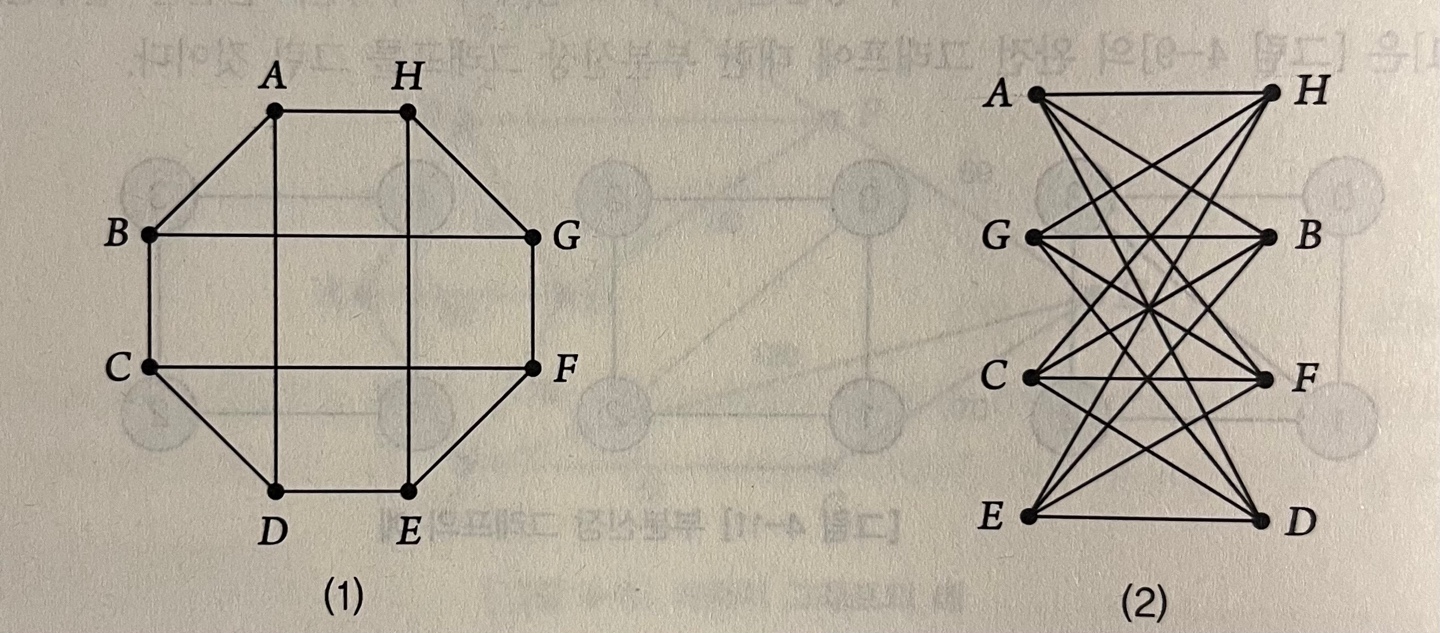
: 이분 그래프 G = (V,E)에서 V1의 모든 정점과 V2의 모든 정점 사이에 간선이 있는 그래프
v1정점의 개수 : |V1| = m
v2정점의 개수 : |V2| = n
완전이분 그래프 : Km,n 표기
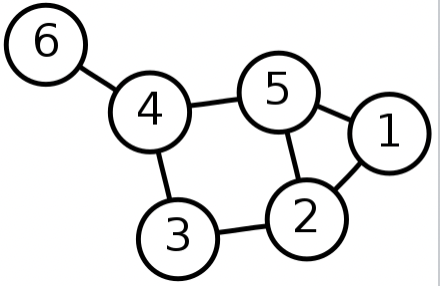
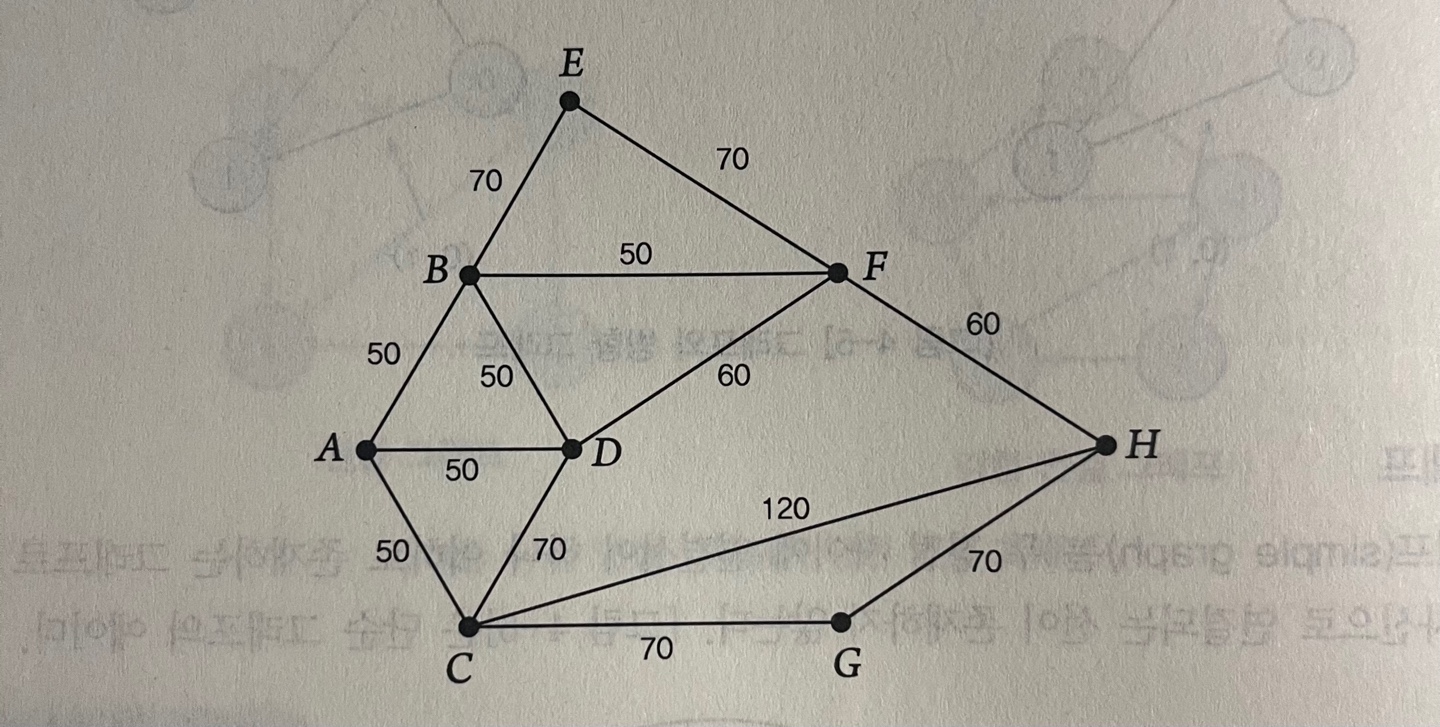
(2)처럼 V1 = {A,G,C,E} V2 = {H,B,F,D} 로 나누어지는 이분 그래프로 그릴 수 있다. 
완전이분 그래프 K4,4 이다.

오일러 사이클

오일러 경로

Euler path = 한붓그리기 문제

: 정점은 여러번 지날 수 있지만 그래프의 모든 간선을 단 한번씩만 통과하는 경로
오일러 사이클(회로) = 시작점과 도착점이 같은 오일러 경로
오일러 그래프 : 오일러 사이클을 지닌 그래프

오일러 경로 존재여부 판단 방법

무방향 그래프

차수가 홀수인 정점 2개

차수가 홀수인 정점 0개 → 오일러 회로

그래프가 오일러 사이클을 가질 필요 충분 조건

연결된 그래프

모든 정점의 차수 짝수

오일러 사이클이 아닌 오일러 경로가 있을 필요 충분 조건
= 시작 정점 끝나는 정점이 다른 경로 일 때

정확히 두 개의 정점만이 홀수의 차수를 가짐

그래프가 연결되어 있음

홀수 차수가 2개인 그래프 : 한 홀수 점은 출발점, 다른 홀수 점은 종착점.

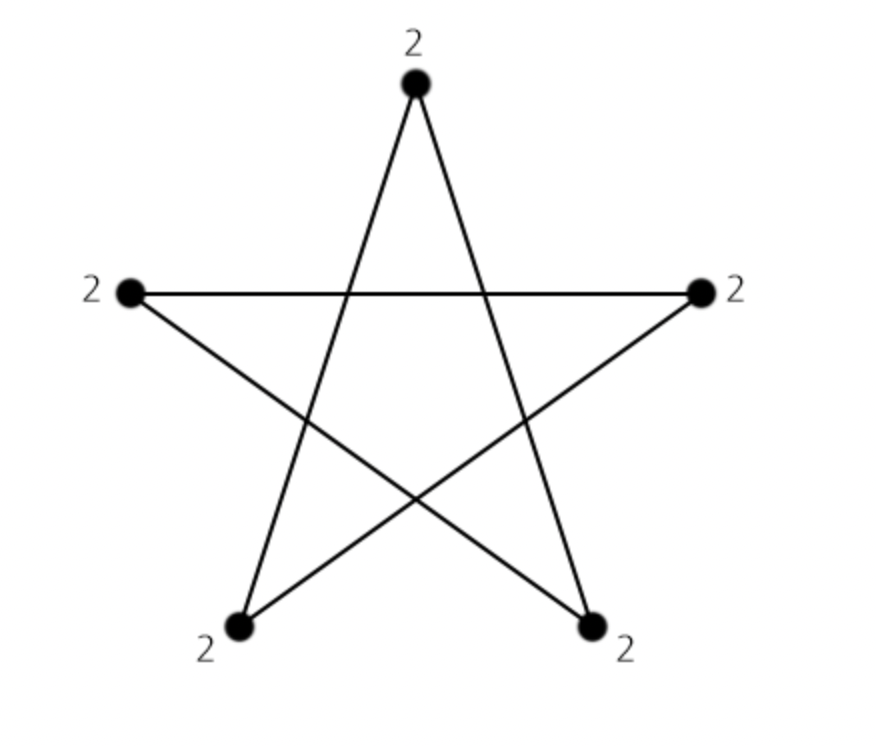
한붓그리기

가능한 조건
1) 차수가 홀수인 정점이 하나도 없는 경우 = 오일러 사이클
시작점 = 도착점 
2) 차수가 홀수인 정점이 두 개 있는 경우 = 오일러 경로
시작점 != 도착점 / 시작점과 도착점만 홀수 인 경우랑 같은 말.
죽 차수가 홀수이 정점이 세 개 이상이면 한붓그리기 불가능

정점 u에서 출발 정점 v에서 끝나던지 그 반대의 경우에서만 가능하다.

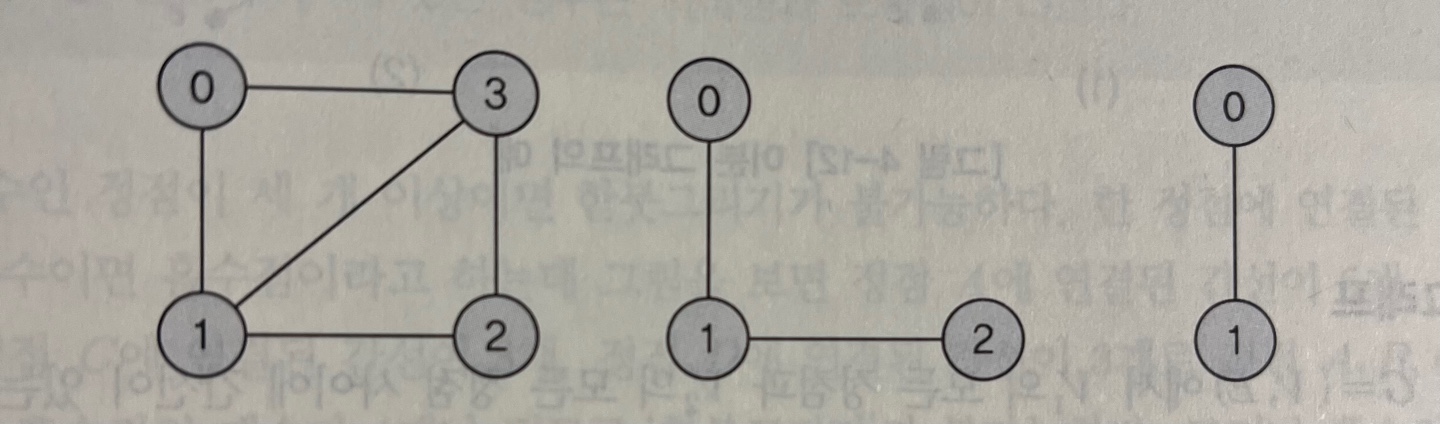
어느 곳에서 시작하던 다시 시작점으로 되돌아 오게 되어있다. 즉, 오일러 사이클, 회로가 존재한다는 것이다.

모든 정점들의 차수가 짝수(2) 인데 이것은 시작, 끝점을 제외하고 들어오는 간선이 있으면 나가는 간선이 있다는 것을 의미한다.
→ 오일러 경로는 존재하지만 오일러 회로는 존재하지 않는 그래프이다.

❗️ 따라서 그래프 이론에서는 주어진 그래프에서 원하는 경로나 사이클을 찾는 문제를 해결하는 방법을 찾는게 중요하다.

해밀턴 경로
Hamitonian Path

: 그래프의 모든 정점을 한 번씩만 방문하는 경로
해밀턴 회로(순회, 순환) : 정점 V에서 시작해 모든 정점을 한번씩 방문하고 다시 정점 v로 돌아오는 회로

G(V,E) 가 오일러 그래프이자 해밀턴 그래프 일 때

오일러 그래프의 길이 : n(E(G)) : 간선
해밀턴 회로의 길이 : n(V(G)) : 정점

오일러 그래프와 해밀턴 그래프 사이는 관계가 없다.

그래프 표현 방법

그래프를 컴퓨터 프로그램으로 구현하기 위해 인접 행렬이나 인접 리스트를 이용한다.

인접 행렬 = 부속행렬

adiacency matrix = incidence matrix

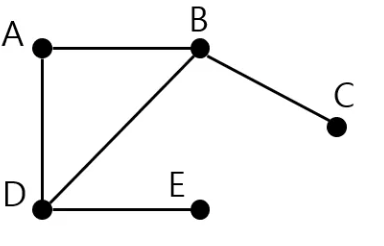
: 그래프의 모든 정점을 행과 열의 원소로 표현
두 정점 사이에 연결하는 간선이 존재하면 행렬에 해당하는 원소의 값 = 1
두 정점 사이에 간선 존재 x 행렬에 해당하는 원소의 값 = 0
n>=1개의 정점을 가진 그래프에 대해 |V|=n 일 때 크기가 n X n인 정방 행렬 A로 나타내어지며, 이때 A의 원소 aij(i=행, j=열)는 컴퓨터 프로그래밍에서는 2차원 배열 a[n,n]으로 표현한다.
그래프 |V|= n인 그래프 인접 행렬 표현시 필요한 공간 = n^2비트(정점의 갯수의 제곱)
그래프에서 행렬은 대칭임으로 행렬의 상위 삼각이나 하위 삼각만 저장한다면 반 정도의 공간을 절약할 수 있음.

인접행렬의 정보

: 간선이나 아크(방향 그래프 간선)의 존재 여부

그래프의 인접 행렬에서 행 i과 열 i의 합은 동일하며 정점 i의 차수이다.

정점 i의 진출 차수(Out degree) : 행 i의 합

정점 i의 진압 차수(In degree) : 열 i의 합

인접 리스트

adiacency list

: 그래프를 구성하는 모든 정점들에 대하여
간선으로 연결되어 있는 정점들을 연결 리스트로 나열한 것.
즉, 각 정점에 대해 포인터를 가진 노드가 주어지고 그 정점으로부터 연결된 정점들을 차례로 연결리스트로 표현한 것이다.

같은 리스트 내에서 순서는 의미가 없다.

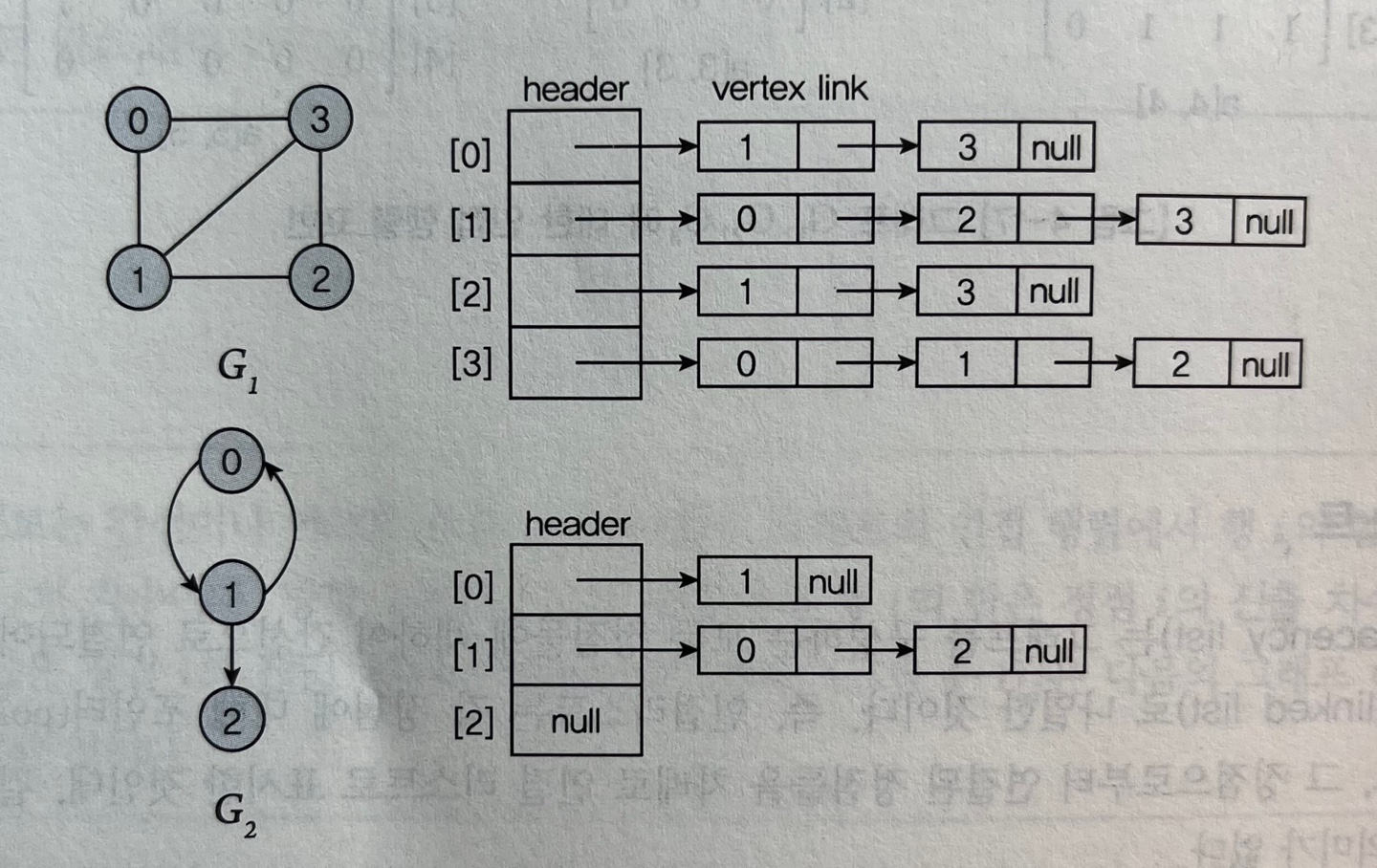
연결 리스트로 구현한 인접 리스트

노드의 연결로 표현
							해당 정점 다음에 따라오는 노드의 주소 가르킴(포인터 필드)
							  ↓
헤드 노드 + 리스트 노드 (정점필드 + link필드)
 ↑					 ↑ 
 ↑                  그래프의 정점 값 저장    
연결된 정점의 주소를 가르키는 한 개의 포인터 필드를 가지는 노드                    
각 노드는 헤드라고 불리는 시작 노드와 연결된 인접 노드를 갖는다.

마지막 노드의 포인터 필드 : NULL값을 저장, 데이터의 마지막임을 표시함.