최단 경로
: 가중치 그래프에서 여러 경로 중에서 가중치의 합이 가장 작은 경로
모든 간선의 가중치의 합 : 그래프의 가중치
- 다양한 경로 중 가장 효과적이고 경제적인 경로를 찾는 문제에 활용
- 최단 경로를 구하기 위해서 많은 경우의 수를 고려해야 하며 그래프가 크고 복잡한 경우 계산량이 많아질 수 밖에 없음.
다익스트라 알고리즘
Dijkstra algorithm
: 최단 거리를 가지는 최단 경로를 구하는 알고리즘
- 출발점으로부터 거리가 최소로 알려진 점들의 집합 S를 유지하면서 가장 짧은 거리를 가지는 나머지 정점 v를 차례로 S에 포함
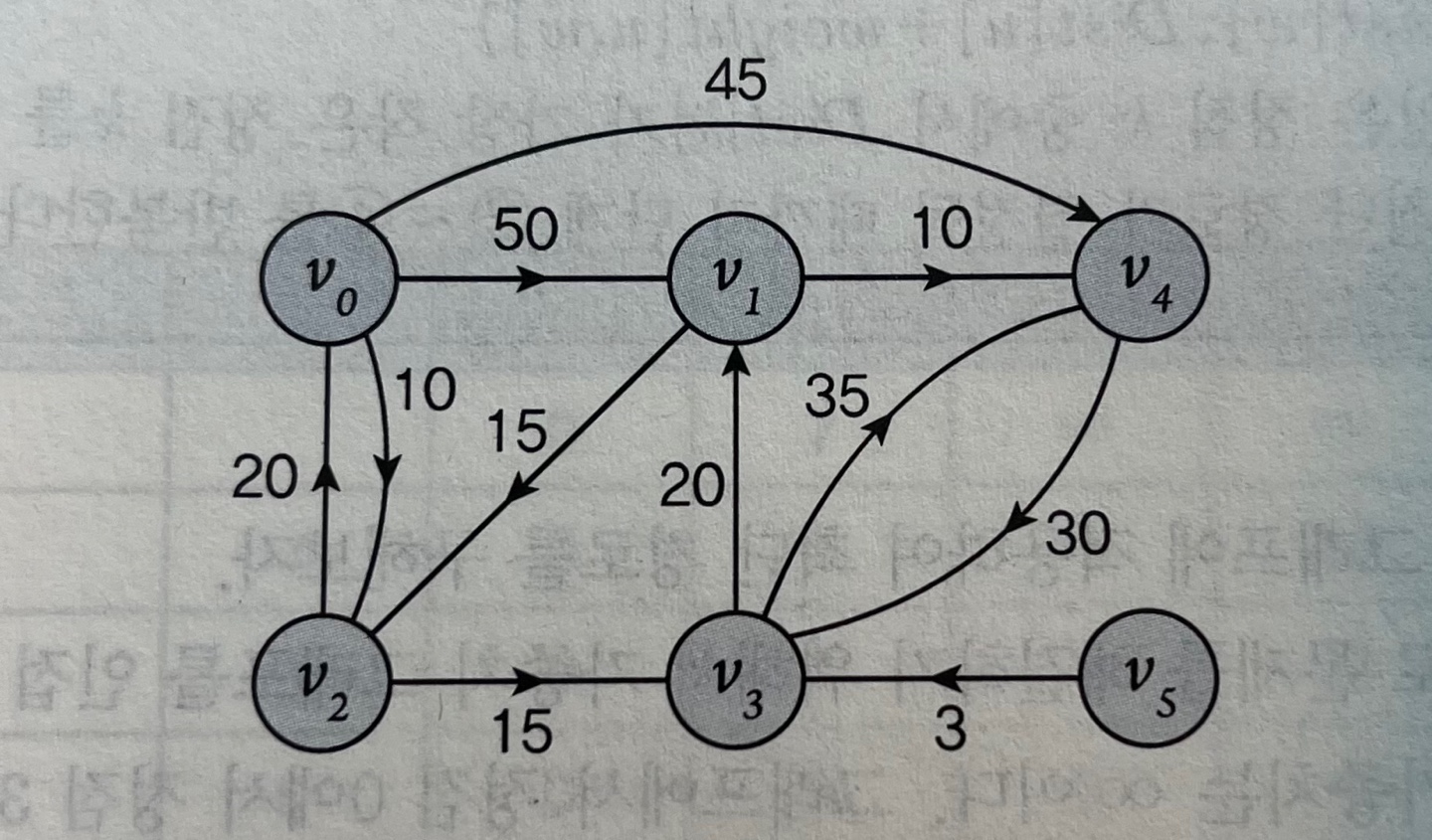
1) 주어진 방향 그래프 G = <V,E>에서 V={1,2,,...,n} 정점 {1} : 출발점 2) 정점 i에서 j로 가는 거리 : C[i,j] 만약 i에서 j로 바로 가는 경로가 없으면 거리는 무한대가 된다. 3) D[i] : 출발점에서 현재 점 i에 이르는 가장 짧은 거리
다익스트라 알고리즘 실행 단계
1) 처음 S[]에 시작점 v를 저장. → Dist[v] = 0, Dist[i] = weight[v,i] ↑ 거리가 자기자신이니 0 : 어떠한 정점 v에서부터 i까지의 거리 = v, i점까지 가중치2) 가장 최근에 S[]에 첨가한 정점을 u로 설정3) u의 모든 인접 정점 중에서 S[]에 포함되지 않은 정점 w에 대해 Dist[w]를 다시 계산 → Dist[w] = min(Dist[w], Dist[u] + weight[u,w]) : u와 w 거리 중 가장 짧은 것4) S[]에 포함되지 않은 정점 k 중에서 Disk[k]가 가장 작은 정점 k를 S[]에 추가한다.5) 모든 정점에 대한 최단 경로가 결정될 때까지 2 ~ 4 를 반복.
다익스트라 알고리즘 예시
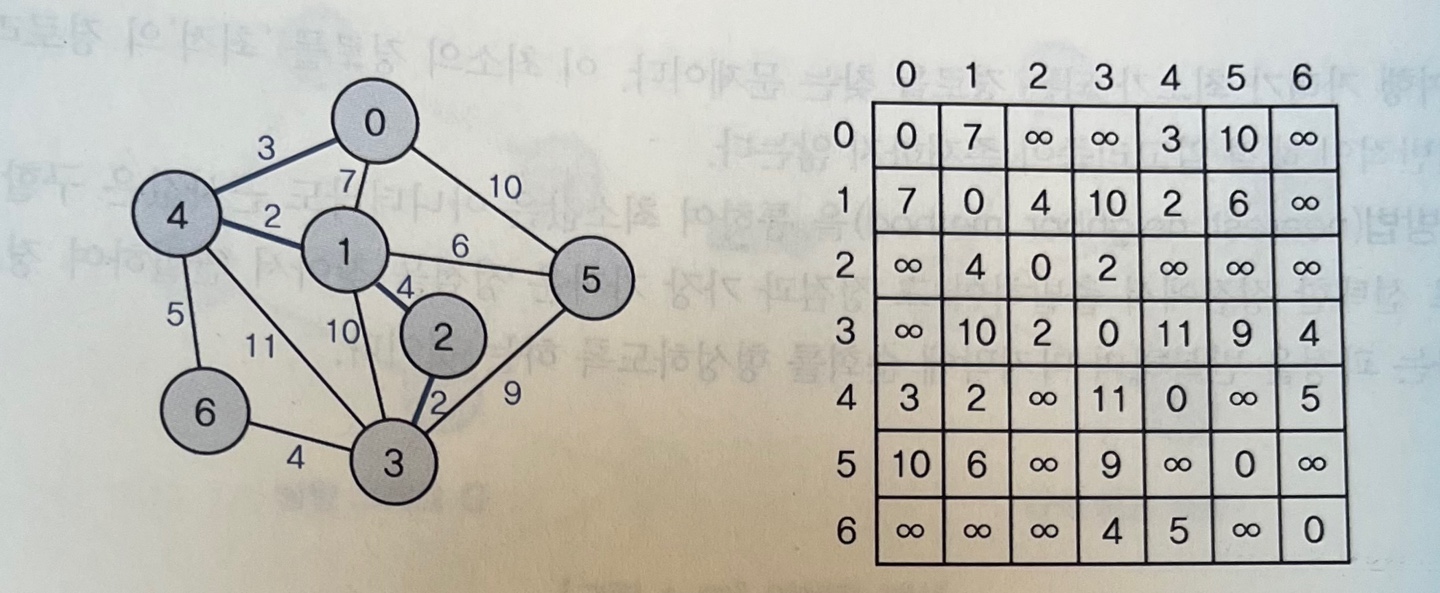
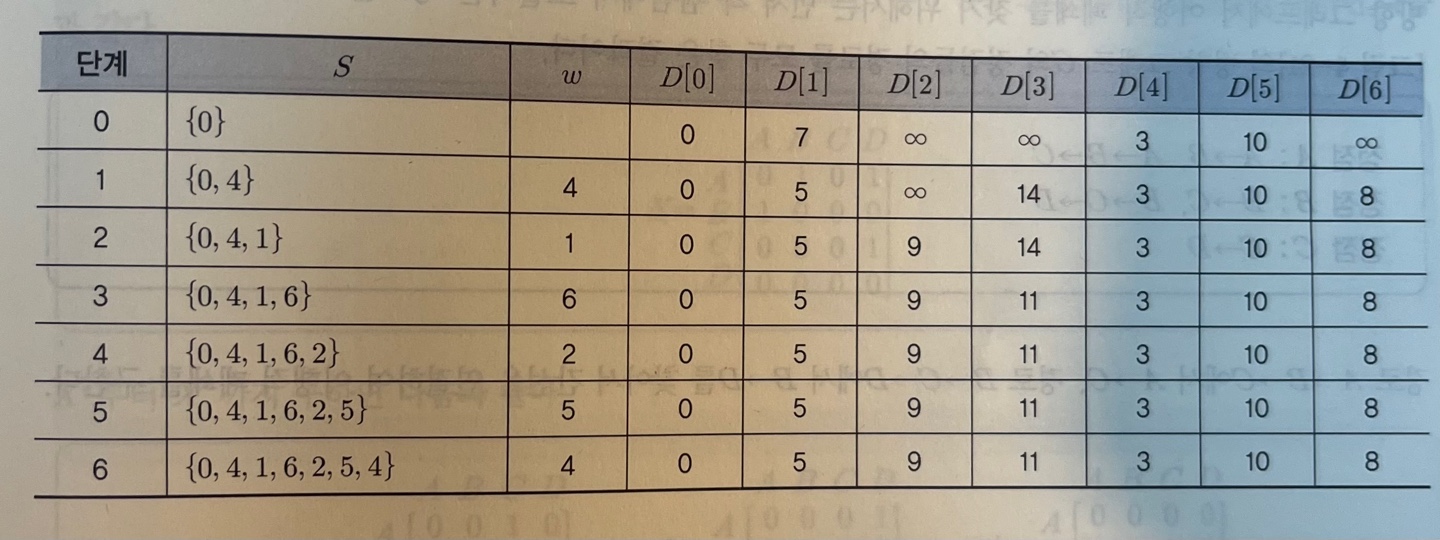
1단계S = {0} D[1] = 7 D[2] = ∞ D[3] = ∞ D[4] = 3 D[5] = 10 D[6] = ∞ 임으로 D[4] = 3 → w = 4 일때 제일 최소라서 최소의 D값을 가진 정점으로 선택2단계
먼저 1로 가는 최소 경로를 찾아보자. 0을 지나 최소의 D값으로 설정한 4를 지나 1로가는 최소 경로는 0 → 4 → 1 : 3 + 2 = 5가 된다. 나머지 경로도 같은 방법으로 찾으며 S의 영역을 넓혀준다.
해밀턴 순환 응용 문제로는 순회판매원 문제(Traveling salesperson problem)이 있다.
방문해야 할 도시와 이들 사이의 거리가 주어졌을 경우, 순회판매원이 어떤 특정한 도시를 출발해 어떠한 도시로 두 번 방문 없이 모든 도시들을 거쳐 처음 출발한 도시로 돌아올때 총 여행 거리가 최소가 되는 경로를 찾는 문제
경로의 존재
<배경>
방향 그래프는 정점을 연결하는 간선에 방향성을 부여해 간선을 화살표로 표시한다.
그래서 방향 그래프는 어떤 두 정점 간에 연결될 수 있는가(connectivity)를 확인할 수 있다.
도달 가능성
reachability
한 정점에서 연결되는 모든 정점을 찾아보는 문제
깊이 우선 탐색이나와샬 알고리즘을 통해이행적 폐쇄를 찾는 방법으로 해결할 수 있다.
이행적 폐쇄 = 추이 클로져
Transitive Closure
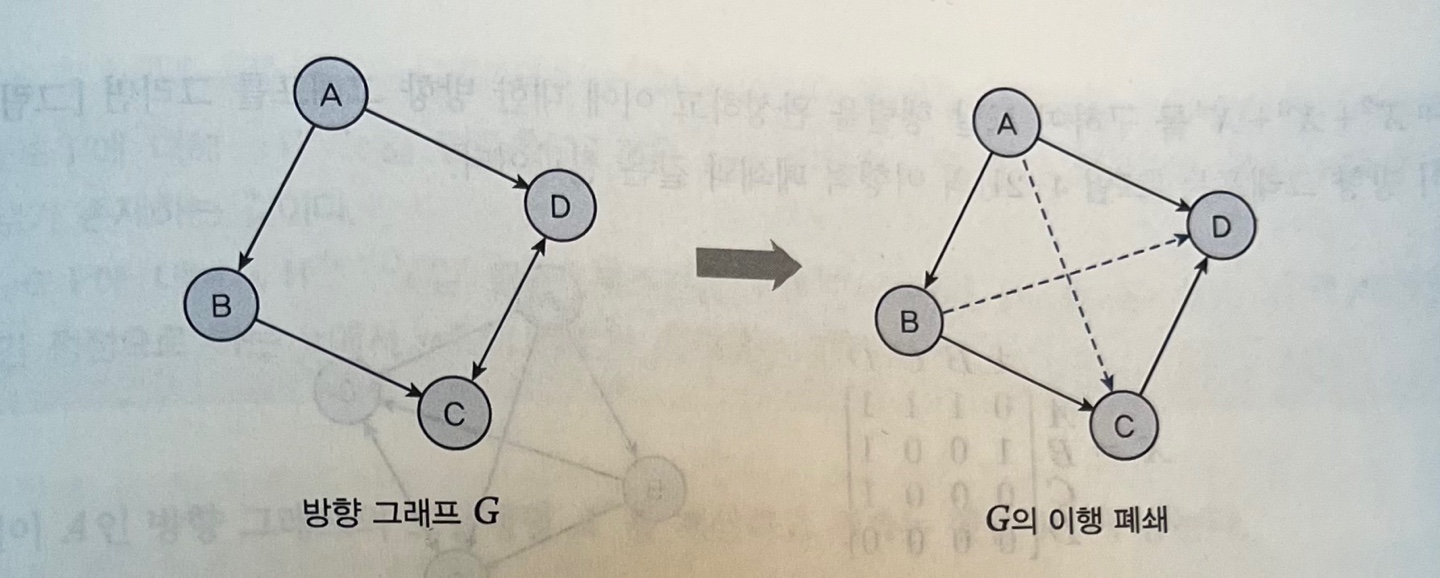
: 어떤 정점 A에서 C로 가는 직접경로는 없고 우회경로가 있을 때 A → C로의 간선을 연결한 그래프.
- 방향 그래프에서 이행적 폐쇄를 찾기 위해서는 먼저 각 정점에 도달하는 경로를 모두 찾는다.
경로 A → B → C 에서 A → C 경로를 찾았고 경로 B → C → D 에서 B → D 경로를 찾을 수 있다. - 간접 경로 : 점선으로 표시D+ : 이행적 폐쇄 행렬 D+[i,j] = 1 : 정점 i에서 j까지 길이가 0보다 큰 경로의 존재 유무 표현 D* : 반사 이행적 폐쇄 행렬 D*[i,j] = 1 : 정점 i에서 j까지 길이가 0이상인 경로의 존재 유무 표현
도달 행렬
reachability
G = <V,E>에서 정점 v1과 정점 v2를 연결하는 간선 <v1,v2>가 존재하면
v1에서 v2로 가는 길이가 1인 경로를 의미한다.
이때 길이가 1인 경로를 E^1로 표기하고길이가 n인 경로는E^n으로 표현한다.
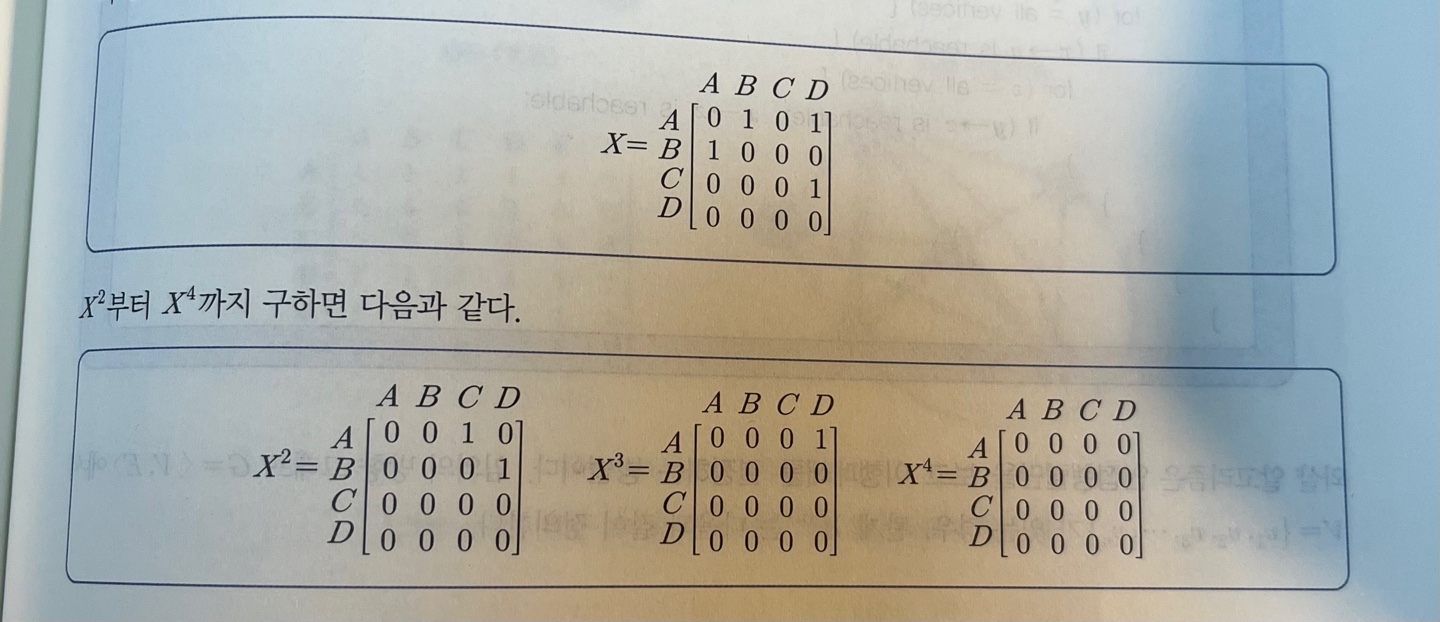
E* = E ∪ E2 ∪ E3 ∪ ...를 구해 두 정점 사이의 경로 존재여부를 확인 할 수 있다.E에 대한 인접행렬 = X / E*에 대한 인접행렬 = X* 이면 X* - X + X2 + ... + Xn이 성립한다.여기서 X*를
도달 행렬(reachability)라고 함
- 행렬 X에 대한 거듭제곱은
불곱(boolean product)연산- 행렬 X에 대한 합은
불합(boolean sum)연산
❗️ 즉, 도달 행렬은 방향 그래프에서 정점 간 경로의 존재 여부를 행렬로 표현한 것이다.
일일히 이렇게 하나씩 할 수 없음으로 알고리즘을 사용하자.
와샬 알고리즘
Warshall algorithm
: 한 노드에서 다른 노드까지의 도달가능성을 알아보는 알고리즘
- 정점 B가 A에 연결되어 있는 가를 확인하는 연결성의 문제 확인
경로가 존재하면 정점 A에서 B로 연결하는 간선을 추가- 인접 행렬 이용
인접행렬이 A인 방향 그래프의 도달행렬 A*를 계산하고 결과는 행렬 W에 남음.
✔︎ 와샬 알고리즘은 인접행렬만 보고 이행폐쇄를 결정하는 방법이다.
A → B와 B → C 를 만족하는 경로가 있으면 A → C 경로도 존재한다.
(자기 자신으로 가는 경로는 있다고 가정)
예시)
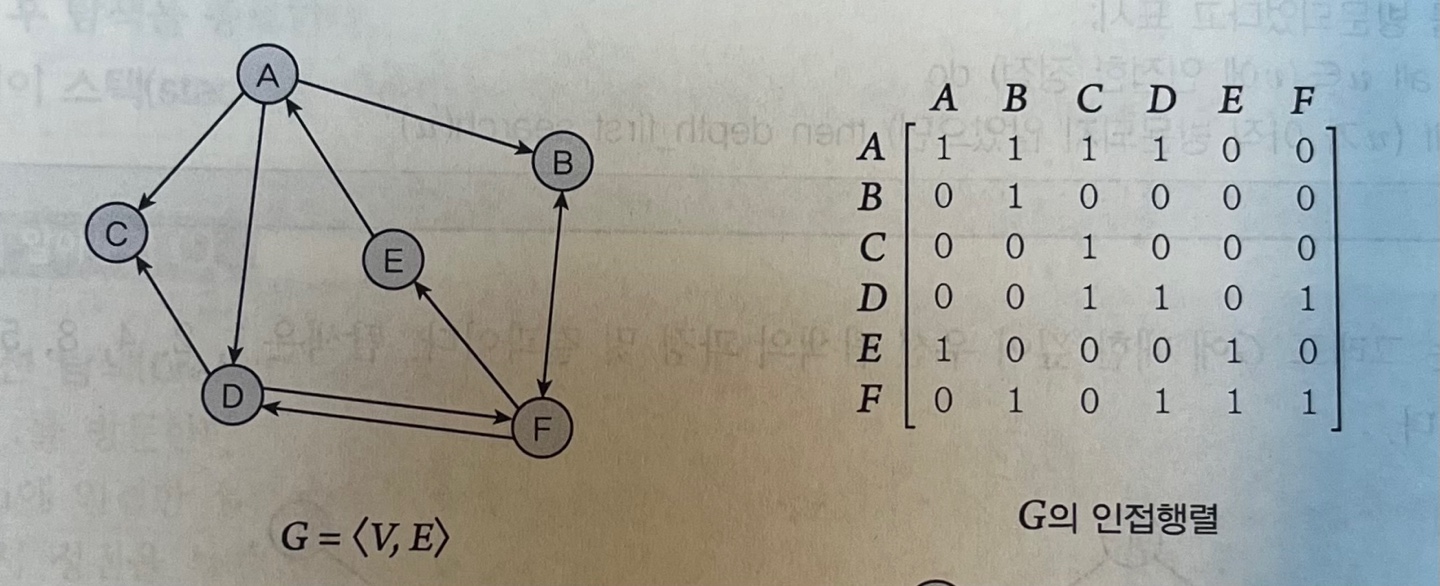
방향그래프 G = <V,E> V(G) = {A,B,C,D,E,F} E(G) = {<A,C>, <A,B>, <A,D>, <D,C>, <D,F>, <E,A>, <F,B>, <F,D>, <F,E>} 에 대해 샬 알고리즘을 이용해 이행적 폐쇄를 찾아보자
- 문제에 따른 방향그래프와 인접행렬 나타낸 것
- 자기 자신으로의 간선은 있다고 가정함으로 대각 요소는 모두 1이 된다.
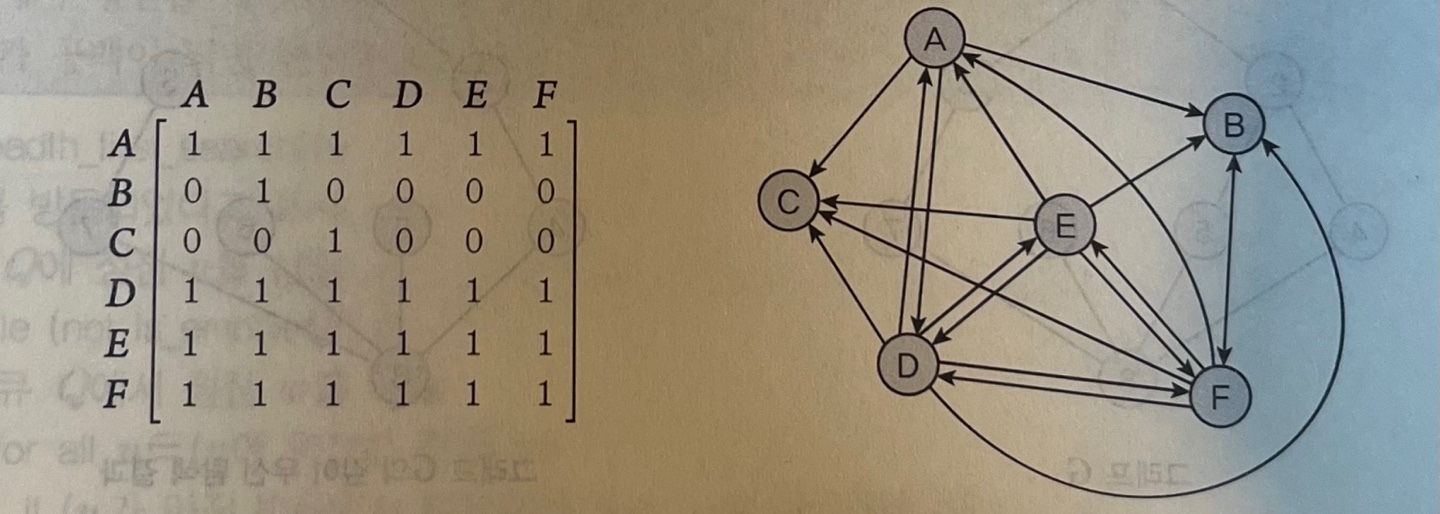
B -> F 화살표 xx값으로 G의 인접행렬에서 정점 A를 선택. A와 연결된 정점 B,C,D를 y로 두어 알고리즘 적용 → x값 : A / y값 : B,C,D 정점 B와 C는 뻗어나가는 화살표가 없으므로 추가 연결을 찾을 수 없다. D는 F로 뻗어나가기에 z값을 찾을 수 있게 된다. 따라서 인접행렬에서 정점 D에 연결된 정점 C와 F를 찾을 수 있으므로 ❗️ (A,F)의 인접행렬의 원소값을 0에서 1로 변경한다.
- 와샬 알고리즘을 모든 정점에 적용하면 이와 같이 이행적 폐쇄가 된다.
그래프에 연결된 모든 정점을 탐색하기 위해서 임의 정점을 선택하기보다 시작점을 기준으로 일정한 방향으로 탐색하는게 효율적이다.
깊이 우선 탐색 DFS
Depth First Search
- 시작점 v부터 방문하고 v에 인접한 정점 중 방문하지 않은 정점 w를 방문하고 다시 w로부터 탐색을 시작한다.
- 이미 방문된 정점일 경우에는 그 전에 마지막으로 방문한 정점으로 돌아가 반복한다.
- 스택을 사용한다.
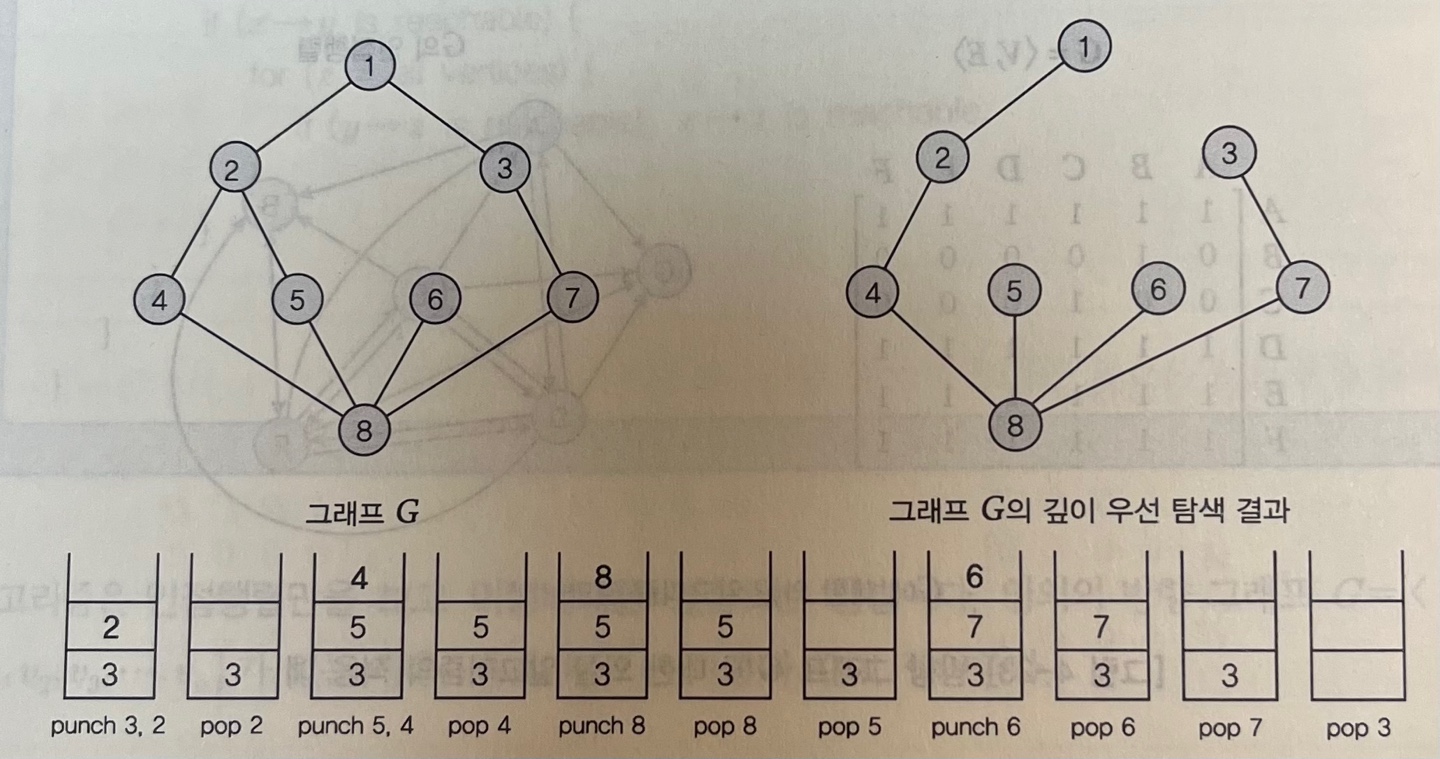
시작 정점 : 1 1과 연결된 모든 정점 2,3 스택에 저장 스택에서 2를 꺼내어 1과 연결 2를 시작점으로 위의 과정을 반복한 것. 스택이 공백이 되면 연산 종료
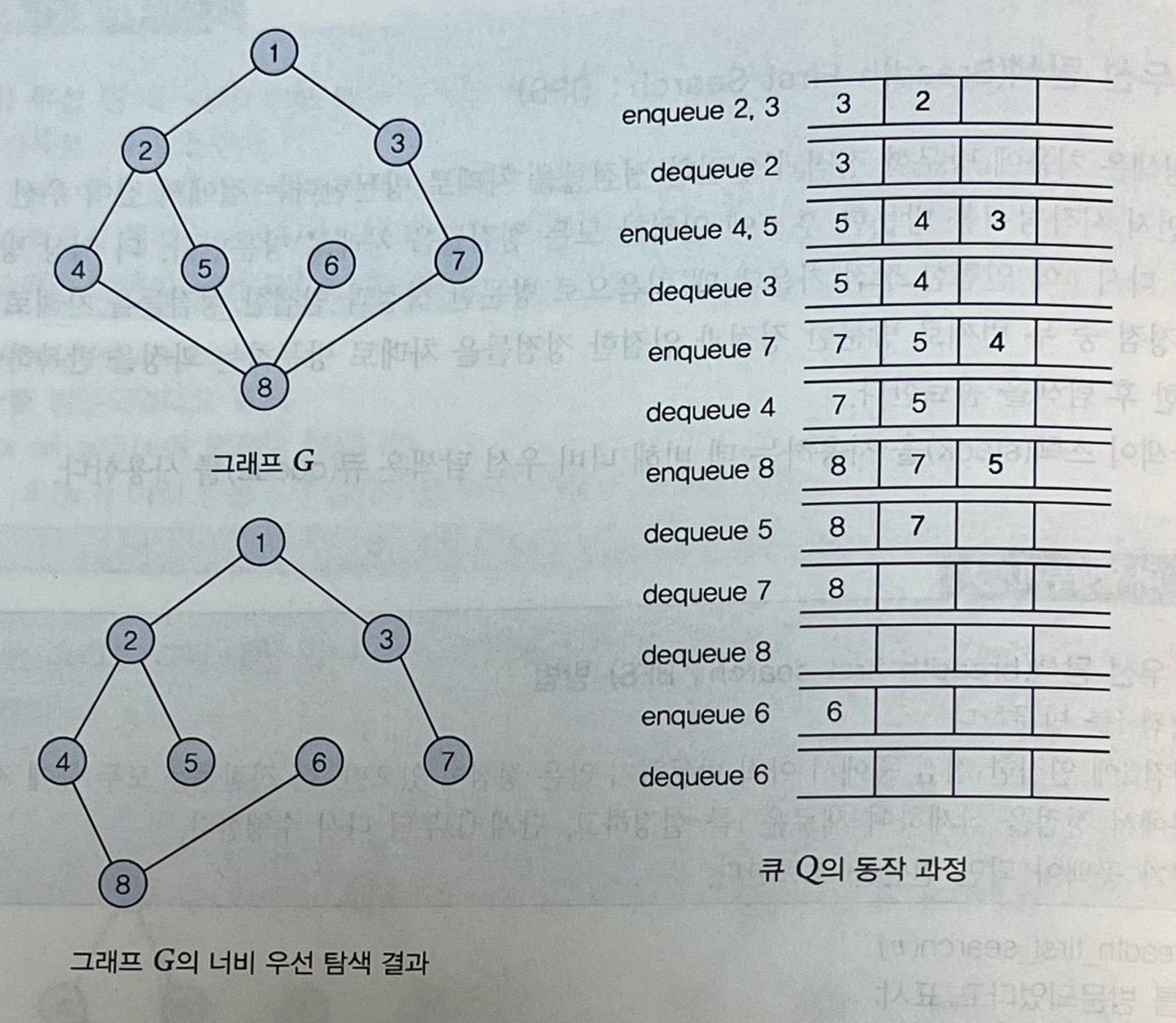
너비 우선 탐색 BFS
Breadth First Search
처음에 방문한 정점과 인접한 정점들을 차례로 방문
- 먼저 시작점 v를 방문 후 v에 인접한 모든 정점들을 차례로! 방문한다.
- 더 이상 방문할 정점이 없는 경우 다시 v에 인접한 정점 가운데 맨 처음으로 방문한 인접한 정점들을 차례로 방문한다.
- 큐를 사용한다.
시작 정점 : 1 1과 연결된 모든 정점 2,3 큐에 저장 큐에서 2를 꺼내어 1과 연결 2를 시작점으로 방문하지 않은 것 큐에 저장 큐에서 3을 꺼내어 2와 1과 연결 반복 큐가 공백이 되면 연산 종료
동형 그래프
Isomorphic Graph
: 모양은 다르지만 두 그래프가 동일한 정점과 간선으로 이루어져 있는 그래프
- 그래프를 구성하는 정점과 간사이 같다면 다양한 형태의 그래프가 존재할 수 있다.
- 사이클의 길이도 동일하다.
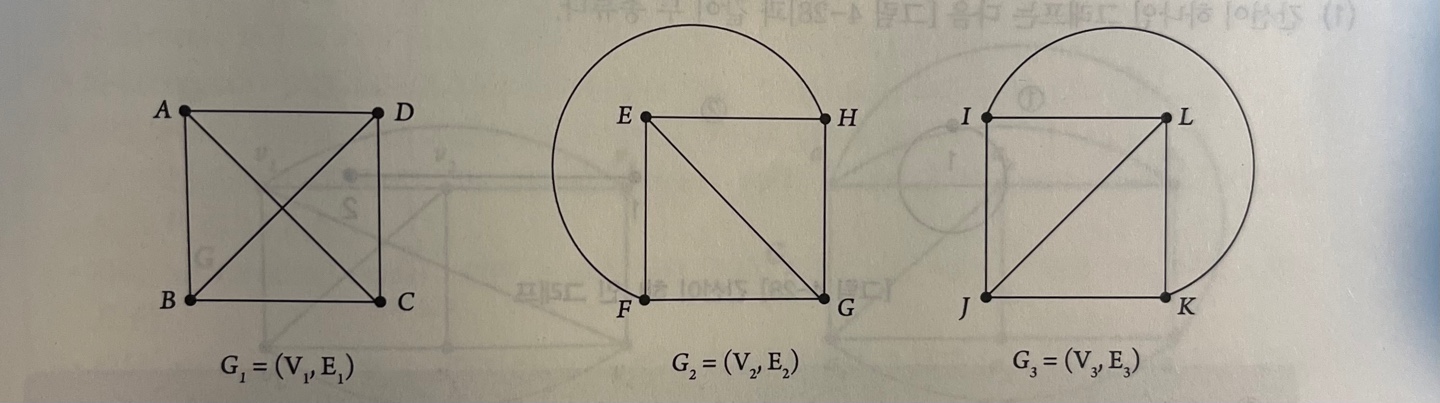
- 각 정점들의 차수를 정리한 후 차수와 같은 값들 사이를 간선으로 고려 대응시키면서 정점들에 대해 다음과 같은 함수 f를 정의할 수 있다.
f : V1 → V2 => f(A) = E, f(B) = F, f(C) = G, f(D) = H f : V1 → V3 => f(A) = I, f(B) = J, f(C) = K, f(D) = L
- 함수 f는 전단사 함수
간선 E에 속하는 임의의 간선을 선택했을 때 그 간선에 대응하는 간선의 쌍이 E2에 존재한다.(A,B) ∈ E 이면 (f(A),f(B)) = (E,F) ∈ E2 이다. (그 역도 성립) 따라서 두 그래프는 서로 동형 그래프이다.
평면 그래프
Planar Graph
: G = <V,E> 를 평면에 그릴 때, 정점이 아닌 곳에서는 어떤 간선도 교차하지 않는 그래프.
면face(면은 평면 그래프에서만 존재)
: 평면 그래프에서 교차하지 않는 간선에 의해 나누어지는 영역
- 평면 그래프는 간선을 경계로 하여 하나 이상의 면으로 구성
(a) : 면이 2개인 평면 그래프 (b), (c) : 면이 1개인 평면 그래프
오일러의 정리 | 오일러의 정리
Euler's Theorem | Formula
: 정점, 간선 면과의 관계를 공식으로 표현한 것.
G = <V,E> 에서 정점의 개수 : |V| = v 간선의 개수 : |E| = e 면의 개수 : s ❗️ 오일러 공식 : v - e + s = 2 정점 개수 - 간선 개수 + 면 개수 = 2이 공식을 증명하기 위해 간선이 하나인 그래프와 간선이 둘 이상인 그래프를 나누어 고려해야함.
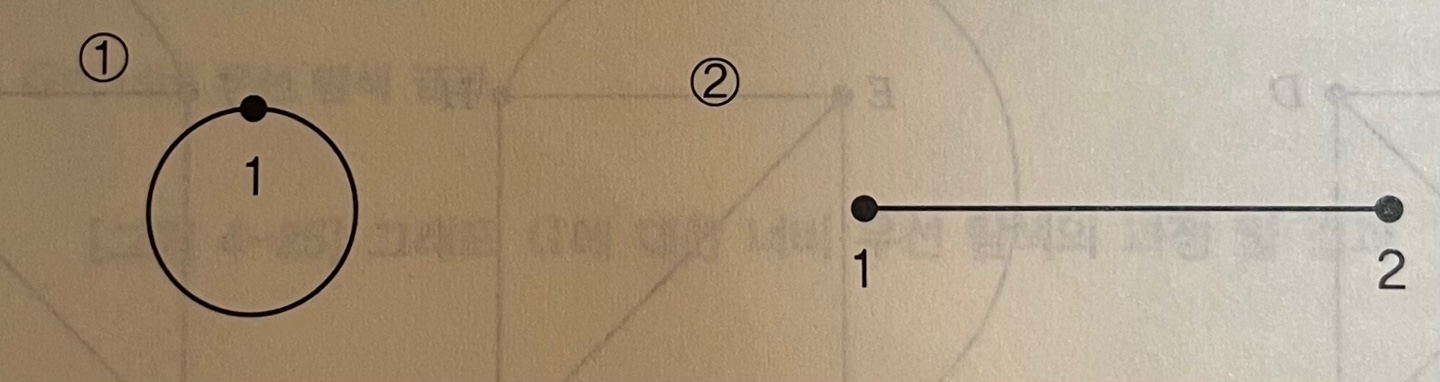
1) 간선이 하나인 그래프
- 즉 변이 하나인 그래프는 이 두 가지가 존재한다.
1) v = 1, e = 1, s = 2 오일러 공식 성립 2) v = 2, e = 1, s = 1 오일러 공식 성립
2) 둘 이상의 간선으로 구성된 그래프
수학적 귀납법을 이용해 증명한다.
1) e = 1 일때 2 - 1 + 1 = 2이므로 오일러 공식이 성립한다. 2) e = k 일 때, v - k + s = 2 로 오일러 공식이 성립한다고 가정 3) e = k + 1 일 때 성립하는지 증명한다.e = k 일 때 그래프에서 간선을 추가해 e = K + 1로 만들어지는 평명 그래프는 두 가지로 나뉜다. 1) 간선 추가를 위해 정점을 추가하는 경우 e = k + 1 / v는 v + 1이 된다. v + 1 - (k + 1) + s = v - k + s 임으로 성립된다. 2) 기존의 정점에 간선을 추가하는 경우 e = k + 1 이지만 정점은 증가하지 않음. 그렇지만 면의 수가 증가한다. s = s + 1 v - (k + 1) + s + 1 = v - k + s 임으로 성립된다.
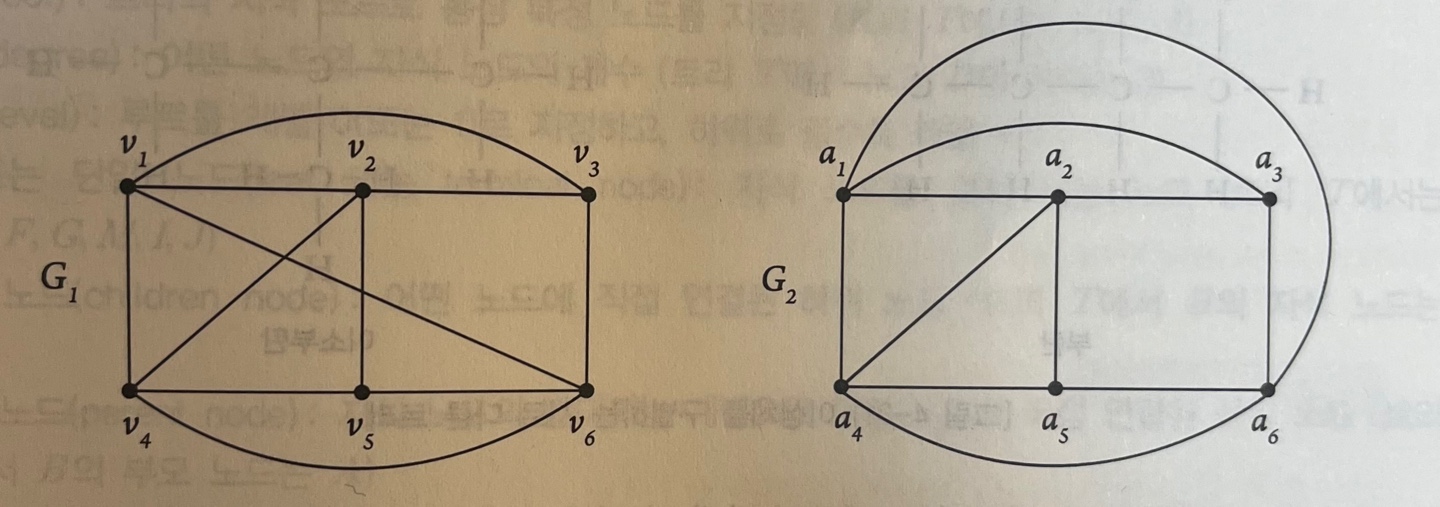
G1은 간선이 교차함으로 평면 그래프가 될 수없어 G2 동형 그래프를 그림. → f(v1) = a1, f(v2) = a2,... 그래프 G1의 정점의 수 = 6 간선의 수 = 11 면의 수를 모른다고 할때 오일러 공식을 사용하면 면의 수는 7개가 된다. 이는 오일러 공식이 성립함을 보여준다.